はじめに
物質の状態図を読み解くことは、その物質の振る舞いを予測するうえでとても重要です。また新しい材料を設計する際も状態図を用いることで、所望の性質や特性を持つ材料の設計が容易となります。状態図(特に合金の状態図)を数値的に計算する方法として、CALPHAD(カルファド)法があります。今回よりCALPHAD法の理解に向けて、状態図計算の基礎について複数回の記事でまとめていきたいと思います。
状態図とは
まず状態図についておさらいしておきます。状態図とはズバリ、「任意の組成・温度・圧力等(状態変数)において、その物質が安定する相や状態(気体、液体、固体など)を図示したもの」です。統計熱力学の分野では相図ともいわれます。
例えば、水の状態図は以下のように書けます。
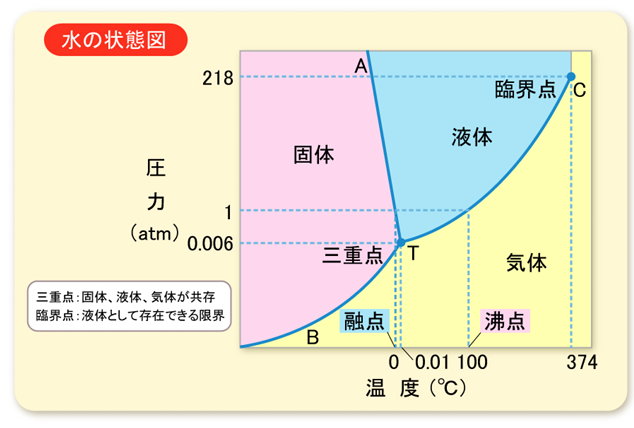
横軸を温度、縦軸を圧力にとり、どの領域で固体・液体・気体になるのかを図示しています。多くの方は昔、化学の教科書で見た記憶があるのではないでしょうか。一般に単一成分系の状態図の場合、軸として温度と圧力が選ばれます。
一方、合金のような多成分系の場合(各元素の組成が変動するような場合)、圧力を一定として組成・温度を軸にとることが慣例です。(もちろん組成を固定値にしたり、3次元にしたりすれば、温度と圧力で書くことも可能です。)例として以下にCr(クロム)とMo(モリブデン)の2成分系の合金状態図を示します。
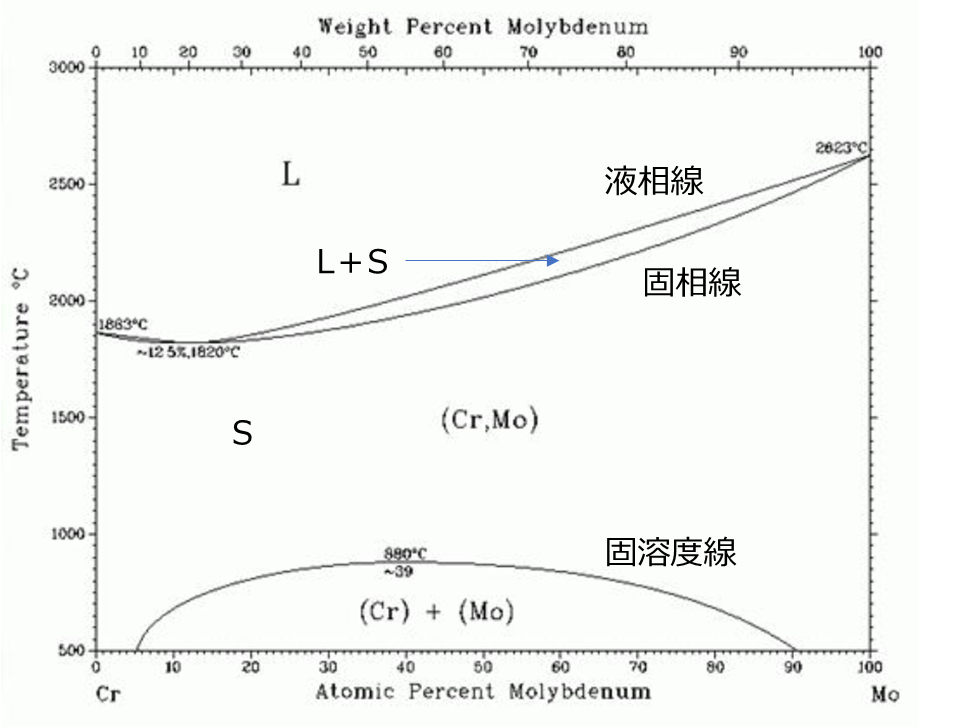
横軸がMoの濃度、縦軸が温度です。またLが液体、Sが固体を示しています。この系では高温で液体、低温では両者が混ざりあった固体(Cr,Mo)、さらに低温では両者が分離した固体((Cr)+(Mo))となっていることが分かります。
これはいわゆる「二相分離状態を持つ全率固溶型」と呼ばれるタイプの状態図です。詳細は省略しますが、状態図は物質ごとの混ざり具合の相性でいくつかのパターンが存在します。(この辺は次回以降で記事にすることにします。)
最後に注意しておきたいのは、状態図はあくまで平衡状態を表したものということです。平衡状態とはある系に変化を与え、その後その系を孤立させ、十分長い時間経過し、その系がそれ以上変化しなくなった状態のことです。したがって、状態図上をたどる変化は平衡状態から平衡状態への変化となり、無限に長い時間をかけてゆっくりと変化させる「準静的過程(=可逆過程)」で行われる必要があります。
一方で実際の系の変化は有限の時間で行われるため、非平衡状態を経由した変化となります。この為、現実では状態図上をたどるような変化は厳密には生じないものと考えられます。このような非平衡状態の取り扱いは非平衡熱力学で記述されます。とはいえ、非平衡状態も十分長い時間がたてば、再び平衡状態に戻りますし、物質の基本的な性質や相遷移の振る舞いを知る上で状態図は欠かせない存在と言えるでしょう。
ギブスの自由エネルギー
では状態図はどのように作成されるのでしょうか?もちろん実験的に確認することはできます。ただ物質の組み合わせは無限にあり、これらを1つずつ実験で求めていくのは大変そうです。そこで出てくるのがCALPHAD法による状態図計算です。
CALPHAD法では各相のギブスの自由エネルギーをモデル化し、その共通接線を見出すことで、数値的に状態図を計算します。
「…なるほど!わからん!」という感じです。恥ずかしながら個人的には「そもそもギブスの自由エネルギーってなんだっけ?」ぐらいの記憶です。そこでまずはギブスの自由エネルギーについておさらいします。ギブスの自由エネルギーは以下のように定義される熱力学における状態変数の1つです。
G=H-TS\tag{1}
\end{align}
ここで\(H\)はエンタルピー、\(T\)は絶対温度、\(S\)はエントロピーです。エンタルピー\(H\)は等圧過程における熱量そのものを意味し、以下の式で定義されます。
H=U+PV\tag{2}
\end{align}
ここで\(U\)は内部エネルギー、\(P\)は圧力、\(V\)は体積です。
さてギブスの自由エネルギー\(G\)の物理的な意味はどういったものだったでしょうか。熱力学の教科書をひっくり返すと以下のように書いてあります。
「ギブスの自由エネルギーは等温・等圧過程において、系から取り出せる非膨張仕事の最大量を示す。」
非膨張仕事とは体積変化を伴わないで行われる仕事のことで、電池のような電気的仕事などが含まれます。例えば等温・等圧過程で何らかの化学反応により系が電気的仕事を行ったとき、ギブスの自由エネルギーは少なくともその値以上に減っているわけです。また以下のような性質もあります。
「等温・等圧過程での自発変化はギブスの自由エネルギー\(G\)が減少する方向に生じる。」
つまり等温・等圧過程であれば、何もしない限りギブスの自由エネルギーが減っていく方向に反応は進むというわけです。そして、その変化がストップした位置が平衡状態ということが出来ます。通常の実験は室温・大気圧で行うわけですから等温・等圧過程というのも自然な制約といえるでしょう。
これを数式で表すと以下のように書けます。
&自発変化の向き:dG<0\tag{4}\\
&平衡条件:dG=0\tag{5}
\end{align}
この辺りはエントロピー増大の法則から導出することが出来ますが、本筋ではないのでとりあえずこの記事では天下り的に扱っておきます。
以下に平衡状態に関する模式図を示します。
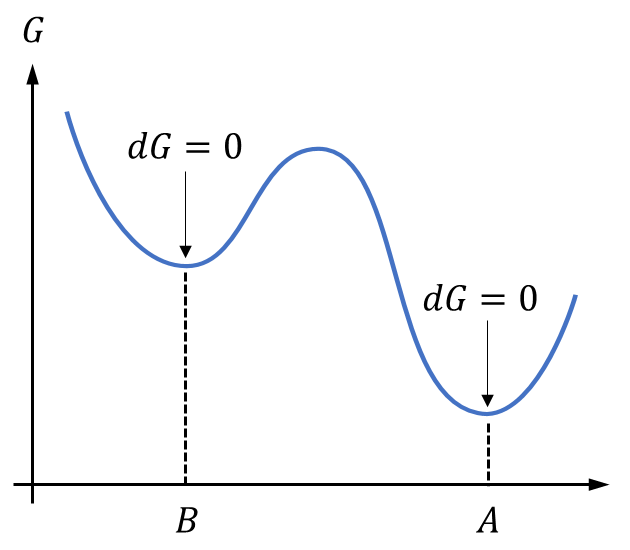
Aの状態は式\((5)\)を満たし、最小の自由エネルギー\(G\)を持つ安定平衡状態と言えます。一方、Bの状態は極小値を示しますが最小の\(G\)ではありません。これを準安定平衡状態と呼びます。両者の中間の\(dG \neq 0\)の状態は不安定状態であり、安定状態に向かおうとします。このとき、相変化が生じます。
式\((1)\)より、より小さな自由エネルギー\(G\)を得るにはエンタルピー\(H\)が小さく、エントロピー\(S\)が大きいことが望ましいことが分かります。したがって低温では内部エネルギー(エンタルピー)の小さい固体が安定となる傾向があります。(強い原子間結合をもつ固体は結合の過程でより多くのエネルギーを放出するため、内部エネルギーが小さくなります。)一方で高温ではエントロピー項(\(-TS\))が支配的になるため、エントロピーが高い、すなわち、より原子が自由に動ける液体や気体が安定となります。
最終的に状態図計算は\(G\)の最小化問題として定式化されることとなります。
化学ポテンシャル
化学ポテンシャルは平衡状態を考える際に重要なパラメーターです。化学ポテンシャルの導入のため、まず多成分からなる固溶体のギブスの自由エネルギ―を考えましょう。
成分1のモル量\(n_{1}\)、成分2のモル量\(n_{2}\)…からなる全モル量\(n\)の固溶体のギブスの自由エネルギーを\(G^{\prime}\)とします。\(G^{\prime}\)は成分\(i\)のモル量\(n_{i}\)および温度\(T\)、圧力\(P\)、その他の環境変数の関数として以下のように書けるものとします。
G^{\prime}=f(n_{1},n_{2},\cdots,T,P,\cdots)\tag{6}
\end{align}
ここで式\((6)\)を全微分して、\(G^{\prime}\)の増分\(dG^{\prime}\)を考えます。
dG^{\prime}=\left(\frac{\partial G^{\prime}}{\partial n_{1}}\right)_{T,P,n_{2},n_{3},\cdots}dn_{1}+\left(\frac{\partial G^{\prime}}{\partial n_{2}}\right)_{T,P,n_{1},n_{3},\cdots}dn_{2}+\cdots\tag{7}
\end{align}
ここでモル量\(n_{i}\)の微分項を以下のように\(\mu_{i}\)と置くこととします。
\mu_{i}=\left(\frac{\partial G^{\prime}}{\partial n_{i}}\right)_{T,P,n_{j}}\qquad j\neq i\tag{8}
\end{align}
\(\mu_{i}\)は「成分\(i\)を微小量増加させる際に生じるギブスの自由エネルギー」を表しており、これを化学ポテンシャルと呼びます。これを用いると式\((6)\)は以下のように書けます。
dG^{\prime}=\mu_{1}dn_{1}+\mu_{2}dn_{2}+\cdots\tag{9}
\end{align}
また\(\mu_{i}\)が成分量\(i\)のモル量\(n_{i}\)に対して一定と仮定すると、上式の両辺を積分することで以下の式が得られます。
G^{\prime}=\mu_{1}n_{1}+\mu_{2}n_{2}+\cdots\tag{10}
\end{align}
上式は\(n\)モルの固溶体の自由エネルギーと化学ポテンシャルの関係を示しています。一般に、任意の量より1モルの固溶体を扱うほうが便利です。そこで両辺を\(n\)モルで割ることとします。
\frac{G^{\prime}}{n}=\mu_{1}\frac{n_{1}}{n}+\mu_{2}\frac{n_{2}}{n}+\cdots\tag{11}
\end{align}
1モル当たりの自由エネルギーを\(G=\frac{G^{\prime}}{n}\)、成分\(i\)のモル分率を\(x_{i}=\frac{n_{i}}{n}\)と書くこととすると、式\((10)\)は次のように書けます。
G=\mu_{1}x_{1}+\mu_{2}x_{2}+\cdots\tag{12}
\end{align}
式\((8)\)についても同様に考えると、1モルの固溶体の自由エネルギーの増分\(dG\)は次のように書けます。
dG=\mu_{1}dx_{1}+\mu_{2}dx_{2}+\cdots\tag{13}
\end{align}
以上が化学ポテンシャルの基本的な定義となります。化学ポテンシャルはある相から微小量の原子を付け加える、または取り除く際のエネルギー変動量を示す物理量であり、異相間での平衡状態の表現・解釈に有用なパラメーターです。この辺は次回の記事でまとめたいと思います。
おわりに
今回は状態図の基本とその計算に必要なギブスの自由エネルギーと化学ポテンシャルについてまとめました。その中でギブスの自由エネルギーの最小化が自発反応の方向性を決めていることが分かりました。次は異相平衡状態におけるギブスの自由エネルギーと化学ポテンシャルについて記載したいと思います。
参考文献
[1] 三浦 憲司ら, “見方・考え方 合金状態図”, オーム社, 2003/11/1



コメント