はじめに
前回記事では、1モル当たりのギブスの自由エネルギー\(G\)は成分(組成)\(i\)のモル分率\(x_{i}\)、化学ポテンシャル\(\mu_{i}\)を用いて以下のように書けました。
G=\mu_{1}x_{1}+\mu_{2}x_{2}+\cdots\tag{1}
\end{align}
これは多成分単一相に関するギブスの自由エネルギーです。例えばある合金が固体状態で安定しているときのギブスの自由エネルギーのみ考えていることに相当します。しかしながら状態図とは異なる相の境界線を示すものなので、状態図を書くには相境界線上でどのようなギブスの自由エネルギーを持つのか知ることが重要です。
例えば、以下の全率固溶型2成分合金の状態図では、赤く示した領域は液体と固体が同時に存在する異相平衡状態にあります。

今回はこのような異相平衡状態でのギブスの自由エネルギーを考えてみましょう。
異相平衡の条件①
例として成分A-Bからなる二元系合金(固溶体)において平衡状態で\(\alpha\)相と\(\beta\)相が共存している異相平衡状態を考えます。このとき合金\(n\)モル当たりのギブスの自由エネルギー\(G’\)は以下のように書けます。
G’={G’}^{\alpha }+{G’}^{\beta }\tag{2}
\end{align}
また平衡状態であるため、前回記事でまとめたギブスの自由エネルギーの平衡条件の式を満たします。
d{G’}=d{G’}^{\alpha}+d{G’}^\beta\tag{3}=0
\end{align}
ここで成分Aを無限少量\(\delta n_{A}\)モルだけ\(\alpha\)相から抜き取って、\(\beta\)相に移した時の変化を考えると、上式は以下のように書けます。
\left(\frac{\partial {G’}^{\alpha}}{\partial n_{A}}\right)_{T,P,n_{B}}\cdot\left(-\delta n_{A}\right)+\left(\frac{\partial {G’}^{\beta}}{\partial n_{A}}\right)_{T,P,n_{B}}\cdot\left(+\delta n_{A}\right)\tag{4}=0
\end{align}
同様に成分Bを無限少量\(\delta n_{B}\)モルだけ\(\alpha\)相から抜き取って、\(\beta\)相に移した時の変化を考えると
\left(\frac{\partial {G’}^{\alpha}}{\partial n_{B}}\right)_{T,P,n_{A}}\cdot\left(-\delta n_{B}\right)+\left(\frac{\partial {G’}^{\beta}}{\partial n_{B}}\right)_{T,P,n_{A}}\cdot\left(+\delta n_{B}\right)\tag{5}=0
\end{align}
以上、式\((4),(5)\)より\(\alpha\)相と\(\beta\)相が平衡する場合の条件式として次式を得ることが出来ます。
\left(\frac{\partial {G’}^{\alpha}}{\partial n_{A}}\right)_{T,P,n_{B}}=\left(\frac{\partial {G’}^{\beta}}{\partial n_{A}}\right)_{T,P,n_{B}}\tag{6}\\
\left(\frac{\partial {G’}^{\alpha}}{\partial n_{B}}\right)_{T,P,n_{A}}=\left(\frac{\partial {G’}^{\beta}}{\partial n_{B}}\right)_{T,P,n_{A}}\tag{7}\\
\end{align}
ここで前回記事より化学ポテンシャルは
\mu_{i}=\left(\frac{\partial G^{\prime}}{\partial n_{i}}\right)_{T,P,n_{j}}\qquad j\neq i\tag{8}
\end{align}
と定義されるので、これを用いると式\((6),(7)\)は次のように書けます。
\mu_{A}^{\alpha}=\mu_{A}^{\beta}\tag{9}\\
\mu_{B}^{\alpha}=\mu_{B}^{\beta}\tag{10}
\end{align}
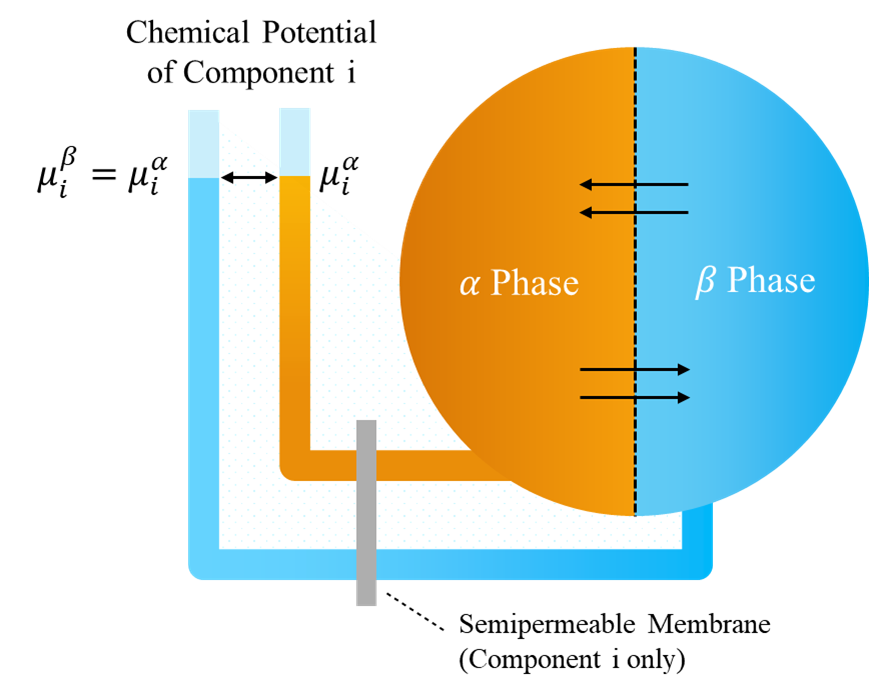
つまり異相平衡状態では「\(\alpha\)相に成分A(B)を微小量付け加える際の化学ポテンシャル\(\mu_{A}^{\alpha}(\mu_{B}^{\alpha})\)」と「\(\beta\)相に成分A(B)を微小量付け加える際の化学ポテンシャル\(\mu_{A}^{\beta}(\mu_{B}^{\beta})\)」が等しくなります。
このことは次のように考えることが出来ます。平衡状態は系全体のギブスの自由エネルギーを最小化するように実現するのでした(式\((3)\))。例えば\(\mu_{A}^{\alpha}>\mu_{A}^{\beta}\)あれば、成分Aは\(\alpha\)相いると余分な自由エネルギーが生じてしまうので、\(\beta\)相へ移動したほうが安定です。逆に\(\mu_{A}^{\alpha}<\mu_{A}^{\beta}\)であれば、\(\alpha\)相が安定となります。
このような理屈で系全体の自由エネルギーが最小となるため、成分AとBの間の移動は、それぞれの成分の化学ポテンシャルが各相間で等しくなるまで続きます。これは以下の図のようにピトー管中の水が圧力によって、同じ高さまで到達することに類似しています。
異相平衡の条件②
次にギブスの自由エネルギーと化学ポテンシャルの関係をより明確にするため、\(\alpha\)相と\(\beta\)相からなる異相平衡状態のうち、特に\(\alpha\)相に注目して議論を進めます。
今、モル分率\(x_{A}(=1-x_{B})\)の成分Aとモル分率\(x_{B}\)の成分Bよりなる\(\alpha\)相1モル当たりの自由エネルギーを\(G^{\alpha}(x_{A},x_{B})\)とします。また、モル数\(n_{A}\)の成分Aとモル数\(n_{B}\)の成分Bよりなる\(\alpha\)相\((n_{A}+n_{B})\)モルの全自由エネルギーを\(G’^{\alpha}(n_{A},n_{B})\)と置きます。すると一般にギブスの自由エネルギーは物質量に比例する示量変数なので、\(G^{\alpha}(x_{A},x_{B})\)と\(G’^{\alpha}(n_{A},n_{B})\)の間には以下の関係式が成り立ちます。
&G’^{\alpha}(n_{A},n_{B})=(n_{A}+n_{B})G^{\alpha}(x_{A},x_{B})\\
&\rightarrow
G’^{\alpha}(n_{A},n_{B})=(n_{A}+n_{B})G^{\alpha}(1-x_{B},x_{B})\tag{11}\\
\end{align}
ここで上式を化学ポテンシャルの定義式\((8)\)と結びつけるため、式\((11)\)の両辺を\(n_{A}\)で偏微分します。積の微分公式を使うと
&\left(\frac{\partial G’^{\alpha}}{\partial n_{A}}\right)_{T,P,n_{B}}=G^{\alpha}+(n_{A}+n_{B})\left(\frac{\partial G^{\alpha}(1-x_{B},x_{B})}{\partial x_{B}}\right)_{T,P}\left(\frac{\partial x_{B}}{\partial n_{A}}\right)_{T,P,n_{B}}\tag{12}\\
\end{align}
左辺は\(\alpha\)相に成分Aを微小量付け加える際の化学ポテンシャル\(\mu_{A}^{\alpha}\)そのものなので、以下のように書けます。
\mu_{A}^{\alpha}=G^{\alpha}+(n_{A}+n_{B})\left(\frac{\partial G^{\alpha}(1-x_{B},x_{B})}{\partial x_{B}}\right)_{T,P}\left(\frac{\partial x_{B}}{\partial n_{A}}\right)_{T,P,n_{B}}\tag{13}\\
\end{align}
右辺第二項の微分項の取り扱いに一瞬戸惑いますが、\(x_{A},x_{B}\)はモル分率を表すので、全モル数\(n_{A},n_{B}\)との間には以下の式が成り立つはずです。
x_{A} =\frac{n_{A}}{n_{A}+n_{B}} \tag{14}\\
x_{B} =\frac{n_{B}}{n_{A}+n_{B}} \tag{15}\\
\end{align}
したがって、式\((13)\)の右辺に現れる微分項\(\left(\frac{\partial x_{B}}{\partial n_{A}}\right)_{T,P,n_{B}}\)は商の微分公式を用いて以下のように書けます。
\left(\frac{\partial x_{B}}{\partial n_{A}}\right)_{T,P,n_{B}}=\frac{-n_{B}}{(n_{A}+n_{B})^2}=\frac{-x_{B}}{n_{A}+n_{B}} \tag{16}\\
\end{align}
これを式\((13)\)に再び代入すると以下の式が得られます。
\mu_{A}^{\alpha}=G^{\alpha}-x_{B}\left(\frac{\partial G^{\alpha}}{\partial x_{B}}\right)_{T,P}\tag{17}\\
\end{align}
また\(\mu_{B}^{\alpha}\)についても、ここまでの方法と同様に式\((11)\)の両辺を\(n_{B}\)で偏微分することで以下のように書けます。
\mu_{B}^{\alpha}=G^{\alpha}+(1-x_{B})\left(\frac{\partial G^{\alpha}}{\partial x_{B}}\right)_{T,P}\tag{18}\\
\end{align}
次回以降の記事でまとめる予定ですが、1モル当たりのギブスの自由エネルギー\(G^{\alpha}\)は一般の合金では各成分のモル分率\(x_{A},x_{B}\)に対して、下に凸の曲線として与えられることが知られています。下に凸ということは純金属でいるより、合金状態でいるほうが安定であることを示しています。(上に凸の合金はギブスの自由エネルギー最小化の観点から基本的には生じ得ない。)
例えば、式\((17),(18)\)は以下のようにグラフ化することが出来ます。
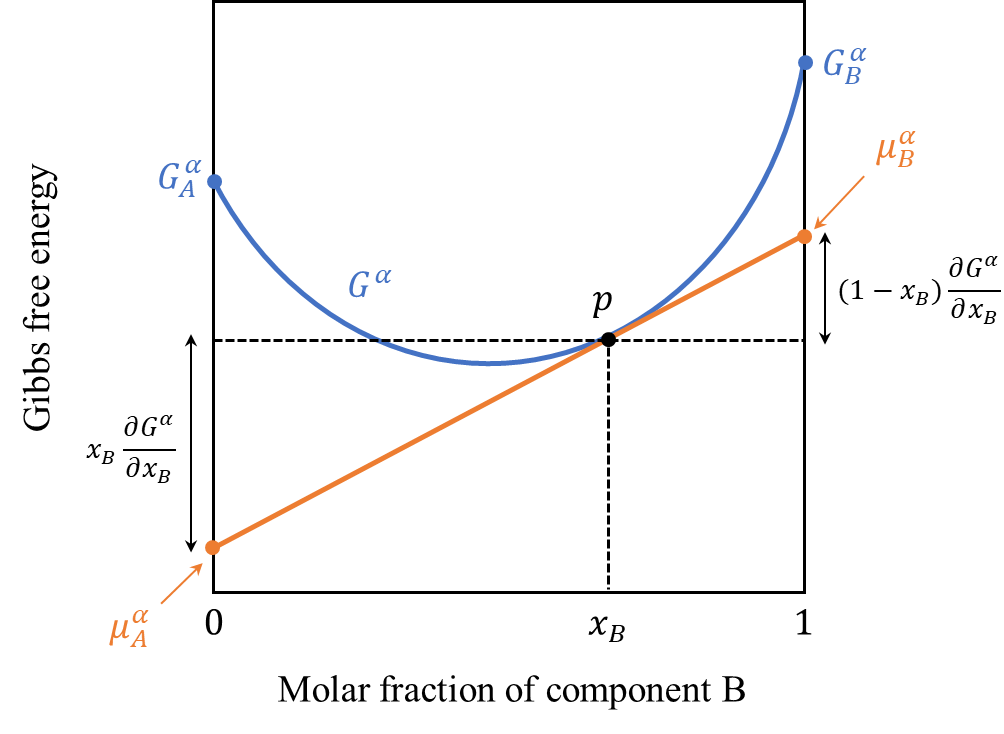
組成\(x_{B}\)において1モル当たりのギブスの自由エネルギー\(G^{\alpha}\)の接線を引き、\(x_{B}=0\)の軸との交点が\(\mu_{A}^{\alpha}\)、\(x_{B}=1\)の軸との交点が\(\mu_{B}^{\alpha}\)に相当します。
このグラフは示唆に富んでいて、ギブスの自由エネルギーと化学ポテンシャルについていくつかの関係性を示しています。
例えば上のグラフでは\(\mu_{A}^{\alpha}<\mu_{B}^{\alpha}\)となっており、成分Bより成分Aを付け加えるエネルギーのほうが少ない状態です。一方で濃度が\(x_{B}’\)となった下のグラフの場合、逆に\(\mu_{A}^{\alpha}>\mu_{B}^{\alpha}\)となっており、成分Aより成分Bを付け加えるエネルギーのほうが少ない状態です。このことは組成的には\(\mu_{A}^{\alpha}=\mu_{B}^{\alpha}\)となる\(dG=0\)の極値が最も安定な状態であることを示しています。
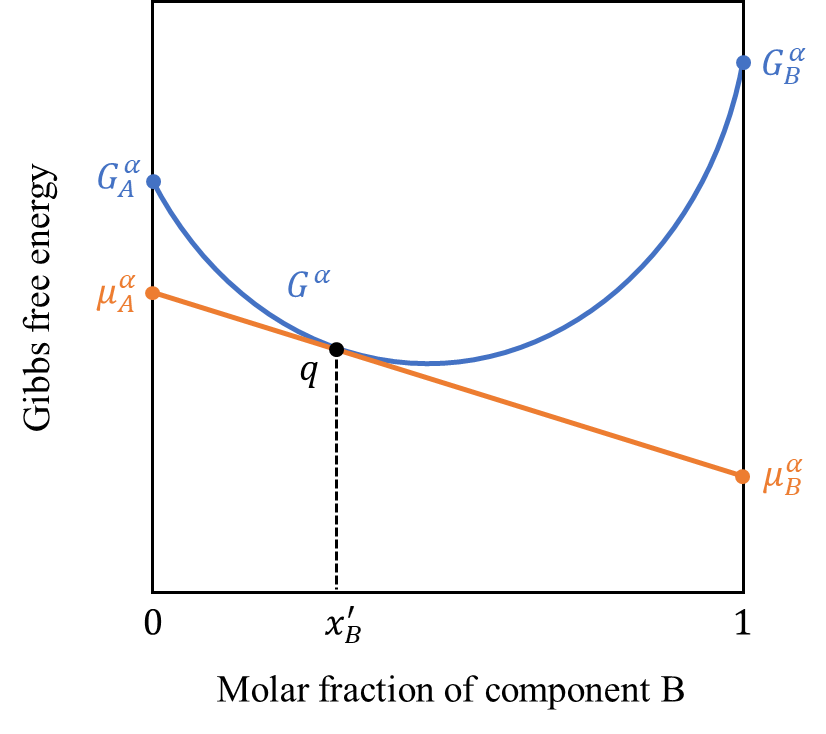
また固溶体状態(\(0<x_{B}<1\))では「純金属1モルのギブスの自由エネルギー\(G_{A}^{\alpha}、G_{B}^{\alpha}\)」より「化学ポテンシャル\(\mu_{A}^{\alpha}、\mu_{B}^{\alpha}\)」のほうが常に小さく、\(x_{B}=0\)または\(x_{B}=1\)に近づくにつれて、両者が一致していくことが分かります。
前回記事でまとめた通り、化学ポテンシャルとは近似的に「その成分1モル当たりのギブスの自由エネルギー」と考えることが出来るのでした(式\((1)\))。したがって、「固溶体中の金属Aの1モル当たりの自由エネルギー」より「純金属Aの1モル当たりの自由エネルギー」のほうが大きく、固溶体のほうが純金属より安定であることを示しています。
共通接線の法則
ここまでは\(\alpha\)相と\(\beta\)相からなる異相平衡状態の\(\alpha\)相のみに注目して議論を進めてきましたが、ここからは\(\alpha\)相と\(\beta\)相の関係性について考えていきます。
今、下図のように\(\alpha\)相と\(\beta\)相がそれぞれ下に凸のギブスの自由エネルギーを持つとします。この時、各モル分率でどのような相状態が実現されるでしょうか?系としてはギブスのエネルギーを最小化する相が実現されるので、二つの曲線の交点のモル分率を\(x_{p}\)とおくと、一見、\(0\sim x_{p}\)では\(\alpha\)相、\(x_{p}\sim 1\)では\(\beta\)相が実現しそうな気がします。ただ、実際はこれほどシンプルではありません。

ここで異相平衡条件の式\((9),(10)\)を再掲します。異相平衡状態では各相の化学ポテンシャルが等しくなるのでした。
\mu_{A}^{\alpha}=\mu_{A}^{\beta}\tag{9}\\
\mu_{B}^{\alpha}=\mu_{B}^{\beta}\tag{10}
\end{align}
また前節より各相の化学ポテンシャルは自由エネルギー曲線の接線と\(x_{B}=0,1\)軸の交点として現れるのでした。したがって、異相平衡条件を満たすモル分率\(x_{B}^{\alpha},x_{B}^{\beta}\)は曲線\(G^{\alpha},G^{\beta}\)の共通接線を形成する点であること分かります。

したがって、実際は\(0\sim x_{B}^{\alpha}\)で\(\alpha\)相、\(x_{B}^{\alpha}\sim x_{B}^{\beta}\)で\(\alpha + \beta\)相、\(x_{B}^{\beta}\sim 1\)で\(\beta\)相が実現します。単一相の間に\(\alpha\)相と\(\beta\)相が共存する異相平衡状態が存在するわけです。このように2つの相の自由エネルギー曲線に共通の接線を引ける場合には、接点の組成において両相が互いに平衡することを意味します。これを「共通接線の法則」と呼びます。
より具体的に考えます。例えば下図のように成分Bのモル分率\(x_{p}\)が\(x_{B}^{\alpha}\)と\(x_{B}^{\alpha}\)の間にある場合を考えます。
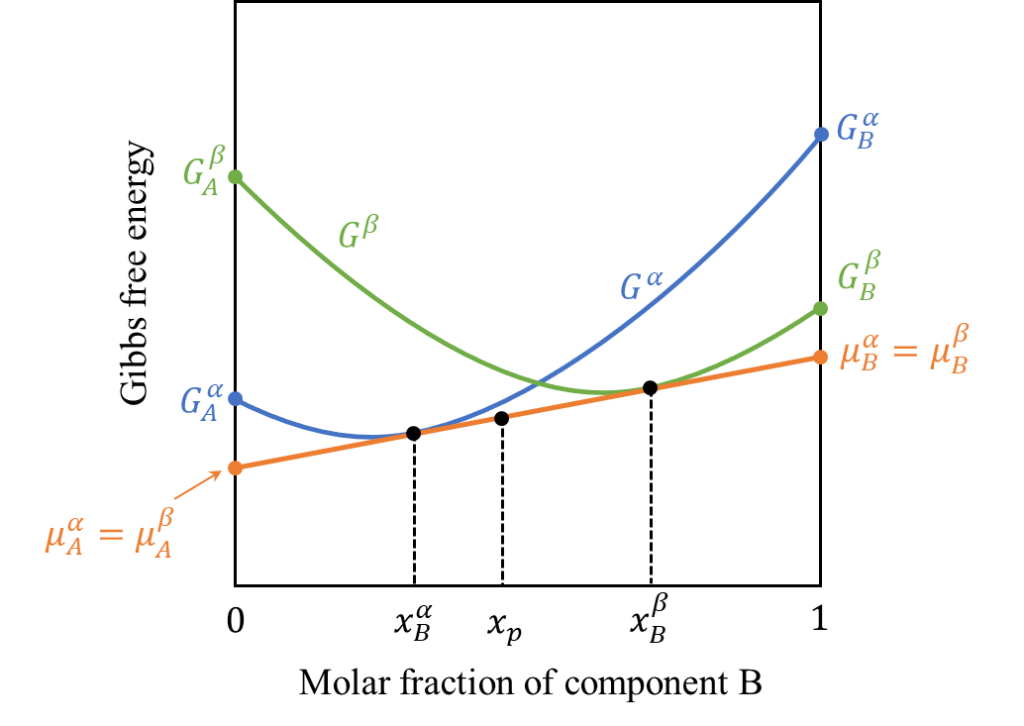
この時、一見、モル分率\(x_{p}\)の\(\alpha\)相が現れるように思いますが、実際はモル分率\(\frac{x_{B}^{\beta}-x_{p}}{x_{B}^{\beta}-x_{B}^{\alpha}}\cdot x_{p}\)の\(\alpha\)相とモル分率\(\frac{x_{p}-x_{B}^{\alpha}}{x_{B}^{\beta}-x_{B}^{\alpha}}\cdot x_{p}\)の\(\beta\)相が共存している状態となります。これら二つのモル分率は足し合わせると\(x_{p}\)となり、成分Bに関する合計のモル分率に変化はありません。
すなわち\(x_{p}\)で線分\(x_{B}^{\alpha}x_{B}^{\beta}\)を逆比に内分したモル分率で各相が実現します。このような規則を「天秤の法則(Lever Rule)」と呼びます。以下に上記の模式図を示します。単一の\(\alpha\)相よりも\(\alpha\)相と\(\beta\)相の共存状態のほうがギブスの自由エネルギーが小さくなっており、より安定している状態であることが分かります。
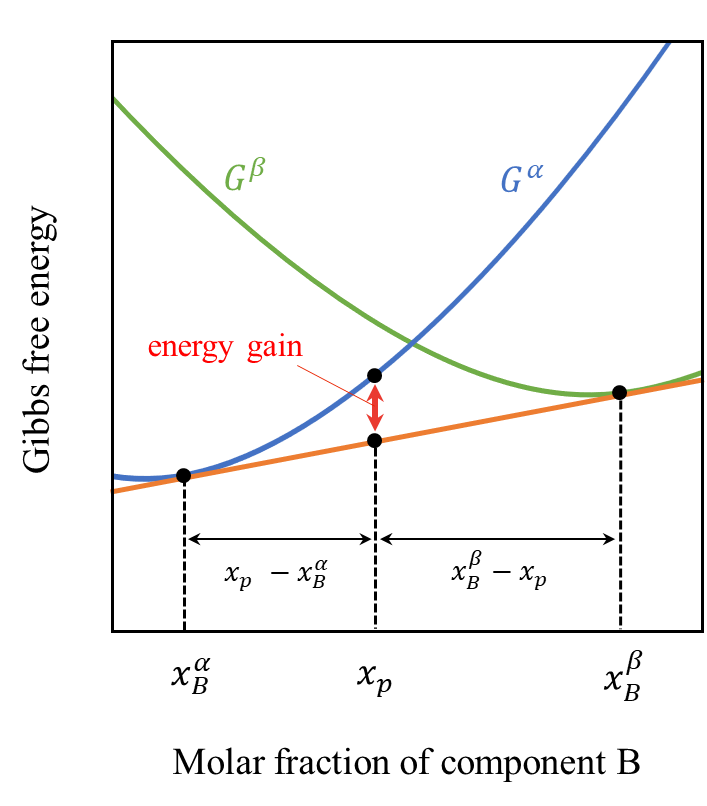
上記のように異相平衡状態では自由ネエネルギー曲線の共通接線を見出すことで、どのような相状態が実現するか把握することが出来ます。これが状態図計算の第一歩です。
おわりに
今回は異相平衡状態におけるギブスの自由エネルギーと化学ポテンシャルについてまとめました。状態図は自由エネルギー曲線の共通接線から描ける点がポイントです。これを数値的に行うことが出来れば状態図計算が可能になるはずです(多分…)。カルファド法にいつたどり着けるのか道は見えていませんが、今後も気ままにまとめていこうと思います。では。
参考文献
[1] 三浦 憲司ら, “見方・考え方 合金状態図”, オーム社, 2003/11/1
[2] 須藤 一ら, “金属組織学 (金属工学標準教科書)”, 丸善, 1972/8/1



コメント