はじめに
唐突ですが合金の状態図は見たことがありますか?理系の方の多くは一度はどこかで見たことがあるのではないでしょうか。例えば最もシンプルな状態図の一つであるAg(銀)-Pd(パラジウム)の2元系合金の状態図は以下のようなものです。
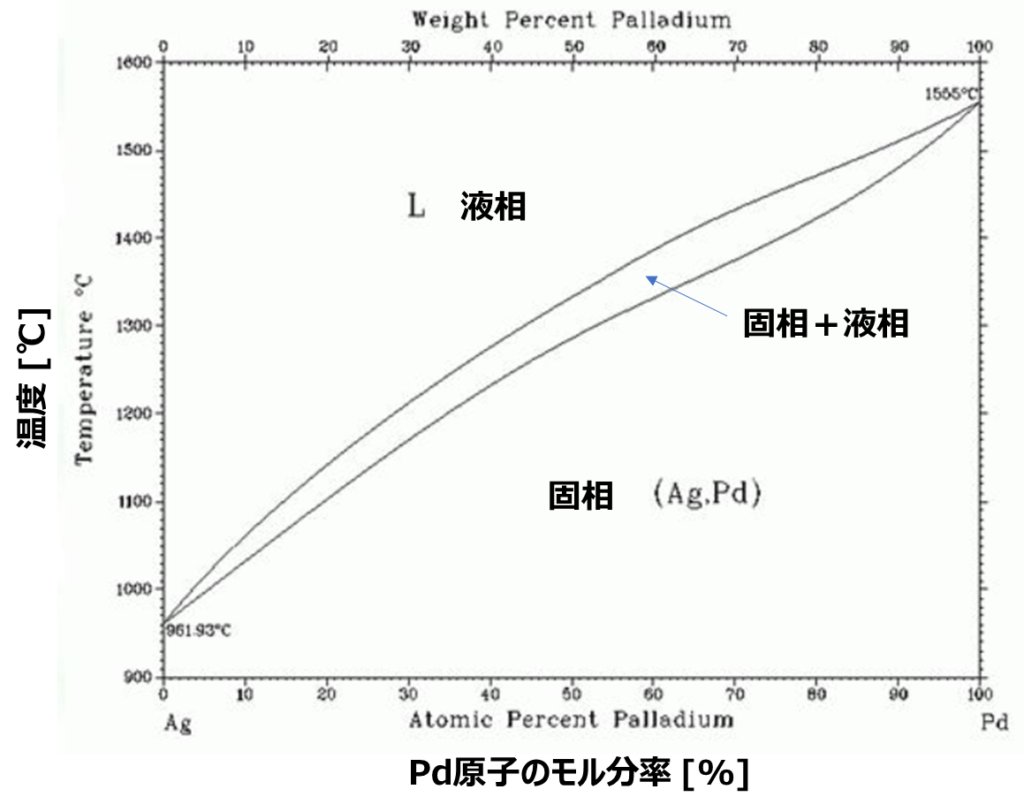
縦軸は温度、横軸がPdのモル分率を示しており、その時の合金の取り得る相状態が記載されています。高温側には液相、低温側には固相の領域が広がっており、その間に両者が共存する異相平衡状態が見られます。
このように状態図とは「任意の組成-温度においてその合金がどんな相状態を取るのかを示した図」と言えます。状態図はその合金の特性を理解したり、材料設計を行う際に非常に有意義な情報を提供してくれるので、材料工学の分野では欠かせない存在です。
ではこの状態図、いったいどうやって求めるのでしょうか?もちろん実験で求めることは可能です。ただ金属はたくさん種類がありますし、その組み合わせである合金となると膨大なパターンが存在します。いちいち実験をしてたのでは大変です。
そこで今回は状態図を数値計算から求める方法、CALPHAD(CALculation of PHAse Diagrams)法についてご紹介します。CALPHAD法は1970年代にスウェーデン王立工科大学にて開発され、今日に至るまで様々な合金設計に用いられてきました。
本記事ではオープンソースなどに頼らず、単純な系で実際にCALPHAD法を実装してみてそのエッセンスをつかみます。私自身も勉強中の身ではありますが、CALPHAD法の入り口を実感していてもらえると嬉しいです。
なお、本記事はMATLAB/Simulink Advent Calendar 2023への参加記事です。CALPHAD法の最適化計算にはMATLAB本体とOptimization Toolboxを利用しています。
CALPHAD法
CALPHAD法では、各相のギブスの自由エネルギー曲線の共通接線を求めることで相と相の間にある異相平衡状態を見つけ出し、状態図を作成していきます。
簡単な例として二種の金属原子A、Bからなり、固相(\(\alpha\)相)および液相を持つA-B2元系合金を考えます。このとき、\(\alpha\)相と液相のギブスの自由エネルギー\(G^{\alpha},G^{L}\)は以下のように与えられます。
G^{\alpha}= &G_{A}^\alpha \left(1- x_{B}\right)+G_{B}^\alpha x_{B}+\Omega_{AB}^{\alpha} (1-x_{B})x_{B} +RT\left[(1-x_{B})\log{(1-x_{B})}+x_{B}\log{x_{B}}\right]\tag{1}\\
G^{L}= &\left(G_{A}^\alpha +RT_{A}\right)\left(1- x_{B}\right)+\left(G_{B}^\alpha+RT_{B}\right) x_{B}+\Omega_{AB}^{L} (1-x_{B})x_{B} \\
&+RT\left[(1-x_{B})\log{(1-x_{B})}+x_{B}\log{x_{B}}\right]-RT\tag{2}
\end{align}
各変数の意味は以下の通りです。
| 変数名 | 意味 |
|---|---|
| \(x_{B}\) | 金属原子Bのモル分率 |
| \(T\) | 合金の温度 |
| \(G_{A}^\alpha\) | \(T[K]\)における純金属Aの1モル当たりのギブスの自由エネルギー |
| \(G_{B}^\alpha\) | \(T[K]\)における純金属Bの1モル当たりのギブスの自由エネルギー |
| \(\Omega_{AB}^{\alpha}\) | \(T[K]\)における固溶体の金属A、Bの結合によるギブスの自由エネルギー |
| \(\Omega_{AB}^{L}\) | \(T[K]\)における液体の金属A、Bの結合によるギブスの自由エネルギー |
| \(T_{A}\) | 金属Aの融点 |
| \(T_{B}\) | 金属Bの融点 |
| \(R\) | 気体定数:1.987[cal/mol deg] |
上記の導出に関して興味がある方は次の記事をご参考ください。
ここで、各組成におけるギブスの自由エネルギーについて\(G_{A}^\alpha (1-x_{B})+G_{B}^\alpha x_{B}\)を基準点とすることで、以下のように式\((1),(2)\)をさらにシンプルな形にしておきます。
\Delta G^{\alpha}= &\Omega_{AB}^{\alpha} (1-x_{B})x_{B} +RT\left[(1-x_{B})\log{(1-x_{B})}+x_{B}\log{x_{B}}\right]\tag{3}\\
\Delta G^{L}=& RT_{A}\left(1- x_{B}\right)+RT_{B} x_{B}+\Omega_{AB}^{L} (1-x_{B})x_{B}
\\
&+RT\left[(1-x_{B})\log{(1-x_{B})}+x_{B}\log{x_{B}}\right]-RT\tag{4}
\end{align}
CALPHAD法では上式の\(\Delta G^{\alpha},\Delta G^{L}\)を原子Bのモル分率 \(x_{B}\)についてプロットし、その共通接線を求めます。以下に一例として、\(\Delta G^{\alpha},\Delta G^{L}\)の共通接線を引いた例を記載します。

この共通接線の接点\(x_1,x_{2}\)について、温度ごとにプロットしていくことで状態図を得ることが出来ます。何故これが状態図となるのか詳しく知りたい方は次の記事をご参考ください。
共通接線探索
次に共通接線の求め方について考えます。共通接線は以下の1次式で与えられるものとします。
y=ax+b\tag{5}
\end{align}
この時、共通接線の傾き\(a\)と\(\Delta G^{\alpha},\Delta G^{L}\)の間には以下の式が成り立ちます。
&\Delta G^{\alpha\prime}(x_{1})= a\tag{6}\\
&\Delta G^{L\prime}(x_{2})=a\tag{7}
\end{align}
ここで\(\Delta G^{\alpha\prime},\Delta G^{L\prime}\)は\(\Delta G^{\alpha},\Delta G^{L}\)の\(x_{B}\)に関する一回微分を表し、式\((3),(4)\)より具体的には以下のように書けます。
&\Delta G^{\alpha\prime}(x_{B})= \Omega_{AB}^{\alpha} (1-2x_{B}) +RT \log{\frac{x_{B}}{1-x_{B}}}\tag{8}\\
&\Delta G^{L\prime}(x_{B})= \Omega_{AB}^{L} (1-2x_{B}) +RT \log{\frac{x_{B}}{1-x_{B}}}-R(T_{A}-T_{B})\tag{9}
\end{align}
式\((6),(7)\)は位置\(x_{1},x_{2}\)で共通接線をなすとき、共通接線の傾き\(a\)と位置\(x_{1},x_{2}\)におけるそれぞれのギブスの自由エネルギー曲線の傾き\(\Delta G^{\alpha\prime}(x_{1}),\Delta G^{L\prime}(x_{2})\)が一致することを示しています。
さらに\(x_{1},x_{2}\)を用いると共通接線の傾き\(a\)および切片\(b\)は以下のように書けます。
&a=\frac{\Delta G^{\alpha}(x_{1})-\Delta G^{L}(x_{2})}{x_{1}-x_{2}}\tag{10}\\
&b=\Delta G^{\alpha}(x_{1})-ax_{1}=\Delta G^{\alpha}(x_{1})-\frac{\Delta G^{\alpha}(x_{1})-\Delta G^{L}(x_{2})}{x_{1}-x_{2}}x_{1}
\tag{11}\end{align}
したがって、式\((10)\)より式\((6),(7)\)は以下のように書けます。
&\Delta G^{\alpha\prime}(x_{1})= \frac{\Delta G^{\alpha}(x_{1})-\Delta G^{L}(x_{2})}{x_{1}-x_{2}}\tag{12}\\
&\Delta G^{L\prime}(x_{2})=\frac{\Delta G^{\alpha}(x_{1})-\Delta G^{L}(x_{2})}{x_{1}-x_{2}}\tag{13}
\end{align}
このような条件を満たす\(x_{1},x_{2}\)を見つけることが出来れば、式\((10),(11)\)から共通接線を構築することが出来ます。
今回、\(x_{1},x_{2}\)の探索には逐次二次計画法(SQP)を利用します。逐次二次計画法は非線形最適化のための反復解法の一つでMATLAB上では「fmincon」関数で利用することが出来ます。
探索する設計変数は以下の範囲を満たす\(x_{1},x_{2}\)の二つになります。
0<x_{1}<1\tag{14}\\
0<x_{2}<1\tag{15}\\
\end{align}
また目的関数は、式\((12),(13)\)の和として以下のように考えます。
minimize\left[abs\left(\Delta G^{\alpha\prime}(x_{1})- \frac{\Delta G^{\alpha}(x_{1})-\Delta G^{L}(x_{2})}{x_{1}-x_{2}}\right)+abs\left(\Delta G^{L\prime}(x_{2})-\frac{\Delta G^{\alpha}(x_{1})-\Delta G^{L}(x_{2})}{x_{1}-x_{2}}\right)\right]\tag{16}
\end{align}
以上、式\((14)\sim(16)\)について逐次二次計画法で最適化を行い、共通接線を求めることで状態図を作成します。
全率可溶型状態図
ここからは具体的な計算結果を紹介します。まずは全率可溶型状態図です。全率可溶型はどの組成でも完全に固溶体を形成する最もシンプルなタイプの状態図です。冒頭で述べたAg-Pd2元系合金もこのタイプに属します。
全率可溶型を実現するギブスの自由エネルギーのパラメーターとしては以下が挙げられます。
| 変数名 | 値 |
|---|---|
| \(\Omega_{AB}^{\alpha}\) | 0[cal/mol deg] |
| \(\Omega_{AB}^{L}\) | 0[cal/mol deg] |
| \(T_{A}\) | 900[K] |
| \(T_{B}\) | 300[K] |
| \(R\) | 気体定数:1.987[cal/mol deg] |
二種の原子の結合によるエントロピー\(\Omega_{AB}^{\alpha},\Omega_{AB}^{L}\)が0となるのが特徴です。これは二つの原子の間には特別な相互作用は働かず、無秩序かつ完全に混ざり合った状態であることを意味しています。
以下に計算結果を示します。左側はモル分率とギブスの自由エネルギーの関係を示したグラフ、右側は共通接線の接点を温度ごとにプロットしたグラフ、すなわち状態図です。
比較のため、Ag-Pd2元系合金の状態図も再掲します。

両者を比較すると状態図が液相線と固相線で構成されるという特徴が一致しています。
溶解度ギャップを持つ状態図
次はもう少し複雑な溶解度ギャップを持つ状態図にチャレンジします。溶解度ギャップとは、2種の金属が完全に混ざり合わず、液相または固相に分離する組成範囲のことを指します。以下に例として、Cr-Mo系の二元系合金の状態図を示します。
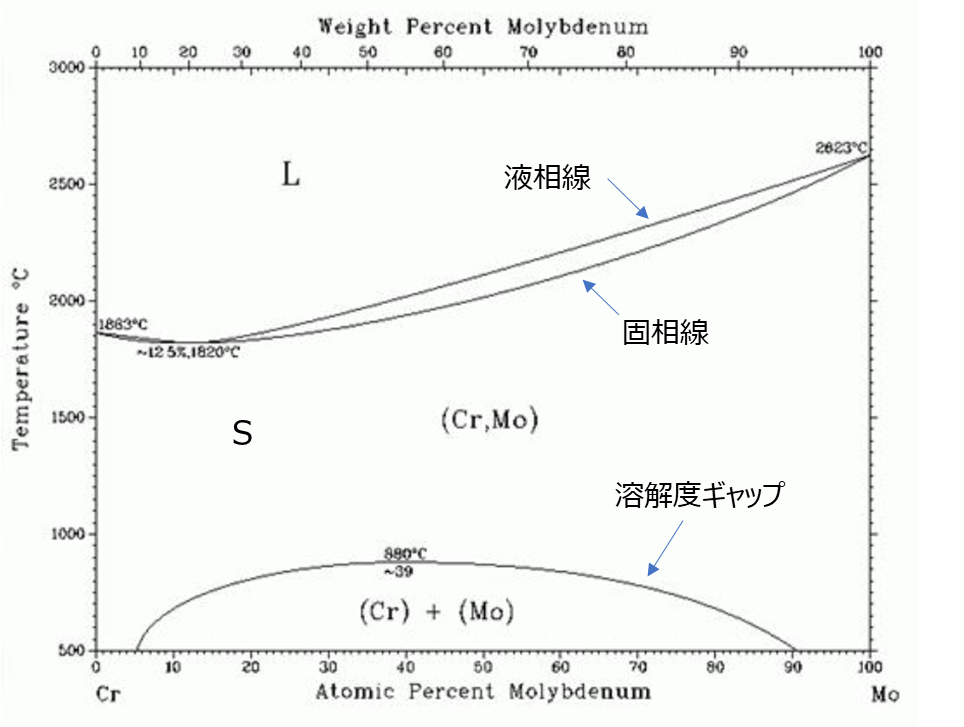
下側に溶解度ギャップの領域が生じ、全率可溶型の状態図を比較しても少し複雑な形となっています。このような状態図を実現するギブスの自由エネルギーのパラメーターとしては以下が挙げられます。
| 変数名 | 値 |
|---|---|
| \(\Omega_{AB}^{\alpha}\) | 2000[cal/mol deg] |
| \(\Omega_{AB}^{L}\) | 0[cal/mol deg] |
| \(T_{A}\) | 900[K] |
| \(T_{B}\) | 300[K] |
| \(R\) | 気体定数:1.987[cal/mol deg] |
固相(\(\alpha\)相)における二種の原子の結合によるエントロピー\(\Omega_{AB}^{\alpha}\)が正の値となるのが特徴です。これは固相状態において原子A,Bの間に斥力が働くことを示しています。
ここで注意したいのは、全率可溶型の場合は液相と固相の自由エネルギー曲線の共通接線を探索しましたが、溶解度ギャップを持つ場合、これに加えて固相の自由エネルギー曲線内の共通接線も探索する必要があります。
したがって二種の最適化を行う必要があり、目的関数として以下が加わります。
minimize\left[abs\left(\Delta G^{\alpha\prime}(x_{1})- \frac{\Delta G^{\alpha}(x_{1})-\Delta G^{\alpha}(x_{2})}{x_{1}-x_{2}}\right)+abs\left(\Delta G^{\alpha\prime}(x_{2})-\frac{\Delta G^{\alpha}(x_{1})-\Delta G^{\alpha}(x_{2})}{x_{1}-x_{2}}\right)\right]\tag{17}
\end{align}
このような条件の下、最適化した結果を以下に示します。
上の動画より\(\alpha\)相の自由エネルギー曲線内で共通接線を探索することで、溶解度ギャップが再現されていることが分かります。
以上が計算結果の紹介になります。状態図はこれら以外にもさまざま複雑な形が存在しますが、基本的には上記のようなアプローチで作成することが出来ます。
MATLABコード
以下に今回用いたMATLABコードを記載します。
%% 初期化処理
clc; close all;
clear all;
%% パラメーター設定
dxB = 0.001;
xB = 0.0001 : dxB : 0.9999; % B原子のモル分率
T = 200 : 5 : 1600; % 計算温度範囲
omega_alpha = 2000; % α相の原子間相互作用パラメーター
omega_L = 0; % 液相の原子間相互作用パラメーター
R = 1.987; % 気体定数[cal/mol deg]
TA = 900; % 原子Aの融点
TB = 1300; % 原子Bの融点
% 変数宣言
dG_max = 0; % ギブスの自由エネルギー曲線の最大値。可視化範囲決定用。
dG_min = 0; % ギブスの自由エネルギー曲線の最小値。可視化範囲決定用。
xmat = []; % 最適化結果格納用の変数
xmat_Equilibrium = []; % 最適化結果格納用の変数(安定平衡線のみ)
xmat_QuasiEquilibrium = []; % 最適化結果格納用の変数(準安定平衡線のみ)
%% 最適化による共通接線探索
% /////////////////////////////////////////
% pflag : 共通接線を探索する自由エネルギー曲線を選択するフラグ
% pflag = 1 : α相と液相の間の共通接線を求める
% pflag = 2 : α相内の共通接線を求める
% pflag = 3 : 液相内の共通接線を求める
% /////////////////////////////////////////
% α相と液相の間の共通接線を求める
pflag = 1;
num_trials = 50; % 異なる初期値で最適化を実行する回数
[xmat, dG_max, dG_min] = ...
Calphad_optmodule(xB, T, R, TA, TB, omega_alpha, omega_L, xmat, dG_max, dG_min, pflag, num_trials);
% α相内の共通接線を求める
pflag = 2;
num_trials = 50; % 異なる初期値で最適化を実行する回数
[xmat, dG_max, dG_min] = ...
Calphad_optmodule(xB, T, R, TA, TB, omega_alpha, omega_L, xmat, dG_max, dG_min, pflag, num_trials);
% 液相内の共通接線を求める
pflag = 3;
num_trials = 50; % 異なる初期値で最適化を実行する回数
[xmat, dG_max, dG_min] = ...
Calphad_optmodule(xB, T, R, TA, TB, omega_alpha, omega_L, xmat, dG_max, dG_min, pflag, num_trials);
%% 可視化
% 可視化用のマトリクスxmat2を構築。
% 解が見つからなかった温度をNanで埋める。
xmat2 = [];
for j = 1 : length(T)
t = T(j);
% xmat の中で該当する温度の行を見つける
rows = xmat(xmat(:, 1) == t, :);
if isempty(rows)
% 対応する行がない場合、NaN を使用して温度のみを追加
xmat2 = [xmat2; t, NaN, NaN, NaN]; % NaNを追加する列数はxmatの列数に合わせる
else
% 対応する全ての行を追加
xmat2 = [xmat2; rows];
end
end
% 安定平衡線と準安定平衡線の分離計算
for i = 1 : size(xmat2, 1)
[xmat_Equilibrium, xmat_QuasiEquilibrium] ...
= SeparateQuasiEquilibrium(xmat2, xB, R, omega_alpha, omega_L, TA, TB, ...
dG_max, dG_min, i, T, xmat_Equilibrium, xmat_QuasiEquilibrium);
end
% 動画保存
for i = 1 : size(xmat2, 1)
if i == 1
figure(2);
set(gcf, 'Position', [100, 100, 1200, 600]); % ウィンドウサイズを設定
% plotconfig(xmat, xB, R, omega_alpha, omega_L, TA, TB, dG_max, dG_min, i, T)
plotconfig(xmat_Equilibrium, xB, R, omega_alpha, omega_L, TA, TB, dG_max, dG_min, i, T)
filename = ['omega_alpha = ', num2str(omega_alpha, '%.0f'), ', omega_L = ', num2str(omega_L, '%.0f'), '.mp4'];
v = VideoWriter(filename,'MPEG-4');
v.FrameRate = 20;
open(v);
else
% plotconfig(xmat, xB, R, omega_alpha, omega_L, TA, TB, dG_max, dG_min, i, T)
plotconfig(xmat_Equilibrium, xB, R, omega_alpha, omega_L, TA, TB, dG_max, dG_min, i, T)
frame = getframe(gcf);
writeVideo(v,frame);
end
end
close(v);% 動画ファイルを閉じる
%% 以下ローカル関数
% /////////////////////////////////////////
% 可視化設定
% /////////////////////////////////////////
function [] = plotconfig(xmat, xB, R, omega_alpha, omega_L, TA, TB, dG_max, dG_min, i, T)
% 最適化結果から必要な情報を取り出す
Tx = xmat(i, 1);
x1 = xmat(i, 2);
x2 = xmat(i, 3);
pflag = xmat(i, 4);
if pflag == 1 || isnan(pflag)% α相と液相の共通接線の場合、または共通接線を持たない場合。
% 共通接線の構築
c0 = (CalcGibssAlpha(omega_alpha, x1, R, Tx) - CalcGibssLiquid(R, TA, x2, TB, omega_L, Tx))/(x1 - x2);
c1 = CalcGibssAlpha(omega_alpha, x1, R, Tx) - c0 * x1;
yc = c0 .* xB + c1;
% 各相のギブスの自由エネルギーの計算
dG_Alpha = CalcGibssAlpha(omega_alpha, xB, R, Tx);
dG_L = CalcGibssLiquid(R, TA, xB, TB, omega_L, Tx);
% 共通接線の描画
subplot(1,2,1)
plot(xB, dG_Alpha, xB, dG_L, xB, yc); hold on
plot(x1, CalcGibssAlpha(omega_alpha, x1, R, Tx), 'ro')
plot(x2, CalcGibssLiquid(R, TA, x2, TB, omega_L, Tx), 'bo')
elseif pflag == 2 % α相内の共通接線の場合
% 共通接線の構築
c0 = (CalcGibssAlpha(omega_alpha, x1, R, Tx) - CalcGibssAlpha(omega_alpha, x2, R, Tx))/(x1 - x2);
c1 = CalcGibssAlpha(omega_alpha, x1, R, Tx) - c0 * x1;
yc = c0 .* xB + c1;
% 各相のギブスの自由エネルギーの計算
dG_Alpha = CalcGibssAlpha(omega_alpha, xB, R, Tx);
dG_L = CalcGibssLiquid(R, TA, xB, TB, omega_L, Tx);
% 共通接線の描画
subplot(1,2,1)
plot(xB, dG_Alpha, xB, dG_L, xB, yc); hold on
plot(x1, CalcGibssAlpha(omega_alpha, x1, R, Tx), 'ro')
plot(x2, CalcGibssAlpha(omega_alpha, x2, R, Tx), 'bo')
elseif pflag == 3 % 液相内の共通接線の場合
% 共通接線の構築
c0 = (CalcGibssLiquid(R, TA, x1, TB, omega_L, Tx)- CalcGibssLiquid(R, TA, x2, TB, omega_L, Tx))/(x1 - x2);
c1 = CalcGibssLiquid(R, TA, x1, TB, omega_L, Tx) - c0 * x1;
yc = c0 .* xB + c1;
% 各相のギブスの自由エネルギーの計算
dG_Alpha = CalcGibssAlpha(omega_alpha, xB, R, Tx);
dG_L = CalcGibssLiquid(R, TA, xB, TB, omega_L, Tx);
% 共通接線の描画
subplot(1,2,1)
plot(xB, dG_Alpha, xB, dG_L, xB, yc); hold on
plot(x1, CalcGibssLiquid(R, TA, x1, TB, omega_L, Tx), 'ro')
plot(x2, CalcGibssLiquid(R, TA, x2, TB, omega_L, Tx), 'bo')
end
% グラフオプション
title(['temperature = ', num2str(Tx, '%.0f'), ' [K]']);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 12);
%axis equal;
axis tight;
axis on;
fig=gcf;
fig.Color='white';
xlim([0 1])
deltaG = dG_max - dG_min;
ylim([dG_min - deltaG / 10 dG_max + deltaG / 10])
xlabel('x_B')
ylabel('Gibbs free energy')
legend('Galpha','Gliquid','Common Tangent','FontSize', 10)
% 新しいプロットの時、軸設定を保持したまま前のグラフィックスオブジェクトを消去
set(gca,'nextplot','replacechildren');
% 相図の描画
subplot(1,2,2)
red_points = xmat(1 : i, 2); % 赤い点のx座標
blue_points = xmat(1 : i, 3); % 青い点のx座標
temperatures = xmat(1 : i, 1); % 温度
% 赤い点と青い点をプロット
plot(red_points, temperatures, 'r.'); hold on;
plot(blue_points, temperatures, 'b.');
% グラフオプション
xlim([0 1])
ylim([200 1400])
ylim([min(T) - 50 max(T) + 50])
xlabel('x_B')
ylabel('temperature[K]')
title(['temperature = ', num2str(Tx, '%.0f'), ' [K]']);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 12);
% 新しいプロットの時、軸設定を保持したまま前のグラフィックスオブジェクトを消去
set(gca,'nextplot','replacechildren');
end
% /////////////////////////////////////////
% 目的関数の定義
% /////////////////////////////////////////
function y = obj_fit(x, omega_alpha, R, T, TA, TB,omega_L,pflag)
if pflag == 1
% α相と液相の間の共通接線を求める目的関数を設定する
c0 = (CalcGibssAlpha(omega_alpha, x(1), R, T) - CalcGibssLiquid(R, TA, x(2), TB, omega_L, T))/(x(1) - x(2));
dG_Alpha_prime = CalcGibssAlphaPrime(omega_alpha, x(1), R, T);
dG_L_prime = CalcGibssLiquidPrime(R, TA, x(2), TB, omega_L, T);
y = abs(dG_Alpha_prime - c0) + abs(dG_L_prime - c0); % 目的関数
elseif pflag == 2
% α相内の共通接線を求める目的関数を設定する
c0 = (CalcGibssAlpha(omega_alpha, x(1), R, T) - CalcGibssAlpha(omega_alpha, x(2), R, T))/(x(1) - x(2));
dG_Alpha_prime1 = CalcGibssAlphaPrime(omega_alpha, x(1), R, T);
dG_Alpha_prime2 = CalcGibssAlphaPrime(omega_alpha, x(2), R, T);
y = abs(dG_Alpha_prime1 - c0) + abs(dG_Alpha_prime2 - c0); % 目的関数
%x(1) と x(2) の差が minDiff 未満の場合にペナルティを適用
penaltyFactor = CalcPenaltyFactor(x);
y = y + penaltyFactor;
elseif pflag == 3
% 液相内の共通接線を求める目的関数を設定する
c0 = (CalcGibssLiquid(R, TA, x(1), TB, omega_L, T) - CalcGibssLiquid(R, TA, x(2), TB, omega_L, T))/(x(1) - x(2));
dG_L_prime1 = CalcGibssLiquidPrime(R, TA, x(1), TB, omega_L, T);
dG_L_prime2 = CalcGibssLiquidPrime(R, TA, x(2), TB, omega_L, T);
y = abs(dG_L_prime1 - c0) + abs(dG_L_prime2 - c0); % 目的関数
%x(1) と x(2) の差が minDiff 未満の場合にペナルティを適用
penaltyFactor = CalcPenaltyFactor(x);
y = y + penaltyFactor;
end
end
% /////////////////////////////////////////
% α相のギブスの自由エネルギー
% /////////////////////////////////////////
function dG_alpha = CalcGibssAlpha(omega_alpha, xB, R, T)
dG_alpha = omega_alpha * (1 - xB) .* xB + R * T * ((1 - xB) .* log(1 - xB) + xB .* log(xB));
end
% /////////////////////////////////////////
% 液相のギブスの自由エネルギー
% /////////////////////////////////////////
function dG_L = CalcGibssLiquid(R, Ta, xB, Tb, omega_L, T)
dG_L = R * Ta * (1 - xB) + R * Tb * xB + omega_L * (1 - xB) .* xB - R * T ...
+ R * T * ((1 - xB) .* log(1 - xB) + xB .* log(xB));
end
% /////////////////////////////////////////
% α相のギブスの自由エネルギーの一階微分
% /////////////////////////////////////////
function dG_alpha_p = CalcGibssAlphaPrime(omega_alpha, xB, R, T)
dG_alpha_p = omega_alpha * (1 - 2 .* xB) + R * T * log(xB./(1 - xB));
end
% /////////////////////////////////////////
% 液相のギブスの自由エネルギーの一階微分
% /////////////////////////////////////////
function dG_L_p = CalcGibssLiquidPrime(R, Ta, xB, Tb, omega_L, T)
dG_L_p = - R * (Ta - Tb) + omega_L * (1 - 2 .* xB) + R * T * log(xB./(1 - xB));
end
% /////////////////////////////////////////
% 最適化による共通接線の探索
% /////////////////////////////////////////
function [xmat, dG_max, dG_min] =...
Calphad_optmodule(xB, T, R, TA, TB,omega_alpha, omega_L, xmat, dG_max, dG_min, pflag, num_trials)
% 最適化パラメーター
nvars = 2; % 変数の数
LB = [0.001 0.001]; % 下限
UB = [0.999 0.999]; % 上限
solutions = zeros(num_trials, nvars); % 最適解を保存する配列
fvals = zeros(num_trials, 1); % 目的関数値を保存する配列
% 線形制約(なし)
A = [];
b = [];
Aeq = [];
beq = [];
% 非線形制約(なし)
nonlcon = [];
% 最適化オプションの設定。アルゴリズムは逐次二次計画法(sqp)を選択。
%options = optimoptions('fmincon', 'Algorithm', 'sqp', 'Display', 'off');
options = optimoptions('fmincon', 'Algorithm', 'sqp', 'Display', 'off', ...
'TolFun', 1e-6, 'TolX', 1e-6, 'MaxIter', 10000);
% 温度毎に共通接線を探索
for i = 1 : size(T, 2)
% 進行度の出力
disp([num2str(T(i)),'[K]/',num2str(T(end)), '[K]を計算中です。']);
% 可視化範囲決定用に最大値と最小値を求める
dG_max = max([CalcGibssAlpha(omega_alpha, xB, R, T(i)) ...
CalcGibssLiquid(R, TA, xB, TB, omega_L, T(i)) dG_max]) ;
dG_min = min([CalcGibssAlpha(omega_alpha, xB, R, T(i)) ...
CalcGibssLiquid(R, TA, xB, TB, omega_L, T(i)), dG_min]) ;
% 目的関関数の設定
ObjFunc = @(x) obj_fit(x, omega_alpha, R, T(i), TA, TB, omega_L, pflag);
% 初期値の設定(ラテン超方格)
[samplingPoints] = CreateInitialPoint(num_trials);
% 初期値を変更し最適化を実行
for j = 1 : num_trials
% 初期値
% x = [rand(1, 2)]; % 2変数の場合、それぞれの値は 0 から 1 の範囲でランダムに選ばれる
x = [samplingPoints(j, :)]; % 2変数の場合、それぞれの値は 0 から 1 の範囲でランダムに選ばれる
% 最適化の実行
[x, fval] = fmincon(ObjFunc, x, A, b, Aeq, beq, LB, UB, nonlcon, options);
% 結果の保存
%fval
solutions(j, :) = x;
fvals(j,:) = fval;
end
% 目的関数の値が1より大きい解は消去する。
threshold = 1; % 閾値の設定
evalmat = [solutions fvals];
evalmat(evalmat(:, nvars + 1) > threshold, :) = [];
solutions = evalmat(:, 1 : 2);
fvals = evalmat(:, 3);
% 同じ相の自由エネルギー曲線の中で、共通接線の探索を行う場合(pflag=2,3)、
% 成分が入れ替わっただけの解を見分けるため、昇順に並べ替える。
% 各行の1列目と2列目を比較し、小さい方を1行目に、大きい方を2行目に移動する。
if pflag == 2 || pflag == 3
for l = 1:size(solutions, 1)
solutions(l, 1:2) = sort(solutions(l, 1:2));
end
end
% 最適化結果の評価
if size(evalmat, 1) == 0
disp('失敗。共通接線が見つかりませんでした。');
else
disp('成功。共通接線が見つかりました。');
% クラスタリングで類似した解を一つにまとめる。
epsilon = 0.01; % 近傍の半径
MinPts = 1; % クラスタを形成するために必要な最小点数
idx = dbscan(solutions, epsilon, MinPts);% クラスタリング(DBSCAN)の実行
% クラスタリング結果の表示
%disp('クラスタリング結果:');
%disp(idx);
% 各クラスタの中心を求める
unique_clusters = unique(idx);
cluster_centers = zeros(length(unique_clusters) - 1, size(solutions, 2)); % -1 to exclude noise
for k = 1 : length(unique_clusters)
if unique_clusters(k) ~= -1 % ノイズでない場合
cluster_centers(k, :) = mean(solutions(idx == unique_clusters(k), :), 1);
end
end
disp('クラスタ中心:');
disp(cluster_centers);
% 求めた最適値を保存
Tvec = T(i) * ones(size(cluster_centers,1),1);
pflagvec = pflag * ones(size(cluster_centers,1),1);
xtemp = [Tvec cluster_centers pflagvec] ;
xmat = cat(1, xmat, xtemp);% ここまでの最適値の結果に加える
end
end
end
% /////////////////////////////////////////
% ペナルティの計算
% /////////////////////////////////////////
function penaltyFactor = CalcPenaltyFactor(x)
minDiff = 0.05; % x(1)とx(2)の最小差異
if abs(x(1) - x(2)) < minDiff
penaltyFactor = 10^16; % ペナルティの大きさ
else
penaltyFactor = 0;
end
end
% /////////////////////////////////////////
% 安定平衡線と準安定平衡線の分離計算
% /////////////////////////////////////////
function [xmat_Equilibrium, xmat_QuasiEquilibrium] ...
= SeparateQuasiEquilibrium(xmat, xB, R, omega_alpha, omega_L, TA, TB, ...
dG_max, dG_min, i, T, xmat_Equilibrium, xmat_QuasiEquilibrium)
% 最適化結果から必要な情報を取り出す
Tx = xmat(i, 1);
x1 = xmat(i, 2);
x2 = xmat(i, 3);
pflag = xmat(i, 4);
if pflag == 1 || isnan(pflag)% α相と液相の共通接線の場合、または共通接線を持たない場合。
% 共通接線の構築
c0 = (CalcGibssAlpha(omega_alpha, x1, R, Tx) - CalcGibssLiquid(R, TA, x2, TB, omega_L, Tx))/(x1 - x2);
c1 = CalcGibssAlpha(omega_alpha, x1, R, Tx) - c0 * x1;
yc = c0 .* xB + c1;
% 各相のギブスの自由エネルギーの計算
dG_Alpha = CalcGibssAlpha(omega_alpha, xB, R, Tx);
dG_L = CalcGibssLiquid(R, TA, xB, TB, omega_L, Tx);
elseif pflag == 2 % α相内の共通接線の場合
% 共通接線の構築
c0 = (CalcGibssAlpha(omega_alpha, x1, R, Tx) - CalcGibssAlpha(omega_alpha, x2, R, Tx))/(x1 - x2);
c1 = CalcGibssAlpha(omega_alpha, x1, R, Tx) - c0 * x1;
yc = c0 .* xB + c1;
% 各相のギブスの自由エネルギーの計算
dG_Alpha = CalcGibssAlpha(omega_alpha, xB, R, Tx);
dG_L = CalcGibssLiquid(R, TA, xB, TB, omega_L, Tx);
elseif pflag == 3 % 液相内の共通接線の場合
% 共通接線の構築
c0 = (CalcGibssLiquid(R, TA, x1, TB, omega_L, Tx)- CalcGibssLiquid(R, TA, x2, TB, omega_L, Tx))/(x1 - x2);
c1 = CalcGibssLiquid(R, TA, x1, TB, omega_L, Tx) - c0 * x1;
yc = c0 .* xB + c1;
% 各相のギブスの自由エネルギーの計算
dG_Alpha = CalcGibssAlpha(omega_alpha, xB, R, Tx);
dG_L = CalcGibssLiquid(R, TA, xB, TB, omega_L, Tx);
end
% 求めた共通接線が各相のギブスの自由エネルギーよりも小さいかを確認する。
dEmax = max([max(yc - dG_Alpha) max(yc - dG_L)]);
% エネルギーの大小によって配列を振り分ける
if dEmax > 0
xmat_QuasiEquilibrium(i, :) = xmat(i, :);
xmat_Equilibrium(i, :) = [Tx, NaN, NaN, NaN];
elseif dEmax <= 0
xmat_Equilibrium(i, :) = xmat(i, :);
xmat_QuasiEquilibrium(i, :) = [Tx, NaN, NaN, NaN];
else
xmat_Equilibrium(i, :) = [Tx, NaN, NaN, NaN];
xmat_QuasiEquilibrium(i, :) = [Tx, NaN, NaN, NaN];
end
end
% /////////////////////////////////////////
% ラテン超方格法による初期値生成
% /////////////////////////////////////////
function [samplingPoints] = CreateInitialPoint(numPoints)
% 任意の範囲を設定
rangeX = [0.001, 0.999];
rangeY = [0.001, 0.999];
% 2次元のラテン超方格サンプリングを生成
lhsMatrix = lhsdesign(numPoints, 2);
% 範囲に合わせてスケーリング
xPoints = rangeX(1) + (rangeX(2) - rangeX(1)) * lhsMatrix(:, 1);
yPoints = rangeY(1) + (rangeY(2) - rangeY(1)) * lhsMatrix(:, 2);
% XとYが同じになる点を除外し、新しい点を追加
tolerance = 1e-6; % 同一と見なすための許容誤差
i = 1;
while i <= length(xPoints)
if abs(xPoints(i) - yPoints(i)) < tolerance
% 新しい点を追加
newX = rangeX(1) + (rangeX(2) - rangeX(1)) * rand();
newY = rangeY(1) + (rangeY(2) - rangeY(1)) * rand();
if abs(newX - newY) >= tolerance
xPoints(i) = newX;
yPoints(i) = newY;
else
continue; % 新しい点が条件を満たさない場合はスキップ
end
end
i = i + 1;
end
% 点を組み合わせて一つの行列にする
samplingPoints = [xPoints, yPoints];
% % 行列を表示
% disp(samplingPoints);
%
% % 点をプロット
% scatter(samplingPoints(:, 1), samplingPoints(:, 2));
% title(['', num2str(numPoints), '点のラテン超方格サンプリング(X ≠ Y)']);
% xlabel('X軸');
% ylabel('Y軸');
end
おわりに
本記事では状態図を数値的に求めるCALPHAD法について紹介しました。CALPHAD法を理解することで、今までなんとなく見ていた状態図の本質をより深く理解することが出来るようになります。また、共通接線を数値的に求めていく独特な問題設定は他分野では見られない面白い考え方です。
今回は最も単純な2元系合金を対象としましたが、実際の合金は10を超える金属から構成されることも多く、共通接線(接面)の探索はより複雑なものとなると考えられます。しかしエッセンスは変わらないので、2元系の考え方から派生的に展開できるはずです。本記事を通してCALPHAD法の入り口を体験してもらえたら何よりです。
参考文献
[1] 三浦 憲司ら, “見方・考え方 合金状態図”, オーム社, 2003/11/1
[2] 須藤 一ら, “金属組織学 (金属工学標準教科書)”, 丸善, 1972/8/1
[3] 長谷部 光弘ら, “最近の状態図に関する研究“, 日本金属学会会報/11 巻 (1972) 12 号



コメント