はじめに
前回記事では以下のアレンカーン方程式の導出を行いました。
\frac{\partial \phi}{\partial t}&=-M_{\phi}\frac{\delta G}{\delta \phi} \tag{1}\\
G(\phi, \nabla\phi,\nabla ^2\phi)&=\int_V g(\phi, \nabla\phi,\nabla ^2\phi)dV\tag{2}
\end{align}
上式を解くにはギブスの自由エネルギーの空間密度\(g\)の中身を明確にする必要があります。そこで今回は\(g\)の具体的な定式化についてまとめたいと思います。
ギブスの自由エネルギーのモデル化
天下りではありますが、以下に最終的に得られるエネルギーの空間密度\(g\)の式を示します。
g&=g_{chem}+g_{doub}+g_{grad}\tag{3}\\
g_{chem}&=p(\phi)g_{a}+(1-p(\phi))g_{b}\tag{4}\\
g_{doub}&=Wq(\phi)\tag{5}\\
g_{grad}&=\frac{a^2}{2}(\nabla \phi)^2\tag{6}\\
\end{align}
ここで\(g_{chem}\)は化学的自由エネルギー密度、\(g_{doub}\)はダブルウェルポテンシャル、\(g_{grad}\)は勾配エネルギー密度を示します。次から各項がどんな意味を持つのか順に確認していきます。
化学的自由エネルギー密度\(g_{chem}\)
化学的自由エネルギー密度\(g_{chem}\)は組織がバルク状態で持つ、原子間の結合エネルギーや熱的な振動エネルギーなどを表します。
今、単純な系としてa相、b相の2つの相からなる組織状態を考えます。例えばa相は液体、b相は固体と考えればよいでしょう。この時、これらの相の界面移動速度\(V\rm[m/s]\)は次式で与えられます。
V= M\Delta g =M\left(g_a-g_b\right) \tag{7}
\end{align}
ここで\(M\)は界面モビリティ\(\rm{[m^4/J\cdot s]}\)、\(g_a,g_b\)はそれぞれの相が持つ化学的自由エネルギー密度\(\rm{[J/m^3]}\)を表します。また、相間の化学的自由エネルギー密度の差分\(\Delta g=g_a-g_b\)は界面移動速度\(V\)を決めるため、化学的駆動力と呼ばれます。
相界面は\(\Delta g\)の符号に応じて、化学的自由エネルギー密度が低い相から高い相に向かって移動します。また、平衡状態においては\(\Delta g = 0\)となり移動が停止します。
各相の化学的自由エネルギー密度\(g_a,g_b\)を用いると、任意の相状態の化学的自由エネルギー密度\(g_{chem}\)は次式で与えられます。
g_{chem}= p(\phi)g_{a}+(1-p(\phi))g_{b} \tag{8}
\end{align}
ここで\(p(\phi)\)はエネルギー密度分布関数と呼ばれ、具体的には
p(\phi)=\phi ^2(3-2\phi) \tag{9}
\end{align}
もしくは
p(\phi)=\phi ^3(10-15\phi+6\phi ^2) \tag{10}
\end{align}
などが広く用いられます。
式\((9),(10)\)をグラフ化すると次のようになります。
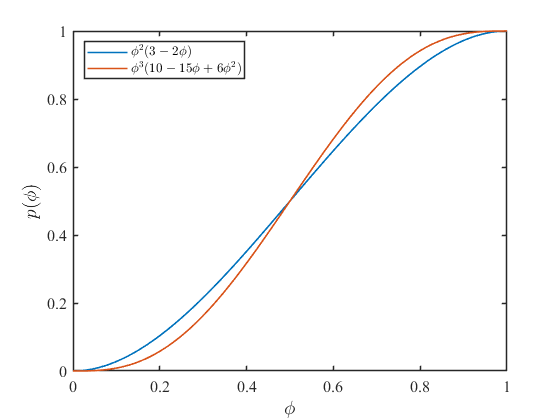
エネルギー密度分布関数\( p(\phi)\)は\(p(0) = 0,p(1) = 1\)を取り、その間が\(p'(0) =p'(1) = 0\)の曲線で滑らかにつながれています。
したがって式\((8)\)より、組織がb相（\(\phi = 0\)）の時は\(g_{chem}=g_{b}\)、組織がa相（\(\phi = 1\)）の時は\(g_{chem}=g_{a}\)、その間の時は\(p(\phi),(1-p(\phi))\)を重みとして、連続的に変化します。
このように二つの相の間のエネルギー変化を滑らかにとることで数値的な安定性を得ることが出来ます。
例えば、\(g_a=1, g_b=3\)の時、式\((8),(9)\)より\(g_{chem}\)は次のようなグラフになります。
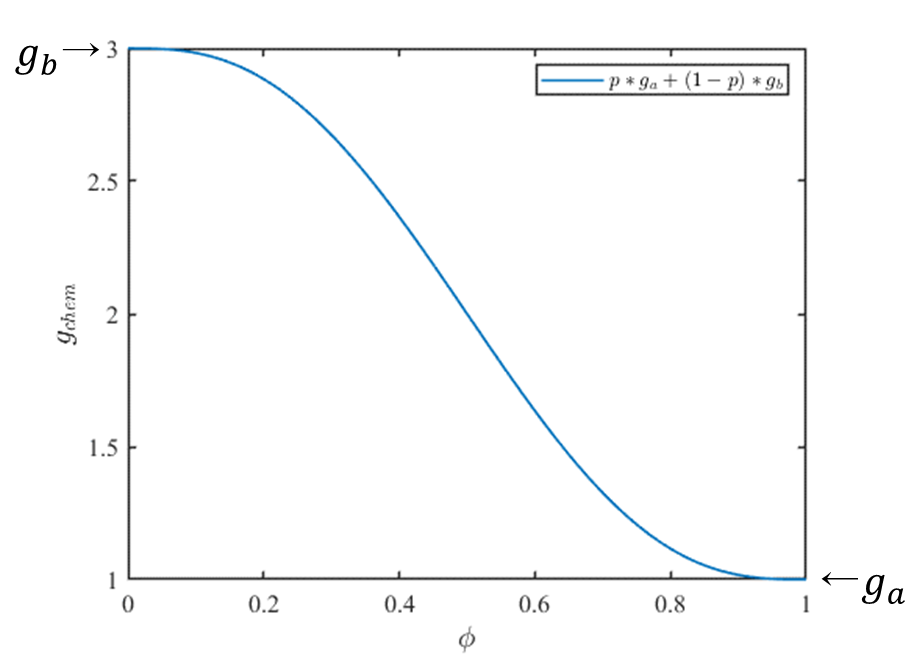
アレン-カーン方程式ではギブスの自由エネルギーを最小化するので、この場合、化学的自由エネルギー密度的にはよりエネルギーが低いa相(\(\phi=1)\)を実現しようとします。
\(g_{a},g_{b}\)は実際は組成や温度に依存し、正則溶体化近似により定式化されます。この辺りは以前まとめたCALPHAD法でも出てきた内容ですが、今の段階では簡単のため、定数として扱っておくことにしましょう。
ダブルウェルポテンシャル\(g_{doub}\)
化学的自由エネルギー密度のみ考えた場合、\(g_b>g_a\)が成り立つとき、エネルギー最小化の観点から、問答無用でa相が実現します。しかしながら、現実には過冷却現象に見られる準安定状態のように、ギブスのエネルギーが局所的に最小化されている状態が実現することがあります。このような状態を再現するために導入されるのが、ダブルウェルポテンシャル\(g_{doub}\)です。
\(g_{doub}\)は以下のような形で表されます。
g_{doub}&=Wq(\phi) \tag{11} \\
q(\phi)&=\phi ^2 (1-\phi)^2 \tag{12} \\
\end{align}
ここで\(W\)はダブルウェルポテンシャルの大きさを決める係数です。\(W=1\)として式\((11)\)をグラフ化すると次のようになります。
ダブルウェルポテンシャル\(g_{doub}\)は\(\phi=0.5\)でピークを持ち、\(\phi=0,1\)で０となる関数です。これは組織が相a(\(\phi=1\))から相b(\(\phi=0\))に変化する際に、相変化のエネルギーが必要であることを示しています。
化学的自由エネルギーとダブルウェルポテンシャルを足し合わせると式\((8),(11)\)より
g_{chem}+g_{doub}=p(\phi)g_{a}+(1-p(\phi))g_{b}+Wq(\phi) \tag{13} \\
\end{align}
ここで\(g_{a}=1,g_{b}=3,W=20\)として、上式をグラフ化してみます。
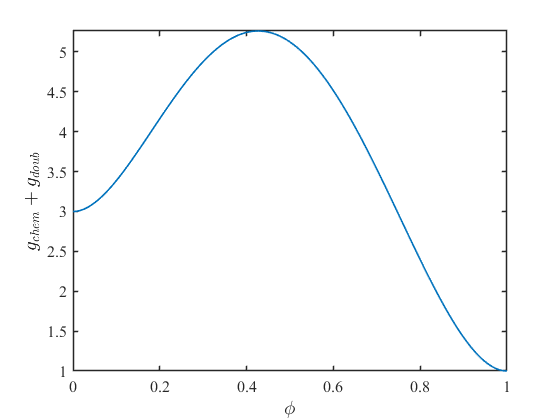
この場合、\(\phi=1\)で最小値（安定状態）、\(\phi=0\)で極小値（準安定状態）を取ります。このように、ダブルウェルポテンシャルを導入することで、エネルギー的な準安定状態を表現できるようになります。
勾配エネルギー密度\(g_{grad}\)
ここまではバルク状態（界面に触れていない部分）の組織のエネルギーについて議論してきました。しかし現実にはa相、b相の間に形成される界面のエネルギーも考える必要があります。フェーズフィールド法ではこれを勾配エネルギー密度\(g_{grad}\)として表現します。
界面のパラメーターとしてはその厚み（勾配\(\nabla \phi\)）と曲率（勾配の変化率\(\nabla ^2 \phi\)）が考えられます。したがって、界面の自由エネルギー\(g_{int}\)は次のように書いてよいでしょう。
g_{int}= K_{1}(\phi) \nabla^2\phi +K_{2}(\phi) (\nabla\phi )^2\tag{14}
\end{align}
ここで\(K_{1},K_{2}\)はそれぞれ界面の曲率、および勾配のエネルギーへの影響度合いを表す係数です。一般にこれらは\(\phi\)の関数となります。（ギブスの自由エネルギーは\(\phi\)の関数でもあるので、展開していない\(\phi\)の影響を\(K_{1},K_{2}\)に持たせています。）
また\(\nabla\phi\)はベクトルであり、\((\nabla\phi )^2=\nabla\phi \cdot \nabla\phi\)であることを注意します。
\(\nabla \phi\)が１乗ではなく２乗になっているのは、勾配の寄与は向きは問わず、大きさだけで決まるためです。例えば下図のように同等の勾配の大きさで相a（\(\phi = 1\)）から相b（\(\phi = 0\)）に変化する領域と、相b（\(\phi = 0\)）から相a（\(\phi = 1\)）に変化する領域が存在する時、それらはエネルギー的に等価というわけです。当たり前といえば当たり前ですね。
式\((13)\)はもう一段階スッキリさせることが出来ます。両辺を空間全体で積分し、全界面エネルギー\(G_{int}\)を考えます。
G_{int}= \int_{V}\left\{K_{1}(\phi) \nabla^2\phi +K_{2}(\phi) (\nabla\phi)^2\right\}dV\tag{15}
\end{align}
ここで第一項に部分積分（積の微分公式）を適用すると
\int_{V}K_{1}(\phi) \nabla^2\phi dV=\int_{V}\left\{\nabla \cdot \left(K_{1}(\phi) \nabla \phi \right)-\nabla K_{1}(\phi) \cdot\nabla\phi\right\} dV&
\tag{16}
\end{align}
さらにその第一項にガウスの発散定理を利用し
=\int_{S}K_{1}(\phi) \nabla \phi \cdot \boldsymbol{n} dS-\int_{V}\nabla K_{1}(\phi) \cdot\nabla\phi dV
\tag{17}
\end{align}
上記の\(\boldsymbol{n}\)は境界に垂直な方向（法線方向）の単位ベクトルです。
ここで計算領域が十分広く、領域境界周辺は常に平衡状態であると仮定し、境界において秩序変数の勾配は一定、すなわち\(\nabla \phi=0\)が成立するものとします。（これはノイマン条件に相当します。）
&=-\int_{V}\nabla K_{1}(\phi) \cdot\nabla\phi dV =-\int_{V} \frac{\partial K_{1}(\phi)}{\partial \phi}\nabla \phi \cdot\nabla\phi dV
=-\int_{V} \frac{\partial K_{1}(\phi)}{\partial \phi}(\nabla \phi)^2dV \\
\tag{18}
\end{align}
これを再び式\((15)\)に代入すると
G_{int}&= \int_{V}\left\{- \frac{\partial K_{1}(\phi)}{\partial \phi}(\nabla \phi)^2 +K_{2}(\phi) (\nabla\phi)^2\right\}dV\\
&= \int_{V}\left\{K_{2}(\phi) – \frac{\partial K_{1}(\phi)}{\partial \phi} \right\}(\nabla \phi)^2 dV\\
&= \int_{V}\frac{a^2}{2}(\nabla \phi)^2 dV\tag{19}
\end{align}
が得られます。ここで\(\frac{a^2}{2}= K_{2}(\phi) – \frac{\partial K_{1}(\phi)}{\partial \phi}
\)を表します。\(a\)は勾配係数と呼ばれる勾配エネルギーの大きさを決める係数で一般に正の値を取ります。係数の\(\frac{1}{2}\)は後で微分する際に２がかけられるので、それを打ち消すための係数です。
以上より勾配エネルギー密度\(g_{grad}\)は次式で与えられます。
g_{grad}= \frac{a^2}{2}(\nabla \phi)^2 \tag{20}
\end{align}
式\((14)\)の段階では、勾配の項\((\nabla \phi)^2\)と曲率の項\(\nabla^2 \phi\)が分離していましたが、最終的には曲率の項も\((\nabla \phi)^2\)にまとめられることが分かりました。\(a\)が正の定数だとすると、ギブスの自由エネルギー最小化の観点から、\((\nabla \phi)^2\)が小さくなる方向、つまり、界面の勾配が緩やかに、かつ曲率も小さくなる方向（凹凸があると円に近づく方向）に反応が進むことになります。
以上で冒頭で示した3種のギブズの自由エネルギー密度\(g_{chem},g_{doub},g_{grad}\)のすべてを導くことが出来ました。
おわりに
今回はアレンカーン方程式に現れるギブスの自由エネルギーのモデル化の主要部分について導出しました。物質の組織状態を再現するため、様々な形のエネルギーを導入していく点が興味深いです。次回は係数と物性値の関係づけについてまとめたいと思います。
参考文献
[1] 高木 知弘ら, “フェーズフィールド法”, 養賢堂, 2012/3/2
[2] 山中 晃徳ら, “Pythonによるフェーズフィールド法入門 基礎理論からデータ同化の実装まで”, 丸善出版, 2023/12/15
コメント