はじめに
前回記事ではアレン-カーン方程式\((1)\)で用いられるギブスの自由エネルギー\(G\)が化学的自由エネルギー密度\(g_{chem}\)、ダブルウェルポテンシャル\(g_{doub}\)、勾配エネルギー密度\(g_{grad}\)によってモデル化されることについてまとめました。
\frac{\partial \phi}{\partial t}&=-M_{\phi}\frac{\delta G}{\delta \phi} \tag{1}\\
G(\phi, \nabla\phi,\nabla ^2\phi)&=\int_V g(\phi, \nabla\phi,\nabla ^2\phi)dV\tag{2}\\
g&=g_{chem}+g_{doub}+g_{grad}\tag{3}\\
g_{chem}&=p(\phi)g_{a}+(1-p(\phi))g_{b}\tag{4}\\
g_{doub}&=Wq(\phi)\tag{5}\\
g_{grad}&=\frac{a^2}{2}(\nabla \phi)^2\tag{6}\\
p(\phi)&=\phi ^2(3-2\phi) \tag{7}\\
q(\phi)&=\phi ^2 (1-\phi)^2 \tag{8}
\end{align}
これらの定式化にはフェーズフィールドモビリティ\(M_{\phi}\)、エネルギー障壁\(W\)、勾配係数\(a\)といったパラメーターが用いられています。今回はこれらのパラメーターについて、より定量的な評価や具体的な意味付けを行うため、実際の物性値との関連付けを行います。
汎関数微分の計算
物性値との関係付けの前にアレン-カーン方程式\((1)\)をより分かりやすい形に変形しておきます。
アレン-カーン方程式\((1)\)を解くには、右辺の汎関数微分\(\frac{\delta G}{\delta \phi} \)を計算する必要があります。以前の記事にて触れた通り、ギブスの自由エネルギー\(G(\phi,\nabla \phi,\nabla^2 \phi)\)の汎関数微分はエネルギー密度\(g(\phi,\nabla \phi,\nabla^2 \phi)\)を用いて、次の通り書けました。
\frac{\delta G}{\delta \phi}=\frac{\partial g}{\partial \phi}
-\nabla \cdot
\left(\frac{\partial g}{\partial \left(\nabla \phi\right)}\right)
-\nabla ^2
\left(
\frac{\partial g}{\partial \left(\nabla ^2 \phi\right)}\right)
\tag{9}
\end{align}
\(\phi,\nabla \phi,\nabla^2 \phi\)が独立変数であることに注意し、各項を順に計算します。
\frac{\partial g}{\partial \phi}&=\frac{\partial }{\partial \phi}\left(p(\phi)g_{a}+(1-p(\phi))g_{b}+Wq(\phi)\right)\\
&=g_{a}\frac{\partial p(\phi)}{\partial \phi}-g_{b}\frac{\partial p(\phi)}{\partial \phi}+W\frac{\partial q(\phi)}{\partial \phi}\\
&=\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}+W\frac{\partial q(\phi)}{\partial \phi}\tag{10}
\end{align}
\nabla \cdot\left(\frac{\partial g}{\partial \left(\nabla \phi\right)}\right)&=\nabla \cdot\frac{\partial }{\partial \left(\nabla \phi\right)}\left(\frac{a^2}{2}(\nabla \phi)^2\right)\\
&=a^2\nabla \cdot\left(\nabla \phi\right)\\
&=a^2\nabla^2 \phi
\tag{11}
\end{align}
\nabla ^2
\left(
\frac{\partial g}{\partial \left(\nabla ^2 \phi\right)}\right)=0
\tag{12}
\end{align}
以上、式\((10)\sim(12)\)を式\((9)\)に代入すると汎関数微分は次の通り書けます。
\frac{\delta G}{\delta \phi}=\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}+W\frac{\partial q(\phi)}{\partial \phi}-a^2\nabla^2 \phi
\tag{13}
\end{align}
これを式\((1)\)に代入すると、アレン-カーン方程式は次のようになります。
\frac{\partial \phi}{\partial t}&=M_{\phi}\left[a^2\nabla^2 \phi-\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}-W\frac{\partial q(\phi)}{\partial \phi}\right] \tag{14}
\end{align}
上式よりアレン-カーン方程式は拡散方程式に何かしらの発生項（右辺第二、三項）を付加した方程式であるということが分かります。このタイプの方程式は「反応拡散方程式」として知られ、右辺第二、三項は「反応項」と呼ばれます。反応拡散方程式は反応項の特性によって解の挙動が変化します。
簡単のため、上記について１次元で考えると次式が得られます。
\frac{\partial \phi}{\partial t}&=M_{\phi}\left[a^2\frac{\partial^2 \phi}{\partial x^2} -\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}-W\frac{\partial q(\phi)}{\partial \phi}\right] \tag{15}\\
\end{align}
上式をベースに次節から物性値との関係付けを行います。
界面幅\(\delta\)との関連付け
異相間の界面は有限の幅\(\delta\)をもって存在しています。まずはこの\(\delta\)がアレン-カーン方程式\((15)\)上のどのパラメーターに支配されるのか１次元の平衡状態を例に考えてみましょう。
最もシンプルな界面の平衡状態として、下図のように原点を境にa相（\(\phi=1\)）とb相（\(\phi=0\)）が入れ替わる秩序変数の１次元プロファイル\(\phi(x)\)を想定します。
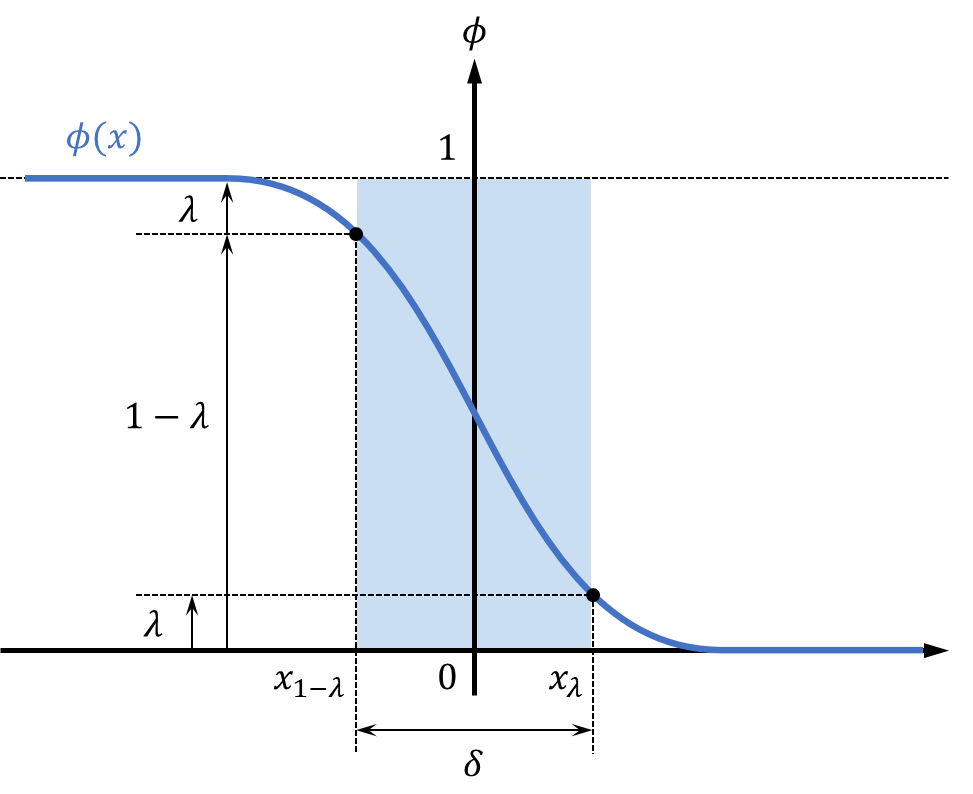
この時、\(\phi=\lambda \sim 1-\lambda\)の範囲を界面幅\(\delta= x_{\lambda}-x_{1-\lambda} \)と定義します。\(\lambda\)は一般的に\(0.1\)などの値を設定します。
定常的なアレン-カーン方程式からこのような解状態\(\phi(x)\)の具体的な形を定めることが出来ます。
まず、平衡状態なので\(\frac{\partial \phi}{\partial t}=0\)が成り立ちます。また、前回記事でも述べた通り、平衡状態では界面移動が停止するので、\(\Delta g =g_a-g_b=0 \)が成立します。したがって、アレン-カーン方程式\((15)\)は次のように簡略化されます。
\frac{\partial \phi}{\partial t}=M_{\phi}&\left[a^2\frac{\partial^2 \phi}{\partial x^2} -\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}-W\frac{\partial q(\phi)}{\partial \phi}\right]\\
&\rightarrow
a^2\frac{d^2 \phi}{d x^2}=W\frac{dq(\phi)}{d \phi}\tag{16}
\end{align}
上式両辺に\(\frac{d\phi}{dx}\)をかけて\(x\)で積分すると、
&a^2\int\frac{d^2 \phi}{d x^2}\frac{d\phi}{dx}dx=W\int\frac{dq(\phi)}{d \phi}\frac{d\phi}{dx}dx\tag{17}
\end{align}
この式の左辺と右辺はそれぞれ次のように計算できます。
（左辺）&＝a^2\int\frac{d^2 \phi}{d x^2}\frac{d\phi}{dx}dx=\frac{a^2}{2}\int\frac{d}{dx}\left(\frac{d \phi}{d x}\right)^2dx=\frac{a^2}{2}\left(\frac{d \phi}{d x}\right)^2+c_{1}\tag{18}\\
（右辺）&＝W\int\frac{dq(\phi)}{d \phi}\frac{d\phi}{dx}dx＝Wq(\phi)+c_{2}\tag{19}\\
\end{align}
ここで\(c_{i}(i=1,2\cdots)\)は積分定数です。したがって両辺を合わせると、
\frac{a^2}{2}\left(\frac{d \phi}{d x}\right)^2＝Wq(\phi)+c_{3}\tag{20}\\
\end{align}
が得られます。ここで\(x \rightarrow \pm \infty\)を考えると\(\frac{d \phi}{d x}=0\)なので\(c_{3}=0\)となります。また冒頭で想定した\(\phi (x)\)のプロファイルより、\(\frac{d\phi}{dx}\leq 0\)であることに注意すると次のようにまとめることが出来ます。
\frac{d \phi}{d x}&＝-\frac{\sqrt{2Wq(\phi)}}{a}\tag{21}
\end{align}
さらに式\((8)\)を代入すると、
&\frac{d \phi}{d x}＝-\frac{\sqrt{2W\phi ^2 (1-\phi)^2}}{a}\\
&\rightarrow
\frac{d \phi}{d x}＝-\frac{\sqrt{2W}}{a}\phi (1-\phi)\tag{22}
\end{align}
上式は変数分離法を使うことで\(\phi\)について解くことが出来ます。左辺に\(\phi\)、右辺に\(x\)を移動し、両辺を積分すると、
&\int \frac{1}{\phi (1-\phi)}d \phi＝-\frac{\sqrt{2W}}{a}\int dx\\
&\rightarrow
\int \frac{1}{\phi}+\frac{1}{(1-\phi)}d \phi＝-\frac{\sqrt{2W}}{a}\int dx\\
&\rightarrow
\log\left| \phi \right|-\log\left| 1-\phi \right|
＝-\frac{\sqrt{2W}}{a}x+c_{3}\\
&\rightarrow
\log\left| \frac{\phi}{ 1-\phi} \right|
＝-\frac{\sqrt{2W}}{a}x+c_{3}\\
&\rightarrow
\frac{\phi}{ 1-\phi}=\pm\exp\left(-\frac{\sqrt{2W}}{a}x+c_{3}\right)
\\
&\rightarrow
\frac{\phi}{ 1-\phi}=c_{4}\exp\left(-\frac{\sqrt{2W}}{a}x\right)
\tag{23}
\end{align}
ここでいったん任意定数\(c_{4}\)を消しておきます。上式に\(\phi(0)=\frac{1}{2}\)の条件を用いると\(c_{4}=1\)になるので、
&\frac{\phi}{ 1-\phi}=\exp\left(-\frac{\sqrt{2W}}{a}x\right) \\
&\rightarrow
\phi=(1-\phi)\exp\left(-\frac{\sqrt{2W}}{a}x\right) \\
&\rightarrow
\phi=\exp\left(-\frac{\sqrt{2W}}{a}x\right)-\phi \exp\left(-\frac{\sqrt{2W}}{a}x\right) \\
&\rightarrow
\phi\left\{1+ \exp\left(-\frac{\sqrt{2W}}{a}x\right) \right\}=\exp\left(-\frac{\sqrt{2W}}{a}x\right)\\
&\rightarrow
\phi=\frac{\exp\left(-\frac{\sqrt{2W}}{a}x\right)}{1+\exp\left(-\frac{\sqrt{2W}}{a}x\right) }\\
&\qquad=\frac{1}{\exp\left(\frac{\sqrt{2W}}{a}x\right)+1 }\\
&\qquad=\frac{1}{2}\left\{1-\frac{\exp\left(\frac{\sqrt{2W}}{2a}x\right)-\exp\left(-\frac{\sqrt{2W}}{2a}x\right)}{\exp\left(\frac{\sqrt{2W}}{2a}x\right)+\exp\left(-\frac{\sqrt{2W}}{2a}x\right) }\right\}\\
&\qquad=\frac{1}{2}\left\{1-\tanh\left(\frac{\sqrt{2W}}{2a}x\right)\right\}\tag{24}
\end{align}
少々長くなりましたが以上で\(\phi\)の具体的な形を定めることが出来ました。もうひと踏ん張りです。
ここからは\(\phi(x_{\lambda})=\lambda,\phi(x_{1-\lambda})=1-\lambda\)の関係を用いて、係数と\(\lambda\)の対応付けを行います。
\(\phi(x_{\lambda})=\lambda\)を式\((24)\)に代入すると
&\lambda=\frac{1}{2}\left\{1-\tanh\left(\frac{\sqrt{2W}}{2a}x_{\lambda}\right)\right\}\\
&\rightarrow
1-2\lambda=\tanh\left(\frac{\sqrt{2W}}{2a}x_{\lambda}\right)\\
&\rightarrow
\frac{\sqrt{2W}}{2a}x_{\lambda}=\tanh^{-1}\left(1-2\lambda\right)\\
&\rightarrow
x_{\lambda}=\frac{\sqrt{2}a}{\sqrt{W}}\tanh^{-1}\left(1-2\lambda\right)
\tag{25}
\end{align}
同様に\(\phi(x_{1-\lambda})=1-\lambda\)を式\((24)\)に代入すると
&1-\lambda=\frac{1}{2}\left\{1-\tanh\left(\frac{\sqrt{2W}}{2a}x_{1-\lambda}\right)\right\}\\
&\rightarrow
1-2\lambda=-\tanh\left(\frac{\sqrt{2W}}{2a}x_{1-\lambda}\right)\\
&\rightarrow
1-2\lambda=\tanh\left(-\frac{\sqrt{2W}}{2a}x_{1-\lambda}\right)\\
&\rightarrow
-\frac{\sqrt{2W}}{2a}x_{1-\lambda}=\tanh^{-1}\left(1-2\lambda\right)\\
&\rightarrow
x_{1-\lambda}=-\frac{\sqrt{2}a}{\sqrt{W}}\tanh^{-1}\left(1-2\lambda\right)
\tag{26}
\end{align}
上式\((25),(26)\)より界面幅\(\delta = x_{\lambda}-x_{1-\lambda}\)が次の通り計算できます。
\delta &= x_{\lambda}-x_{1-\lambda}\\
&= \frac{\sqrt{2}a}{\sqrt{W}}\tanh^{-1}\left(1-2\lambda\right)+\frac{\sqrt{2}a}{\sqrt{W}}\tanh^{-1}\left(1-2\lambda\right)\\
&= \frac{\sqrt{2}a}{\sqrt{W}}b
\tag{27}
\end{align}
ここで\(b=2\tanh^{-1}\left(1-2\lambda\right)\)です。例えば\(\lambda=0.1\)とすると\(b \sim 2.2\)になります。
以上で界面幅\(\delta\)とエネルギー障壁\(W\)、勾配係数\(a\)の関連付けが出来ました。
\(\delta\)は\(W\)が大きくなるほど小さくなります。これはエネルギー障壁\(W\)が大きいほど、相が混ざり合いづらくなり、界面幅\(\delta\)が小さくなるためと考えられます。また、\(\delta\)は\(a\)が大きくなるほど大きくなります。式\((15)\)から見ても\(a\)はいわゆる「拡散係数」に対応するため、これが大きいと全体的に解が鈍る（\(\delta\)が大きくなる）方向に行くのは理解しやすい関係です。
界面エネルギー\(\gamma\)との関連付け
次は界面エネルギー\(\gamma\)と各係数の関連付けについて考えます。3種のギブスの自由エネルギー密度\(g_{chem},g_{doub},g_{grad}\)のうち、化学的自由エネルギーは\(g_{chem}\)はバルク状態（界面に触れていない部分）のエネルギーであり、各元素の配置エントロピーや結合力から計算されます。
したがって界面に関連する部分のエネルギーの総和\(\gamma\)は、式\((2),(3),(5),(6)\)から\(g_{chem}\)を除き、次のように書けます。
\gamma&=\int_{-\infty}^{\infty} \left(g_{doub}+g_{grad}\right)dx\\
&=\int_{-\infty}^{\infty}\left[Wq(\phi)+\frac{a^2}{2}\left(\frac{d\phi}{dx}\right)^2 \right]dx\tag{28}\\
\end{align}
上式は簡単のため、1次元の式として考えています。さらに平衡状態を仮定すると、式\((21)\)より次の関係式が成り立ちます。
&\frac{d \phi}{d x}＝-\frac{\sqrt{2Wq(\phi)}}{a}\\
&\rightarrow
\left(\frac{d\phi}{dx}\right)^2 ＝\frac{2Wq(\phi)}{a^2}\\
&\rightarrow
\frac{a^2}{2}\left(\frac{d\phi}{dx}\right)^2 ＝Wq(\phi)
\tag{29}
\end{align}
これを式\((28)\)に代入すると、
\gamma&=\int_{-\infty}^{\infty}\left[Wq(\phi)+Wq(\phi)\right]dx\\
&=2W\int_{-\infty}^{\infty}q(\phi)dx\\
&=2W\int_{1}^{0}q(\phi)\frac{dx}{d\phi}d\phi
\tag{30}
\end{align}
上式に式\((8),(22)\)を代入すると、
\gamma&=2W\int_{1}^{0}\phi ^2 (1-\phi)^2 \left(-\frac{\sqrt{2W}}{a}\phi (1-\phi)\right)^{-1}d\phi\\
&=-\frac{2Wa}{\sqrt{2W}}\int_{1}^{0}\phi (1-\phi)d\phi\\
&=-\frac{2a\sqrt{W}}{\sqrt{2}}\int_{1}^{0}\phi (1-\phi)d\phi\\
&=-\frac{2a\sqrt{W}}{\sqrt{2}}\left[\frac{1}{2}\phi ^2-\frac{1}{3}\phi ^3\right]_{1}^{0} \\
&=-\frac{2a\sqrt{W}}{\sqrt{2}}\left(-\frac{1}{2}+\frac{1}{3}\right)\\
&=\frac{a\sqrt{W}}{3\sqrt{2}}
\tag{31}
\end{align}
以上で界面エネルギー\(\gamma\)とエネルギー障壁\(W\)、勾配係数\(a\)の関連付けが出来ました。
\(\gamma\)は\(W\)が大きいほど大きくなります。これはエネルギー障壁\(W\)が大きいほど、相状態の変化にエネルギーを要するため、その界面を形成するのに必要なエネルギー（界面エネルギー）も大きくなることを示しています。また、\(\gamma\)は\(a\)が大きいほど大きくなります。これは勾配係数\(a\)が大きいほど、界面がより広範囲にわたって平滑化され、表面積が増加するため、界面エネルギーも大きくなることを示しています。
界面モビリティ\(M\)との関連付け
前回記事でも述べた通り、二つの相a,bの化学的自由エネルギー\(g_{a},g_{b}\)に差があるとき、界面はエネルギーの低い相から高い相に向かって移動することが知られています。この時、界面の移動速度\(V\)は、界面モビリティ\(M\)によって次のように特徴づけられました。
V=M\Delta g\\
\tag{32}
\end{align}
ここで\(\Delta g =g_{a}-g_{b}\)は化学的駆動力（2つの化学的自由エネルギー密度の差）を表します。
最後にこの界面モビリティ\(M\)と各係数の対応付けを考えます。
式\((24)\)のような平衡プロファイルを有する界面が、一定速度\(V\)で\(+x\)方向に移動する定常成長問題を考えます。このときプロファイルは\(\phi(x-Vt)\)と書けるので、次式が成り立ちます。
\frac{d\phi}{dt}=\frac{d\phi}{dx}\frac{dx}{dt}=-V\frac{d\phi}{dx}\\
\tag{33}
\end{align}
上式を式\((15)\)に代入すると、
&\frac{d \phi}{\partial t}=M_{\phi}\left[a^2\frac{d^2 \phi}{dx^2} -\left(g_{a}-g_{b}\right)\frac{dp(\phi)}{d \phi}-W\frac{d q(\phi)}{d \phi}\right]\\
&\rightarrow
-V\frac{d\phi}{dx}=M_{\phi}\left[a^2\frac{d^2 \phi}{dx^2} -\left(g_{a}-g_{b}\right)\frac{d p(\phi)}{d\phi}-W\frac{d q(\phi)}{d \phi}\right]\tag{34}
\end{align}
を得る。\(\phi\)は平衡状態のプロファイル（式\((24)\)）を仮定しており、式\((16)\)も成り立つので、上式にこれを代入すると、
&-V\frac{d\phi}{dx}=M_{\phi}\left[W\frac{dq(\phi)}{d \phi} -\left(g_{a}-g_{b}\right)\frac{d p(\phi)}{d \phi}-W\frac{d q(\phi)}{d \phi}\right]\\
&\rightarrow
-V\frac{d\phi}{dx}=M_{\phi}\left[ -\left(g_{a}-g_{b}\right)\frac{d p(\phi)}{d \phi}\right]
\tag{35}
\end{align}
さらに両辺に\(\frac{d\phi}{dx}\)を掛けて\(x\)で積分すると、
&V\int_{-\infty}^{\infty}\left(\frac{d\phi}{dx}\right)^2dx=M_{\phi}\left(g_{a}-g_{b}\right)\int_{-\infty}^{\infty}\frac{d p(\phi)}{d \phi}\frac{d\phi}{dx}dx\\
\rightarrow
&V\int_{1}^{0}\left(\frac{d\phi}{dx}\right)d\phi=M_{\phi}\left(g_{a}-g_{b}\right)\int_{0}^{1}d p
\tag{36}
\end{align}
左辺に式\((22)\)を代入し、
&V\int_{1}^{0}\left[-\frac{\sqrt{2W}}{a}\phi (1-\phi)\right]d\phi=M_{\phi}\left(g_{a}-g_{b}\right)\int_{0}^{1}d p\\
&\rightarrow
-\frac{\sqrt{2W}}{a}V\int_{1}^{0}\phi (1-\phi)d\phi=M_{\phi}\left(g_{a}-g_{b}\right)\int_{0}^{1}d p\\
&\rightarrow
-\frac{\sqrt{2W}}{a}V\left[\frac{1}{2}\phi^2 -\frac{1}{3}\phi ^3\right]_{1}^{0}=M_{\phi}\left(g_{a}-g_{b}\right)\\
&\rightarrow
\frac{\sqrt{2W}}{6a}V=M_{\phi}\left(g_{a}-g_{b}\right)\\
&\rightarrow
V=\frac{6a}{\sqrt{2W}}M_{\phi}\Delta g
\tag{37}
\end{align}
上式と式\((32)\)を比較すると、界面モビリティ\(M\)は次のように書けます。
M=\frac{6a}{\sqrt{2W}}M_{\phi}
\tag{38}
\end{align}
以上で界面モビリティ\(M\)とエネルギー障壁\(W\)、勾配係数\(a\)、フェーズフィールドモビリティ\(M_{\phi}\)の関連付けが出来ました。
\(M\)は\(W\)が大きいほど小さくなります。これはエネルギー障壁\(W\)が大きいほど、異なる相への移行が妨げられ、界面が動きづらくなることを示しています。また、\(M\)は\(a\)が大きいほど大きくなります。これは勾配係数\(a\)が大きいほど、界面が広くなり、物質の拡散や運動が活発になることを示しています。
まとめ
ここまでに求めた関係式をまとめると次の通りです。
\delta &= \frac{\sqrt{2}a}{\sqrt{W}}b
\tag{39}\\
\gamma&=\frac{a\sqrt{W}}{3\sqrt{2}}
\tag{40}\\
M&=\frac{6a}{\sqrt{2W}}M_{\phi}
\tag{41}\\
\end{align}
これらをさらに\(a,W,M_{\phi}\)についてまとめなおすと次のように書けます。
a &= \sqrt{\frac{3\delta \gamma}{b}}
\tag{42}\\
W&=\frac{6\gamma b}{\delta}
\tag{43}\\
M_{\phi}&=\frac{b}{3\delta}M
\tag{44}\\
\end{align}
以上のようにフェーズフィールド法では支配方程式中に現れる係数を物性値と関連付けることが出来るため、定量的な評価が可能となります。ただし、これらは化学的駆動力\(\Delta g\)が界面領域内で一定の時だけ成り立つ関係式であり、界面領域内で温度や濃度が変化するような条件では別の議論が必要となります。
おわりに
今回はフェーズフィールド法では支配方程式中に現れる係数と物性値の関連付けについてまとめました。アレン-カーン方程式は拡散方程式と比較して複雑な形をしているため、各項の影響が理解しづらい面があります。そのような時に今回のように物理量と紐づけることで、より直感的な理解を得ることが可能です。次回はアレン-カーン方程式を実際に解いてみたいと思います。
参考文献
[1] 高木 知弘ら, “フェーズフィールド法”, 養賢堂, 2012/3/2
[2] 山中 晃徳ら, “Pythonによるフェーズフィールド法入門 基礎理論からデータ同化の実装まで”, 丸善出版, 2023/12/15
コメント