はじめに
前回記事では、2元合金の凝固の導入として正則溶体近似とWBMモデルの概要ついてまとめました。中でも正則溶体近似は合金のギブスの自由エネルギーを与える最も基本的なモデルです。本記事では、正則溶体近似を用いて2元合金のアレン-カーン方程式を導出します。
2元合金の化学的駆動力
前回記事で述べた通り、2元合金の凝固を解くには、その化学的駆動力を求める必要がありました。
\frac{\partial \phi}{\partial t}&=-M_{\phi}\left[30\underbrace{\left(g_{S}-g_{L}\right)}_{chemical \ driving \ force}\phi^2\left(1-\phi\right)^2+2W\phi (1-\phi)(1-2\phi)
\right.\\
&\left. \quad\quad\quad\quad\quad-2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
\right.\\
&\left.\quad\quad\quad\quad\quad\quad
-\frac{\partial }{\partial x}\left( a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial x}
\right)
\right]
\tag{1}
\end{align}
これを求めるため、今一度ギブスの自由エネルギーの定義に立ち返ります。一般にギブスの自由エネルギー\(G\)\(\rm{[J/mol]}\)はエンタルピー\(H\)\(\rm{[J/mol]}\)、エントロピー\(S\)\(\rm{[J/mol\cdot K]}\)、温度\(T\)\(\rm{[K]}\)を用いて、以下のように与えられました。
G=H-TS\tag{2}
\end{align}
上式が2元合金の場合にどうなるか、改めて考える必要があるわけです。
ここで天下りではありますが、以下に最終的に求まる2元合金におけるギブスの自由エネルギ―の形を示します。
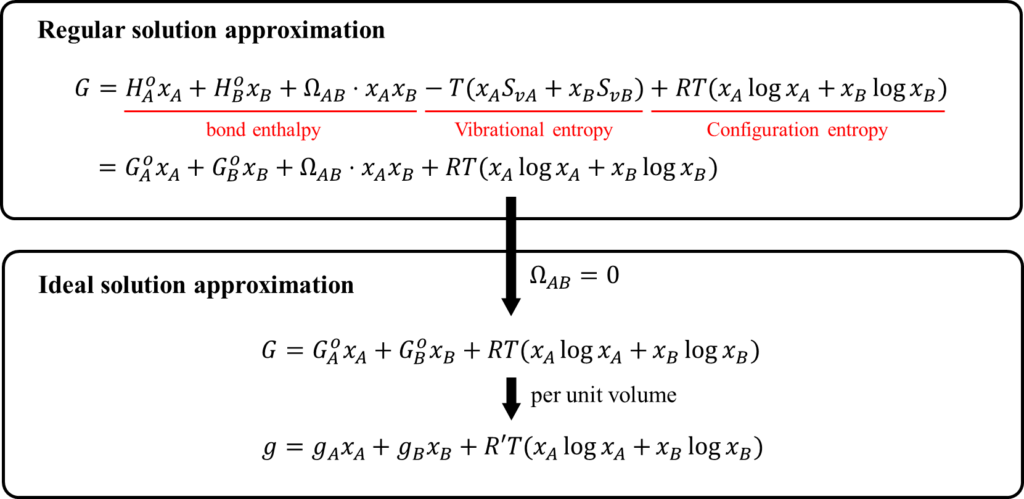
2元合金の自由エネルギーは正則溶体近似(Regular solution approximation)により計算できます。正則溶体近似は合金におけるギブスの自由エネルギーを与える最も基本的なモデルの一つで、結合エンタルピー(Bond enthalpy)、振動エントロピー(Vibrational entropy)、配置エントロピー(Configuration entropy)からなります。
また、フェーズフィールド法では、正則溶体近似をさらに簡略化した理想溶体近似(Ideal solution approximation)を用いる場合があります。
次節以降、これらの導出を行っていきましょう。
結合エンタルピー
まず、式\((2)\)中のエンタルピー\(H\)について考えましょう。合金では異なる金属間での結合が生じるため、純物質とは異なる内部エネルギーを有します。
今、無作為に混合された原子A,Bが最近接原子間で相互作用する場合について考えましょう。この時、系の内部エネルギー\(E\)は次式で与えられます。
E=N_{AA}e_{AA}+N_{BB}e_{BB}+N_{AB}e_{AB}\tag{3}
\end{align}
ここで、A-A、B-B、A-Bの原子対の数を\(N_{AA},N_{BB},N_{AB}\)、結合によるエネルギーを\(e_{AA},e_{BB},e_{AB}\)としています。
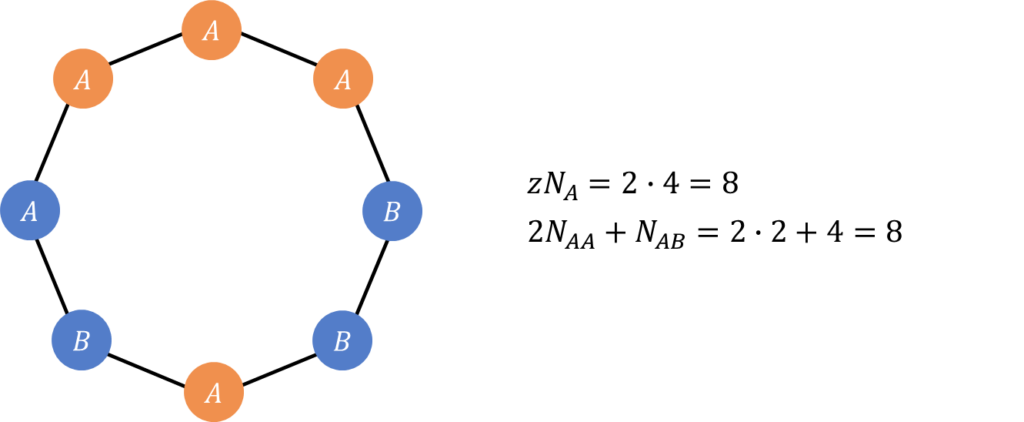
次に、各金属原子から出ている結合手の数\(z\)について考えます。金属A,Bの原子数を\(N_{A},N_{B}\)とおくと、各元素の結合手の総数は\(zN_{A},zN_{B}\)と書いてよいでしょう。したがって、各原子対の数\(N_{AA},N_{BB},N_{AB}\)との間には次式が成り立ちます。
zN_{A}=2N_{AA}+N_{AB}\rightarrow N_{AA}=\frac{1}{2}zN_{A}-\frac{1}{2}N_{AB}\tag{4}\\
zN_{B}=2N_{BB}+N_{AB}\rightarrow N_{BB}=\frac{1}{2}zN_{B}-\frac{1}{2}N_{AB}\tag{5}\\
\end{align}
例えば下図のような\(z=2\)の1次元結合で考えると上式が成り立つことが分かりやすいです。
式\((4),(5)\)を式\((3)\)に代入すると、
E&=\left(\frac{1}{2}zN_{A}-\frac{1}{2}N_{AB}\right)e_{AA}+\left(\frac{1}{2}zN_{B}-\frac{1}{2}N_{AB}\right)e_{BB}+N_{AB}e_{AB}\\
&=\frac{1}{2}zN_{A}e_{AA}+\frac{1}{2}zN_{B}e_{BB}-\frac{1}{2}e_{AA}N_{AB}-\frac{1}{2}N_{AB}e_{BB}+N_{AB}e_{AB}\\
&=\frac{1}{2}zN_{A}e_{AA}+\frac{1}{2}zN_{B}e_{BB}+N_{AB}\left(e_{AB}-\frac{e_{AA}+e_{BB}}{2}\right)
\tag{6}
\end{align}
さらに、濃度(モル分率)\(x_{A},x_{B}\)、全原子数\(N(=N_{A}+N_{B})\)を用いると、各原子数\(N_{A},N_{B}\)は次のように書けます。
N_{A}&=Nx_{A} \tag{7}\\
N_{B}&=Nx_{B} \tag{8}\\
\end{align}
また、原子A、Bは無作為に混合されている(特定の原子が局所的な分布をしたりしない)ため、原子Aの\(z\)本の結合手の中で、A-B原子対となる数は原子Bの濃度(モル分率)の比率だけがあるはずです。したがって、A-B原子対の数\(N_{AB}\)は次式で計算できます。
N_{AB}&=N_{A}\cdot zx_{B}=Nx_{A}\cdot zx_{B} =zNx_{A}x_{B} \tag{9}\\
\end{align}
上式\((7)\sim(9)\)を式\((6)\)に代入すると
E&=\frac{1}{2}zNe_{AA}x_{A}+\frac{1}{2}zNe_{BB}x_{B}+zN\left(e_{AB}-\frac{e_{AA}+e_{BB}}{2}\right)x_{A}x_{B}\\
&=E_{A}^{o}x_{A}+E_{B}^{o}x_{B}+\Omega_{AB}x_{A}x_{B}\tag{10}
\end{align}
ここで、\(E_{A}^{o}x_{A}=\frac{1}{2}zNe_{AA},E_{B}^{o}x_{B}=\frac{1}{2}zNe_{BB}\)は\(N\)個の全原子が原子Aのみ、もしくは原子Bのみの系の内部エネルギーを表します。
また、\(\Omega_{AB}=zN\left(e_{AB}-\frac{e_{AA}+e_{BB}}{2}\right)\)は相互作用パラメーターと呼ばれ、式\((10)\)の右辺第三項はA、B原子が混合したことにより生じるエネルギーを表します。
最後に、式\((10)\)を式\((2)\)に代入するためにエンタルピー\(H\)へと書き換えます。エンタルピー\(H\)は一般に次式で与えられました。
H=E+PV\tag{11}
\end{align}
ただし、固体や液体においては、\(PV\)項は通常\(E\)に比べて、十分小さいため、\(H\sim E\)と考えることが出来ます。したがって、単純に式\((10)\)中の\(E\)を\(H\)に置き換えることが出来ます。
H&=H_{A}^{o}x_{A}+H_{B}^{o}x_{B}+\Omega_{AB}x_{A}x_{B}\tag{12}
\end{align}
以上で2元合金のエンタルピーを求めることが出来ました。
振動エントロピー
次に、式\((2)\)中のエントロピー\(S\)について考えましょう。任意の温度において、原子Aと原子Bはそれぞれ熱振動しています。量子力学で記述されるように原子の振動エネルギーは離散的な値を取ります。この離散化された振動エネルギーは、エネルギー準位として記述され、各準位に固有の状態数があります。
原子A、Bの振動の状態数を\(W_{A},W_{B}\)、個数を\(N_{A},N_{B}\)とすると、系の熱振動の状態数の総数\(W_{v}\)は
W_{v}&=W_{A}^{N_{A}}W_{B}^{N_{B}}\tag{13}
\end{align}
と表されます。上式をエントロピーの定義
S&=k\log W\tag{14}
\end{align}
に代入すると振動エントロピー\(S_{v}\)は次式で計算できます。
S_{v}&=k\log \left(W_{A}^{N_{A}}W_{B}^{N_{B}}\right)\\
&=k\left(N_{A}\log W_{A}+N_{B}\log W_{B}\right)\\
&=k\left(x_{A}N\log W_{A}+x_{B}N\log W_{B}\right)
\tag{15}
\end{align}
ここで1モルの原子Aと1モルの原子Bの振動エントロピーをそれぞれ、\(S_{vA}=kN\log W_{A},S_{vB}=kN\log W_{B}\)とおくと、
S_{v}&=x_{A}S_{vA}+x_{B}S_{vB}
\tag{16}\\
\end{align}
と表すことが出来ます。
配置エントロピー
2元合金におけるエントロピーの増加は、振動エントロピーだけではありません。原子の配置状態によっても取り得る状態数は増加します。
\(N_{A}\)個の原子Aと\(N_{B}\)個の原子Bを格子状にランダムに配置する場合、その組み合わせ数\(W_{AB}\)は、
W_{AB}=_{N}C_{N_{A}}&=\frac{N!}{N_{A}!(N-N_{A})!}=\frac{N!}{N_{A}!N_{B}!}\tag{17}
\end{align}
となります。したがって、式\((14)\)より配置によるエントロピー\(S_{c}\)を計算すると
S_{c}&=k\log \left(\frac{N!}{N_{A}!N_{B}!}\right)\\
&=k\left(\log N! – \log N_{A}! -\log N_{B}!\right) \tag{18}
\end{align}
ここで\(N\)が十分大きい場合、以下のスターリングの公式が成り立ちます。
\log N!&\sim N \log N – N\tag{19}
\end{align}
これを式\((18)\)に代入すると、
S_{c}&\sim k\left( N \log N – N – N_{A} \log N_{A} + N_{A} -N_{B} \log N_{B} + N_{B}\right)\\
&=k\left( N \log N – N_{A} \log N_{A} -N_{B} \log N_{B} \right)
\tag{20}
\end{align}
さらに式\((7),(8)\)を代入し、
S_{c}&=k\left( N \log N – Nx_{A} \log Nx_{A} -Nx_{B} \log Nx_{B} \right)\\
&=kN\left( \log N – x_{A} \log Nx_{A} -x_{B} \log Nx_{B} \right)\\
&=kN\left( \log N – x_{A} \log N- x_{A} \log x_{A} -x_{B} \log N-x_{B} \log x_{B} \right)\\
&=kN\left \{ (1- x_{A}- x_{B})\log N – x_{A} \log x_{A} -x_{B} \log x_{B} \right \} \\
&= -kN\left ( x_{A} \log x_{A} +x_{B} \log x_{B} \right )
\tag{21}
\end{align}
ここまでの変形で大分シンプルな形になりました。最後に、1モル当たりの配置エントロピーを考えると、\(N\)はアボガドロ数となるので、ガス定数の定義\(R=kN\)より、
S_{c}&=-R\left ( x_{A} \log x_{A} +x_{B} \log x_{B} \right )
\tag{22}
\end{align}
となります。以上で配置によるエントロピーを計算することが出来ました。
正則溶体近似
以上で2元合金のエンタルピーとエントロピーを求めることが出来ました。式\((2)\)に式\((12),(16),(22)\)代入すると、ギブスの自由エネルギーが計算できます。
G&=H-TS\\
&=H-T\left(S_{v}+S_{c}\right)\\
&=H_{A}^{o}x_{A}+H_{B}^{o}x_{B}+\Omega_{AB}x_{A}x_{B}-T\left(x_{A}S_{vA}+x_{B}S_{vB}\right)+RT\left ( x_{A} \log x_{A} +x_{B} \log x_{B} \right ) \\
&=\left(H_{A}^{o}-TS_{vA}\right)x_{A}+\left(H_{B}^{o}-TS_{vB}\right)x_{B}+\Omega_{AB}x_{A}x_{B}+RT\left ( x_{A} \log x_{A} +x_{B} \log x_{B} \right ) \tag{23}
\end{align}
この中で、原子A,Bが混合したことによって生じた項は右辺第三、四項です。逆に第一、二項は単体の原子A、Bがもつ1モル当たりギブスの自由エネルギーとみなすことが出来ます。
したがって、第一、二項の係数は\(G_{A}^{o}=H_{A}^{o}-TS_{vA},G_{B}^{o}=H_{B}^{o}-TS_{vB}\)とまとめておくこととしましょう。
G&=G_{A}^{o}x_{A}+G_{B}^{o}x_{B}+\Omega_{AB}x_{A}x_{B}+RT\left ( x_{A} \log x_{A} +x_{B} \log x_{B} \right ) \tag{24}
\end{align}
以上のように、
・相互作用は最近接原子間のみで生じる(最近接仮定)
・原子A、Bの存在確率は濃度\(x_{A},x_{B}\)に等しい(ランダム分布仮定)
を考慮して導かれる自由エネルギーの近似方法を正則溶体近似と呼びます。
理想溶体近似
さらに簡略化するため、A-A、B-B、A-B原子対の結合エネルギーがすべて等しく、\(e_{AA}=e_{BB}=e_{AB}\)が成り立つとしましょう。このとき、式\((10)\)より\(\Omega _{AB}=0\)となり、自由エネルギーは次式のように書けます。
G&=G_{A}^{o}x_{A}+G_{B}^{o}x_{B}+RT\left ( x_{A} \log x_{A} +x_{B} \log x_{B} \right ) \tag{25}
\end{align}
上記のように、正則溶体近似に加え、原子間相互作用を0とする近似を理想溶体近似と呼びます。
最後に単位系をそろえましょう。アレン-カーン方程式\((1)\)で用いられる自由エネルギーは自由エネルギー密度\(g_{S},g_{L}\rm{[J/m^3]}\)の次元です。
対して、式\((25)\)の自由エネルギーの次元は\(\rm{[J/mol]}\)でした。そこで、式\((24)\)の両辺を1モルあたりの体積\(v_{m}\rm{[m^3/mol]}\)で除します。
g&=g_{A}x_{A}+g_{B}x_{B}+R^{\prime}T\left ( x_{A} \log x_{A} +x_{B} \log x_{B} \right ) \tag{26}
\end{align}
ここで、\(g=\frac{G}{v_{m}},g_{A}=\frac{G_{A}^{o}}{v_{m}},g_{B}=\frac{G_{B}^{o}}{v_{m}},R^{\prime}=\frac{R}{v_{m}}\)を表します。
以上で2元合金のフェーズフィールド法で用いられる、化学的自由エネルギー密度の定式化が得られました。
上式を用いると、固相・液相の化学的自由エネルギー密度は次式のように与えられます。
g_{S}&=g_{S}^{A}x_{A}+g_{S}^{B}x_{B}+R^{\prime}T\left ( x_{A} \log x_{A} +x_{B} \log x_{B} \right ) \\
g_{L}&=g_{L}^{A}x_{A}+g_{L}^{B}x_{B}+R^{\prime}T\left ( x_{A} \log x_{A} +x_{B} \log x_{B} \right ) \\
\tag{27}
\end{align}
今回は1モデルあたりのエネルギーを考えているので、モル分率\(x_{A},x_{B}\)の間には\(x_{A}+x_{B}=1\)の関係が成り立ちます。したがって、\(x_{A}\)を消去して次式のように書いてもよいでしょう。
g_{S}&=g_{S}^{A}\left(1-x_{B}\right)+g_{S}^{B}x_{B}+R^{\prime}T\left [ \left(1-x_{B}\right) \log x_{A} +x_{B} \log x_{B} \right ] \\
g_{L}&=g_{L}^{A}\left(1-x_{B}\right)+g_{L}^{B}x_{B}+R^{\prime}T\left [ \left(1-x_{B}\right) \log x_{A} +x_{B} \log x_{B} \right ] \\
\tag{28}
\end{align}
アレン-カーン方程式の修正
ギブスの自由エネルギーの理想溶体近似が求まったので、これをアレン-カーン方程式\((1)\)に組み込みます。
式\((28)\)よりアレン-カーン方程式\((1)\)右辺第一項の化学的駆動力\(\Delta g = g_{S}-g_{L}\)は、
\Delta g &= g_{S}-g_{L}\\
&= g_{S}^{A}\left(1-x_{B}\right)+g_{S}^{B}x_{B}-g_{A}^{L}\left(1-x_{B}\right)-g_{B}^{L}x_{B}\\
&= \left(g_{S}^{A}-g_{L}^{A}\right)\left(1-x_{B}\right)+\left(g_{S}^{B}-g_{L}^{B}\right)x_{B}
\tag{29}
\end{align}
と書くことが出来ます。
また、\(g_{S}^{A}-g_{L}^{A},g_{S}^{B}-g_{L}^{B}\)は、それぞれ純粋な原子Aと原子Bの凝固の駆動力であり、潜熱分だけ異なるとし、次のように与えられます。
g_{S}^{A}-g_{L}^{A}=\frac{L_{A}\left(T-T_{m,A}\right)}{T_{m,A}}\\
g_{S}^{B}-g_{L}^{B}=\frac{L_{B}\left(T-T_{m,B}\right)}{T_{m,B}}\\
\tag{30}
\end{align}
ここで、\(L_{A},L_{B}\)は純粋な原子A、Bの潜熱、\(T_{m,A},T_{m,B}\)は純粋な原子A、原子Bの融点を表します。
したがって、式\((29)\)より化学的駆動力\(\Delta g\)は以下のように計算できます。
\Delta g &= g_{S}-g_{L}\\
&= \frac{L_{A}\left(T-T_{m,A}\right)}{T_{m,A}}\left(1-x_{B}\right)+\frac{L_{B}\left(T-T_{m,B}\right)}{T_{m,B}}x_{B}
\tag{31}
\end{align}
上式をアレン-カーン方程式\((1)\)に代入すると、
\frac{\partial \phi}{\partial t}&=-M_{\phi}\left[30\left\{ \frac{L_{A}\left(T-T_{m,A}\right)}{T_{m,A}}\left(1-x_{B}\right)+\frac{L_{B}\left(T-T_{m,B}\right)}{T_{m,B}}x_{B}\right\}\phi^2\left(1-\phi\right)^2\right.\\
&\left. \quad\quad\quad\quad\quad+2W\phi (1-\phi)(1-2\phi)-2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
\right.\\
&\left.\quad\quad\quad\quad\quad\quad
-\frac{\partial }{\partial x}\left( a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial x}
\right)
\right]
\tag{32}
\end{align}
以上で、アレン-カーン方程式に2元合金の化学的駆動力を組み込むことが出来ました。
まだ終わりではありません。2元合金を考慮する際には、エネルギー障壁\(W\)、フェーズフィールドモビリティ\(M_{\phi}\)も修正する必要があります。
これらは純粋な原子A、Bの量に関して濃度を重みとした線形和となり、次のように与えられます。
W &= \left(1-x_{B}\right)W_{A}+x_{B}W_{B}\\
M_{\phi} &= \left(1-x_{B}\right)M_{\phi,A}+x_{B}M_{\phi,B}\\
\tag{33}
\end{align}
ここで、\(W_{A},W_{B}\)は純粋な原子A、Bのエネルギー障壁、\(M_{\phi,A},M_{\phi,B}\)は純粋な原子A、Bのフェーズフィールドモビリティを表します。
上式を式\((32)\)へ代入すると、
\frac{\partial \phi}{\partial t}&=-M_{\phi}\left[30\left\{ \frac{L_{A}\left(T-T_{m,A}\right)}{T_{m,A}}\left(1-x_{B}\right)+\frac{L_{B}\left(T-T_{m,B}\right)}{T_{m,B}}x_{B}\right\}\phi^2\left(1-\phi\right)^2\right.\\
&\left. \quad\quad\quad+2\left\{\left(1-x_{B}\right)W_{A}+x_{B}W_{B}\right\}\phi (1-\phi)(1-2\phi)\right.\\
&\left. \quad\quad\quad\quad\quad -2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
\right.\\
&\left.\quad\quad\quad\quad\quad\quad
-\frac{\partial }{\partial x}\left( a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial x}
\right)
\right] \\
\rightarrow
\frac{\partial \phi}{\partial t}&=-M_{\phi}\left[\left\{ 30\frac{L_{A}\left(T-T_{m,A}\right)}{T_{m,A}}\phi^2\left(1-\phi\right)^2+2W_{A}\phi (1-\phi)(1-2\phi)\right\}\left(1-x_{B}\right)\right.\\
&\left. \quad\quad\quad+\left\{30\frac{L_{B}\left(T-T_{m,B}\right)}{T_{m,B}}\phi^2\left(1-\phi\right)^2+2W_{B}\phi (1-\phi)(1-2\phi)\right\}x_{B}\right.\\
&\left. \quad\quad\quad\quad\quad -2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
\right.\\
&\left.\quad\quad\quad\quad\quad\quad
-\frac{\partial }{\partial x}\left( a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial x}
\right)
\right] \\
\rightarrow
\frac{\partial \phi}{\partial t}&=-\left[\left(1-x_{B}\right)M_{\phi,A}+x_{B}M_{\phi,B}\right]\left[H_{A}\left(1-x_{B}\right) +H_{B}x_{B}\right.\\
&\left.\quad\quad\quad\quad-2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
\right.\\
&\left.\quad\quad\quad\quad\quad\quad
-\frac{\partial }{\partial x}\left( a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial x}
\right)
\right]
\tag{34}
\end{align}
ここで\(H_{A},H_{B}\)は以下の式で与えられます。
H_{A}= 30\frac{L_{A}\left(T-T_{m,A}\right)}{T_{m,A}}\phi^2\left(1-\phi\right)^2+2W_{A}\phi (1-\phi)(1-2\phi)\\
H_{B}=30\frac{L_{B}\left(T-T_{m,B}\right)}{T_{m,B}}\phi^2\left(1-\phi\right)^2+2W_{B}\phi (1-\phi)(1-2\phi)\\
\tag{35}
\end{align}
以上が2元系合金におけるアレンカーン方程式です。
おわりに
今回は正則溶体近似に関してまとめました。以前、状態図計算の記事でまとめた時より、若干簡略化された定式化になっており、厳密性は欠けますがこちらのほうが分かりいいかもしれません。次回はWBMモデルについてまとめたいと思います。
参考文献
[1] 高木 知弘ら, “フェーズフィールド法”, 養賢堂, 2012/3/2
[2] 山中 晃徳ら, “Pythonによるフェーズフィールド法入門 基礎理論からデータ同化の実装まで”, 丸善出版, 2023/12/15
[3] 小山 敏幸ら, “フェーズフィールド法入門 (計算力学レクチャーコース) “, 丸善出版, 2013/4/13
[4] J.A. Warren, W.J. Boettinger : “Prediction of dendritic growth and microsegregation patterns in a binary alloy using the phase-field method”. Acta Metallurgica et Materialia, Volume 43, Issue 2, February 1995, Pages 689-703



コメント