はじめに
前回記事では、アレンカーン方程式に現れる係数(界面モビリティ\(M_{\phi}\)、エネルギー障壁\(W\)、勾配係数\(a\))と物性値(界面幅\(\delta\)、界面エネルギー\(\gamma\)、界面モビリティ\(M\))の関連付けを行いました。今回は実際に1次元アレン-カーン方程式を解き、各パラメーターが解に与える影響について考察します。
1次元アレン-カーン方程式の離散化
前回記事では、汎関数微分を計算したアレン-カーン方程式は次のように書かれました。
\frac{\partial \phi}{\partial t}&=M_{\phi}\left[a^2\frac{\partial^2 \phi}{\partial x^2} -\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}-W\frac{\partial q(\phi)}{\partial \phi}\right] \tag{1}\\
p(\phi)&=\phi ^2(3-2\phi) \tag{2}\\
q(\phi)&=\phi ^2 (1-\phi)^2 \tag{3} \\
\end{align}
式\((2),(3)\)を用いると、式\((1)\)の各項は次のように計算できます。
\frac{\partial p(\phi)}{\partial \phi} &=\frac{\partial }{\partial \phi} \left[\phi ^2(3-2\phi) \right]\\
&=2\phi (3-2\phi)+\phi ^2(-2)\\
&=6\phi -4\phi^2-2\phi ^2\\
&=6\phi -6\phi^2\\
&=6\phi\left(1-\phi\right) \tag{4}\\
\end{align}
\frac{\partial q(\phi)}{\partial \phi} &=\frac{\partial }{\partial \phi} \left[\phi ^2 (1-\phi)^2 \right]\\
&= 2\phi (1-\phi)^2 -2 \phi ^2 (1-\phi) \\
&= 2\phi (1-\phi)\left[(1-\phi) -\phi \right]\\
&= 2\phi (1-\phi)(1-2\phi) \tag{5}\\
\end{align}
これらを式\((1)\)に代入すると、以下の\(\phi\)に関する方程式を得ることができます。
\frac{\partial \phi}{\partial t}&=M_{\phi}\left[a^2\frac{\partial^2 \phi}{\partial x^2} -6\left(g_{a}-g_{b}\right)\phi\left(1-\phi\right)-2W\phi (1-\phi)(1-2\phi) \right] \tag{6}\\
\end{align}
さらに式\((6)\)を離散化していきます。左辺の時間微分はオイラー陽解法で、右辺の空間2階微分は中心差分法で離散化すると次式が得られます。
&\frac{\phi^{n+1}_{i}-\phi^n_{i}}{\Delta t}=M_{\phi}\left[a^2\frac{\phi^{n}_{i-1}-2\phi^{n}_{i}+\phi^{n}_{i+1}}{\left(\Delta x\right)^2}-6\left(g_{a}-g_{b}\right)\phi ^{n} _{i}\left(1-\phi^{n} _{i}\right)-2W\phi_{i}^{n} (1-\phi_{i}^{n})(1-2\phi_{i}^{n}) \right] \\
&\Leftrightarrow
\phi^{n+1}_{i}=\phi^n_{i}\\
&\quad \quad \quad+{\Delta t}M_{\phi}\left[a^2\frac{\phi^{n}_{i-1}-2\phi^{n}_{i}+\phi^{n}_{i+1}}{\left(\Delta x\right)^2} -6\Delta g\phi ^{n} _{i}\left(1-\phi^{n} _{i}\right)-2W\phi^{n}_{i} (1-\phi^{n}_{i})(1-2\phi^{n}_{i}) \right] \tag{7}\\
\end{align}
ここで\(\Delta g =g_{a}-g_{b}\)としました。以上が1次元アレン-カーン方程式の離散化形式です。
初期条件・境界条件
初期条件として、原点を境に相a(\(\phi=1\))から相b(\(\phi=0\))に連続的に変化する以下のシグモイド関数を設定します。
\phi _0=\frac{1}{1+\exp(2x)}\tag{8}\\
\end{align}
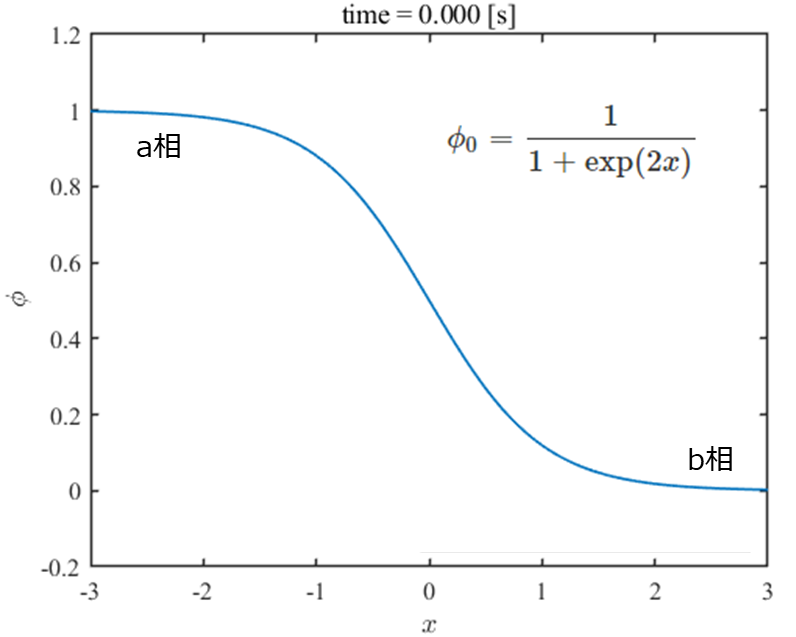
また境界条件は両端で勾配が0になるノイマン条件を設定することとします。
MATLABコード
以下に今回使用したMATLABコードを記載します。
% 初期化処理 ---------------------------------------------------
clc; close all;
clear all;
% パラメーター設定 ---------------------------------------------
dx = 0.05; % 差分格子点の間隔[m]
a = 1; % 勾配エネルギ―係数[(J/m)^1/2]
w = 1; % エネルギー障壁[J/m3]
dg = 1; % 化学的駆動力[J/m3]
mp = 1; % 界面モビリティ[m3/js]
dt = 0.001; % タイムステップ[s]
maxstep = 5000; % 最大ステップ数
xmax = 3;
xmin = -3;
xl = xmin:dx:xmax;
% 変数宣言
nx = size(xl,2);% 差分格子点数
phi = zeros(nx,maxstep);
dphi = zeros(nx,maxstep);
% 安定条件の確認(cが0.5以下でないと不安定)
c = a^2 *dt / dx^2;
% 初期条件 ---------------------------------------------------
for i = 1 : nx
%phi(i,1) = exp(-1 * (xl(i)).^2);% Gaussian wave
phi(i,1) = 1/(1+exp(2*xl(i)));% sigmoid
end
% 時間発展 ---------------------------------------------------
for step = 1 : maxstep - 1
for i = 2 : nx - 1
dphi(i,step) = a^2 * ((phi(i-1,step) -2*phi(i,step) +phi(i+1,step))/dx^2) ...
- 6 * dg * phi(i,step)*(1-phi(i,step)) - w*2*phi(i,step)*(1-phi(i,step))*(1-2*phi(i,step));
% dphi(i,step) = a^2 * ((phi(i-1,step) -2*phi(i,step) +phi(i+1,step))/dx^2) ...
% - 30 * dg *phi(i,step)^2*(phi(i,step)^2-2*phi(i,step)+1) - 2*w*phi(i,step)*(1-phi(i,step))*(1-2*phi(i,step));
phi(i,step + 1) = phi(i,step) + dt * mp * dphi(i,step);
end
% ノイマン境界条件
phi(1,step+1) = phi(2,step+1);
phi(nx,step+1) = phi(nx-1,step+1);
end
% 可視化 ---------------------------------------------------
% VideoWriter オブジェクトの初期化
filename = ['a = ', num2str(a, '%.0f'), ', w = ', num2str(w, '%.0f'), ...
', dg = ', num2str(dg, '%.0f'), ', mp = ', num2str(mp, '%.3f'),'.mp4'];
outputVideo = VideoWriter(filename, 'MPEG-4');
outputVideo.FrameRate = 30; % フレームレートの設定
open(outputVideo);
% グラフィックオブジェクトの初期化と再利用
fig = figure(1);
plotHandle = plot(xl, phi(:,1), 'LineWidth', 1.2); % 初期プロット
xlim([xmin, xmax]);
ylim([-0.2, 1.2]);
xlabel('$$x$$', 'Interpreter', 'latex', 'FontSize', 14);
ylabel('$$\phi$$', 'Interpreter', 'latex', 'FontSize', 14);
ax = gca;
ax.FontName = 'Times New Roman';
ax.FontSize = 12;
ax.LineWidth = 1.2; % 枠の太さ
fig.Color = 'white';
titleHandle = title(sprintf('time = %.3f [s]', 0));
legendHandle = legend(['$a = ', num2str(a, '%.1f'), '\, , W = ', ...
num2str(w, '%.1f'), ', \, \Delta g = ', num2str(dg, '%.1f'), '$'], ...
'Location', 'southeast', 'FontSize', 10, 'Interpreter', 'latex');
% 動画のフレームを記録するためのループ
for step = 1:maxstep
if mod(step, 20) == 0
set(plotHandle, 'YData', phi(:,step)); % データ点の更新
set(titleHandle, 'String', sprintf('time = %.3f [s]', step * dt)); % タイトルの更新
drawnow; % 必要な場合のみ使用
frame = getframe(gcf);
writeVideo(outputVideo, frame);
end
end
% 動画の書き出しを完了
close(outputVideo);
各パラメーターの影響
アレン-カーン方程式\((7)\)のパラメーターとしては界面モビリティ\(M_{\phi}\)、勾配係数\(a\)、エネルギー障壁\(W\)、化学的駆動力(2相の化学的エネルギー密度の差)\(\Delta g\)の4つがあります。
式\((7)\)より\(M_{\phi}\)は右辺第二項全体をスケール倍しています。あるいはタイムステップをスケール倍していると捉えてもよいでしょう。いずれにせよ反応を加減速させる効果を有しているわけです。今回は各項が解にどのように影響を与えるかを確認したいので、ひとまず\(M_{\phi}=1\)としておきます。
はじめに勾配係数\(a\)の影響を見るために、次のようなパラメーターで計算を実行します。
| パラメーター | 値 |
|---|---|
| \(a\) | 1 |
| \(W\) | 0 |
| \(\Delta g\) | 0 |
時間とともに解が鈍っていき、やがて平坦になります。これは拡散方程式の解と同等です。\(W=0,\Delta g=0\)の時、アレン-カーン方程式\((7)\)は、拡散方程式に帰着し、勾配係数\(a\)は拡散係数に相当します。
次にエネルギー障壁\(W\)の影響を見るために、以下のようなパラメーターで計算を実行します。
| パラメーター | 値 |
|---|---|
| \(a\) | 0 |
| \(W\) | 1 |
| \(\Delta g\) | 0 |
この場合、初期状態で緩やかだった解が時間とともにステップ型に変化します。すなわちエネルギー障壁\(W\)は相状態をより明確に分離する効果があります。このことはエネルギー障壁\(W\)が与えるダブルポテンシャル項\(g_{doub}\)(こちらの記事参照)を最小化するように相状態が変化することを示しています。
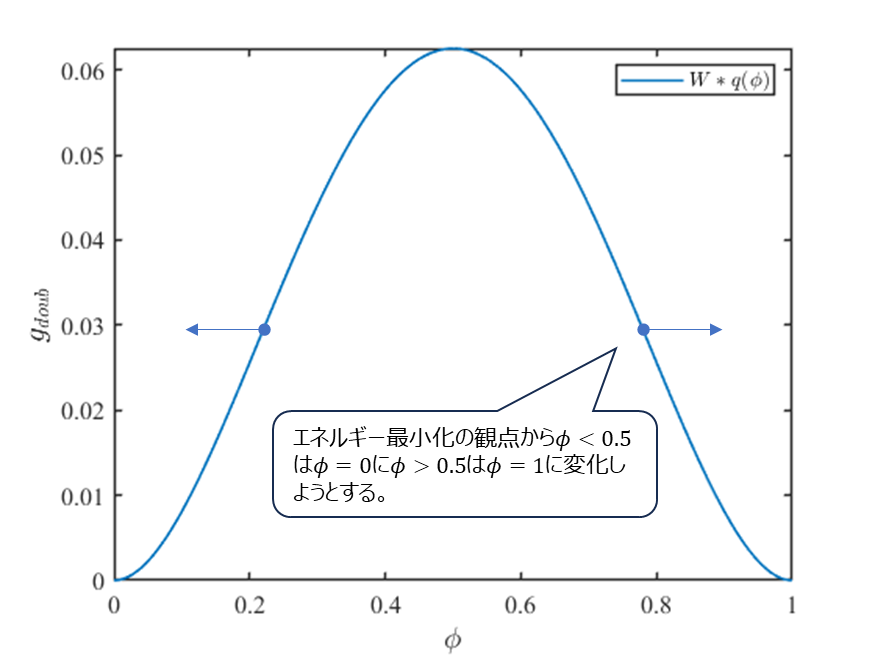
最後に、化学的駆動力\(\Delta g=g_{a}-g_{b}\)の影響を見るために、次のパラメーターで計算を実行します。
| パラメーター | 値 |
|---|---|
| \(a\) | 0 |
| \(W\) | 0 |
| \(\Delta g\) | 1 |
時間とともにb相(\(\phi =0\))の領域が広がっていき、a相(\(\phi =1\))の領域がなくなっていきます。これは\(\Delta g=g_{a}-g_{b}=1>0\)より、a相よりb相のほうがエネルギー的に小さいため、より安定であるb相が成長することを示しています。逆に\(\Delta g=g_{a}-g_{b}<0\)の場合は、a相が成長することとなります。
また、式\((2)\)より、\(\phi=0,1\)において、\(\frac{\partial p(\phi)}{\partial \phi}=0\)になることから、\(\phi=0,1\)の時、化学的自由エネルギー密度の項は、一才の影響をお及ぼさなくなることに注意しましょう。
以上で各項の解への影響が分かりました。実際にはこれらの3つの効果が組み合わさって相状態が計算されます。
エネルギー密度分布関数\(p(\phi)\)についての考察
エネルギー密度分布関数\(p(\phi)\)は式\((2)\)以外にも次のような形をとる場合もありました。(前回記事参照)
p(\phi)&=\phi ^3\left(10-15\phi+6\phi^2\right) \tag{9}\\
\end{align}
式\((2),(9)\)を同時にプロットすると以下の通りです。
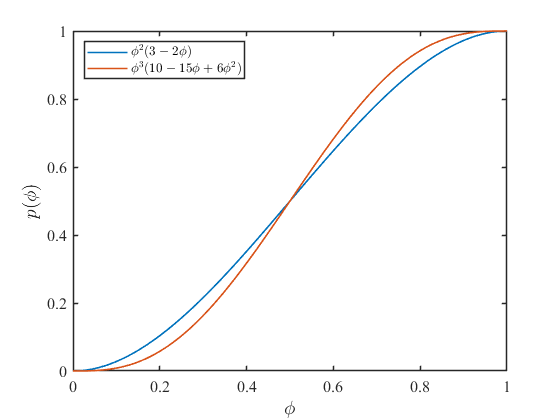
両者のプロファイルはよく似ていますが、解の挙動に与える影響は少々異なるようです。式\((9)\)が成り立つ場合、式\((5)\)は以下のように変化します。
\frac{\partial p(\phi)}{\partial \phi} &=\frac{\partial }{\partial \phi} \left[\phi ^3\left(10-15\phi+6\phi^2\right)\right]\\
&=30 \phi^2 -60 \phi^3+30\phi ^4 \\
&=30 \phi^2\left( 1-2\phi+\phi^2\right) \\
&= 30\phi^2 (\phi-1)^2 \tag{10}\\
\end{align}
アレン-カーン方程式\((1)\)の中では、\(p(\phi)\)の一回微分\(\frac{\partial p(\phi)}{\partial \phi}\)の大きさが、化学的駆動力\((g_{a}-g_{b})\)の影響の度合いを決めていました。\(\frac{\partial p(\phi)}{\partial \phi}\)について二種の\(p(\phi)\)を比較してみると次のようなグラフが得られます。
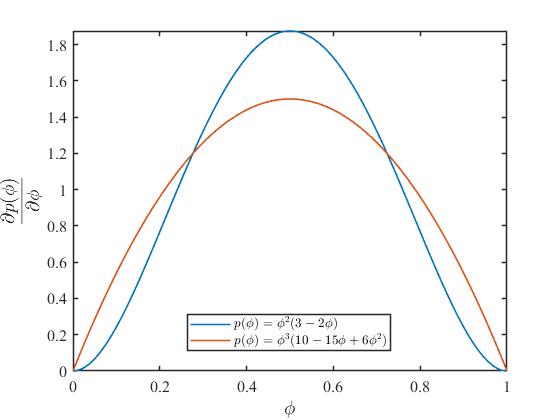
すなわち、式\((9)\)は式\((2)\)と比較すると、\(\phi\sim0.5\)といったピーク領域では化学的駆動力\((g_{a}-g_{b})\)の影響を強め、\(\phi=0\sim0.3,0.7\sim 1\)といった裾野部分では化学的駆動力の影響を弱める効果があると言えます。このことは解の挙動にどういった影響を及ぼすでしょうか?実際に計算して確かめてみます。
エネルギー密度分布関数\(p(\phi)\)として式\((9)\)を採用する場合、アレン-カーン式\((6)\)は以下のように変化します。
\frac{\partial \phi}{\partial t}&=M_{\phi}\left[a^2\frac{\partial^2 \phi}{\partial x^2} -30\left(g_{a}-g_{b}\right)\phi^2\left(1-\phi\right)^2-2W\phi (1-\phi)(1-2\phi) \right] \tag{11}\\
\end{align}
これを離散化すると最終的には次式が得られます。
\phi^{n+1}_{i}=\phi^n_{i}+{\Delta t}M_{\phi}\left[a^2\frac{\phi^{n}_{i-1}-2\phi^{n}_{i}+\phi^{n}_{i+1}}{\left(\Delta x\right)^2} -30\Delta g\left(\phi ^{n} _{i}\right)^2\left(1-\phi^{n} _{i}\right)^2-2W\phi^{n}_{i} (1-\phi^{n}_{i})(1-2\phi^{n}_{i}) \right]
\tag{12}
\end{align}
上式について、化学的駆動力\(\Delta g=g_{a}-g_{b}\)の影響を見るために、次のパラメーターで計算を実行します。
| パラメーター | 値 |
|---|---|
| \(a\) | 0 |
| \(W\) | 0 |
| \(\Delta g\) | 1 |
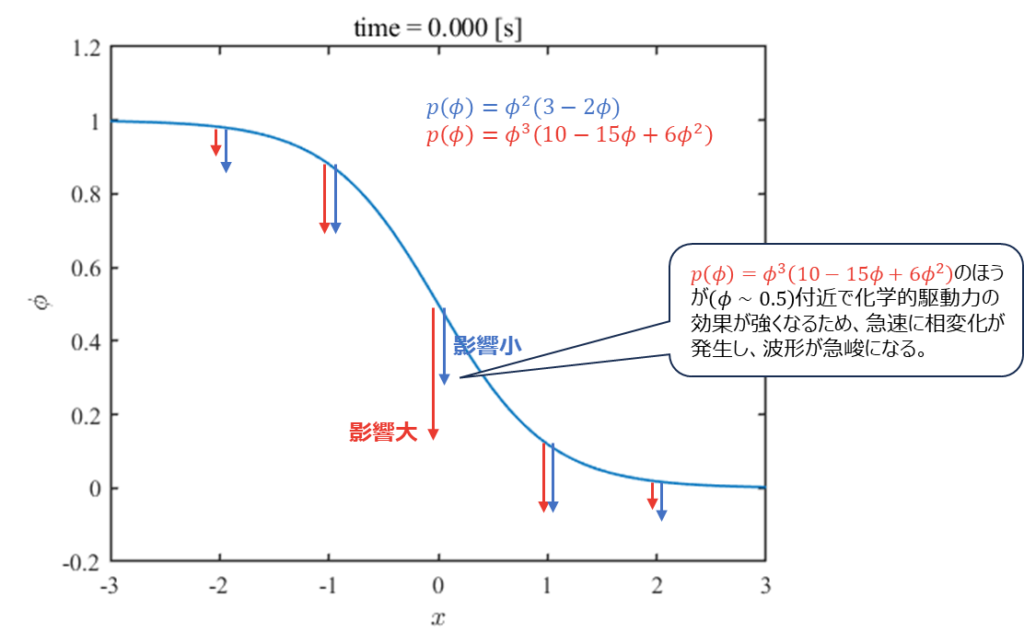
\(p(\phi)\)として式\((2)\)を採用する場合、前節に見られたように比較的早い段階で、b相(\(\phi=0\))が優勢になりましたが、式\((9)\)を採用した場合、b相(\(\phi=0\))がa相(\(\phi=1\))を侵食しながら、急激にカーブが急峻になり、急峻になった後は比較的ゆっくりとb相が進展してきます。すなわち、式\((9)\)の場合、単純にエネルギーが低い相を進展させる効果だけでなく、「両相を明確に分離・安定化させ、その後の相変化をゆっくりにする」という効果が顕著に現れます。両相を分離する効果はダブルウェルポテンシャルに似ています。
このような効果は式\((9)\)のほうが式\((2)\)より\(\phi\sim0.5\)付近で化学的駆動力の効果が強くなるため、急速にb相(\(\phi=0\))に変化し、その結果、波形が急峻になることで発生していると考えられます。急峻なピークが形成されると、\(\phi=0,1\)近傍において\(\frac{\partial p(\phi)}{\partial \phi}\sim 0\)であるため、化学的駆動力の効果は減衰し、相変化は緩やかになります。
このようなモデル化が実際の組織変化をより精密に再現しているのかは分かりませんが、式\((9)\)のほうが相分離が早まり、早い段階で計算が安定化するようです。参考文献を見る限り、エネルギー密度分布関数\(p(\phi)\)として式\((2)\)と式\((9)\)のどちらを採用するかは、問題によって切り替えられています。個人的には式\((2)\)のほうが、よりシンプルな効果を与えているので分かりやすいと思うのですが…。
おわりに
今回は1次元アレン-カーン方程式を解き、各項が与える影響についてまとめました。ギブスの自由エネルギーのモデル化に応じて各項が違った寄与を見せるのが興味深いです。次回は2次元でアレン-カーン方程式を解いてみたいと思います。
参考文献
[1] 高木 知弘ら, “フェーズフィールド法”, 養賢堂, 2012/3/2
[2] 山中 晃徳ら, “Pythonによるフェーズフィールド法入門 基礎理論からデータ同化の実装まで”, 丸善出版, 2023/12/15



コメント