はじめに
前回は1次元非粘性Bugers方程式について、1次精度の空間離散化とRoeリーマンソルバを用いて計算しました。今回はさらに高次精度の空間離散化方法についてまとめます。
有限体積法における空間高次精度化
前回記事では、セル\(i\)に属する界面物理量\({}^R\! q_{i-\frac{1}{2}},{}^L\! q_{i+\frac{1}{2}}\)を次のように書けることを示しました。
{}^R\! q_{i-\frac{1}{2}}=\bar{\cal{q}}_{i}
-\frac{1}{2}Q_{i}'(x_{i-\frac{1}{2}})\Delta x_{i}
-\frac{1}{6}Q_{i}^{\prime\prime}(x_{i-\frac{1}{2}})\Delta x_{i}^2
+O\left(\Delta x_{i}^3\right)\tag{1}\\
{}^L\! q_{i+\frac{1}{2}}=\bar{\cal{q}}_{i}
-\frac{1}{2}Q_{i}'(x_{i+\frac{1}{2}})\Delta x_{i}
-\frac{1}{6}Q_{i}^{\prime\prime}(x_{i+\frac{1}{2}})\Delta x_{i}^2
+O\left(\Delta x_{i}^3\right)\tag{2}
\end{align}
この時、空間1次精度での離散化とし、補間関数の微分項\(Q_{i}'(x_{i-\frac{1}{2}}),Q^{\prime\prime}(x_{i-\frac{1}{2}})\)は無視して計算しましたが、今回はこれらを考慮することで\({}^R\! q_{i-\frac{1}{2}},{}^L\! q_{i+\frac{1}{2}}\)を高次精度化します。
差分法の高次精度化は支配方程式上の微分項の離散化についてテイラー展開の次数を上げていくことを指しましたが、有限体積法の高次精度化はこのように界面物理量の次数を上げることで数値流束の精度を上げることを指すようです。
では補間関数\(Q_{i}(x)\)の微分項はどのように表現されるのでしょうか?単純に考えるなら離散変数\(\bar{\cal{q}}_{i}\)を用いて、\(Q_{i}'(x_{i+\frac{1}{2}})=\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}{\Delta x_{i}}\)などと表したくなりますが果たしてこれが正しいものか…。
はたまた以下のように補間関数\(Q_{i}(x)\)を\(x_{i}\)の周りでテイラー展開して、それを微分する方法はどうでしょうか?
Q_i(x)&=Q_i(x_{i})+Q'(x_{i})(x-x_{i})+\frac{1}{2}Q^{\prime\prime}(x_{i})(x-x_{i})^2+\frac{1}{6}Q^{\prime\prime\prime}(x_{i})(x-x_{i})^3+O((x-x_{i})^4)\\
\tag{3}
\end{align}
ただしこの場合、結局右辺に\(Q_{i}(x)\)の微分項が存在してしまいます。この辺りを数理的に決めていきたいところです。
補間関数の多項式近似
素直にテイラー展開することはできないと分かったので、ひとまずテイラー展開における係数を未知の定数\(c_{m}(m=0,1,2,\cdots,M)\)としておき、\(Q_i(x)\)を以下の\(M\)次多項式にて近似することを考えます。
Q_i(x)&=\sideset{}{}{\sum}_{m=0}^{M}c_{m}(x-x_{i})^m+O((x-x_{i})^{M+1})\\
\tag{4}
\end{align}
この係数\(c_{m}\)を決めることが出来れば、式\((4)\)を微分することで式\((1),(2)\)中に現れる微分項を得ることも可能でしょう。(あるいは\(Q_{i}(x)\)が決まれば\({}^L\! q_{i+\frac{1}{2}}=Q_i(x_{i+\frac{1}{2}}),{}^R\! q_{i+\frac{1}{2}}=Q_{i+1}(x_{i+\frac{1}{2}})\)の関係から界面物理量を決めることも可能です。)
では実際に係数\(c_{m}\)を求めていきます。仮に\(Q_{i}(x)\)を空間3次精度まで考えるとすると式\((4)\)は\(M=2\)として以下のように書けます。
Q_i(x)&=c_{0}+c_{1}(x-x_{i})+c_{2}(x-x_{i})^2+O((x-x_{i})^{3})\\
\tag{5}
\end{align}
式\((5)\)は未知数が3つ(\(c_{0},c_{1},c_{2}\))なので、これらを決めるのには式\((5)\)以外に3つの式が必要です。そこで3つのステンシル\(\bar{\cal{q}}_{i-1},\bar{\cal{q}}_{i},\bar{\cal{q}}_{i+1}\)を用いて、以下の制約条件を課します。
&\bar{\cal{q}}_{i-1}=\frac{1}{\Delta x_{i-1}}\int_{i-\frac{3}{2}}^{i-\frac{1}{2}}Q_{i}(x)dx \tag{6}\\
&\bar{\cal{q}}_{i}=\frac{1}{\Delta x_i}\int_{i-\frac{1}{2}}^{i+\frac{1}{2}}Q_{i}(x)dx \tag{7}\\
&\bar{\cal{q}}_{i+1}=\frac{1}{\Delta x_{i+1}}\int_{i+\frac{1}{2}}^{i+\frac{3}{2}}Q_{i}(x)dx \tag{8}
\end{align}
ここで式\((7)\)は補完関数の定義そのものなのでよいとしても、式\((6),(8)\)は違和感を持つかもしれません。補間関数の定義から言えば式\((6),(8)\)は被積分関数を\(Q_{i-1},Q_{i+1}\)として以下のように書かれるのが正しいように思えます。
\bar{\cal{q}}_{i-1}=\frac{1}{\Delta x_{i-1}}\int_{i-\frac{3}{2}}^{i-\frac{1}{2}}Q_{i-1}(x)dx \tag{9}\\
\bar{\cal{q}}_{i+1}=\frac{1}{\Delta x_{i+1}}\int_{i+\frac{1}{2}}^{i+\frac{3}{2}}Q_{i+1}(x)dx \tag{10}
\end{align}
しかしながら、実際には式\((6),(8)\)も式\((9),(10)\)も特に誤りではありません。イメージ的には「式\((6),(8)\)を用いることで\(Q_{i}(x)\)をセル\(i\)だけでなく、隣接セル\(i-1,i+1\)における離散変数\(\bar{\cal{q}}_{i-1},\bar{\cal{q}}_{i+1}\)も再現可能な補間関数として構築し、精度を上げる。」という考え方になります。そもそも式\((5)\)は\(Q_{i}(x)\)に関する式なので、式\((9),(10)\)は\(c_{0},c_{1},c_{2}\)を決める制約条件にはなり得ません。
式\((6)\sim(8)\)を用いると\(c_{0},c_{1},c_{2}\)は以下のように書けます。
&c_{0}= \bar{\cal{q}}_{i}-\frac{1}{24}\left( \bar{\cal{q}}_{i+1}-2\bar{\cal{q}}_{i}+\bar{\cal{q}}_{i-1}\right) = \bar{\cal{q}}_{i}-\frac{1}{24}\delta _{i}^2 q \tag{11}\\
&c_{1}=\frac{1}{2}\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i-1}}{\Delta x}=\frac{\delta _{i}q}{\Delta x}\tag{12}\\
&c_{2}=\frac{1}{2}\frac{\bar{\cal{q}}_{i+1}-2\bar{\cal{q}}_{i}+\bar{\cal{q}}_{i-1}}{\Delta x^2}=\frac{1}{2}\frac{\delta _{i}^2 q}{\Delta x^2}\tag{13}\\
\end{align}
簡単のため、\(\Delta x = \Delta x_{i-1}= \Delta x_{i} = \Delta x_{i+1} \)として考えます。まず式\((7)\)に式\((5)\)を代入して、積分を実行します。
\bar{\cal{q}}_{i}=\frac{1}{\Delta x}\int_{i-\frac{1}{2}}^{i+\frac{1}{2}}c_{0}+c_{1}(x-x_{i})+c_{2}(x-x_{i})^2+O((x-x_{i})^{3})dx \tag{A1}
\end{align}
ここで\(A=x-x_{i}\)と置いて置換積分を行います。積分範囲は以下のように変化します。
| \(x\) | \(x_{i-\frac{1}{2}} \rightarrow x_{i+\frac{1}{2}}\) |
| \(A\) | \(x_{i-\frac{1}{2}} -x_{i}=-\frac{\Delta x}{2}\rightarrow x_{i+\frac{1}{2}} -x_{i}=\frac{\Delta x}{2}\) |
従って、式\((A1)\)は以下のように書けます。
\bar{\cal{q}}_{i}&=\frac{1}{\Delta x}\int_{-\frac{\Delta x}{2}}^{\frac{\Delta x}{2}}c_{0}+c_{1}A+c_{2}A^2+O(A^{3})dx \\
&=\frac{1}{\Delta x}\left[c_{0}A+\frac{1}{2}c_{1}A^2+\frac{1}{3}c_{2}A^3+O(A^{4})\right]_{-\frac{\Delta x}{2}}^{\frac{\Delta x}{2}} \\
&=\frac{1}{\Delta x}\left[c_{0}A+\frac{1}{3}c_{2}A^3\right]_{-\frac{\Delta x}{2}}^{\frac{\Delta x}{2}} \\
&=c_{0}+\frac{1}{12}c_{2}\Delta x^2 \tag{A2}
\end{align}
同様に式\((6)\)に式\((5)\)を代入して、積分を実行します。
\bar{\cal{q}}_{i-1}&=\frac{1}{\Delta x}\int_{i-\frac{3}{2}}^{i-\frac{1}{2}}c_{0}+c_{1}(x-x_{i})+c_{2}(x-x_{i})^2+O((x-x_{i})^{3})dx\\
&=\frac{1}{\Delta x}\int_{-\frac{3\Delta x}{2}}^{-\frac{\Delta x}{2}}c_{0}+c_{1}A+c_{2}A^2+O(A^{3})dA\\
&=\frac{1}{\Delta x}\left[ c_{0}A+\frac{1}{2}c_{1}A^2+\frac{1}{3}c_{2}A^3+O(A^{4})\right]_{-\frac{3\Delta x}{2}}^{-\frac{\Delta x}{2}}\\
&=c_{0}-c_{1}\Delta x+\frac{13}{12}c_{2}\Delta x^2+O(\Delta x^{3})\tag{A3}
\end{align}
また式\((8)\)に式\((5)\)を代入すると、
\bar{\cal{q}}_{i+1}&=\frac{1}{\Delta x}\int_{i+\frac{1}{2}}^{i+\frac{3}{2}}c_{0}+c_{1}(x-x_{i})+c_{2}(x-x_{i})^2+O((x-x_{i})^{3})dx\\
&=\frac{1}{\Delta x}\int_{\frac{\Delta x}{2}}^{\frac{3\Delta x}{2}}c_{0}+c_{1}A+c_{2}A^2+O(A^{3})dx \\
&=\frac{1}{\Delta x}\left[ c_{0}A+\frac{1}{2}c_{1}A^2+\frac{1}{3}c_{2}A^3+O(A^{4})\right]_{\frac{\Delta x}{2}}^{\frac{3\Delta x}{2}} \\
&= c_{0}+c_{1}\Delta x+\frac{13}{12}c_{2}\Delta x ^2+O(\Delta x^{3})\tag{A4}
\end{align}
ここまでの結果をまとめると以下の通りです。
\bar{\cal{q}}_{i}&=c_{0}+\frac{1}{12}c_{2}\Delta x^2 \tag{A2}\\
\bar{\cal{q}}_{i-1}&=c_{0}-c_{1}\Delta x+\frac{13}{12}c_{2}\Delta x^2+O(\Delta x^{3})\tag{A3}\\
\bar{\cal{q}}_{i+1}&=c_{0}+c_{1}\Delta x+\frac{13}{12}c_{2}\Delta x ^2+O(\Delta x^{3})\tag{A4}
\end{align}
以上、式\((A2)\sim(A5)\)を用いて\(c_{1},c_{2},c_{3}\)について連立方程式を解くことで、式\((11)\sim (13)\)を得ることが出来ます。
ここで\(\delta _{i}q = \frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i-1}}{2},\delta _{i}^2 q=\bar{\cal{q}}_{i+1}-2\bar{\cal{q}}_{i}+\bar{\cal{q}}_{i-1}\)と置いています。また簡単のため、\(\Delta x = \Delta x_{i-1}= \Delta x_{i} = \Delta x_{i+1} \)としました。
上式より\(c_{1} \sim \left(\frac{\partial q}{\partial x}\right)_{i},c_{2}\sim \frac{1}{2}\left(\frac{\partial^2 q}{\partial x^2}\right)_{i}\)となり中心差分法を用いたテイラー展開の形になっていることが分かります。また\(c_{0}\)に含まれる\(-\frac{1}{24}\delta _{i}^2 q \)は3次精度の補間により発生する定数項です。
式\((11)\sim (13)\)を式\((5)\)に代入すると以下の式が得られます。
Q_i(x)&=\left( \bar{\cal{q}}_{i}-\frac{1}{24}\delta _{i}^2 q \right)+\frac{\delta _{i}q }{\Delta x}(x-x_{i})+\left(\frac{1}{2}\frac{\delta _{i}^2 q}{\Delta x^2} \right)(x-x_{i})^2+O((x-x_{i})^{3})\\
&=\bar{\cal{q}}_{i}+\frac{\delta _{i}q }{\Delta x}(x-x_{i})+\frac{1}{2\Delta x^2}\left( (x-x_{i})^2 -\frac{\Delta x^2}{12}\right)\delta _{i}^2 q+O((x-x_{i})^{3})\\
\tag{14}
\end{align}
また\(Q_{i}(x)\)はセル\(i\)の補間関数なので\(x\)が\(x_{i}\)近傍の値をとると考えると、\(x-x_{i} \sim \Delta x\)と書けます。したがって誤差項も\(O_{i}((x-x_{i})^3) \sim O(\Delta x^3)\)と書き替えることが出来ます。
Q_i(x)&=\bar{\cal{q}}_{i}+\frac{\delta _{i}q }{\Delta x}(x-x_{i})+\frac{1}{2\Delta x^2}\left( (x-x_{i})^2 -\frac{\Delta x^2}{12}\right)\delta _{i}^2 q+O(\Delta x^{3})\\
\tag{15}
\end{align}
上式が補間関数\(Q_{i}\)の多項式近似による表現です。今回は係数\(c_{m}\)を3つのステンシル(\(\bar{\cal{q}}_{i-1},\bar{\cal{q}}_{i},\bar{\cal{q}}_{i+1}\))を用いて表現したので「3セル2次補間」となり、空間3次精度です。また、詳しくは後述しますが2つのステンシルを用いる場合は、「2セル線形補間」となり空間2次精度となります。2セル線形補間を用いた場合、上式\((15)\)の第二項まで考慮したことに相当します。
さらに上式は以下のように一般化した形で表すことが出来ます。
Q_i(x)&=\bar{\cal{q}}_{i}+ \epsilon\left[\frac{\delta _{i}q }{\Delta x}(x-x_{i})+\frac{3\kappa}{2\Delta x^2}\left( (x-x_{i})^2 -\frac{\Delta x^2}{12}\right)\delta _{i}^2 q\right]+O(\Delta x^{3})\\
\tag{16}
\end{align}
この一般化は少々唐突に思えますが、1次精度(第一項)に対する補正量(第二項以降)の調整の仕方で、空間精度が変化することを意味しています。
例えば\(\epsilon=0\)の場合、第二項以降は消えるので\(Q_i(x)\)は1次精度となります。また\(\epsilon=1, \kappa=\frac{1}{3}\)の場合、式\((16)\)は式\((15)\)に一致するので3次精度になります。
一方、\(\epsilon=1, \kappa \neq \frac{1}{3}\)の場合、第三項が変形し式\((16)\)はぴったり式\((15)\)に一致しなくなります。例えば\(\epsilon= \kappa =1\)の場合、以下のように書けます。
Q_i(x)&=\bar{\cal{q}}_{i}+\frac{\delta _{i}q }{\Delta x}(x-x_{i})+\frac{3}{2\Delta x^2}\left( (x-x_{i})^2 -\frac{\Delta x^2}{12}\right)\delta _{i}^2 q+O(\Delta x^{3})\\
&\sim \bar{\cal{q}}_{i}+\frac{\delta _{i}q }{\Delta x}(x-x_{i})+O(\Delta x^{2})\tag{17}
\end{align}
この場合、後述の通り、第二項目までは2セル線形補間の形と同様な形をしているので式\((17)\)は2次精度になります。とはいえ第三項には\(x\)の二乗項が残っているので補間関数としては2次関数です。このため、一見、3次精度を有しているように見えてしまいますが、実際は2次精度の範囲でしか近似が成立していないことに注意しましょう。
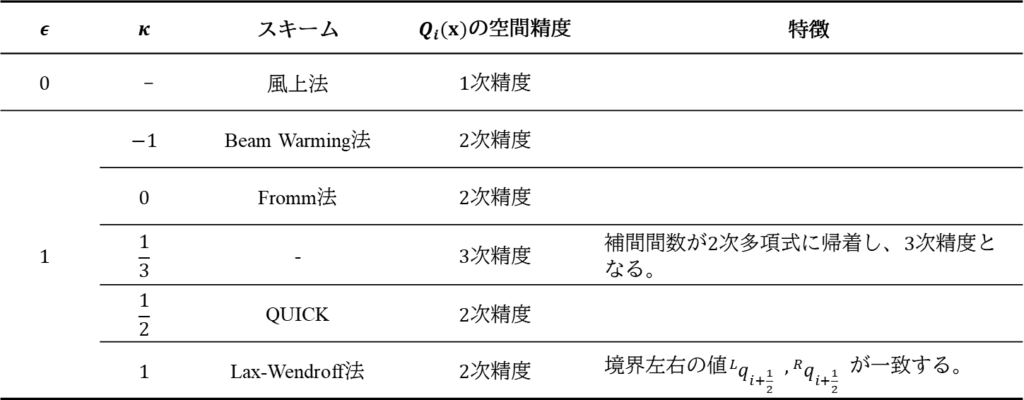
以上のようにパラメーター\( \epsilon,\kappa\)を変えることで様々な精度の補間関数を得ることが出来ます。補間関数の違いは界面物理量、ひいては数値流束の違いとなるため最終的には適用される離散化スキームそのものが\( \epsilon,\kappa\)によって変化することになります。パラメーター、スキーム、精度の関係をまとめると以下の通りです。
最後に式\((16)\)を用いて\(Q_{i}\)の空間微分を計算します。
Q’_{i}(x)&=\epsilon\left(\frac{\delta _{i}q }{\Delta x}+\frac{3\kappa}{\Delta x^2}(x-x_{i})\delta _{i}^2 q\right)+O(\Delta x^{2})\tag{18} \\
Q_{i}^{\prime\prime}(x)&=\frac{3\epsilon\kappa}{\Delta x^2}\delta _{i}^2 q+O(\Delta x)\tag{19}
\end{align}
誤差項はもともと\( O(x-x_{i})\sim O(\Delta x)\)と書き換えを行っていたので、微分すると次数が落ちることに注意しましょう。
界面物理量の高次精度化
式\((18),(19)\)より補間関数の微分量\(Q_{i}'(x),Q_{i}^{\prime\prime}(x)\)が得られたので、これらを式\((1),(2)\)に代入することで、界面物理量を高次精度化します。
まずは\({}^R\! q_{i-\frac{1}{2}}\)から求めます。簡単のため、\(\Delta x = \Delta x_{i-1}= \Delta x_{i} = \Delta x_{i+1} \)として計算します。
{}^R\! q_{i-\frac{1}{2}}&=\bar{\cal{q}}_{i}
-\frac{1}{2}\left[\epsilon\left(\frac{\delta _{i}q }{\Delta x}+\frac{3\kappa}{\Delta x^2}(x_{i-\frac{1}{2}}-x_{i})\delta _{i}^2 q\right)+O(\Delta x^{2}) \right]\Delta x
-\frac{1}{6}\left(\frac{3\epsilon\kappa}{\Delta x^2}\delta _{i}^2 q+O(\Delta x)\right)\Delta x^2
+O\left(\Delta x^3\right)\\
&=\bar{\cal{q}}_{i}
+\epsilon\left[-\frac{\delta _{i}q}{2} -\frac{3\kappa}{2\Delta x}(x_{i-\frac{1}{2}}-x_{i})\delta _{i}^2 q
-\frac{\kappa}{2}\delta _{i}^2 q\right]
+O\left(\Delta x^3\right)
\tag{20}\\
\end{align}
ここで\(x_{i-\frac{1}{2}}-x_{i}=-\frac{\Delta x}{2}\)と置き換えます。
{}^R\! q_{i-\frac{1}{2}}&=\bar{\cal{q}}_{i}
+\epsilon\left(-\frac{\delta _{i}q}{2} +\frac{3\kappa}{2\Delta x}\frac{\Delta x}{2}\delta _{i}^2 q
-\frac{\kappa}{2}\delta _{i}^2 q\right)
+O\left(\Delta x^3\right)\\
&=\bar{\cal{q}}_{i}
+\epsilon\left(-\frac{\delta _{i}q}{2} +\frac{3\kappa}{4}\delta _{i}^2 q
-\frac{\kappa}{2}\delta _{i}^2 q\right)
+O\left(\Delta x^3\right)\\
&=\bar{\cal{q}}_{i}
-\epsilon\left(\frac{\delta _{i}q}{2} -\frac{\kappa}{4}\delta _{i}^2 q
\right)
+O\left(\Delta x^3\right)
\tag{21}\\
\end{align}
2次以上の高次精度を考えるため\(\epsilon = 1\)とおくと
{}^R\! q_{i-\frac{1}{2}}&=\bar{\cal{q}}_{i}
-\frac{\delta _{i}q}{2} +\frac{\kappa}{4}\delta _{i}^2 q+O\left(\Delta x^3\right)\\
&=\bar{\cal{q}}_{i}
-\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i-1}}{4} +\frac{\kappa\left(\bar{\cal{q}}_{i+1}-2\bar{\cal{q}}_{i}+\bar{\cal{q}}_{i-1}\right)}{4}+O\left(\Delta x^3\right)\\
&=\bar{\cal{q}}_{i}
-\left[\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1})+\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i})+O\left(\Delta x^3\right)\right]
\tag{22}
\end{align}
以上が\({}^R\! q_{i-\frac{1}{2}}\)の高次精度表示です。
\({}^L\! q_{i+\frac{1}{2}}\)についても同様に求めると以下のように書くことが出来ます。
{}^L\! q_{i+\frac{1}{2}}=\bar{\cal{q}}_{i}
+\left[\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1})+\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i})+O\left(\Delta x^3\right)\right]
\tag{23}
\end{align}
また、\({}^R\! q_{i+\frac{1}{2}}\)を求める場合、式\((22)\)において\(i \rightarrow i+1\)と置けばよいので以下の通り書けます。
{}^R\! q_{i+\frac{1}{2}}=\bar{\cal{q}}_{i+1}
-\left[\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i})+\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1})+O\left(\Delta x^3\right)\right]
\tag{24}
\end{align}
ここで式\((23),(24)\)について2次精度以上に相当する第二項以降を\(\delta q_{i+\frac{1}{2}}\)とおき、1次精度である第一項と明示的に分離するために以下のように書きます。
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+{}^L\delta q_{i+\frac{1}{2}}\tag{25}\\
{}^R\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i+1}-{}^R\delta q_{i+\frac{1}{2}}\tag{26}
\end{align}
\({}^L\delta q_{i+\frac{1}{2}},{}^R\delta q_{i+\frac{1}{2}}\)と\(\epsilon ,\kappa\)の関係をまとめると下表のようになります。

上表より、BeamWarming法、Fromm法、Lax-Wendroff法は3セル2次補間で近似したにも関わらず、2つのステンシルから構成されており、結果的に2セル線形補間(二次精度)になっていることが分かります。
また、Fromm法はBeamWarming法、Lax-Wendroff法の平均として表されます。これは高次補正量\({}^R\! \delta q_{i+\frac{1}{2}},{}^L\! \delta q_{i+\frac{1}{2}}\)の勾配計算にBeam-Waring法は風上勾配、Lax-Wendroff法は風下勾配、Fromm法は中心勾配を用いてるためです。(後述)
さらに特異?なのはQUICK法です。QUICK法は\(\kappa\neq\frac{1}{3}\)であるため2次精度ですが、3つのステンシルから構成(=3セル2次補間)されています。したがって、式\((6)\sim(8)\)の制約は満たさないものの、補間関数として2次関数を利用する手法なのでしょう。(文献によってはQUICK法は空間3次精度と書いてあったりするので、定式化によって解釈が変わるのかもしれません。ここではあまり深入りしないでおきます。)
以上で高次精度の界面物理量が一通り求まりました。あとは前回記事同様、Roeリーマンソルバにこれらを代入することで数値流束を計算することができます。
高次補正量の勾配計算
表2において、各スキームにおける高次補正量\({}^R\! \delta q_{i+\frac{1}{2}},{}^L\! \delta q_{i+\frac{1}{2}}\)の具体的な表式を示しました。より直感的な理解を得るため、BeamWarming法、Fromm法、Lax-Wendroff法の高次補正量について模式的にグラフ化してみましょう。
まずはBeamWarming法についてです。表2よりBeamWarming法における界面物理量\({}^L\! q_{i+\frac{1}{2}},{}^R\! q_{i+\frac{1}{2}}\)は次式にて表されました。
{}^L\! q_{i+\frac{1}{2}}
&=\bar{\cal{q}}_{i}+{}^L\! \delta q_{i+\frac{1}{2}}
=\bar{\cal{q}}_{i}+\frac{1}{2}\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)\tag{27}\\
{}^R\! q_{i+\frac{1}{2}}
&=\bar{\cal{q}}_{i+1}-{}^R\! \delta q_{i+\frac{1}{2}}
=\bar{\cal{q}}_{i+1}-\frac{1}{2}\left(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1}\right)\tag{28}
\end{align}
これらは次のように変形するとイメージが掴みやすくなります。
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+\frac{\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)}{\Delta x}\frac{\Delta x}{2}\tag{29}\\
{}^R\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i+1}-\frac{\left(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1}\right)}{\Delta x}\frac{\Delta x}{2}\tag{30}
\end{align}
上式は「\(\bar{\cal{q}}_{i}\left(\bar{\cal{q}}_{i+1}\right)\)から傾き\(\frac{\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)}{\Delta x}\left(-\frac{\left(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1}\right)}{\Delta x}\right)\)で\(\frac{\Delta x}{2}\)だけ離れた界面\(i+\frac{1}{2}\)での界面物理量\({}^L\! q_{i+\frac{1}{2}}({}^R\! q_{i+\frac{1}{2}})\)を計算する。」ということを意味しています。これをグラフ化すると次のように書けます。

グラフより界面\(i+\frac{1}{2}\)を風下側と規定すると、\({}^L\! q_{i+\frac{1}{2}}\)(\({}^R\! q_{i+\frac{1}{2}}\))は式\((29)\)(式\((30)\))の右辺第一項\(\bar{\cal{q}}_{i}\)(\(\bar{\cal{q}}_{i+1}\))を基準に風上側のセル平均値を用いて構成されていることが分かります。つまり、BeamWarming法は高次補正量の勾配計算に風上勾配を用いる手法と言えます。
同様にFromm法についても考えます。表2よりBeamWarming法における界面物理量\({}^L\! q_{i+\frac{1}{2}},{}^R\! q_{i+\frac{1}{2}}\)は次式にて表されました。
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+{}^L\! \delta q_{i+\frac{1}{2}}\\
&=\bar{\cal{q}}_{i}+\frac{1}{4}\left(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i-1}\right)\\
&=\bar{\cal{q}}_{i}+\frac{\left(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i-1}\right)}{2\Delta x}\frac{\Delta x}{2}
\tag{31}\\
{}^R\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i+1}-{}^R\! \delta q_{i+\frac{1}{2}}\\
&=\bar{\cal{q}}_{i+1}-\frac{1}{4}\left(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1}\right)\\
&=\bar{\cal{q}}_{i+1}-\frac{\left(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1}\right)}{2\Delta x}\frac{\Delta x}{2}
\tag{32}
\end{align}
グラフ化すると次のように書けます。図が少々複雑なので\({}^L\! q_{i+\frac{1}{2}},{}^R\! q_{i+\frac{1}{2}}\)を別のグラフとして記載します。


グラフより界面\(i+\frac{1}{2}\)を風下側と規定すると、\({}^L\! q_{i+\frac{1}{2}}\)(\({}^R\! q_{i+\frac{1}{2}}\))は式\((29)\)(式\((30)\))の右辺第一項\(\bar{\cal{q}}_{i}\)(\(\bar{\cal{q}}_{i+1}\))を基準に風上側・風下側の両方のセル平均値を用いて構成されていることが分かります。つまり、Fromm法は高次補正量の勾配計算に中心勾配を用いる手法と言えます。
最後にLax-Wendroff法についても考えます。表2よりLax-Wendroff法における界面物理量\({}^L\! q_{i+\frac{1}{2}},{}^R\! q_{i+\frac{1}{2}}\)は次式にて表されました。
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+{}^L\! \delta q_{i+\frac{1}{2}}\\
&=\bar{\cal{q}}_{i}+\frac{1}{2}\left(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}\right)\\
&=\bar{\cal{q}}_{i}+\frac{\left(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}\right)}{\Delta x}\frac{\Delta x}{2}
\tag{33}\\
{}^R\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i+1}-{}^R\! \delta q_{i+\frac{1}{2}}\\
&=\bar{\cal{q}}_{i+1}-\frac{1}{2}\left(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}\right)\\
&=\bar{\cal{q}}_{i+1}-\frac{\left(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}\right)}{\Delta x}\frac{\Delta x}{2}
\tag{34}
\end{align}
グラフ化すると次のように書けます。

グラフより界面\(i+\frac{1}{2}\)を風下側と規定すると、式\((29)\)(式\((30)\))の右辺第一項\(\bar{\cal{q}}_{i}\)(\(\bar{\cal{q}}_{i+1}\))を基準に\({}^L\! q_{i+\frac{1}{2}}\)(\({}^R\! q_{i+\frac{1}{2}}\))は風下側のセル平均値を用いて構成されていることが分かります。つまり、Lax-Wendroff法は高次補正量の勾配計算に風下勾配を用いる手法と言えます。また、Lax-Wendroff法では界面前後の物理量が一致する(\({}^L\! q_{i+\frac{1}{2}}={}^R\! q_{i+\frac{1}{2}}\))のも特徴です。
以上より高次補正量\({}^R\! \delta q_{i+\frac{1}{2}},{}^L\! \delta q_{i+\frac{1}{2}}\)の勾配計算に、BeamWarming法は風上勾配、Fromm法は中心勾配、Lax-Wendroff法は風下勾配が利用されていることが分かりました。このため、BeamWarming法、Lax-Wendroff法の高次補正量の平均値をとるとFromm法と一致することが知られています。
界面物理量の連続性
ここまで求めたセル界面の物理量について、界面左右での連続性を確認してみます。例としてセル界面\(i+\frac{1}{2}\)の左右の物理量\({}^R\! q_{i+\frac{1}{2}},{}^L\! q_{i+\frac{1}{2}}\)の差分を考えます。
{}^R\! q_{i+\frac{1}{2}}-{}^L\! q_{i+\frac{1}{2}}=&\left[\bar{\cal{q}}_{i+1}
-\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i})-\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1})\right]\\
&-\left[\bar{\cal{q}}_{i}
+\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1})+\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i})\right]+O\left(\Delta x^3\right)\\
=&\frac{1}{2}(1-\kappa)(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i})
-\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1})-\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1})+O\left(\Delta x^3\right)\\
=&-\frac{1}{4}(1-\kappa)\left[-2(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i})
+(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1})+(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1})\right]+O\left(\Delta x^3\right)\\
=&-\frac{1}{4}(1-\kappa)\left(\bar{\cal{q}}_{i+2}-3\bar{\cal{q}}_{i+1}+3\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)+O\left(\Delta x^3\right)\tag{35}
\end{align}
ここで第1項の二番目の括弧内は4次精度中心差分の形をしているため以下のように変形できます。
{}^R\! q_{i+\frac{1}{2}}-{}^L\! q_{i+\frac{1}{2}}=&-\frac{1}{4}(1-\kappa)\left(\frac{\partial ^3 u}{\partial x^3}\Delta x^3 +O\left(\Delta x^4\right)\right)+O\left(\Delta x^3\right)\\
=&-\frac{1}{4}(1-\kappa)\left(\frac{\partial ^3 u}{\partial x^3}\Delta x^3 \right)+O\left(\Delta x^3\right)\tag{36}
\end{align}
上式より\(\kappa = 1\)ならば第一項が0になり完全な連続ではないものの、3次精度の誤差のみとなることが分かります。一方で\(\kappa \neq 1\)の場合、一項目(定数項)が残ってしまいます。つまり\(\kappa \neq 1\)の場合、界面を通り越した瞬間に物理量が不連続に変化してしまうことを意味しています。
界面を通り越しただけで物理量が変化するのは物理的におかしいので、本来ならば第一項は常に0となっていてほしいところです。しかし式\((5)\)の多項式近似にそのような制約が含まれていない以上、当たり前といえば当たり前の結果なのでしょう。
このように左右の界面物理量という観点で見ると条件によっては連続性が満たされないこともあります。連続性を満たさないということは保存則を満たさないということです。しかしながら、離散変数\(\bar{\cal{q}}_{i}\)(物理量のセル平均値)という観点で見るとBurgers方程式自体からくる要請で結局は保存則が常に満たされると考えられます。したがって界面物理量が不連続であっても致命的な問題にはならないのでしょう。
2セル線形補間の場合
ここまでは3セル2次補間により近似された補間関数について記述してきました。この補間関数は式\((16)\)にて一般化され、Fromm法、BeamWarming法、Lax-Wendroff法といった「3セル2次補間なのに空間2次精度」といった精度的には少々ややこしいスキーム達が導かれました。
これらの手法は2次精度なので最初から2セル線形補間を用いた場合も同様に導けるような気もします。そこで2セル線形補間を用いた場合、補間関数がどのような形になるのか実際に確認してみます。
\(Q_{i}(x)\)を空間2次精度まで考えるとすると式\((4)\)は\(M=1\)として以下のように書けます。
Q_i(x)&=c_{0}+c_{1}(x-x_{i})+O((x-x_{i})^{2})\tag{37}
\end{align}
式\((37)\)は未知数が2つ(\(c_{0},c_{1}\))なので、これらを決めるのには式\((29)\)以外に2つの式が必要です。したがって2種のステンシルを選ぶことになりますが、その選び方としては「風下差分(\(\bar{\cal{q}}_{i},\bar{\cal{q}}_{i+1}\))」、「中心差分(\(\bar{\cal{q}}_{i-1},\bar{\cal{q}}_{i+1}\))」、「風上差分(\(\bar{\cal{q}}_{i-1},\bar{\cal{q}}_{i}\))」の三種類があります。
ここでは例として中心差分(\(\bar{\cal{q}}_{i-1},\bar{\cal{q}}_{i+1}\))を用いることとします。すると補間関数の定義から以下の2つの制約条件が得られます。
&\bar{\cal{q}}_{i-1}=\frac{1}{\Delta x_{i-1}}\int_{i-\frac{3}{2}}^{i-\frac{1}{2}}Q_{i}(x)dx \tag{38}\\
&\bar{\cal{q}}_{i+1}=\frac{1}{\Delta x_{i+1}}\int_{i+\frac{1}{2}}^{i+\frac{3}{2}}Q_{i}(x)dx \tag{39}
\end{align}
式\((38),(39)\)を用いると\(c_{0},c_{1}\)は以下のように書けます。
&c_{0}=\frac{\bar{\cal{q}}_{i-1}+\bar{\cal{q}}_{i+1}}{2}\tag{40}\\
&c_{1}=\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i-1}}{2\Delta x}=\frac{\delta_{i}q}{\Delta x} \tag{41}
\end{align}
簡単のため、\(\Delta x = \Delta x_{i-1} = \Delta x_{i+1} \)として考えます。まず式\((38)\)に式\((37)\)を代入して、積分を実行します。
\bar{\cal{q}}_{i-1}=\frac{1}{\Delta x}\int_{i-\frac{2}{3}}^{i-\frac{1}{2}}c_{0}+c_{1}(x-x_{i})+O((x-x_{i})^{2})dx \tag{B1}
\end{align}
ここで\(A=x-x_{i}\)と置いて置換積分を行います。積分範囲は以下のように変化します。
| \(x\) | \(x_{i-\frac{2}{3}} \rightarrow x_{i-\frac{1}{2}}\) |
| \(A\) | \(x_{i-\frac{3}{2}} -x_{i}=-\frac{3\Delta x}{2}\rightarrow x_{i-\frac{1}{2}} -x_{i}=-\frac{\Delta x}{2}\) |
従って、式\((A1)\)は以下のように書けます。
\bar{\cal{q}}_{i-1}&=\frac{1}{\Delta x}\int_{-\frac{3\Delta x}{2}}^{-\frac{\Delta x}{2}}c_{0}+c_{1}A+O(A^{2})dx \\
&=\frac{1}{\Delta x}\left[c_{0}A+\frac{1}{2}c_{1}A^2+O(A^{3})\right]_{-\frac{3\Delta x}{2}}^{-\frac{\Delta x}{2}} \\
&=c_{0}-c_{1}\Delta x +O(\Delta x^{2})\tag{B2}
\end{align}
同様に式\((39)\)に式\((37)\)を代入して、積分を実行すると以下の式が得られます。
\bar{\cal{q}}_{i+1}&=c_{0}+c_{1}\Delta x+O(\Delta x^{2})\tag{B3}
\end{align}
以上、式\((B2),(B3)\)を用いて\(c_{0},c_{1}\)に関する連立方程式を解くと式\((40), (41)\)を得ることが出来ます。
これらを式\((37)\)に代入すると以下の式が得られます。
Q_i(x)&=\frac{\bar{\cal{q}}_{i-1}+\bar{\cal{q}}_{i+1}}{2}+\frac{\delta_{i}q}{\Delta x} (x-x_{i})+O((x-x_{i})^{2})\tag{42}
\end{align}
\(c_{0}\)は\(\bar{\cal{q}}_{i-1},\bar{\cal{q}}_{i+1}\)の平均値であるため、\(\bar{\cal{q}}_{i}\)の近似として考えると上式は式\((15)\)の第二項までに一致します。(この近似が実際に成り立つとは限りませんが、式\((15)\)と対応をとるためにそのように考えます。)
さらに界面物理量\({}^L\! q_{i+\frac{1}{2}}=Q_i(x_{i+\frac{1}{2}}),{}^R\! q_{i+\frac{1}{2}}=Q_{i+1}(x_{i+\frac{1}{2}})\)を計算します。
{}^L\! q_{i+\frac{1}{2}}&=Q_i(x_{i+\frac{1}{2}})=\frac{\bar{\cal{q}}_{i-1}+\bar{\cal{q}}_{i+1}}{2}+\frac{\delta_{i}q}{\Delta x} (x_{i+\frac{1}{2}}-x_{i})+O(\Delta x^{2})\\
&=\frac{\bar{\cal{q}}_{i-1}+\bar{\cal{q}}_{i+1}}{2}+\frac{\delta_{i}q}{2} +O(\Delta x^{2})\\
&=\frac{\bar{\cal{q}}_{i-1}+\bar{\cal{q}}_{i+1}}{2}+\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i-1}}{4} +O(\Delta x^{2})\\
&\sim \bar{\cal{q}}_{i+1}+\frac{1}{4}(\bar{\cal{q}}_{i-1}-\bar{\cal{q}}_{i+1})+O(\Delta x^{2})\tag{43}\\
{}^R\! q_{i+\frac{1}{2}}&=Q_{i+1}(x_{i+\frac{1}{2}})=\frac{\bar{\cal{q}}_{i}+\bar{\cal{q}}_{i+2}}{2}+\frac{\delta_{i+1}q}{\Delta x} (x_{i+\frac{1}{2}}-x_{i+1})+O(\Delta x^{2})\\
&=\frac{\bar{\cal{q}}_{i}+\bar{\cal{q}}_{i+2}}{2}-\frac{\delta_{i+1}q}{2} +O(\Delta x^{2})\\
&=\frac{\bar{\cal{q}}_{i-1}+\bar{\cal{q}}_{i+1}}{2}-\frac{\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i}}{4} +O(\Delta x^{2})\\
&\sim \bar{\cal{q}}_{i+1}-\frac{1}{4}(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i})+O(\Delta x^{2})\tag{44}\\
\end{align}
これらは前述したFromm法(表2)に一致しています。
以上のように、2セル線形補間の場合でも、3セル2次補間場合と同様の補間関数を導くことが出来ました。ただ少しややこしいのは、これはFromm法に限った話で、式\((29)\)において風上差分や風下差分を用いても、表2で示したBeamWarming法、Lax-Wendroff法と同様の定式化を得ることはできないようです。(これはFromm法の場合、前後対称なステンシルである中心差分法を採用しているためと考えられます。)
したがってFromm法、BeamWarming法、Lax-Wendroff法といった手法は、あくまで3セル2次補間を前提に定式化されている手法と考えておいたほうが良いのかもしれません。
\(\kappa\)による補間関数\(Q_{i}\)の変化
次に\(\kappa\)により補間関数\(Q_{i}\)がどのように変化するか確認します。以下はいくつかの\(\kappa\)で補間関数\(Q_{i}\)(式\((16)\))をプロットしたグラフです。セル平均値は仮に\(\bar{\cal{q}}_{i-1}=-2,\bar{\cal{q}}_{i}=0,\bar{\cal{q}}_{i+1}=1\)、セルサイズは\(\Delta x = 1\)としました。
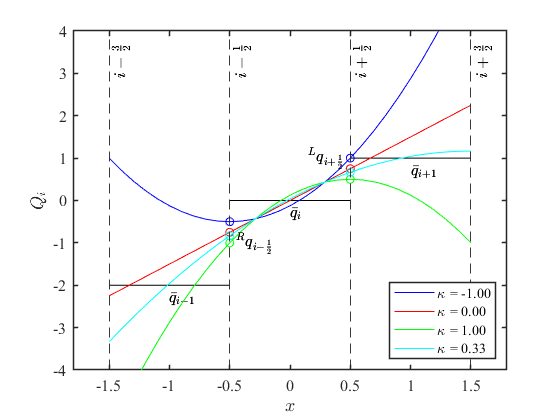
グラフより、いずれの補間関数も\(\bar{\cal{q}}_{i}\)に対し良好な一致を見せていることがわかります。
特に\(\kappa=\frac{1}{3}\)の場合は、セル平均値の直線と補間関数の曲線が成す面積の合計が0になっており、\(\bar{\cal{q}}_{i}\)だけでなく隣接セル\(\bar{\cal{q}}_{i-1},\bar{\cal{q}}_{i+1}\)においても比較的高い精度を保っています。これは\(\kappa=\frac{1}{3}\)では補間関数\(Q_{i}\)が式\((11)\sim(13)\)の制約条件を満たし3次精度になるためです。
一方、\(\kappa=\frac{1}{3}\)以外は隣接セル\(\bar{\cal{q}}_{i-1},\bar{\cal{q}}_{i+1}\)における誤差が比較的大きくなります。これは補間関数\(Q_{i}\)が式\((11)\sim(13)\)の制約条件を満さず、2次精度になるためと考えられます。
以上より補間関数の近似精度の面では3次精度である\(\kappa=\frac{1}{3}\)を用いるのがよさそうです。
MATLABコード
以下に空間高次精度を考慮し1次元線形移流方程式、および1次元非粘性Bugers方程式を求解するMATLABコードを示します。githubにもアップロードしました。
変数SW1を切り替えるとことで1次元線形移流方程式または1次元非粘性Bugers方程式のいずれかを選択できます。また変数SW2を切り替えることで不連続な初期値分布と連続な初期値分布のいずれかを選択できます。
% 初期化
clearvars;
% パラメーター
i_max = 100; % 格子セル数
XL = -1.0; % 計算領域左端の座標
XR = 1.0; % 計算領域右端の座標
a = 1.0; % 線形移流方程式の移流速度
tstop = 1; % 計算停止時刻
eps = 1; % 高次精度解法のパラメーター
kappa = 0; % 高次精度解法のパラメーター
% 配列定義
i = 0; % セル番号; (i番目セルの左境界の番号はi、右辺境界の番号はi+1とする)
x = zeros(i_max + 1, 1); % セル境界の座標
u = zeros(i_max, 1); % セル平均値 (数値解)
ue = zeros(i_max, 1); % セル平均値 (厳密解)
ul = zeros(i_max + 1, 1); % セル境界左側の変数値
ur = zeros(i_max + 1, 1); % セル境界右側の変数値
f = zeros(i_max + 1, 1); % セル境界の流束
n = 0; % 時間ステップ
t = 0; % 計算時間
% 方程式を選択
% 1:線形移流方程式、2:非粘性Burgers方程式
sw1 = 1;
% 初期値の選択
% 1:不連続な分布、2:滑らかな分布
sw2 = 1;
% メッシュの設定
dx = (XR - XL) / (i_max - 4.0); % 格子間隔 計算領域外に二つずつ余分なセルを準備。周期的境界条件向けの設定
dt = 0.2 * dx; % 時間刻み
x(1) = XL - 2.0 * dx; % 計算領域外の2セルも考慮した座標を振る。
[x, u] = initc(sw2, i_max, x, dx, u); % 計算格子,時間刻み,初期条件を設定する
% 厳密解の計算
ue = exact(sw1, sw2, i_max, ue, x, t, dx);
% メインループ
while t <= tstop
% 時間発展
n = n + 1;
t = t + dt;
% 空間再構築
[ul, ur] = reconstruction_pc(i_max, u, ul, ur, eps, kappa);
% リーマンソルバー
f = riemann_roe(i_max, f, ul, ur, sw1);
% 時間積分
u = update(i_max, u, dt, dx, f);
% 境界条件
u = bc(i_max, u);
% 厳密解を求める
ue = exact(sw1, sw2, i_max, ue, x, t, dx);
% 時間表示
fprintf("n=%d, t=%f \n", n, t);
% 動画保存
if n == 1
plotconfig(x(1 : end - 1), ue, u, t, eps, kappa)
filename = ['sw1 = ', num2str(sw1, '%.0f'), ', sw2 = ', num2str(sw2, '%.0f'), ', epsilon = ', num2str(eps, '%.0f'), ', kappa = ', num2str(kappa, '%.3f'),'.mp4'];
v = VideoWriter(filename,'MPEG-4');
v.FrameRate = 40;
open(v);
else
plotconfig(x(1 : end - 1), ue, u, t, eps, kappa)
frame = getframe(gcf);
writeVideo(v,frame);
end
end
% 動画ファイルを閉じる
close(v);
%% 以下ローカル関数
% 初期値の設定
function [x, u] = initc(sw2, i_max, x, dx, u)
for i = 2 : i_max + 1
x(i) = x(i - 1) + dx;% 格子点の座標
end
switch sw2
case 1 % 初期の変数値(滑らかな分布)
for i = 1 : i_max
u(i) = 0.1;
end
for i = i_max / 2 - 10 : i_max / 2 + 10
u(i) = 1.0;
end
case 2 % 初期の変数値(不連続な分布)
for i = 1 : i_max
u(i) = 0.5*(1.1 + sin(2.* pi *(x(i)-x(3))));% 三番目の要素(XL、XRの座標値)を基準に考える。
end
end
end
% 厳密解の計算(不連続分布)
function [ue] = exact(sw1, sw2, i_max, ue, x, t, dx)
switch sw2
case 1 % 不連続分布
switch sw1
case 1 % 線形移流方程式
alpha_12 = 1;% 移流速度
xc = alpha_12 * t;
xl = xc - dx * 10;% 中央に対して10要素だけマイナスに移動した位置
% 周期境界条件
if xl > 1.0
xl = -2.0 + xl;
end
xr = xc + dx * 10.;
% 周期境界条件
if xr > 1.0
xr = -2.0 + xr;
end
if xl <= xr
for i = 1 : i_max
ue(i) = 0.1;
if dx * (i - i_max / 2) >= xl && dx * (i - i_max / 2) <= xr
ue(i) = 1.0;
end
end
end
if xl >= xr
for i = 1 : i_max
ue(i) = 1.0;
if dx * (i - i_max / 2) >= xr && dx * (i - i_max / 2) <= xl
ue(i) = 0.1;
end
end
end
case 2 % 非粘性burgers方程式
xc = - dx * 10 + t;
xl = - dx * 10 + 0.1 * t;
xr = dx * 10 + 0.55 * t;
% 周期境界条件
if xl > 1.0
xl = -2.0 + xl;
end
% 周期境界条件
if xr > 1.0
xr = -2.0 + xr;
end
% 周期境界条件
if xc > 1.0
xc = -2.0 + xc;
end
for i = 1 : i_max
if x(i) <= xl
ue(i) = 0.1;
end
if x(i) >= xl && x(i) <= xc
ue(i) =(x(i) - xl) / (xc - xl) * 0.9 + 0.1;
end
if x(i) >= xc && x(i) <= xr
ue(i) = 1.0;
end
if x(i) >= xr
ue(i) = 0.1;
end
end
end
case 2 % 連続分布
switch sw1
case 1 % 線形移流方程式
alpha_12 = 1; % 移流速度
for i = 1 : i_max
ue(i) = 0.5 * (1.1 + sin(2. * pi * ((x(i) - x(3)) - alpha_12 * t)));
end
case 2 % 非粘性burgers方程式
for i = 1 : i_max
c = 2 * pi;
f = ue(i) - 0.5 * (1.1 + sin(c * (x(i)-x(3) - ue(i) * t)));
df = 1.0 + 0.5 * c * cos(c *(x(i) - x(3) - ue(i) * t)) * t;
count = 0;
while abs(f) >= 1.0e-6
count = count + 1;
ue(i) = ue(i) - f / df; % ニュートン法の計算式*/
f = ue(i) - 0.5 * (1.1 + sin(c*((x(i) - x(3) - ue(i) * t))));
df = 1.0 + 0.5 * c * cos(c * ((x(i) - x(3) - ue(i) * t))) * t;
if count > 10000
disp("厳密解が収束しないので反復を打ち切ります。");
break
end
end
end
end
end
end
% 厳密解の計算(初期値が滑らかな分布の場合)
function [ue] = exact2(sw1, i_max, ue, x, t, dx)
switch sw1
case 1 % 線形移流方程式
alpha_12 = 1; % 移流速度
for i = 1 : i_max
ue(i) = 0.5 * (1.1 + sin(2. * pi * ((x(i) - x(3)) - alpha_12 * t)));
end
case 2 % 非粘性burgers方程式
for i = 1 : i_max
c = 2 * pi;
f = ue(i) - 0.5 * (1.1 + sin(c * (x(i)-x(3) - ue(i) * t)));
df = 1.0 + 0.5 * c * cos(c *(x(i) - x(3) - ue(i) * t)) * t;
count = 0;
while abs(f) >= 1.0e-6
count = count + 1;
ue(i) = ue(i) - f / df; % ニュートン法の計算式*/
f = ue(i) - 0.5 * (1.1 + sin(c*((x(i) - x(3) - ue(i) * t))));
df = 1.0 + 0.5 * c * cos(c * ((x(i) - x(3) - ue(i) * t))) * t;
if count > 10000
disp("厳密解が収束しないので反復を打ち切ります。");
break
end
end
end
end
end
function [ul, ur] = reconstruction_pc(i_max, u, ul, ur, eps, kappa)
for i = 2 : i_max - 2
ul(i + 1) = u(i) + eps * (0.25 * (1 - kappa) * (u(i) - u(i - 1))...
+ 0.25 * (1 + kappa) * (u(i + 1) - u(i))); % セル境界(i+1/2)左側の値
ur(i + 1) = u(i + 1) + eps *(- 0.25 * (1 + kappa) * (u(i + 1) - u(i))...
- 0.25 * (1 - kappa) * (u(i + 2) - u(i + 1))); % セル境界(i+1/2)右側の値
end
end
function [f] = riemann_roe(i_max, f, ul, ur, sw1) % 流束を計算する
% 移流速度の計算
switch sw1
case 1 % 線形移流方程式の数値流束
for i = 3 : i_max - 1
alpha_12 = 1;% 移流速度
f_flux_ul = alpha_12 * ul(i);
f_flux_ur = alpha_12 * ur(i);
f(i) = 1.0 / 2.0 * (f_flux_ul + f_flux_ur) - 1.0 / 2.0 * abs(alpha_12) * (ur(i) - ul(i));
end
case 2 % 非粘性burgers方程式の数値流束
for i = 3 : i_max - 1
alpha_12 = 0.5 * (ur(i) + ul(i));% 移流速度
f_flux_ul = 0.5 * ul(i) * ul(i);
f_flux_ur = 0.5 * ur(i) * ur(i);
f(i) = 1.0 / 2.0 * (f_flux_ul + f_flux_ur) - 1.0 / 2.0 * abs(alpha_12) * (ur(i) - ul(i));
end
end
end
function [u] = update(i_max, u, dt, dx, f)
for i = 3 : i_max - 2
u(i) = u(i) - dt / dx * (f(i + 1) - f(i));% 計算変数を更新する
end
end
function [u] = bc(i_max, u) % 周期境界条件
u(1) = u(i_max - 3); % 計算領域左端の境界条件
u(2) = u(i_max - 2); % 計算領域左端の境界条件
u(i_max - 1) = u(3); % 計算領域右端の境界条件
u(i_max) = u(4); % 計算領域右端の境界条件
end
function [] = plotconfig(x, ue, u, t, eps, kappa)
plot(x, ue, x, u)
%plot(x, u)
title(['time = ', num2str(t, '%.3f')]);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 12);
axis equal;
axis tight;
axis on;
fig=gcf;
fig.Color='white';
ylim([-0.2 1.5]);
xlabel('x')
ylabel('u')
% 凡例
method = ['\epsilon = ', num2str(eps, '%.0f'), ', \kappa = ', num2str(kappa, '%.3f')];
legend({'exact', method},'Location','southwest','FontSize', 10)
% 新しいプロットの時、軸設定を保持したまま前のグラフィックスオブジェクトを消去
set(gca,'nextplot','replacechildren');
end
実行結果
以下に実行結果を示します。今回はより動きが分かりやすい、線形移流方程式の結果を示します。
まず\(\epsilon=0,\kappa=0\)の結果です。この場合、1次精度風上法になります。数値粘性の影響で解が鈍っていく様子が確認できます。
次に\(\epsilon=1,\kappa=1\)の結果です。この場合、空間2次精度のLax-Wendroff法になります。波形が振動して発散していく様子が確認できます。ゴルドフの定理より高次精度は数値振動から逃れられません。
最後に\(\epsilon=1,\kappa=\frac{1}{3}\)の結果です。この場合、空間3次精度になります。高次精度である以上、ゴルドフの定理からは逃れられませんが、2次精度よりも発散の仕方がやや緩やかなようです。
おわりに
今回は1次元非粘性Bugers方程式および線形移流方程式について空間高次精度を考慮した有限体積法による解法をまとめました。計算結果的には差分法と同等ですが、有限体積法における高次精度のアプローチは差分法よりだいぶ複雑になることが分かりました。
例えば今回は簡単のため等間隔格子を想定し、\(\Delta x = \Delta x_{i-1}= \Delta x_{i} = \Delta x_{i+1} \)として各種式を求めましたが、これが非等間隔格子になるだけで大分複雑な定式化になるように思います。また式\((16)\)の一般化式はMUSCL法の説明でよく出てきますが、精度と補間関数の次数の関係がやや複雑なため、自分なりにかみ砕くのに苦労しました。
ともあれ考え方のエッセンスは学べたので空間高次精度はいったんここまでにして、次は時間高次精度についてまとめていきたいと思います。
参考文献
[1] 肖 鋒, “数値流体解析の基礎- Visual C++とgnuplotによる圧縮性・非圧縮性流体解析 -“, コロナ社, 2020



コメント