はじめに
前回記事では二元系合金の異相平衡状態において、自由エネルギー曲線の共通接線を見出すことで、どのような相状態が実現するか導けることを示しました。この際、自由エネルギー曲線は下に凸な関数と仮定しグラフ化しましたが、具体的な数式の形は示していませんでした。そこで今回は固溶体におけるギブスの自由エネルギーの定式化についてまとめたいと思います。
2元系合金の自由エネルギー定式化
ギブスの自由エネルギーはもともとは「系から取り出せる非膨張仕事の最大量」を示すのでした。したがって相が異なると原子の配置や結合の強さが異なるため、異なるギブズの自由エネルギーを持つことになります。
ここで天下り的ではありますが、今後導出する固相(置換型固溶体)および液相を持つ2元系合金のギブスの自由エネルギーを以下に示します。

これらはいわゆる正則溶体近似による定式化として知られ、状態図を説明する最も基本的なモデルです。最も基本的とはいえ、上式にたどり着くにはいくつかの段階を経る必要があります。今回の記事ではこれらのうち、まずは固相(置換型固溶体)のギブスの自由エネルギーの導出を行います。
固溶体のギブスの自由エネルギー
ここからは置換型固溶体のギブスの自由エネルギーを導出していきます。こちらも最初に求める式を以下に示します。
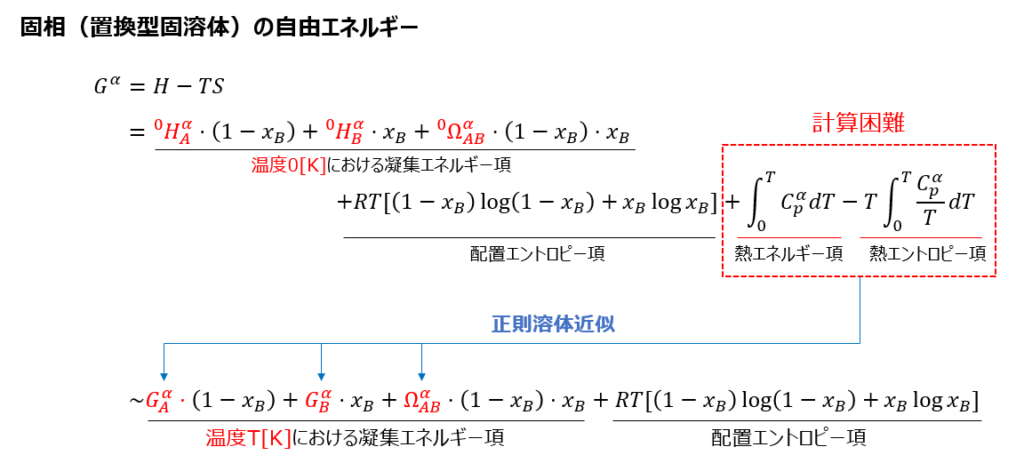
固溶体のギブスのエネルギーは凝集エネルギー項、配置エントロピー項、熱エネルギー項、熱エントロピー項からなり、それらに正則溶体近似を施すことで最終的な形が得られます。各項について順に求めていきましょう。
一般にギブスの自由エネルギー\(G\)はエンタルピー\(H\)、エントロピー\(S\)、温度\(T\)を用いて、以下のように与えられました。
G=H-TS\tag{1}
\end{align}
エンタルピーは定圧過程では熱量そのものを表すので以下のように書けます。(実際の実験系においては大気圧で一定であることを想定して計算しています。また圧力依存性を考慮しても一般的な金属の場合、その影響は小さいことが知られています。)
& dH=dQ=C_{p}dT\\
& \rightarrow
H=^{0}\!\!\!H+\int_{0}^{T}C_{p}dT \tag{2}
\end{align}
ここで第一項は\(^{0}\!H\)は絶対零度\(T=0[\rm{K}]\)における凝集エネルギー、第二項\(\int_{0}^{T}C_{p}dT\)は熱エネルギー、\(C_{p}\)は固溶体の定圧比熱です。(※凝集エネルギー:結晶または物質を構成する原子や分子が無限に離れた状態から集まって固体を形成する際に必要とされるされるエネルギー)
例えば、純チタンの場合、\(0[\rm{K}]\)における凝集エネルギーは\(^{0}\!H \sim-46000[\rm{J/mol}]\)程度、また熱エネルギーは\(1000\rm{[K]}\)において\(\int_{0}^{T}C_{p}dT\sim25000[\rm{J/mol}]\)程度となります。
同様にエントロピーは定圧過程を仮定すると以下のように書けます。
& dS=\frac{dQ}{T}=\frac{C_{p}dT}{T}\\
& \rightarrow
S=^{0}\!\!\!S+\int_{0}^{T}\frac{C_{p}}{T}dT\tag{3}
\end{align}
ここで第一項\(^{0}\!S\)は絶対零度\(T=0[\rm{K}]\)におけるエントロピーであり、純粋な金属や化合物の場合には熱力学第三法則により0になります。しかし溶液や固溶体のような2種以上の原子が混ざり合っている物質では、後述の通り、配置エントロピーの寄与により0になりません。
また第二項\(\int_{0}^{T}\frac{C_{p}}{T}dT\)は熱エントロピー(または振動エントロピー)と呼ばれ、例えば純チタン\(1000\rm{[K]}\)における値はおよそ\(60[\rm{J/mol}]\)程度とされています。
以上より式\((2),(3)\)を式\((1)\)に代入すると以下の式が得られます。
& G=H-TS\\\
& \rightarrow
G=^{0}\!\!\!H-T^{0}\!S+\int_{0}^{T}C_{p}dT -T\int_{0}^{T}\frac{C_{p}}{T}dT\tag{4}
\end{align}
ここまでが前準備です。次節からさらに各項を求めていきます。
凝集エネルギー\(^{0}\!H\)
まず式\((4)\)における凝集エネルギー\(^{0}\!H\)について求めていきます。置換型固溶体のエンタルピーは以下のブラッグ-ウィリアムズの仮定(または最近接仮定)の下、近似として表現されます。
- ランダム分布の仮定
結晶格子内の各位置に原子が占める確率は、結晶全体の平均組成によって決まるものとする。例えば、ある固溶体が原子Aと原子Bの混合物で、原子Aの割合が50%であれば、結晶格子の任意の位置に原子Aが存在する確率も50%とされる。このため、特定の原子の周りに特定のパターン(例えば原子Aの周りには常に原子Bが多く存在するなど)があるような局所的な組成の変動は考慮できない。 - 短距離相互作用の仮定
固溶体の凝集エネルギーは最近接原子間の結合エネルギーの総和とみなし、第2隣接位置以上離れた原子間の結合エネルギーは無視するものとする。このため、より複雑な相互作用や長距離秩序を持つシステムの表現できない。
まず簡単のために、金属Aも金属Bも同一の結晶構造を持ち、全率可溶である場合について考えます。固溶体を構成している原子Aの数を\(N_{A}\)、原子Bの数を\(N_{B}\)、原子A・原子Bの総和を\(N\)とします。また、各原子のモル分率を\(x_{A},x_{B}\)とすると以下の式が成り立ちます。
& N_{A}=N \cdot x_{A}=N\cdot(1-x_{B})\\
& N_{B}=N \cdot x_{B}\\
\tag{5}
\end{align}
ここで、1つの原子を取り囲む最近接原子の数を\(z\)とすると上記ランダム分布の仮定より、\(z\)個のうち平均して\(zx_{A}\)個が原子Aであると考えられます。この為、A-A対の総数\([AA]\)は\(N_{A} z x_{A}\cdot\frac{1}{2}\)となります。\(\frac{1}{2}\)はダブルカウントを防ぐ係数です。
同様にB-B対の総数\([BB]\)、A-B対の総数\([AB]\)もまとめると以下のようになります。
& [AA]=N_{A} z x_{A}\cdot\frac{1}{2}=\frac{1}{2}\left(x_{A}N\right) zx_{A}=\frac{1}{2}N z\left(1- x_{B}\right)^2 \\
& [BB]=N_{B} z x_{B}\cdot\frac{1}{2}=\frac{1}{2}\left(x_{B}N\right) zx_{B}=\frac{1}{2}N zx_{B}^2 \\
& [AB]=N_{B} z x_{A}=N_{A} z x_{B}=\left(x_{A}N\right) z x_{B}=N z x_{B}(1-x_{B})\\
\tag{6}
\end{align}
以下に最近接原子数\(z=2\)を例に結晶モデルと原子対の総数の計算結果を示します。
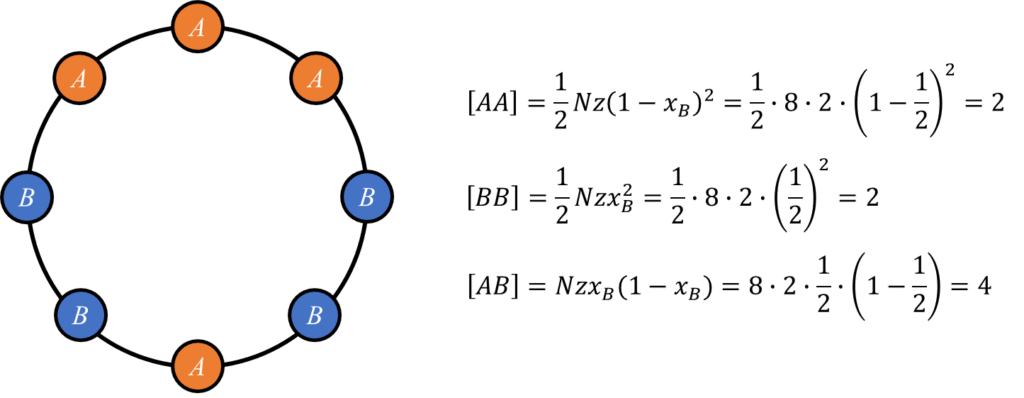
さらにA-A対、B-B対、A-B対の一対当たりの\(0\rm{[K]}\)における結合エネルギーを\(e_{AA},e_{BB}\)および\(e_{AB}\)とすると、\(\alpha\)固溶体の\(0\rm{[K]}\)におけるエンタルピー\(^{0}\!H^{\alpha}\)は以下のように書けます。
^{0}\!H^{\alpha}&=[AA]\cdot e_{AA} +[BB]\cdot e_{BB} +[AB]\cdot e_{AB} \\
&=\frac{N z}{2}\left[ e_{AA} \left(1- x_{B}\right)^2+e_{BB} x_{B}^2+2e_{AB} (1-x_{B})x_{B}\right] \\
&=\frac{N z}{2}\left[ e_{AA} \left(1- x_{B}\right)\left(1- x_{B}\right)+e_{BB} x_{B}\left(1-1+x_{B}\right)+2e_{AB} (1-x_{B})x_{B}\right] \\
&=\frac{N z}{2}\left[ e_{AA} \left(1- x_{B}\right)- e_{AA} \left(1-x_{B}\right)x_{B}+e_{BB} x_{B}-e_{BB} x_{B}\left(1-x_{B}\right)+2e_{AB} (1-x_{B})x_{B}\right] \\
&=\frac{N z}{2}\left[ e_{AA} \left(1- x_{B}\right)+e_{BB} x_{B}- e_{AA} \left(1-x_{B}\right)x_{B}-e_{BB} x_{B}\left(1-x_{B}\right)+2e_{AB} (1-x_{B})x_{B}\right] \\
&=\frac{N z}{2}\left[ e_{AA} \left(1- x_{B}\right)+e_{BB} x_{B}+2\left(e_{AB}-\frac{e_{AA}+e_{BB}}{2} \right) (1-x_{B})x_{B} \right] \\
&=^{0}\!\!\!H_{A}^\alpha \left(1- x_{B}\right)+^{0}\!\!\!H_{B}^\alpha x_{B}+^{0}\!\!\Omega_{AB}^{\alpha} (1-x_{B})x_{B}
\tag{7}
\end{align}
ここで\(^{0}\!H_{A}^\alpha =\frac{Nze_{AA}}{2}\)、\(^{0}\!H_{B}^\alpha =\frac{Nze_{BB}}{2}\)、\(^{0}\Omega_{AB}^{\alpha} =2\left(e_{AB}-\frac{e_{AA}+e_{BB}}{2} \right)\)としています。
「金属A、Bからなる固溶体のエンタルピー」=「純金属Aのエンタルピー」+「純金属Bのエンタルピー」+「金属ABの結合によるエンタルピー」が成り立つとすると、\(^{0}\!H_{A}^\alpha \)は純金属Aの\(0\rm{[K]}\)における1モル当たりのエンタルピー、\(^{0}\!H_{B}^\alpha \)は純金属Bの\(0\rm{[K]}\)における1モル当たりのエンタルピー、\(^{0}\Omega_{AB}^{\alpha} \)は金属ABの\(0\rm{[K]}\)における結合によるエンタルピーと解釈してよいでしょう。
\(^{0}\!H_{A}^\alpha, ^{0}\!H_{B}^\alpha \) は純金属AおよびBの値なので、過去の実験データから既知の値として与えることが出来ます。しかし\(^{0}\Omega_{AB}^{\alpha} \)に関してはA-B2元系の\(\alpha\)固溶体に特有の値なので、実験的に調査する必要があります。通常、この値は\(\alpha\)固溶体におけるAまたはB成分の活量の測定値に基づいて定めることが出来ます。(活量は実際の溶液が理想溶液の挙動からどの程度逸脱しているかを示す量です。測定方法もいくつかあるらしいので、今後調べてみたい。)
最後に\(^{0}\Omega_{AB}^{\alpha} \)の物理的な意味について考えます。
- \(^{0}\Omega_{AB}^{\alpha} >0\)すなわち\(e_{AB} >\frac{(e_{AA} +e_{BB}) }{2}\)のとき
ギブスの自由エネルギー最小化の観点から考えると、式\((1)\)より、エンタルピーは小さいほうが望ましいことが分かります。A-B対のエネルギーがA-A対およびB-B対の平均エネルギーよりも高く不安定であるから、原子Aと原子Bは\(\alpha\)固溶体の中で反発的であり、原子A同士と原子B同士が寄り集まってクラスタリングが起こり、さらにはAを主体とする相とBを主体とする相の二つに分離する傾向にあります。 - \(^{0}\Omega_{AB}^{\alpha} <0\)すなわち\(e_{AB} <\frac{(e_{AA} +e_{BB}) }{2}\)のとき
A-B対がA-A対およびB-B対よりも安定であるから、\(\alpha\)固溶体の中で引きあうような傾向があり、極端な場合には固溶体を構成する原子Aと原子BがすべてA-B-A-Bと交互に並びます。これを規則化と呼びます。 - \(^{0}\Omega_{AB}^{\alpha} =0\)すなわち\(e_{AB} =\frac{(e_{AA} +e_{BB}) }{2}\)のとき
A-B対のエネルギーがA-A対およびB-B対の平均値であるから、原子Aと原子Bの間には特別な相互作用が存在せず、原子A,Bの配置は無秩序であると考えられます。この種の固溶体は理想溶体と呼ばれます。
以上で凝集エネルギー\(^{0}\!H\)を導くことが出来ました。
配置エントロピー\(^{0}\!S\)
次に式\((4)\)における配置エントロピー\(^{0}\!S\)について求めていきます。一般に原子の集合体のエントロピー\(S\)は、原子配置の組み合わせの数(状態数)\(W\)を用いて以下のように定義されました。
S=k\cdot \log W\tag{8}
\end{align}
ここで\(k\)はボルツマン定数で\(k=0.86\times10^{-4}\rm{[eV/K]}\)です。上式の定義により、純金属のような単一元素からなる金属では、その配置方法は1通りなので、エントロピーは\(0\rm{[K]}\)において\(0\)になることが分かります。これは熱力学の第3法則と同等の結果です。(\(0\rm{[K]}\)より大きい場合、原子は熱による振動をしており、異なるエネルギー準位を有するため、状態数\(W\)は0になりません。)
では2種の原子を混合した2元系合金の場合はどうでしょうか?\(N_{A}\)個の原子Aと\(N_{B}\)個の原子Bを混ぜ合わせて、\(\alpha\)固溶体の格子点に無秩序に配置する組み合わせ数は以下の通りに書けます。
W_{AB}^{\alpha}=\frac{(N_{A}+N_{B})!}{N_{A}! \cdot N_{B}!}\tag{9}
\end{align}
例えば、\(N_{A}=N_{B}=8\)個の場合の配置の組み合わせ数は以下の図の通り、\({}_{16}C_8=12870\)通りあります。
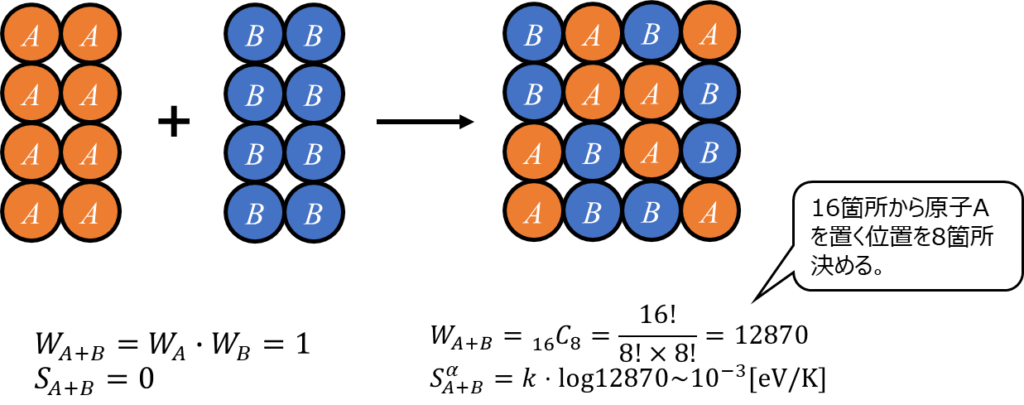
すなわち、2元系合金の場合、\(0\rm{[K]}\)であっても配置によるエントロピーが発生し、エントロピーは\(0\)になりません。
2元系合金の固溶体の状態における1mol当たりのエントロピーは、\(N_{A}+N_{B}=N=6.025 \times 10^{23}\)(アボガドロ数)が非常に大きな数値であることを考慮して次のスターリンの近似式が適用できます。
\log {N!}=N\log {N}-N\tag{10}
\end{align}
式\((8)\)に式\((9)\)を代入し、スターリンの近似式\((10)\)を用いると以下のように書けます。
^{0}\!S_{AB}^\alpha&=k\log {W_{AB}^{\alpha}}=k\log {\frac{(N_{A}+N_{B})!}{N_{A}! \cdot N_{B}!}}\\
&\sim
k\left[\log {(N_{A}+N_{B})!}-\log{N_{A}!}-\log{N_{B}!}\right]\\
&=
k\left[(N_{A}+N_{B})\log {(N_{A}+N_{B})}-(N_{A}+N_{B})-\left(N_{A}\log{N_{A}}-N_{A}\right)-\left(N_{B}\log{N_{B}}-N_{B}\right)\right]\\
&=
k\left[(N_{A}+N_{B})\log {(N_{A}+N_{B})}-N_{A}\log{N_{A}}-N_{B}\log{N_{B}}\right]\\
&=
k\left[N_{A}\log {(N_{A}+N_{B})}+N_{B}\log {(N_{A}+N_{B})}-N_{A}\log{N_{A}}-N_{B}\log{N_{B}}\right]\\
&=
k\left[-N_{A}\left(\log{N_{A}}-\log {(N_{A}+N_{B})}\right)-N_{B}\left(\log{N_{B}}-\log {(N_{A}+N_{B})}\right)\right]\\
&=
-k(N_{A}+N_{B})\left[\frac{N_{A}}{N_{A}+N_{B}}\left(\log{\frac{N_{A}}{N_{A}+N_{B}}}\right)+\frac{N_{B}}{N_{A}+N_{B}}\left(\log{\frac{N_{B}}{N_{A}+N_{B}}}\right)\right]\\
&=
-kN\left(x_{A}\log{x_{A}}+x_{B}\log{x_{B}}\right)\\
&=
-R\left[(1-x_{B})\log{(1-x_{B})}+x_{B}\log{x_{B}}\right]\tag{11}
\end{align}
ここで、\(R=kN=8.314\rm{[J/・Kmol]}\)は気体定数です。上式についてグラフ化すると以下のようになります。対数関数は0から1の間で負を取るため、\(^{0}\!S_{AB}^\alpha\)は常に正の値をとなることに注意しましょう。
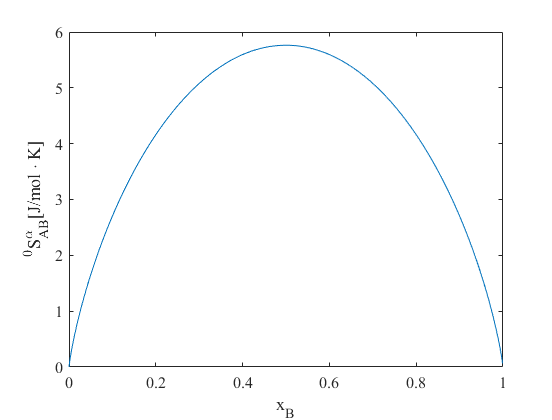
以上のように\(^{0}\!S_{AB}^\alpha\)は原子A、Bを結晶の格子点上に配置するために生じるエントロピーなので、配置エントロピーと呼ばれます。あるいは原子A、Bを混合したために生じたエントロピーとも考えられるので、混合エントロピーとも呼ばれます。
グラフより配置エントロピーは\(x_{B}=0.5\)でピークを取ることが分かります。ギブスの自由エネルギー最小化の観点でいうと、式\((1)\)よりエントロピーは最大化したいので、配置エントロピーのみ考えれば2元系合金は原子Aと原子Bが半々で存在するときが、最も安定と言えます。
これは原子Aと原子Bが半々で存在する際は原子の取り得る状態数が最も高く、システムが変化(温度変化など)に対してより柔軟になるためと考えられます。互いの原子が動くためのスペースが多くあるためと考えてもよいでしょう。逆に純金属の場合は状態数が1となるため、あらゆる変化に対してその一つの状態しかとりえないので、不安定な状態といえます。例えば鉄は空気中で放っておくだけで、錆が発生してしまうのもこのためです。
正則溶体近似
ここまでに、以下の凝集エネルギー\(^{0}\!H\)(式\((7)\))と配置エントロピー\(^{0}\!S\)(式\((11)\))を求めました。
^{0}\!H^{\alpha}&=^{0}\!\!\!H_{A}^\alpha \left(1- x_{B}\right)+^{0}\!\!\!H_{B}^\alpha x_{B}+^{0}\!\!\Omega_{AB}^{\alpha} (1-x_{B})x_{B}
\tag{7}\\
^{0}\!S_{AB}^\alpha&=-R\left[(1-x_{B})\log{(1-x_{B})}+x_{B}\log{x_{B}}\right]\tag{11}
\end{align}
これらを式\((4)\)に代入すると、A-B2元系\(\alpha\)固溶体のギブスの自由エネルギー\(G^{\alpha}\)は以下のように書けます。
G^{\alpha}=&^{0}\!H^{\alpha}-T^{0}\!S_{AB}^\alpha+\int_{0}^{T}C_{p}dT -T\int_{0}^{T}\frac{C_{p}}{T}dT\\
=&^{0}\!H_{A}^\alpha \left(1- x_{B}\right)+^{0}\!\!\!H_{B}^\alpha x_{B}+^{0}\!\!\Omega_{AB}^{\alpha} (1-x_{B})x_{B} \\
&+RT\left[(1-x_{B})\log{(1-x_{B})}+x_{B}\log{x_{B}}\right]+\int_{0}^{T}C_{p}dT -T\int_{0}^{T}\frac{C_{p}}{T}dT\tag{12}
\end{align}
ここで注意したいのは、上式を求めた際の考え方が「\(0\rm{[K]}\)における金属Aと金属Bのエンタルピー\(^{0}\!H^{\alpha}\)」と「これらを混合したために生ずる配置エントロピー\(^{0}\!S_{AB}^\alpha\)」の和を出発点として、これに\(0\rm{[K]}\)から\(T\rm{[K]}\)までの「熱エネルギー項\(\int_{0}^{T}C_{p}dT\)」と「熱エントロピー項\(T\int_{0}^{T}\frac{C_{p}}{T}dT\)」を加算するという手順を踏んでいる点です。
この為、結合によるエンタルピー\(^{0}\!\Omega_{AB}^{\alpha} \)の値を定めるとともに、固溶体の定圧比熱\(C_{p}\)の値を正確に知る必要があります。しかし、固溶体の比熱を正確に理論計算することは困難なので、実際には各組成の固溶体の比熱を測定しなくてはいけないことになります。
この様な煩雑さを避ける意味で\(T\rm{[K]}\)における金属Aと金属Bの自由エネルギー値を出発点にすれば、\(\alpha\)固溶体の\(T\rm{[K]}\)における自由エネルギーが次のように簡略に表現され、\(^{0}\!\Omega_{AB}^{\alpha} \)の値のみを定めれば計算できるようになります。
G^{\alpha}=G_{A}^\alpha \left(1- x_{B}\right)+G_{B}^\alpha x_{B}+\Omega_{AB}^{\alpha} (1-x_{B})x_{B} +RT\left[(1-x_{B})\log{(1-x_{B})}+x_{B}\log{x_{B}}\right]\tag{13}
\end{align}
ここで\(G_{A}^\alpha,G_{B}^\alpha \)は\(T\rm{[K]}\)における純金属A、Bのギブスの自由エネルギー、\(\Omega_{AB}^{\alpha} \)は\(T\rm{[K]}\)における純金属A、Bの結合によるギブスの自由エネルギーを示しています。
これらの係数は一般に温度に依存します。しかし実際の温度依存性を調べることは困難です。この為、計算上は固相の純金属のギブスの自由エネルギーを基準して、\(G_{A}^\alpha,G_{B}^\alpha \)の項は消去してしまうことが多いです。また\(\Omega_{AB}^{\alpha} \)は簡単のため温度に依存しない定数として利用するのが一般的です。
上記のような近似を正則溶体近似と呼び、溶液や合金の熱力学的解析にしばしば用いられます。
要は本来ならば固溶体の定圧比熱の積分で得るべきエンタルピーとエントロピーを「ある温度のギブスの自由エネルギーは、その温度における【純金属のギブスの自由エネルギー】と【原子A,Bの結合によるギブスの自由エネルギー】の和として表現される。」という仮定に基づいて、ある意味強引に係数に割り振ってしまうわけです。

当然ですが、式\((12)\)と式\((13)\)は厳密に一致するものではありません。個人的には熱エントロピー項まで凝縮エネルギー項(もともとはエンタルピーから発生する項)に割り振ってしまう点や、その一方で配置エントロピーだけそのまま残しておく点に当初違和感を覚えましたが、ギブスの自由エネルギーとモル分率\(x_{B}\)の関係性を知れればいいという意味では問題ない近似なのでしょう。
グラフ化
最後に式\((13)\)に基づき、正則溶体近似による固溶体の自由エネルギーとモル分率\(x_{B}\)の関係をグラフ化します。原子間の結合によるエントロピーは\(^{0}\!\Omega_{AB}^{\alpha}=12000,0,-12000 \rm{[J/mol]}\)、温度は\(T=0,500,1000\rm{[K]}\)のそれぞれ三水準を考えるものとします。
また、前述の通り、\(T\rm{[K]}\)における純金属A、Bのギブスの自由エネルギー\(G_{A}^\alpha (1-x_{B})+G_{B}^\alpha x_{B}\)を基準点とすることとして、以下の\(\Delta G^{\alpha}\)についてプロットすることとします。
\Delta G^{\alpha}&=G^{\alpha}-\left[G_{A}^\alpha \left(1- x_{B}\right)+G_{B}^\alpha x_{B}\right]\\
&=\Omega_{AB}^{\alpha} (1-x_{B})x_{B} +RT\left[(1-x_{B})\log{(1-x_{B})}+x_{B}\log{x_{B}}\right]\tag{13}
\end{align}
以下に結果のグラフを示します。
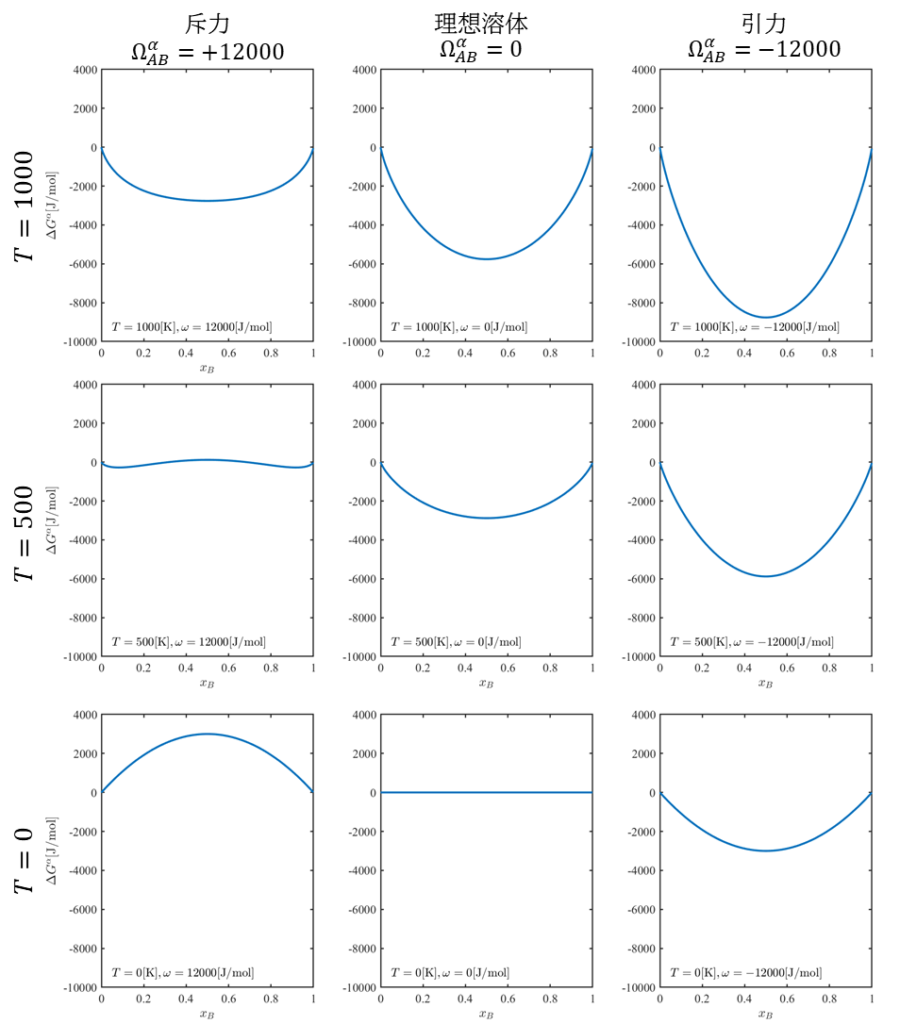
上図より、\(T=1000\rm{[K]}\)の温度が高いときは下に凸のグラフになっていることが分かります。これは結合エネルギー\(\Omega_{AB}^{\alpha} \)よりも配置エントロピーが支配的であるため、原子A,Bを混合させ、状態数増加させることによりギブスの自由エネルギーを減少させようとしているためと考えられます。この時はいずれも\(x_{B}=0.5\)を最小値に持つため、合金状態が安定であることを示しています。
一方で、温度が低くなると結合エネルギー\(\Omega_{AB}^{\alpha} \)が支配的になります。このとき、\(\Omega_{AB}^{\alpha} >0\)の場合、\(x_{B}=0.5\)に最大値を持ち、上に凸なグラフになります。これは原子AB間には斥力が働き、純金属状態が安定であることを示しています。
逆に\(\Omega_{AB}^{\alpha} <0\)の場合、\(x_{B}=0.5\)を最小値に持ち、下に凸なグラフになります。これは原子AB間には引力が働くき、合金状態が安定であることを示しています。
おわりに
今回は固相(置換型固溶体)のギブスの自由エネルギーの導出とその特徴についてまとめました。ギブスの自由エネルギーの成り立ちを理解できた点が勉強になりました。特に結合エンタルピーと配置エントロピーのバランスで組織状態が決定する正則溶体近似の考え方は面白いと思います。次回は液相のギブスの自由エネルギーの導出から始めたいと思います。
参考文献
[1] 三浦 憲司ら, “見方・考え方 合金状態図”, オーム社, 2003/11/1
[2] 須藤 一ら, “金属組織学 (金属工学標準教科書)”, 丸善, 1972/8/1



コメント