はじめに
前回は2次元アレン-カーン方程式を解き、各パラメーターの影響についてまとめました。これらのパラメーターは定数を取り、組織成長は等方的なものでした。しかしながら、デンドライド成長のような非等方的な組織成長を記述するには界面の異方性によるエネルギー効果を考慮する必要があります。そこで今回は界面異方性を考慮したアレン-カーン方程式を導出します。
界面異方性のエネルギー
以下に結晶内部のイメージ図を示します。表面A、Bで示すように結晶を切る面によって、表面の原子の並び方が異なるため、各面でエネルギーの大きさが異なります。
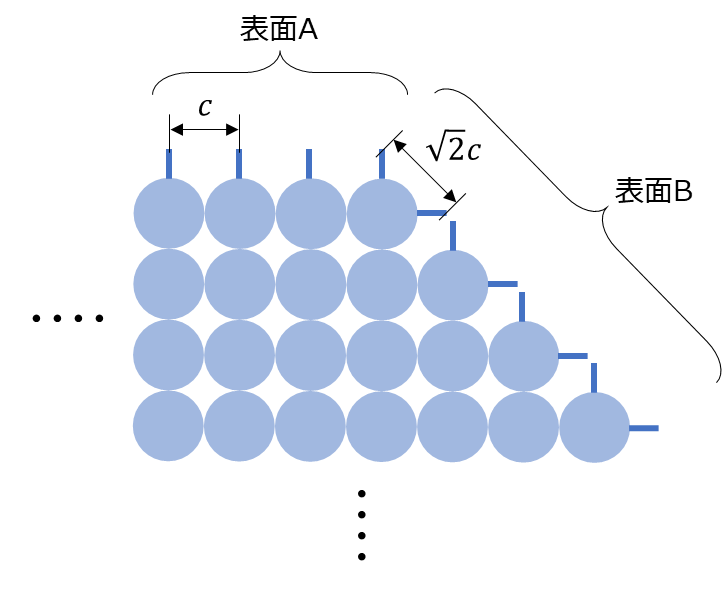
格子定数を\(c\)とすると、表面Aでは結合手が間隔\(c\)で並んでおり、単位長さ当たり\(\frac{1}{c}\)本の結合手があります。一方で、表面Bでは結合手の間隔が\(\sqrt{2}c\)ごとに2本、すなわち、単位長さ当たり\(\frac{2}{\sqrt{2}c}=\frac{\sqrt{2}}{c}\)本の結合手を有しています。したがって、表面Bのほうがより密に結合手を有しており、単純に考えると表面Aの\(\sqrt{2}\)倍の結合エネルギーを有していると言えます。
これまで界面のエネルギーは勾配係数\(a\)の中で、その厚みと曲率のみ考慮してきました。しかしながら実際には上記のように結合エネルギーに由来した界面の向きによるエネルギー依存性(界面異方性)が発生します。
界面法線ベクトル
界面異方性のエネルギーを考えるため、界面方向に依存性する勾配係数\(a(\theta)\)を取り入れます。a相(\(\phi=1\))からb相(\(\phi=0\))へ向かう法線ベクトル\(\boldsymbol{n}\)は次式で与えられます。
\boldsymbol{n} = -\nabla \phi
= –
\begin{pmatrix}
\frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y}
\end{pmatrix}
\tag{1}\\
\end{align}
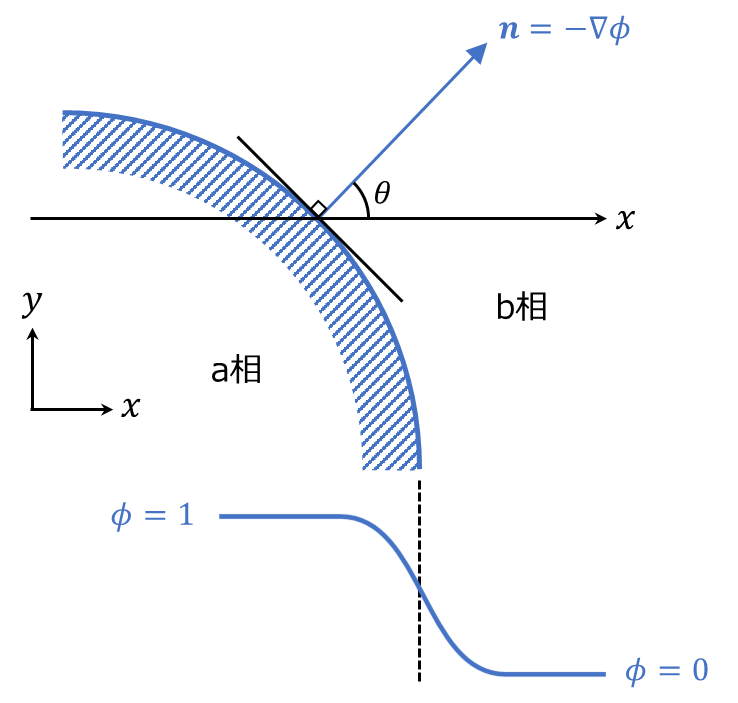
このように法線ベクトルを定義することで、単独相\(\phi=0,1\)ではゼロベクトル、\(0 < \phi < 1\)では有限のベクトルを持たせることが出来ます。
この時、\(x\)軸を基準にとり、\(x\)軸と\(\boldsymbol{n}\)の成す角度を\(\theta\)とすると、次式が成り立ちます。
\theta = \tan^{-1}{\frac{\frac{\partial \phi}{\partial y} }{\frac{\partial \phi}{\partial x} }}
\tag{2}\\
\end{align}
以上より、異方性を考慮した勾配係数\(a(\theta)\)はフェーズフィールド変数\(\phi\)の空間一階微分の関数\(a\left(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y}\right)\)となります。
汎関数微分の計算
\(a\left(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y}\right)\)である場合、汎関数微分の結果に影響を与え、アレン-カーン方程式の形が変化します。汎関数微分形式のアレン-カーン方程式は次式で与えられました。(過去記事参照)
\frac{\partial \phi}{\partial t}&=-M_{\phi}\frac{\delta G}{\delta \phi} \tag{3}\\
G(\phi, \nabla\phi,\nabla ^2\phi)&=\int_V g(\phi, \nabla\phi,\nabla ^2\phi)dV\tag{4}\\
\frac{\delta G}{\delta \phi}&=\frac{\partial g}{\partial \phi}
-\nabla \cdot
\left(\frac{\partial g}{\partial \left(\nabla \phi\right)}\right)
-\nabla ^2
\left(
\frac{\partial g}{\partial \left(\nabla ^2 \phi\right)}\right)
\tag{5}\\
g&=g_{chem}+g_{doub}+g_{grad}\tag{6}\\
g_{chem}&=p(\phi)g_{a}+(1-p(\phi))g_{b}\tag{7}\\
g_{doub}&=Wq(\phi)\tag{8}\\
g_{grad}&=\frac{a^2}{2}(\nabla \phi)^2\tag{9}\\
p(\phi)&=\phi ^2(3-2\phi) \tag{10}\\
q(\phi)&=\phi ^2 (1-\phi)^2 \tag{11}
\end{align}
式\((5)\)の右辺の各項を計算していきましょう。右辺第一項と第三項はこれまでと同様に次のように計算できます。
\frac{\partial g}{\partial \phi}&=\frac{\partial }{\partial \phi}\left(p(\phi)g_{a}+(1-p(\phi))g_{b}+Wq(\phi)\right)\\
&=g_{a}\frac{\partial p(\phi)}{\partial \phi}-g_{b}\frac{\partial p(\phi)}{\partial \phi}+W\frac{\partial q(\phi)}{\partial \phi}\\
&=\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}+W\frac{\partial q(\phi)}{\partial \phi}\tag{12}
\end{align}
\nabla ^2
\left(
\frac{\partial g}{\partial \left(\nabla ^2 \phi\right)}\right)=0
\tag{13}
\end{align}
これまでと異なるのは式\((5)\)右辺第二項の扱いです。勾配係数\(a\)が\(\left(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y}\right)\)の関数となるため、単純に\(\nabla\)の外に出せなくなります。
成分表示にして実際に計算していきます。
\nabla \cdot\left(\frac{\partial g}{\partial \left(\nabla \phi\right)}\right)&=\nabla \cdot\frac{\partial }{\partial \left(\nabla \phi\right)}\left(\frac{a^2}{2}(\nabla \phi)^2\right)\\
&=
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\frac{\partial }{\partial \left(\frac{\partial \phi }{\partial x} \right)} \\ \frac{\partial \phi }{\partial \left(\frac{\partial \phi }{\partial y} \right)}
\end{pmatrix}
\frac{a^2}{2}\left[\left( \frac{\partial \phi}{\partial x}\right)^2+\left(\frac{\partial \phi}{\partial y}\right)^2\right]\\
&=
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\frac{1}{2}\frac{\partial a^2 }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left[\left( \frac{\partial \phi}{\partial x}\right)^2+\left(\frac{\partial \phi}{\partial y}\right)^2\right]+a^2 \frac{\partial \phi }{\partial x}
\\
\frac{1}{2}\frac{\partial a^2 }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left[\left( \frac{\partial \phi}{\partial x}\right)^2+\left(\frac{\partial \phi}{\partial y}\right)^2\right]+a^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}
\\
&=
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\frac{1}{2}\frac{\partial a^2 }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial x}
\\
\frac{1}{2}\frac{\partial a^2 }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}
\\
&=
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\frac{1}{2}\frac{\partial a^2 }{\partial a } \frac{\partial a }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial x}
\\
\frac{1}{2}\frac{\partial a^2 }{\partial a } \frac{\partial a }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}
\\
&=
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
a \frac{\partial a }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial x}
\\
a\frac{\partial a }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}
\tag{14}
\end{align}
ここで、式\((2)\)より
\frac{\partial \left(\frac{\partial \phi }{\partial x}\right) }{\partial \theta }
&=\frac{\partial }{\partial \theta }\left( \frac{\frac{\partial \phi }{\partial y}}{\tan \theta}\right)\\
&=\frac{\partial \phi }{\partial y}\left( \frac{-\frac{1}{\cos^2 \theta}}{\tan^2 \theta}\right)\\
&=-\frac{\frac{\partial \phi }{\partial y}}{\sin^2 \theta}\\
&=-\frac{\frac{\partial \phi }{\partial y}}{\left(\frac{\frac{\partial \phi}{\partial y}}{\left[\left(\frac{\partial \phi }{\partial x}\right)^2+\left(\frac{\partial \phi }{\partial y}\right)^2\right]^\frac{1}{2}}\right)^2}\\
&=-\frac{\left(\nabla \phi\right)^2 }{\frac{\partial \phi }{\partial y}}\\
\rightarrow
\frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial x}\right) }&=-\frac{\frac{\partial \phi }{\partial y}}{\left(\nabla \phi\right)^2 }
\tag{15}\\
\end{align}
同様に、
\frac{\partial \left(\frac{\partial \phi }{\partial y}\right) }{\partial \theta }
&=\frac{\partial }{\partial \theta }\left(\frac{\partial \phi }{\partial x}\tan \theta\right)\\
&=\frac{\frac{\partial \phi }{\partial x}}{\cos^2 \theta}\\
&=\frac{\frac{\partial \phi }{\partial x}}{\left(\frac{\frac{\partial \phi}{\partial x}}{\left[\left(\frac{\partial \phi }{\partial x}\right)^2+\left(\frac{\partial \phi }{\partial y}\right)^2\right]^\frac{1}{2}}\right)^2}\\
&=\frac{\left(\nabla \phi\right)^2 }{\frac{\partial \phi }{\partial x}}\\
\rightarrow
\frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial y}\right) }&=\frac{\frac{\partial \phi }{\partial x}}{\left(\nabla \phi\right)^2 }
\tag{16}\\
\end{align}
以上、式\((15),(16)\)を式\((14)\)に代入すると、式\((5)\)右辺第二項は次のように書けます。
\nabla \cdot\left(\frac{\partial g}{\partial \left(\nabla \phi\right)}\right)
&=
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
a \frac{\partial a }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial x}
\\
a\frac{\partial a }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}\\
&=
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
-a \frac{\partial a }{\partial \theta }\frac{\frac{\partial \phi }{\partial y}}{\left(\nabla \phi\right)^2 } \left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial x}
\\
a\frac{\partial a }{\partial \theta } \frac{\frac{\partial \phi }{\partial x}}{\left(\nabla \phi\right)^2 }\left(\nabla \phi\right)^2+a^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}\\
&=
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
-a \frac{\partial a }{\partial \theta }\frac{\partial \phi }{\partial y} +a^2 \frac{\partial \phi }{\partial x}
\\
a\frac{\partial a }{\partial \theta } \frac{\partial \phi }{\partial x}+a^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}\\
&=
\frac{\partial }{\partial x}
\left(
-a \frac{\partial a }{\partial \theta }\frac{\partial \phi }{\partial y} +a^2 \frac{\partial \phi }{\partial x}
\right)
+
\frac{\partial }{\partial y}
\left(
a\frac{\partial a }{\partial \theta } \frac{\partial \phi }{\partial x}+a^2 \frac{\partial \phi }{\partial y}
\right)\\
&=
\frac{\partial }{\partial x} \left(a^2 \frac{\partial \phi }{\partial x}\right)
+\frac{\partial }{\partial y} \left(a^2 \frac{\partial \phi }{\partial y}\right)
– \frac{\partial }{\partial x}\left( a\frac{\partial a }{\partial \theta }\frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\frac{\partial a }{\partial \theta } \frac{\partial \phi }{\partial x}
\right)\\
&=
\left(2a\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+a^2\frac{\partial ^2\phi}{\partial x^2} \right)
+\left(2a\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y}+a^2\frac{\partial ^2\phi}{\partial y^2} \right)\\
&\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad- \frac{\partial }{\partial x}\left( a\frac{\partial a }{\partial \theta }\frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\frac{\partial a }{\partial \theta } \frac{\partial \phi }{\partial x}
\right)\\
&=
2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)
+a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)\\
&\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad- \frac{\partial }{\partial x}\left( a\frac{\partial a }{\partial \theta }\frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\frac{\partial a }{\partial \theta } \frac{\partial \phi }{\partial x}
\right)
\tag{17}
\end{align}
以上、式\((12),(13),(17)\)を式\((3),(5)\)に代入すると、界面異方性を考慮したアレン-カーン方程式は次のように書けます。
\frac{\partial \phi}{\partial t}&=-M_{\phi}\left[\frac{\partial g}{\partial \phi}
-\nabla \cdot
\left(\frac{\partial g}{\partial \left(\nabla \phi\right)}\right)
-\nabla ^2
\left(
\frac{\partial g}{\partial \left(\nabla ^2 \phi\right)}\right)\right] &\\
&=-M_{\phi}\left[\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}+W\frac{\partial q(\phi)}{\partial \phi}
-2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)\right.\\
&\left.\quad\quad\quad\quad\quad\quad-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
+\frac{\partial }{\partial x}\left( a\frac{\partial a }{\partial \theta }\frac{\partial \phi }{\partial y}
\right)-
\frac{\partial }{\partial y}
\left(
a\frac{\partial a }{\partial \theta } \frac{\partial \phi }{\partial x}
\right)
\right] \tag{18}
\end{align}
しかしながら上式はまだ完成ではありません。右辺の\(\frac{\partial a }{\partial \theta }\)を計算するため、\(a(\theta)\)の具体的な形を決める必要があります。
勾配係数の界面異方性モデル
\(a(\theta)\)は一般に次式で定義されます。
a(\theta)=\bar{a}\left[1+\xi \cos \left\{ k\left( \theta -\theta _0\right)\right\} \right]
\tag{19}
\end{align}
ここで\(\bar{a}\)は基準となる勾配係数、\(\xi\)は異方性の強さを表す異方性強度、\(k\)は異方性の周期性を表す異方性モード、\(\theta _0\)はデンドライドが成長する方向を決めるパラメーターです。式\((19)\)に関してグラフ化し、各パラメーターが波形に与える影響を確認してみましょう。
まず基準となる勾配係数\(\bar{a}\)について\(\bar{a}=1,2,3\)と変えた場合、以下のグラフが得られます。
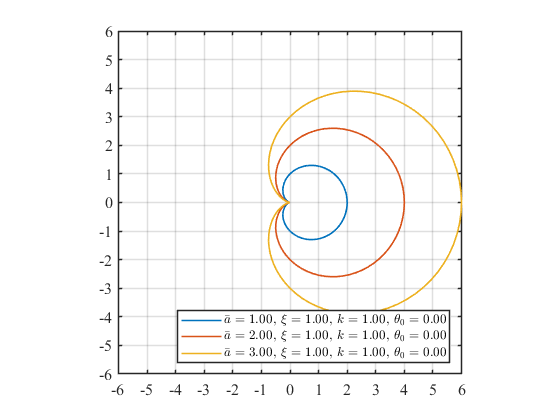
\(\bar{a}\)を大きくすることで、波形全体が大きくなっていく様子が確認できます。したがって、\(\bar{a}\)は振幅をスケール倍する効果があることが分かります。
次に異方性強度\(\xi\)について\(\xi=0,1,2\)と変えた場合、以下のグラフが得られます。
\(\xi\)が大きくなるとともに、\(\theta =0 \)方向の異方性も大きくなっていく様子が確認できます。したがって、\(\xi\)は異方性を強める働きがあることが分かります。
次に異方性モード\(k\)について\(k=1,2,3\)と変えた場合、以下のグラフが得られます。
\(k\)が大きくなるとともに、周期が短くなり、複数の方向で異方性が見られるようになります。したがって、\(k\)は異方性の次数を上げる働きがあることが分かります。
最後に\(\theta _0=0,\frac{\pi}{2},\pi\)とした場合、以下のグラフが得られます。
\(\theta _ 0\)が大きくなるとともに、波形の方向が90度ずつずれていく様子が確認できます。したがって、\(\theta _ 0\)は異方性の方向を変える働きがあることが分かります。
以上で各パラメーターが\(a(\theta)\)に与える影響が分かりました。
界面異方性を考慮したアレン-カーン方程式
式\((19)\)より式\((18)\)における\(\frac{\partial a }{\partial \theta }\)は次のように計算できます。
\frac{\partial a }{\partial \theta }&=\frac{\partial }{\partial \theta }\left(\bar{a}\left[1+\xi \cos \left\{ k\left( \theta -\theta _0\right)\right\} \right]\right)\\
&=-\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\}
\tag{20}
\end{align}
上式を式\((18)\)に代入すると
\frac{\partial \phi}{\partial t}&=-M_{\phi}\left[\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}+W\frac{\partial q(\phi)}{\partial \phi}
-2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)\right.\\
&\left.\quad\quad\quad\quad\quad-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
+\frac{\partial }{\partial x}\left( a\frac{\partial a }{\partial \theta }\frac{\partial \phi }{\partial y}
\right)-
\frac{\partial }{\partial y}
\left(
a\frac{\partial a }{\partial \theta } \frac{\partial \phi }{\partial x}
\right)
\right] \\
&=-M_{\phi}\left[\left(g_{a}-g_{b}\right)\frac{\partial p(\phi)}{\partial \phi}+W\frac{\partial q(\phi)}{\partial \phi}
-2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)\right.\\
&\left. \quad\quad\quad\quad\quad-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
-\frac{\partial }{\partial x}\left( a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial y}
\right)\right.\\
&\left.\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad+
\frac{\partial }{\partial y}
\left(
a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial x}
\right)
\right]
\tag{21}
\end{align}
過去の記事より、式\((10),(11)\)を用いると、次式が成り立ちます。
\frac{\partial p(\phi)}{\partial \phi} &=6\phi\left(1-\phi\right) \tag{22}\\
\frac{\partial q(\phi)}{\partial \phi} &= 2\phi (1-\phi)(1-2\phi) \tag{23}\\
\end{align}
これらを式\((21)\)に代入すると、最終的に界面異方性を考慮したアレン-カーン方程式は次のように書けます。
\frac{\partial \phi}{\partial t}&=-M_{\phi}\left[6\left(g_{a}-g_{b}\right)\phi\left(1-\phi\right)+2W\phi (1-\phi)(1-2\phi)
\right.\\
&\left. \quad\quad\quad\quad\quad-2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
\right.\\
&\left.\quad\quad\quad\quad\quad\quad
-\frac{\partial }{\partial x}\left( a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial x}
\right)
\right]
\tag{24}
\end{align}
結構複雑な式になってしまいましたね…。この後上式を離散化していきますが、長くなってきたので次回の記事に持ち越したいと思います。
おわりに
今回は界面異方性を考慮したアレン-カーン方程式を導出しました。はじめは勾配係数\(a\)を\(\theta\)の関数として考えるだけかと思っていましたが、実際に導出してみると意外とややこしいことが分かりました。次回は式\((24)\)を離散化し、シミュレーションしてみたいと思います。
参考文献
[1] 高木 知弘ら, “フェーズフィールド法”, 養賢堂, 2012/3/2
[2] 山中 晃徳ら, “Pythonによるフェーズフィールド法入門 基礎理論からデータ同化の実装まで”, 丸善出版, 2023/12/15



コメント