はじめに
前回は純物質凝固モデルとして以下の温度場を考慮したアレンカーン方程式と相変化による潜熱を考慮した非定常熱伝導方程式を得ました。
\begin{align}
\frac{\partial \phi}{\partial t}&=-M_{\phi}\left[30l\left(\frac{T-T_{m}}{T_{m}}\right)\phi^2\left(1-\phi\right)^2+2W\phi (1-\phi)(1-2\phi)
\right.\\
&\left. \quad\quad\quad\quad\quad-2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
\right.\\
&\left.\quad\quad\quad\quad\quad\quad
-\frac{\partial }{\partial x}\left( a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial x}
\right)
\right]
\tag{1}\\
c_{v}\frac{\partial T}{\partial t} &= K\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right) + 30l\phi ^2(1-\phi)^2\frac{\partial \phi}{\partial t}\tag{2}
\end{align}
\frac{\partial \phi}{\partial t}&=-M_{\phi}\left[30l\left(\frac{T-T_{m}}{T_{m}}\right)\phi^2\left(1-\phi\right)^2+2W\phi (1-\phi)(1-2\phi)
\right.\\
&\left. \quad\quad\quad\quad\quad-2a\left(\frac{\partial a}{\partial x} \frac{\partial \phi }{\partial x}+\frac{\partial a}{\partial y} \frac{\partial \phi }{\partial y} \right)-a^2\left(\frac{\partial ^2\phi}{\partial x^2}+\frac{\partial ^2\phi}{\partial y^2} \right)
\right.\\
&\left.\quad\quad\quad\quad\quad\quad
-\frac{\partial }{\partial x}\left( a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
a\bar{a}k\xi \sin \left\{ k\left( \theta -\theta _0\right)\right\} \frac{\partial \phi }{\partial x}
\right)
\right]
\tag{1}\\
c_{v}\frac{\partial T}{\partial t} &= K\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right) + 30l\phi ^2(1-\phi)^2\frac{\partial \phi}{\partial t}\tag{2}
\end{align}
今回はこれらを離散化し、実際に計算してみたいと思います。
温度場を考慮したアレン-カーン方程式の離散化
まずアレン-カーン方程式\((1)\)について離散化します。基本的には界面異方性を考慮した場合と同様ですが温度場が含まれることに注意します。
\begin{align}
\frac{\phi_{i,j}^{n+1}-\phi_{i,j}^{n}}{\Delta t}&=-M_{\phi}\left[6l\left(\frac{T_{i,j}^{n}-T_{m}}{T_{m}}\right)\phi_{i,j}^{n}\left(1-\phi_{i,j}^{n}\right)+2W\phi_{i,j}^{n} (1-\phi_{i,j}^{n})(1-2\phi_{i,j}^{n})
\right.\\
&\left. \quad\quad\quad\quad\quad-2a_{i,j}^{n}\left(\frac{a_{i+1,j}^{n}-a_{i-1,j}^{n}}{2\Delta x} \frac{ \phi_{i+1,j}^{n}-\phi_{i-1,j}^{n} }{2\Delta x}+\frac{a_{i,j+1}^{n}-a_{i,j-1}^{n}}{2\Delta y} \frac{\phi_{i,j+1}^{n}-\phi_{i,j-1}^{n} }{2\Delta y} \right)\\
\quad\quad-\left(a_{i,j}^{n}\right)^2\Delta^9\phi_{i,j}^{n}
-\frac{A_{i+1,j}^{n}-A_{i-1,j}^{n} }{2\Delta x}+
\frac{B_{i,j+1}^{n}-B_{i,j-1}^{n} }{2\Delta y}
\right] \\
\rightarrow
\phi_{i,j}^{n+1}&=\phi_{i,j}^{n}+M_{\phi}\Delta t\left[-6l\left(\frac{T_{i,j}^{n}-T_{m}}{T_{m}}\right)\phi_{i,j}^{n}\left(1-\phi_{i,j}^{n}\right)-2W\phi_{i,j}^{n} (1-\phi_{i,j}^{n})(1-2\phi_{i,j}^{n})
\right.\\
&\left. \quad\quad\quad\quad\quad+2a_{i,j}^{n}\left(\frac{a_{i+1,j}^{n}-a_{i-1,j}^{n}}{2\Delta x} \frac{ \phi_{i+1,j}^{n}-\phi_{i-1,j}^{n} }{2\Delta x}+\frac{a_{i,j+1}^{n}-a_{i,j-1}^{n}}{2\Delta y} \frac{\phi_{i,j+1}^{n}-\phi_{i,j-1}^{n} }{2\Delta y} \right)\\
\quad\quad+\left(a_{i,j}^{n}\right)^2\Delta^9\phi_{i,j}^{n}+\frac{A_{i+1,j}^{n}-A_{i-1,j}^{n} }{2\Delta x}-
\frac{B_{i,j+1}^{n}-B_{i,j-1}^{n} }{2\Delta y}
\right] \tag{3}\\
A_{i,j}^{n}&=a_{i,j}^{n}\bar{a}k\xi \sin \left\{ k\left( \theta_{i,j}^{n} -\theta _0\right)\right\} \frac{\phi_{i,j+1}^{n}-\phi_{i,j-1}^{n} }{2\Delta y} \tag{4}\\
B_{i,j}^{n}&=a_{i,j}^{n}\bar{a}k\xi \sin \left\{ k\left( \theta_{i,j}^{n} -\theta _0\right)\right\} \frac{\phi_{i+1,j}^{n}-\phi_{i-1,j}^{n} }{2\Delta x}\tag{5}\\
a_{i,j}^{n}&=\bar{a}\left[1+\xi \cos \left\{ k\left( \theta_{i,j}^{n} -\theta _0\right)\right\} \right]
\tag{6}
\end{align}
\frac{\phi_{i,j}^{n+1}-\phi_{i,j}^{n}}{\Delta t}&=-M_{\phi}\left[6l\left(\frac{T_{i,j}^{n}-T_{m}}{T_{m}}\right)\phi_{i,j}^{n}\left(1-\phi_{i,j}^{n}\right)+2W\phi_{i,j}^{n} (1-\phi_{i,j}^{n})(1-2\phi_{i,j}^{n})
\right.\\
&\left. \quad\quad\quad\quad\quad-2a_{i,j}^{n}\left(\frac{a_{i+1,j}^{n}-a_{i-1,j}^{n}}{2\Delta x} \frac{ \phi_{i+1,j}^{n}-\phi_{i-1,j}^{n} }{2\Delta x}+\frac{a_{i,j+1}^{n}-a_{i,j-1}^{n}}{2\Delta y} \frac{\phi_{i,j+1}^{n}-\phi_{i,j-1}^{n} }{2\Delta y} \right)\\
\quad\quad-\left(a_{i,j}^{n}\right)^2\Delta^9\phi_{i,j}^{n}
-\frac{A_{i+1,j}^{n}-A_{i-1,j}^{n} }{2\Delta x}+
\frac{B_{i,j+1}^{n}-B_{i,j-1}^{n} }{2\Delta y}
\right] \\
\rightarrow
\phi_{i,j}^{n+1}&=\phi_{i,j}^{n}+M_{\phi}\Delta t\left[-6l\left(\frac{T_{i,j}^{n}-T_{m}}{T_{m}}\right)\phi_{i,j}^{n}\left(1-\phi_{i,j}^{n}\right)-2W\phi_{i,j}^{n} (1-\phi_{i,j}^{n})(1-2\phi_{i,j}^{n})
\right.\\
&\left. \quad\quad\quad\quad\quad+2a_{i,j}^{n}\left(\frac{a_{i+1,j}^{n}-a_{i-1,j}^{n}}{2\Delta x} \frac{ \phi_{i+1,j}^{n}-\phi_{i-1,j}^{n} }{2\Delta x}+\frac{a_{i,j+1}^{n}-a_{i,j-1}^{n}}{2\Delta y} \frac{\phi_{i,j+1}^{n}-\phi_{i,j-1}^{n} }{2\Delta y} \right)\\
\quad\quad+\left(a_{i,j}^{n}\right)^2\Delta^9\phi_{i,j}^{n}+\frac{A_{i+1,j}^{n}-A_{i-1,j}^{n} }{2\Delta x}-
\frac{B_{i,j+1}^{n}-B_{i,j-1}^{n} }{2\Delta y}
\right] \tag{3}\\
A_{i,j}^{n}&=a_{i,j}^{n}\bar{a}k\xi \sin \left\{ k\left( \theta_{i,j}^{n} -\theta _0\right)\right\} \frac{\phi_{i,j+1}^{n}-\phi_{i,j-1}^{n} }{2\Delta y} \tag{4}\\
B_{i,j}^{n}&=a_{i,j}^{n}\bar{a}k\xi \sin \left\{ k\left( \theta_{i,j}^{n} -\theta _0\right)\right\} \frac{\phi_{i+1,j}^{n}-\phi_{i-1,j}^{n} }{2\Delta x}\tag{5}\\
a_{i,j}^{n}&=\bar{a}\left[1+\xi \cos \left\{ k\left( \theta_{i,j}^{n} -\theta _0\right)\right\} \right]
\tag{6}
\end{align}
ここで\(\theta_{i,j}^{n}\)は時間・空間分布を有し、次式のように法線ベクトル\(\boldsymbol{n}_{i,j}^{n}\)の向きに応じて計算式が変化します。
\begin{align}
\theta_{i,j}^{n}&=
\begin{cases}
\tan ^{-1}\left(\frac{ny_{i,j}^{n}}{nx_{i,j}^{n}}\right) & nx_{i,j}^{n}> 0かつny_{i,j}^{n}> 0の場合\\
\tan ^{-1}\left(\frac{ny_{i,j}^{n}}{nx_{i,j}^{n}}\right) +\pi & nx_{i,j}^{n}< 0かつny_{i,j}^{n}> 0の場合\\
\tan ^{-1}\left(\frac{ny_{i,j}^{n}}{nx_{i,j}^{n}}\right) +\pi & nx_{i,j}^{n}< 0かつny_{i,j}^{n}< 0の場合\\
\tan ^{-1}\left(\frac{ny_{i,j}^{n}}{nx_{i,j}^{n}}\right) +2\pi & nx_{i,j}^{n}> 0かつny_{i,j}^{n}< 0の場合\\
0 & nx_{i,j}^{n}> 0かつny_{i,j}^{n}= 0の場合\\
\frac{\pi}{2} & nx_{i,j}^{n}= 0かつny_{i,j}^{n}> 0の場合\\
\pi & nx_{i,j}^{n}< 0かつny_{i,j}^{n}= 0の場合\\
\frac{3\pi}{2} & nx_{i,j}^{n}=0かつny_{i,j}^{n}< 0の場合\\
\end{cases}
\tag{7}\\
\boldsymbol{n}_{i,j}^{n}
&=
\begin{pmatrix}
nx_{i,j}^{n} \\ ny_{i,j}^{n}
\end{pmatrix}
= -\nabla \phi
= –
\begin{pmatrix}
\frac{\phi_{i+1,j}^{n}-\phi_{i-1,j}^{n}}{2\Delta x} \\ \frac{\phi_{i,j+1}^{n}-\phi_{i,j-1}^{n}}{2\Delta y}
\end{pmatrix}
\tag{8}
\end{align}
\theta_{i,j}^{n}&=
\begin{cases}
\tan ^{-1}\left(\frac{ny_{i,j}^{n}}{nx_{i,j}^{n}}\right) & nx_{i,j}^{n}> 0かつny_{i,j}^{n}> 0の場合\\
\tan ^{-1}\left(\frac{ny_{i,j}^{n}}{nx_{i,j}^{n}}\right) +\pi & nx_{i,j}^{n}< 0かつny_{i,j}^{n}> 0の場合\\
\tan ^{-1}\left(\frac{ny_{i,j}^{n}}{nx_{i,j}^{n}}\right) +\pi & nx_{i,j}^{n}< 0かつny_{i,j}^{n}< 0の場合\\
\tan ^{-1}\left(\frac{ny_{i,j}^{n}}{nx_{i,j}^{n}}\right) +2\pi & nx_{i,j}^{n}> 0かつny_{i,j}^{n}< 0の場合\\
0 & nx_{i,j}^{n}> 0かつny_{i,j}^{n}= 0の場合\\
\frac{\pi}{2} & nx_{i,j}^{n}= 0かつny_{i,j}^{n}> 0の場合\\
\pi & nx_{i,j}^{n}< 0かつny_{i,j}^{n}= 0の場合\\
\frac{3\pi}{2} & nx_{i,j}^{n}=0かつny_{i,j}^{n}< 0の場合\\
\end{cases}
\tag{7}\\
\boldsymbol{n}_{i,j}^{n}
&=
\begin{pmatrix}
nx_{i,j}^{n} \\ ny_{i,j}^{n}
\end{pmatrix}
= -\nabla \phi
= –
\begin{pmatrix}
\frac{\phi_{i+1,j}^{n}-\phi_{i-1,j}^{n}}{2\Delta x} \\ \frac{\phi_{i,j+1}^{n}-\phi_{i,j-1}^{n}}{2\Delta y}
\end{pmatrix}
\tag{8}
\end{align}
また今回、ラプラシアンの計算には、文献[２]に基づき、以下の9点ラプラシアン\(\Delta^{9}\)を用います。
\begin{align}
\Delta^{9}\phi_{i,j}^{n}=\frac{2\left(\phi_{i-1,j}^{n}+\phi_{i,j-1}^{n}+\phi_{i+1,j}^{n}+\phi_{i,j+1}^{n}\right)+\left(\phi_{i-1,j-1}^{n}+\phi_{i+1,j+1}^{n}+\phi_{i-1,j+1}^{n}+\phi_{i+1,j-1}^{n}\right)-12\phi_{i,j}^{n}}{3h^2}\tag{9}
\end{align}
\Delta^{9}\phi_{i,j}^{n}=\frac{2\left(\phi_{i-1,j}^{n}+\phi_{i,j-1}^{n}+\phi_{i+1,j}^{n}+\phi_{i,j+1}^{n}\right)+\left(\phi_{i-1,j-1}^{n}+\phi_{i+1,j+1}^{n}+\phi_{i-1,j+1}^{n}+\phi_{i+1,j-1}^{n}\right)-12\phi_{i,j}^{n}}{3h^2}\tag{9}
\end{align}
ここで\(h=dx=dy\)を想定しています。
通常のラプラシアンは上下左右・中央の5点のステンシルを用いますが、9点ラプラシアンではそれに加えて、斜め方向のステンシルも用います。これにより曲面の評価精度を向上させることが出来るようです。上式の出典を見つけることはできなかったのですが、こちら[3]などが近い話なのかと思います。
以上が温度場を考慮したアレン-カーン方程式の離散化形式です。
潜熱を考慮した熱伝導方程式の離散化
次に相変化による潜熱を考慮した熱伝導方程式\((2)\)について離散化を行います。アレン-カーン方程式\((1)\)と同様に左辺の時間微分はオイラー陽解法、右辺の空間微分は9点ラプラシアンを利用します。
\begin{align}
c_{v}\frac{T_{i,j}^{n+1}-T_{i,j}^{n}}{\Delta t} &= K\Delta ^9 T_{i,j}^{n} + 6l\phi _{i,j}^{n} (1-\phi_{i,j}^{n})\frac{\phi _{i,j}^{n+1}-\phi _{i,j}^{n}}{\Delta t}\\
\rightarrow
T_{i,j}^{n+1}&=T_{i,j}^{n}+\frac{\Delta t}{c_{v}} \left[K\Delta ^9 T_{i,j}^{n}+ 6l\phi _{i,j}^{n} (1-\phi_{i,j}^{n})\frac{\phi _{i,j}^{n+1}-\phi _{i,j}^{n}}{\Delta t}\right]
\tag{10}
\end{align}
c_{v}\frac{T_{i,j}^{n+1}-T_{i,j}^{n}}{\Delta t} &= K\Delta ^9 T_{i,j}^{n} + 6l\phi _{i,j}^{n} (1-\phi_{i,j}^{n})\frac{\phi _{i,j}^{n+1}-\phi _{i,j}^{n}}{\Delta t}\\
\rightarrow
T_{i,j}^{n+1}&=T_{i,j}^{n}+\frac{\Delta t}{c_{v}} \left[K\Delta ^9 T_{i,j}^{n}+ 6l\phi _{i,j}^{n} (1-\phi_{i,j}^{n})\frac{\phi _{i,j}^{n+1}-\phi _{i,j}^{n}}{\Delta t}\right]
\tag{10}
\end{align}
右辺の\(\phi _{i,j}^{n+1}\)には、式\((3)\)で求めた値を用います。
以上が潜熱を考慮した熱伝導方程式の離散化形式です。
計算フロー
計算フローは以下の通りです。始めにフェーズフィールド変数を解き、それに基づき温度場を解きます。
安定性条件
フェーズフィールド変数の時間発展式\((3)\)の解の安定性条件は、\(M_{\phi}a^2\)を拡散係数と見立てて、以下のように与えられました。（過去記事参照）
\begin{align}
\Delta t_{1}\leq \frac{1}{2M_{\phi}\cdot\max(a)^2}\frac{\left(\Delta x\right)^2\left(\Delta y\right)^2}{\left(\Delta x\right)^2+\left(\Delta y\right)^2}\tag{11}
\end{align}
\Delta t_{1}\leq \frac{1}{2M_{\phi}\cdot\max(a)^2}\frac{\left(\Delta x\right)^2\left(\Delta y\right)^2}{\left(\Delta x\right)^2+\left(\Delta y\right)^2}\tag{11}
\end{align}
今回は上記に加え、温度場の時間発展式\((9)\)も解くため、これに関する安定性条件も加わります。式\((9)\)において、拡散係数は\(\frac{K}{c_{v}}\)に相当します。したがって、安定性条件としては以下のように書けます。
\begin{align}
\Delta t_{2}\leq \frac{c_{v}}{2K}\frac{\left(\Delta x\right)^2\left(\Delta y\right)^2}{\left(\Delta x\right)^2+\left(\Delta y\right)^2}\tag{12}
\end{align}
\Delta t_{2}\leq \frac{c_{v}}{2K}\frac{\left(\Delta x\right)^2\left(\Delta y\right)^2}{\left(\Delta x\right)^2+\left(\Delta y\right)^2}\tag{12}
\end{align}
以上、\(\Delta t_{1}, \Delta t_{2}\)のうち、より厳しい条件を満たすように、タイムステップを決めればよいでしょう。
解析条件
今回はNi原子の凝固現象を対象とします。Ni原子の物性パラメーターは以下のとおりです。
\begin{align}
\begin{array}{ccc}
\hline
\textbf{Ni Property} & \textbf{value} & \textbf{units}\\
\hline
融点 T_{m} & 1728 & \rm{[K]} \\
界面エネルギー \gamma & 0.37 & \rm{[J/m^2]} \\
熱伝導率 K & 84.01 & \rm{[W/m⋅K]} \\
体積比熱 c_{v} & 5.42 \times 10^{6} & \rm{ [J/K⋅m^3]} \\
潜熱密度 l & 2.35 \times 10^{9} & \rm{[J/mol]}\\
界面カイネティック係数 \mu & 2.0 & \rm{[m/(K⋅s)]}\\
\hline
\end{array}
\end{align}
\begin{array}{ccc}
\hline
\textbf{Ni Property} & \textbf{value} & \textbf{units}\\
\hline
融点 T_{m} & 1728 & \rm{[K]} \\
界面エネルギー \gamma & 0.37 & \rm{[J/m^2]} \\
熱伝導率 K & 84.01 & \rm{[W/m⋅K]} \\
体積比熱 c_{v} & 5.42 \times 10^{6} & \rm{ [J/K⋅m^3]} \\
潜熱密度 l & 2.35 \times 10^{9} & \rm{[J/mol]}\\
界面カイネティック係数 \mu & 2.0 & \rm{[m/(K⋅s)]}\\
\hline
\end{array}
\end{align}
またメッシュ数等、その他計算パラメーターは下表のとおり設定します。
\begin{align}
\begin{array}{ccc}
\hline
\textbf{calculation parameters} & \textbf{value} & \textbf{units}\\
\hline
メッシュ数 n_{x},n_{y} & 750 & \rm{[-]} \\
メッシュサイズ dx,dy & 2.0\times10^{-8} & \rm{[m]} \\
タイムステップ dt & 5.0\times10^{-12}& \rm{[s]} \\
界面幅 \delta & 4dx & \rm{[m]} \\
異方性強度 \xi & 0.03 & \rm{ [-]} \\
異方性モード k & 4 & \rm{[-]}\\
優先成長方向 \theta_0 & 0 & \rm{[deg]}\\
\hline
\end{array}
\end{align}
\begin{array}{ccc}
\hline
\textbf{calculation parameters} & \textbf{value} & \textbf{units}\\
\hline
メッシュ数 n_{x},n_{y} & 750 & \rm{[-]} \\
メッシュサイズ dx,dy & 2.0\times10^{-8} & \rm{[m]} \\
タイムステップ dt & 5.0\times10^{-12}& \rm{[s]} \\
界面幅 \delta & 4dx & \rm{[m]} \\
異方性強度 \xi & 0.03 & \rm{ [-]} \\
異方性モード k & 4 & \rm{[-]}\\
優先成長方向 \theta_0 & 0 & \rm{[deg]}\\
\hline
\end{array}
\end{align}
界面の曲率評価を正確に行うため、メッシュ数は多めに\(n_{x}=n_{y}=750\)とします。
このとき、式\((11),(12)\)より\(\Delta t_{1}=1.73\times 10^{-10}, \Delta t_{2}=6.45\times 10^{-12}\)となります。したがって、タイムステップはより条件的に厳しい\(\Delta t_{2}\)を満たすように、\(dt=5.0\times10^{-12}\)としています。
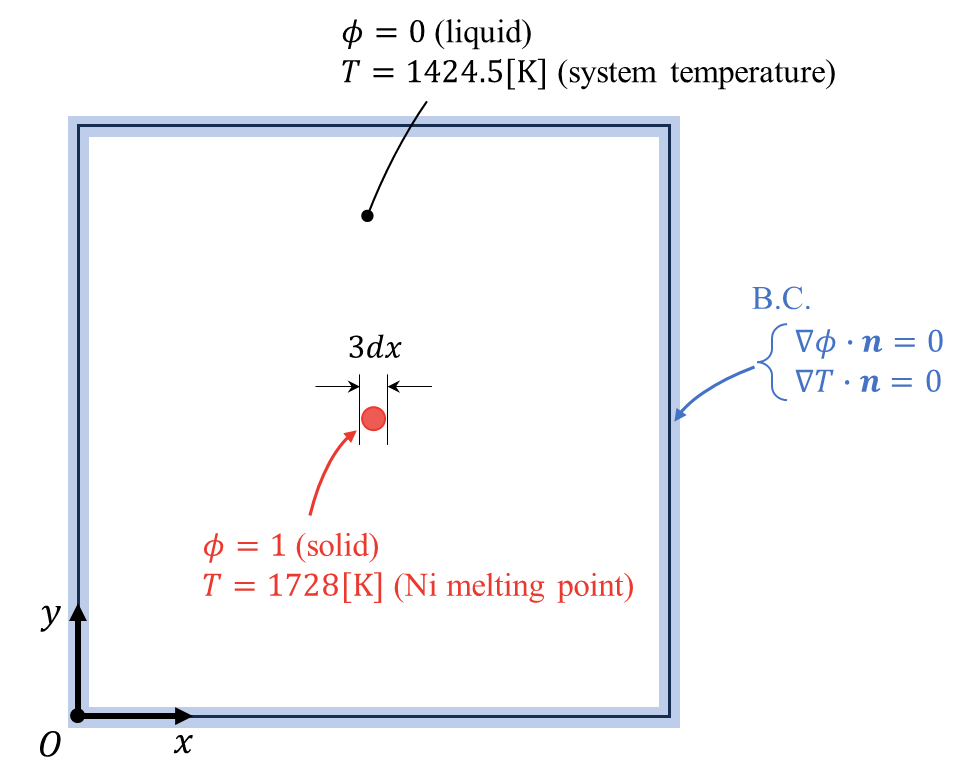
初期条件は、過冷却状態（\(T=1424.5\rm{[K]}\)）の溶融Ni液体（\(\phi=0\)）の中心に、直径\(3dx\)、温度がちょうど融点（\(T=1728\rm{[K]}\)）のNi固体（\(\phi=1\)）の凝固核を配置した状態とします。
また境界条件はフェーズフィールド変数・温度共にノイマン条件を与えることとします。
計算結果
以下に計算結果を示します。左からフェーズフィールド変数、温度場、潜熱を表します。
領域中心に設置した凝固核が時間とともに成長し、デンドライト形状を形成するのが分かります。また、固液界面で潜熱が発生し、デンドライト領域において、温度は融点\(T_{m}\)でほぼ一定となっています。
\(\Delta g =g_{S}−g_{L} =l\frac{T-T_{m}}{T_{m}}\)より\(T<T_{m}\)の時、\(g_{S}<g_{L} \)となり、液相より固相のほうが自由エネルギーが低くなります。したがって、上記のように時間とともに液相領域が縮小し、固相領域が拡大していくと考えられます。
また温度場において、デンドライト形状のような微細な隙間が見られないのが一見不思議です。これはデンドライトの成長より熱の拡散が早いため、温度が比較的早い段階で一定化し、そちら方向への化学的駆動力が失われてしまうためと思われます。
なぜデンドライトのような複雑な形が形成されるのかについては次回記事にて詳細をまとめたいと思います。
MATLABコード
以下に今回使用したMATLABコードを記載します。
% 初期化処理 --------------------------------------------------------------
clc; close all;
clear all;
% パラメーター設定 --------------------------------------------------------
% 時間・空間ステップ設定
dt = 5.0e-12; % タイムステップ[s]
maxstep = 25000; % 最大ステップ数
dx = 2.0e-08; % 差分格子点の間隔[m]:20[um]
dy = dx; % 差分格子点の間隔[m]
nx = 750; % 差分格子点数
ny = nx; % 差分格子点数
xmax = dx * nx ;
xmin = 0;
ymax = dy * ny;
ymin = 0;
xl = xmin:dx:xmax-dx;
yl = ymin:dy:ymax-dy;
% 物性値の設定
T_0 = 1424.5; % 系の温度 [K]
T_melt = 1728.0; % Niの融点 [K]
gamma = 0.37; % 界面エネルギー [J/m2]
K = 84.01; % 熱伝導率 [W/(mK)]
cv = 5.42e+06; % 比熱 [J/K]
latent = 2.35e+09; % 潜熱 [J/mol]
mu = 2.0; % 界面カイネティック係数 [m/(Ks)]
lamb = 0.1; % 界面厚みの閾値
b = 2.0 * atanh(1.0 - 2.0 * lamb);
delta = 4.0 * dx; % 界面幅[m]
kareido = cv *(T_melt-T_0)/latent; % 過冷度
% 物性値の変換
w = 6.0 * gamma * b / delta; % エネルギー障壁[J/m3]
mp = b * T_melt * mu / (3.0 * delta * latent); % フェーズフィールドモビリティー
abar = sqrt(3.0*delta*gamma/b); % 基準となる勾配係数
xi = 0.03; % 異方性強度
k = 4; % 異方性モード
theta_0 = 0; % 優先成長方向
% 変数宣言
phi = zeros(nx,ny);
phi_new = zeros(nx,ny);
dphi = zeros(nx,ny);
q = zeros(nx,ny);
nvec_x = zeros(nx,ny);
nvec_y = zeros(nx,ny);
T = zeros(nx,ny);
dT = zeros(nx,ny);
T_new = zeros(nx,ny);
dg = zeros(nx,ny);
theta = zeros(nx,ny);
thetadeg = zeros(nx,ny);
a = zeros(nx,ny);
A = zeros(nx,ny);
B = zeros(nx,ny);
dadx= zeros(nx,ny);
dady = zeros(nx,ny);
dphidx = zeros(nx,ny);
dphidy = zeros(nx,ny);
lap_phi = zeros(nx,ny);
lap_temp = zeros(nx,ny);
% 安定条件の確認
theta_test = 0:2*pi/100:2*pi;
amax = max(abar * (1 + xi * cos(k*(theta_test-theta_0))));% 勾配係数の最大値を計算する。
dt1 = (1/(2*amax^2*mp))*(dx^2*dy^2)/(dx^2+dy^2);
dt2 =(cv/(2*K))*(dx^2*dy^2)/(dx^2+dy^2);
if dt > min(dt1,dt2)
error('タイムステップが安定条件を満たしていません。')
end
% 可視化設定 -----------------------------------------------------------------
% ファイル名
paramstr =['n = ', num2str(nx, '%.0f'), ', dt = ', num2str(dt, '%.1e'), ...
', mp = ', num2str(mp, '%.2f'), ', xi = ', num2str(xi, '%.2f'),...
', k = ', num2str(k, '%.2f'), ', theta_0 = ', num2str(theta_0, '%.2f')];
filename = [paramstr,'.mp4'];
% VideoWriter オブジェクトの初期化
outputVideo = VideoWriter(filename, 'MPEG-4');
outputVideo.FrameRate = 30; % フレームレートの設定
open(outputVideo);
% グラフの配置調整
figure('Visible', 'off', 'Position', [100, 100, 1800, 600], 'Color', 'white');
ax1 = axes('Position', [0.05, 0.1, 0.28, 0.8]);
ax2 = axes('Position', [0.37, 0.1, 0.28, 0.8]);
ax3 = axes('Position', [0.69, 0.1, 0.28, 0.8]);
[Y, X] = meshgrid(yl, xl); % X, Yグリッドを生成
% レンジの決定
xmin = min(xl);
xmax = max(xl);
ymin = min(yl);
ymax = max(yl);
% テキストボックスのテキスト作成
str_1 = ['$ n_{x} = n_{y} =', num2str(nx, '%.0f'), ...
', \, dt = ', num2str(dt, '%.1e'), ...
', \, \bar{a} = ', num2str(abar, '%.1e'), '$'];
str_2 = ['$ W = ', num2str(mp, '%.1e'), ...
', \, M_p = ', num2str(mp, '%.1f'), ...
', \, \xi = ', num2str(xi, '%.2f'), ...
', \, k = ', num2str(k, '%.1f'), ...
', \, \theta_0 = ', num2str(theta_0, '%.1f'), '$'];
str = {str_1, str_2};
% テキストボックスの位置とサイズを定義
dim1 = [0.06 0.1 0.18 0.12];
dim2 = [0.38 0.1 0.18 0.12];
dim3 = [0.70 0.1 0.18 0.12];
% テキストボックスを図に追加
annotation('textbox', dim1, 'String', str, 'FitBoxToText', 'on', ...
'BackgroundColor', 'none', 'EdgeColor', 'none', 'FontSize', 12, 'Interpreter', 'latex');
annotation('textbox', dim2, 'String', str, 'FitBoxToText', 'on', ...
'BackgroundColor', 'none', 'EdgeColor', 'none', 'FontSize', 12, 'Interpreter', 'latex');
annotation('textbox', dim3, 'String', str, 'FitBoxToText', 'on', ...
'BackgroundColor', 'none', 'EdgeColor', 'none', 'FontSize', 12, 'Interpreter', 'latex');
% 初期条件 ----------------------------------------------------------------
r0 = 2 * dx;
for j = 1 : ny
for i = 1 : nx
%r = sqrt((i*dx)^2 +((ny-j)*dy)^2) - r0;% 原点に核生成
r = sqrt( ((i-(nx/2))*dx)^2 +((j-(ny/2)) * dy)^2 ) - r0;% 中央に核生成
phi(i, j) = 0.5 * (1 - tanh(sqrt(2 * w) / (2 * abar) * r)); % フェーズフィールド変数の初期分布
T(i,j,1) = T_0 + phi(i,j) * (T_melt - T_0); % 温度の初期分布
end
end
% 時間発展 ----------------------------------------------------------------
for step = 1 : maxstep
step
% 界面異方性を考慮した勾配係数計算のループ
for i = 1 : nx
for j = 1 : ny
% 隣接節点
ip = i + 1;
im = i - 1;
jp = j + 1;
jm = j - 1;
% ノイマン条件
if ip > nx
ip = nx;
end
if im < 1
im = 1;
end
if jp > ny
jp = ny;
end
if jm < 1
jm = 1;
end
% 法線ベクトル計算
nvec_x(i,j) = -(phi(ip,j) - phi(im,j))/(2*dx);
nvec_y(i,j) = -(phi(i,jp) - phi(i,jm))/(2*dy);
% 法線ベクトルとX軸が成す角度の計算。基底ベクトルの正負に応じて割り当てる角度範囲を変える。
if nvec_x(i,j)>0 && nvec_y(i,j)>0
theta(i,j) = atan(nvec_y(i,j)/nvec_x(i,j));
elseif nvec_x(i,j)<0 && nvec_y(i,j)>0
theta(i,j) = atan(nvec_y(i,j)/nvec_x(i,j)) + pi;
elseif nvec_x(i,j)<0 && nvec_y(i,j)<0
theta(i,j) = atan(nvec_y(i,j)/nvec_x(i,j)) + pi;
elseif nvec_x(i,j)>0 && nvec_y(i,j)<0
theta(i,j) = atan(nvec_y(i,j)/nvec_x(i,j)) + 2*pi;
elseif nvec_x(i,j)>0 && nvec_y(i,j)==0
theta(i,j) = 0;
elseif nvec_x(i,j)==0 && nvec_y(i,j)>0
theta(i,j) = pi/2;
elseif nvec_x(i,j)<0 && nvec_y(i,j)==0
theta(i,j) = pi;
elseif nvec_x(i,j)==0 && nvec_y(i,j)<0
theta(i,j) = 3*pi/2;
end
% 勾配エネルギー係数a
a(i,j) = abar * (1 + xi * cos(k*(theta(i,j)-theta_0)));
% 1階微分
dphidx(i,j) = (phi(ip,j)-phi(im,j))/(2*dx);
dphidy(i,j) = (phi(i,jp)-phi(i,jm))/(2*dy);
% 9点ラプラシアン
lap_phi(i,j) = (2 * (phi(ip,j) + phi(im,j) + phi(i,jp) + phi(i,jm)) ...
+ phi(ip,jp) + phi(im,jm) + phi(im,jp) + phi(ip,jm) - 12 * phi(i,j)) / (3 * dx^2);
lap_temp(i,j) = (2 * (T(ip,j) + T(im,j) + T(i,jp) + T(i,jm))...
+ T(ip,jp) + T(im,jm) + T(im,jp) + T(ip,jm) - 12 * T(i,j)) / (3 * dx^2);
end
end
% フェーズフィールド変数、温度場の時間発展ループ
for i = 1 : nx
for j = 1 : ny
% 隣接節点
ip = i + 1;
im = i - 1;
jp = j + 1;
jm = j - 1;
% ノイマン条件
if ip > nx
ip = nx;
end
if im < 1
im = 1;
end
if jp > ny
jp = ny;
end
if jm < 1
jm = 1;
end
% aの微係数計算
A(i, j) = a(i,j)*abar*k*xi*sin(k*(theta(i,j)-theta_0))*dphidy(i,j);
B(i, j) = a(i,j)*abar*k*xi*sin(k*(theta(i,j)-theta_0))*dphidx(i,j);
dadx(i,j) = (a(ip,j)-a(im,j))/(2*dx);
dady(i,j) = (a(i,jp)-a(i,jm))/(2*dy);
% 化学的駆動力の増分の計算
dg(i,j) = latent * (T(i,j)-T_melt)/T_melt;
% フェーズフィールド変数の増分の計算
% エネルギー密度関数１
% dphi(i,j) =...
% -6*dg(i,j)*phi(i,j)*(1-phi(i,j)) - 2*w*phi(i,j)*(1-phi(i,j))*(1-2*phi(i,j))...
% +2*a(i,j,step)*(dadx(i,j)*dphidx(i,j)+dady(i,j)*dphidy(i,j))...
% +a(i,j,step)^(2)*lap_phi(i,j)...
% +(A(ip,j)-A(im,j))/(2*dx)-((B(i,jp)-B(i,jm))/(2*dy));
% エネルギー密度関数２
dphi(i,j) =...
-30*dg(i,j)*phi(i,j)^2*(1-phi(i,j))^2 - 2*w*phi(i,j)*(1-phi(i,j))*(1-2*phi(i,j))...
+2*a(i,j)*(dadx(i,j)*dphidx(i,j)+dady(i,j)*dphidy(i,j))...
+a(i,j)^(2)*lap_phi(i,j)...
+(A(ip,j)-A(im,j))/(2*dx)-((B(i,jp)-B(i,jm))/(2*dy));
% フェーズフィールド変数の時間発展
phi_new(i,j) = phi(i,j) + dt * mp * dphi(i,j);
% 温度場の増分の計算
%q(i,j) = 6*latent*phi(i,j)*(1-phi(i,j))*(phi_new(i,j)-phi(i,j))/dt;
q(i,j) = 30*latent*phi(i,j)^2*(1-phi(i,j))^2*(phi_new(i,j)-phi(i,j))/dt;% 9点ラプラシアン
dT(i,j) = (1 / cv)*(K* lap_temp(i,j) +q(i,j));
% 温度場の時間発展
T_new(i,j) = T(i,j) + dt *dT(i,j);
end
end
% タイムステップを置き換える
phi = phi_new;
T = T_new;
% 動画保存
if step == 1
plotconfig(xl, yl, xmin,xmax, ymin,ymax,step,dt,ax1,ax2,ax3,T_0,T_melt,phi,T,q)
v = VideoWriter(filename,'MPEG-4');
v.FrameRate = 40;
open(v);
elseif mod(step, 60) == 0
plotconfig(xl, yl, xmin,xmax, ymin,ymax,step,dt,ax1,ax2,ax3,T_0,T_melt,phi,T,q)
frame = getframe(gcf);
writeVideo(v,frame);
end
end
% 動画ファイルを閉じる
close(v);
% 以下ローカル関数---------------------------------------------------------------
% 可視化
function [] = plotconfig(xl, yl, xmin,xmax, ymin,ymax,step,dt,ax1,ax2,ax3,T_0,T_melt,phi,T,q)
% Phase-field サブプロット
axes(ax1);
cla(ax1);
imagesc(xl, yl, imrotate(phi(:,:), 90), [0, 1]);
title(ax1, sprintf('phase-field $\\phi$ at %.3e [s]', step*dt), 'Interpreter', 'latex');
cb1 = colorbar(ax1);
title(cb1, '$\phi$', 'Interpreter', 'latex');
axis(ax1, 'equal');
axis(ax1, 'tight');
xlabel('$$x\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
ylabel('$$y\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
xticks(linspace(xmin, xmax, 6)); % x軸の目盛りを設定
yticks(linspace(ymin, ymax, 6)); % y軸の目盛りを設定
ax1.XAxis.TickLabelFormat = '%,.1f';
ax1.YAxis.TickLabelFormat = '%,.1f';
set(ax1, 'YDir', 'normal', 'FontName', 'Times New Roman', 'FontSize', 12,'LineWidth',1.2);
% 温度場 サブプロット
T_min = T_0;
T_max = T_melt;
axes(ax2);
cla(ax2);
imagesc(xl, yl, imrotate(T(:,:), 90), [T_min, T_max]);
title(ax2, sprintf('temperature $T \\rm{[K]}$ at %.3e [s]', step*dt), 'Interpreter', 'latex');
cb2 = colorbar(ax2);
title(cb2, '$T$', 'Interpreter', 'latex');
axis(ax2, 'equal');
axis(ax2, 'tight');
xlabel('$$x\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
ylabel('$$y\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
xticks(linspace(xmin, xmax, 6)); % x軸の目盛りを設定
yticks(linspace(ymin, ymax, 6)); % y軸の目盛りを設定
ax2.XAxis.TickLabelFormat = '%,.1f';
ax2.YAxis.TickLabelFormat = '%,.1f';
set(ax2, 'YDir', 'normal', 'FontName', 'Times New Roman', 'FontSize', 12,'LineWidth',1.2);
% 潜熱コンター
q_min = -3.106811707055531e+17;
q_max = 2.210685380238862e+19;
axes(ax3);
cla(ax3);
imagesc(xl, yl, imrotate(q(:,:), 90), [q_min, q_max]);
title(ax3, sprintf('latent heat $q \\rm{[W/m^3]}$ at %.3e [s]', step*dt), 'Interpreter', 'latex');
cb3 = colorbar(ax3);
title(cb3, '$q$', 'Interpreter', 'latex');
axis(ax3, 'equal');
axis(ax3, 'tight');
xlabel('$$x\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
ylabel('$$y\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
xticks(linspace(xmin, xmax, 6)); % x軸の目盛りを設定
yticks(linspace(ymin, ymax, 6)); % y軸の目盛りを設定
ax3.XAxis.TickLabelFormat = '%,.1f';
ax3.YAxis.TickLabelFormat = '%,.1f';
set(ax3, 'YDir', 'normal', 'FontName', 'Times New Roman', 'FontSize', 12, 'LineWidth', 1.2);
% 新しいプロットの時、軸設定を保持したまま前のグラフィックスオブジェクトを消去
set(gca,'nextplot','replacechildren');
endおわりに
今回は純物質凝固のシミュレーションを行いました。デンドライド構造が予測できたことで、より実際の組織構造の予測に近づいてきた感じがします。同時にその予測にかかるメッシュ数の多さから、フェーズフィールド法の計算コストについても実感し始めました。この辺りは参考文献だとGPUを用いた計算の高速化が図られています。
次回はなぜデンドライトのような不思議な構造が発生するのか、そのメカニズムについてまとめたいと思います。
参考文献
[1] 高木 知弘ら, “フェーズフィールド法”, 養賢堂, 2012/3/2
[2] 山中 晃徳ら, “Pythonによるフェーズフィールド法入門 基礎理論からデータ同化の実装まで”, 丸善出版, 2023/12/15
[3] Wikipedia,Nine-point stencil, https://en.wikipedia.org/wiki/Nine-point_stencil#cite_note-:0-1
コメント