フェーズフィールド法⑭：WBMモデル①

はじめに

　２元系合金の凝固に関する基本的なモデルとしては、1991年頃にWheeler、Boettinger、McFaddenらによって提案されたWBMモデル[4]が知られています。WBMモデルはアレン-カーン方程式とカーン-ヒリアード方程式を連成することで、温度・濃度を駆動力としたデンドライド形成過程を精密にシミュレートすることが出来ます。今回の記事から２回に分けてその詳細をまとめます。本記事ではまずアレン-カーン方程式の導出まで進めたいと思います。

エントロピー増大のアレン-カーン方程式

　WBMモデルにおいて、フェーズフィールド変数の時間発展は以下のエントロピー\(S\)に関するアレン-カーン方程式によって記述されます。

\begin{align}
\frac{d\phi}{dt}=M_{\phi}\frac{\delta S}{\delta \phi}\tag{1}
\end{align}

ここまでの記事ではフェーズフィールド変数を解く際には以下のようなギブスの自由エネルギー\(G\)に関するアレン-カーン方程式を用いてきました。[1]

\begin{align}
\frac{\partial \phi}{\partial t}=-M_{\phi}\frac{\delta G}{\delta \phi} \tag{A1}\\
\end{align}

この式は時間とともにギブスの自由エネルギー\(G\)が減少することを示すものでした。しかし、これがヘルムホルツの自由エネルギー\(F\)の減少や符号を変えてエントロピー\(S\)の増大として表現されても熱力学的には何ら問題ないのでしょう。ようは系の変化の方向を何らかの熱力学変数を用いて表現出来ればいずれの表式でも良いわけです。

この時エントロピー\(S\)はバルクのエントロピーと界面のエントロピーの和として表され、次のように与えられます。

\begin{align}
S=\int s_{dens}dV =\int s(\phi ,e , c)-\frac{\epsilon}{2} \left| \nabla \phi\right|^2dV \tag{2}
\end{align}

最右辺第一項目はバルクのエントロピー密度（熱力学で与えられる一般的なエントロピー）を表します。この項はフェーズフィールド変数\(\phi\)、内部エネルギー\(e\)、金属元素Bの濃度\(c\)の3つの独立変数を用いて表されます。

第二項目は勾配エントロピー密度（勾配補正項）と呼ばれ、界面のエントロピーを表します。\(\epsilon\)は勾配エントロピーの大きさを決める係数（勾配係数）です。界面エネルギーはフェーズフィールド変数の勾配がより小さく（緩やかに）なる方向が安定なので（過去記事参照）、エントロピー増大の法則を踏まえると、符号はマイナスとなることに注意しましょう。

上記のようにフェーズフィールド法では、バルクのエントロピー密度に勾配補正項を加えることで、組織のエントロピー（エネルギー）状態を表現します。

従って、式\((2)\)を用いると汎関数微分の定義よりアレン-カーン方程式\((1)\)は以下のように書けます。

\begin{align}
\frac{d\phi}{dt}&=M_{\phi}\frac{\delta S}{\delta \phi}\\
&=M_{\phi}\left[\frac{\partial s_{dens}}{\partial \phi}
-\nabla \cdot
\left(\frac{\partial s_{dens}}{\partial \left(\nabla \phi\right)}\right)
\right] \\
&=\frac{\partial}{\partial \phi}\left( s(\phi ,e , c)-\frac{\epsilon ^2}{2} \left| \nabla \phi\right|^2\right)-\nabla \cdot\frac{\partial }{\partial \left(\nabla \phi\right)}\left(s(\phi ,e , c)-\frac{\epsilon^2}{2} \left| \nabla \phi\right|^2\right)\\
&=\frac{\partial s(\phi ,e , c)}{\partial \phi} +\nabla \cdot\frac{\partial }{\partial \left(\nabla \phi\right)}\left(\frac{\epsilon^2}{2} \left| \nabla \phi\right|^2\right)\tag{3}
\end{align}

上記は\(\phi\)に関する汎関数微分であり、\(\phi,\nabla \phi\)での微分演算が含まれます。次節より最右辺の各項を計算していきます。

界面のエントロピー項（界面異方性）

　式\((3)\)右辺第一項\(\frac{\partial s(\phi ,e , c)}{\partial \phi} \)の計算は、バルクのエントロピー密度\(s(\phi ,e , c)\)の具体的な形を決めたうえで計算しなくてはいけないので、少々長くなります。そこでまず過去記事にて類似の導出をしたことがある第二項（界面のエントロピー項）\(\nabla \cdot\frac{\partial }{\partial \left(\nabla \phi\right)}\left(\frac{\epsilon^2}{2} \left| \nabla \phi\right|^2\right)\)の計算してしまいましょう。

界面勾配係数\(\epsilon\)は界面異方性を考慮すると、以下のように与えられます。

\begin{align}
\epsilon=\tilde{\epsilon} \eta(k,\theta) =\tilde{\epsilon} \left[1+\gamma \cos\left\{k\left(\theta -\theta _0 \right) \right\} \right] \tag{4}
\end{align}

ここで\(\tilde{\epsilon}\)は基準となる勾配係数、\(\gamma\)は異方性の強さを表す異方性強度、\(k\)は異方性の周期性を表す異方性モード、\(\theta _ 0\)は優先成長方向を表します。

また、簡単のため２次元で考えると、\(\theta\)は\(x\)軸と界面法線ベクトル\(n\)の成す角度を表し、次式で計算されます。

\begin{align}
\theta = \tan^{-1}{\frac{\frac{\partial \phi}{\partial y} }{\frac{\partial \phi}{\partial x} }}
\tag{5}\\
\end{align}

上式より\(\eta\)は\(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y}\)の関数となり、\(\nabla \phi\)による偏微分の影響を受けることに注意しましょう。

したがって、式\((4)\)は以下のように変形できます。

\begin{align}
\nabla \cdot\frac{\partial }{\partial \left(\nabla \phi\right)}\left(\frac{\epsilon^2}{2} \left| \nabla \phi\right|^2\right)&=
\frac{\tilde{\epsilon} ^2}{2} \nabla \cdot\frac{\partial }{\partial \left(\nabla \phi\right)}\left(\eta ^2 \left| \nabla \phi\right|^2\right)\\

&=
\frac{\tilde{\epsilon} ^2}{2}
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\frac{\partial }{\partial \left(\frac{\partial \phi }{\partial x} \right)} \\ \frac{\partial \phi }{\partial \left(\frac{\partial \phi }{\partial y} \right)}
\end{pmatrix}
\eta ^2\left[\left( \frac{\partial \phi}{\partial x}\right)^2+\left(\frac{\partial \phi}{\partial y}\right)^2\right]\\

&=
\frac{\tilde{\epsilon} ^2}{2}
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\frac{\partial \eta^2 }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left[\left( \frac{\partial \phi}{\partial x}\right)^2+\left(\frac{\partial \phi}{\partial y}\right)^2\right]+2\eta^2 \frac{\partial \phi }{\partial x}
\\
\frac{\partial \eta^2 }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left[\left( \frac{\partial \phi}{\partial x}\right)^2+\left(\frac{\partial \phi}{\partial y}\right)^2\right]+2\eta^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}
\\
&=

\frac{\tilde{\epsilon} ^2}{2}
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\frac{\partial \eta^2 }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left(\nabla \phi\right)^2+2\eta^2 \frac{\partial \phi }{\partial x}
\\
\frac{\partial \eta^2 }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left(\nabla \phi\right)^2+2\eta^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}
\\

&=
\frac{\tilde{\epsilon} ^2}{2}

\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\frac{\partial \eta^2 }{\partial \eta } \frac{\partial \eta }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left(\nabla \phi\right)^2+2\eta^2 \frac{\partial \phi }{\partial x}
\\
\frac{\partial \eta^2 }{\partial \eta } \frac{\partial \eta }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left(\nabla \phi\right)^2+2\eta^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}
\\
&=
\tilde{\epsilon} ^2

\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\eta \frac{\partial \eta }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left(\nabla \phi\right)^2+\eta^2 \frac{\partial \phi }{\partial x}
\\
\eta\frac{\partial \eta }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left(\nabla \phi\right)^2+\eta^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}
\tag{6}
\end{align}

ここで\(\theta\)の偏微分項には次の関係式が成り立ちます。

\begin{align}
\frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial x}\right) }&=-\frac{\frac{\partial \phi }{\partial y}}{\left(\nabla \phi\right)^2 }
\tag{7}\\
\frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial y}\right) }&=\frac{\frac{\partial \phi }{\partial x}}{\left(\nabla \phi\right)^2 }
\tag{8}
\end{align}

式\((7),(8)\)の導出

\begin{align}
\frac{\partial \left(\frac{\partial \phi }{\partial x}\right) }{\partial \theta }
&=\frac{\partial }{\partial \theta }\left( \frac{\frac{\partial \phi }{\partial y}}{\tan \theta}\right)\\
&=\frac{\partial \phi }{\partial y}\left( \frac{-\frac{1}{\cos^2 \theta}}{\tan^2 \theta}\right)\\
&=-\frac{\frac{\partial \phi }{\partial y}}{\sin^2 \theta}\\
&=-\frac{\frac{\partial \phi }{\partial y}}{\left(\frac{\frac{\partial \phi}{\partial y}}{\left[\left(\frac{\partial \phi }{\partial x}\right)^2+\left(\frac{\partial \phi }{\partial y}\right)^2\right]^\frac{1}{2}}\right)^2}\\
&=-\frac{\left(\nabla \phi\right)^2 }{\frac{\partial \phi }{\partial y}}\\
\rightarrow
\frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial x}\right) }&=-\frac{\frac{\partial \phi }{\partial y}}{\left(\nabla \phi\right)^2 }
\tag{B1}\\
\end{align}

同様に、

\begin{align}
\frac{\partial \left(\frac{\partial \phi }{\partial y}\right) }{\partial \theta }
&=\frac{\partial }{\partial \theta }\left(\frac{\partial \phi }{\partial x}\tan \theta\right)\\
&=\frac{\frac{\partial \phi }{\partial x}}{\cos^2 \theta}\\
&=\frac{\frac{\partial \phi }{\partial x}}{\left(\frac{\frac{\partial \phi}{\partial x}}{\left[\left(\frac{\partial \phi }{\partial x}\right)^2+\left(\frac{\partial \phi }{\partial y}\right)^2\right]^\frac{1}{2}}\right)^2}\\
&=\frac{\left(\nabla \phi\right)^2 }{\frac{\partial \phi }{\partial x}}\\
\rightarrow
\frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial y}\right) }&=\frac{\frac{\partial \phi }{\partial x}}{\left(\nabla \phi\right)^2 }
\tag{B2}\\
\end{align}

これらを式\((6)\)に代入すると、

\begin{align}
\nabla \cdot\frac{\partial }{\partial \left(\nabla \phi\right)}\left(\frac{\epsilon^2}{2} \left| \nabla \phi\right|^2\right)&=
\tilde{\epsilon} ^2
\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
\eta \frac{\partial \eta }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial x}\right) } \left(\nabla \phi\right)^2+\eta^2 \frac{\partial \phi }{\partial x}
\\
\eta\frac{\partial \eta }{\partial \theta } \frac{\partial \theta }{\partial \left(\frac{\partial \phi }{\partial y}\right) } \left(\nabla \phi\right)^2+\eta^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}\\
&=
\tilde{\epsilon} ^2

\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
-\eta \frac{\partial \eta }{\partial \theta }\frac{\frac{\partial \phi }{\partial y}}{\left(\nabla \phi\right)^2 } \left(\nabla \phi\right)^2+\eta^2 \frac{\partial \phi }{\partial x}
\\
\eta\frac{\partial \eta }{\partial \theta } \frac{\frac{\partial \phi }{\partial x}}{\left(\nabla \phi\right)^2 }\left(\nabla \phi\right)^2+\eta^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}\\
&=
\tilde{\epsilon} ^2

\begin{pmatrix}
\frac{\partial }{\partial x} \\ \frac{\partial }{\partial y}
\end{pmatrix}
\cdot
\begin{pmatrix}
-\eta \frac{\partial \eta }{\partial \theta }\frac{\partial \phi }{\partial y} +\eta^2 \frac{\partial \phi }{\partial x}
\\
\eta\frac{\partial \eta}{\partial \theta } \frac{\partial \phi }{\partial x}+\eta^2 \frac{\partial \phi }{\partial y}
\end{pmatrix}\\
&=
\tilde{\epsilon} ^2
\left[
\frac{\partial }{\partial x}
\left(
-\eta \frac{\partial \eta }{\partial \theta }\frac{\partial \phi }{\partial y} +\eta^2 \frac{\partial \phi }{\partial x}
\right)
+
\frac{\partial }{\partial y}
\left(
\eta\frac{\partial \eta }{\partial \theta } \frac{\partial \phi }{\partial x}+\eta^2 \frac{\partial \phi }{\partial y}
\right)
\right]
\\
&=
\tilde{\epsilon} ^2
\left[
\frac{\partial }{\partial x} \left(\eta^2 \frac{\partial \phi }{\partial x}\right)
+\frac{\partial }{\partial y} \left(\eta^2 \frac{\partial \phi }{\partial y}\right)
– \frac{\partial }{\partial x}\left(\eta\frac{\partial \eta }{\partial \theta }\frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
\eta\frac{\partial \eta }{\partial \theta } \frac{\partial \phi }{\partial x}
\right)
\right]\\
&=
\tilde{\epsilon} ^2
\left[
\nabla \cdot \left(\eta^2 \nabla \phi \right)
– \frac{\partial }{\partial x}\left(\eta\frac{\partial \eta }{\partial \theta }\frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
\eta\frac{\partial \eta }{\partial \theta } \frac{\partial \phi }{\partial x}
\right)
\right] \tag{9}
\end{align}

以上で界面のエントロピー項（式\((3)\)右辺第二項）を求めることが出来ました。

バルクのエントロピー項

　次に式\((3)\)右辺第一項（バルクのエントロピー項）\(\frac{\partial s(\phi ,e , c)}{\partial \phi}\)を計算するために、まずエントロピー密度\( s(\phi ,e , c)\)の具体的な表式から決めていきます。

ヘルムホルツの自由エネルギー密度\(f\rm{[J/m^3]}\)とエントロピー密度\( s(\phi ,e , c)\rm{[J/(K\cdot m^3)]}\)の間には次のような熱力学的な関係式が成り立ちます。

\begin{align}
f=e-Ts\rightarrow s=\frac{1}{T}\left(e-f\right)\tag{10}
\end{align}

ここで\(e\)は内部エネルギー密度\(\rm{[J/m^3]}\)です。上式から\(f,e\)が分かれば\(s\)も分かるというわけです。

内部エネルギー密度

　まず内部エネルギー密度\(e\)を求めます。今回は二元系なのでA、Bの二種の金属元素が存在しますが、ここでは元素Aを例に考えます。

純粋な元素Aの固相・液相でのエネルギーを\(e_{S}^{A},e_{L}^{A}\)を用いると、内部エネルギー\(e^{A}\)は次のように表わされます。

\begin{align}
e^{A}=e_{S}^{A}+p(\phi)\left(e_{L}^{A}-e_{S}^{A}\right)\tag{11}
\end{align}

ここで\(p(\phi)\)は、固相（\(\phi=0\)）のとき\(p(\phi)=0\)、液相（\(\phi=1\)）のとき\(p(\phi)=1\)となり、その間を滑らかにつなぐ関数とします。液相と固相の比率に応じて、各相のエネルギー密度を重みづけるイメージです。ただし現段階では\(p(\phi)\)の具体的な形は決めないでおきます。

また、\(e_{S}^{A},e_{L}^{A}\)は元素Aの純粋な融点\(T_{m}^{A}\)を基準に考えると以下のように書けます。

\begin{align}
元素Aが固体（T< T_{m}^{A})のとき　e_{S}^{A}(T)=e_{S}^{A}(T_{m}^{A})+C_{S}^{A}(T-T_{m}^{A})\tag{12}\\
元素Aが液体（T> T_{m}^{A})のとき　e_{L}^{A}(T)=e_{L}^{A}(T_{m}^{A})+C_{L}^{A}(T-T_{m}^{A})\tag{13}\\
\end{align}

ここで\(C_{S}^{A},C_{L}^{A}\)は純粋な元素Aの固体・液体状態における熱容量密度\(\rm{[J/K\cdot m^3]}\)を表します。

以上、式\((12),(13)\)を\((11)\)に代入すると

\begin{align}
e^{A}=e_{S}^{A}(T_{m}^{A})+C_{S}^{A}(T-T_{m}^{A})+p(\phi)\left[e_{L}^{A}(T_{m}^{A})+C_{L}^{A}(T-T_{m}^{A})-e_{S}^{A}(T_{m}^{A})-C_{S}^{A}(T-T_{m}^{A})\right]\tag{14}
\end{align}

となります。また実際の計算の時には、簡単のため固相と液相の比熱は等しいと仮定します。

\begin{align}
C_{S}^{A}=C_{L}^{A}=C^{A}\tag{15}\\
\end{align}

これにより、式\((14)\)の右辺第三項の熱容量の項は打ち消しあい、次式が得られます。

\begin{align}
e^{A}=e_{S}^{A}(T_{m}^{A})+C^{A}(T-T_{m}^{A})+p(\phi)\left[e_{L}^{A}(T_{m}^{A})-e_{S}^{A}(T_{m}^{A})\right]\tag{16}
\end{align}

さらに、\(e_{S}^{A}(T_{m}^{A}),e_{L}^{A}(T_{m}^{A})\)は潜熱\(L^{A}\)の分だけ異なるとし、次のように表します。

\begin{align}
L^{A}=e_{L}^{A}(T_{m}^{A})-e_{S}^{A}(T_{m}^{A})\tag{17}\\
\end{align}

式\((17)\)を式\((16)\)に代入すると、最終的に内部エネルギー密度は以下のように書けます。

\begin{align}
e^{A}=e_{S}^{A}(T_{m}^{A})+C^{A}(T-T_{m}^{A})+p(\phi)L^{A}\tag{18}
\end{align}

上式をグラフにすると、次のようなイメージです。

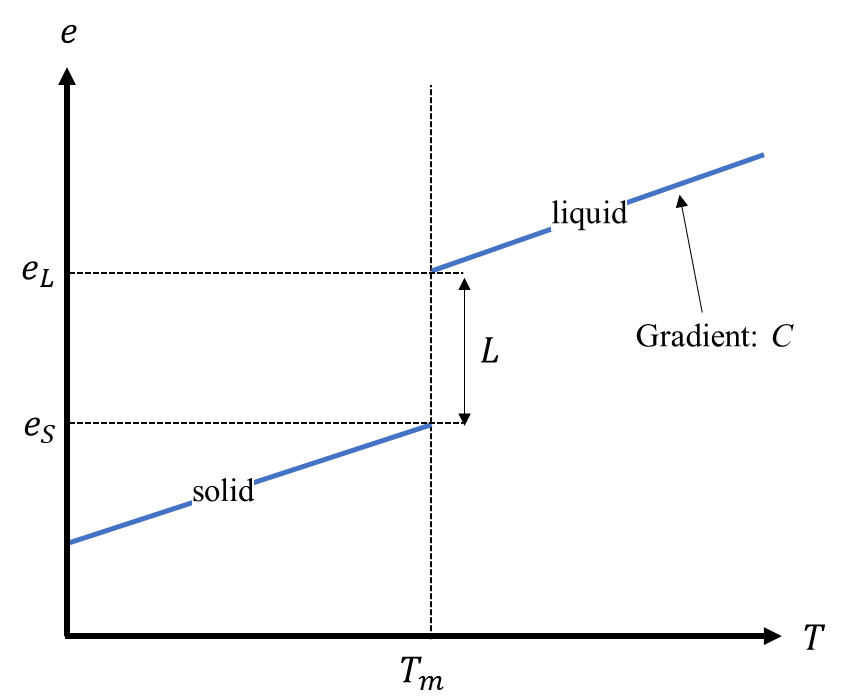
ヘルムホルツの自由エネルギー密度

　次はヘルムホルツの自由エネルギー密度\(f\)について考えます。式\((10)\)の全微分を考えると、

\begin{align}
df=de-Tds-sdT\tag{19}
\end{align}

より、

\begin{align}
s=-\frac{\partial f}{\partial T}\tag{20}
\end{align}

となるので、これをもとの式\((10)\)に代入すると次式が得られます。

\begin{align}
f=e+T\frac{\partial f}{\partial T}\tag{21}
\end{align}

純粋な元素Aの自由エネルギーのみを考える場合、以下のように書いてよいでしょう。

\begin{align}
f_{A}=e_{A}+T\frac{\partial f_{A}}{\partial T}\tag{22}
\end{align}

上式に式\((18)\)を代入すると以下の\(f_{A}(T,\phi)\)に関する偏微分方程式が得られます。

\begin{align}
f_{A}=e_{S}^{A}(T_{m}^{A})+C^{A}(T-T_{m}^{A})+p(\phi)L^{A}+T\frac{\partial f_{A}}{\partial T}\tag{23}
\end{align}

天下りではありますが、上式の解は以下のように書くことが出来ます。

\begin{align}
f_{A}=G^{A}(\phi)T+\left[e_{S}^{A}(T_{m}^{A})-C^{A}T_{m}^{A}+p(\phi)L^{A}\right] \left(1-\frac{T}{T_{m}^{A}}\right)-C^{A}T\log {\frac{T}{T_{m}^{A}}}\tag{24}
\end{align}

式\((23)\)は\(f_{A}(T,\phi)\)の温度\(T\)に関する偏微分方程式なので、\(\phi\)に関する任意関数\(G^{A}(\phi)\)が付くことに注意しましょう。唐突に解を記載してしまいましたが、実際に式\((24)\)を式\((23)\)に代入すると確かに解になってることが分かります。

次に物理的考察に基づいて、\(G^{A}(\phi),p(\phi)\)の形を決めていきます。

文献[2]において、ヘルムホルツの自由エネルギー\(f\)は下記条件を満たすとしています。

固液相変化（\(T=T_{m}\)）において、自由エネルギー\(f(T,\phi)\)は連続的に変化する。
\begin{align}
f(T_{m},0)=f(T_{m},1)\tag{25}
\end{align}
いかなる温度\(T\)に対しても、固相状態（\(\phi = 0\)）と液相状態（\(\phi = 1\)）において極小値を持つ。（＝純物質の場合、固相または液相状態がエネルギー的に安定であり、それらが混合した状態にはならない。）
\begin{align}
\left(\frac{\partial f}{\partial \phi}\right)_{\phi=0,1}=0\tag{26}\\
\left(\frac{\partial ^2 f}{\partial \phi ^2}\right)_{\phi=0,1}>0\tag{27}\\
\end{align}

これらの条件の妥当性については議論の余地がある気もしますが、ひとまず受け入れて計算を進めましょう。

式\((25)\)を式\((24)\)に代入すると、次のようになります。

\begin{align}
G^{A}(0)T_{m}^{A}&+\left[e_{S}^{A}(T_{m}^{A})-C^{A}T_{m}^{A}+p(0)L^{A}\right] \left(1-\frac{T_{m}^{A}}{T_{m}^{A}}\right)-C^{A}T_{m}^{A}\log {\frac{T_{m}^{A}}{T_{m}^{A}}}\\
&=G^{A}(1)T_{m}^{A}+\left[e_{S}^{A}(T_{m}^{A})-C^{A}T_{m}^{A}+p(1)L^{A}\right] \left(1-\frac{T_{m}^{A}}{T_{m}^{A}}\right)-C^{A}T_{m}^{A}\log {\frac{T_{m}^{A}}{T_{m}^{A}}}\\
&\quad\quad\quad\quad\quad\quad\quad\quad\quad\rightarrow G^{A}(0)=G^{A}(1)\tag{28}
\end{align}

また、

\begin{align}
\frac{\partial f_{A}}{\partial \phi}&=\frac{\partial }{\partial \phi}\left\{G^{A}(\phi)T+\left[e_{S}^{A}(T_{m}^{A})-C^{A}T_{m}^{A}+p(\phi)L^{A}\right] \left(1-\frac{T}{T_{m}^{A}}\right)-C^{A}T\log {\frac{T}{T_{m}^{A}}}\right\}\\
&=T\frac{\partial G^{A}( \phi)}{\partial \phi}+L^{A}\left(1-\frac{T}{T_{m}^{A}}\right)\frac{\partial p(\phi)}{\partial \phi} \tag{29}\\
\frac{\partial ^2 f_{A}}{\partial \phi^2}&=T\frac{\partial^2 G^{A}( \phi)}{\partial \phi^2}+L^{A}\left(1-\frac{T}{T_{m}^{A}}\right)\frac{\partial^2 p(\phi)}{\partial \phi^2} \tag{30}\\
\end{align}

より、式\((26),(27)\)は次のように書くことも出来ます。

\begin{align}
&\left[\frac{\partial G^{A}( \phi)}{\partial \phi}+\frac{L^{A}}{T}\left(1-\frac{T}{T_{m}^{A}}\right)\frac{\partial p(\phi)}{\partial \phi} \right]_{\phi=0,1}=0\tag{31}\\
&\left[\frac{\partial^2 G^{A}( \phi)}{\partial \phi^2}+\frac{L^{A}}{T}\left(1-\frac{T}{T_{m}^{A}}\right)\frac{\partial^2 p(\phi)}{\partial \phi^2} \right]_{\phi=0,1}>0\tag{32}\\
\end{align}

さて、以上の条件を満たす、\(G^{A}(\phi),p(\phi)\)はどのような形が適切でしょうか？

まずは\(G^{A}(\phi)\)について考えます。文献[4]においては\(G^{A}(\phi)\)は次のように与えられます。

\begin{align}
G^{A}( \phi)&=W^{A}g(\phi)=W^{A}\phi ^2\left(\phi -1\right)^2\tag{33}\\
\end{align}

上式は\(G^{A}(0)=G^{A}(1)=0\)となり、式\((28)\)の条件を満たしていることが分かります。

また上式を用いると、式\((31),(32)\)は次のように変形できます。

\begin{align}
&\left[\frac{\partial g( \phi)}{\partial \phi}+\frac{L^{A}}{W_{A}T}\left(1-\frac{T}{T_{m}^{A}}\right)\frac{\partial p(\phi)}{\partial \phi} \right]_{\phi=0,1}=0\tag{34}\\
&\left[\frac{\partial^2 g( \phi)}{\partial \phi^2}+\frac{L^{A}}{W_{A}T}\left(1-\frac{T}{T_{m}^{A}}\right)\frac{\partial^2 p(\phi)}{\partial \phi^2} \right]_{ \phi=0,1}>0\tag{35}\\
\end{align}

ここで\(g( \phi)\)の微分係数は以下のように計算できます。

\begin{align}
\frac{\partial g( \phi)}{\partial \phi}&=2\phi \left(\phi -1\right)^2+2\phi^2\left(\phi -1\right)\\
&=2\phi\left(\phi -1\right)\left[ \left(\phi -1\right)+\phi\right]\\
&=2\phi\left(\phi -1\right) \left(2\phi -1\right)\tag{36}\\
\frac{\partial^2 g( \phi)}{\partial \phi^2}
&=2\left(\phi -1\right) \left(2\phi -1\right)+2\phi\left(2\phi -1\right)+4\phi\left(\phi -1\right) \\
&= 2\left(2\phi -1\right)^2+4\phi\left(\phi -1\right)
\tag{37}\\
\end{align}

従って、\(\phi=0,1\)の時の導関数は次の通りです。

\begin{align}
\left(\frac{\partial g( \phi)}{\partial \phi}\right)_{\phi=0}&=\left(\frac{\partial g( \phi)}{\partial \phi}\right)_{\phi=1}=0
\tag{38}\\
\left(\frac{\partial^2 g( \phi)}{\partial \phi^2}\right)_{\phi=0}&=\left(\frac{\partial^2 g( \phi)}{\partial \phi^2}\right)_{\phi=1}=1
\tag{39}\\
\end{align}

つまり一階微分すると、領域の両端（\(\phi=0,1\)）で０、二階微分すると１となるわけです。中々分かりやすい性質をしています。ただ、これだけでは、式\((34),(35)\)の条件を満たすのかは分かりません。\(p(\phi)\)の形が未知だからです。

\(p(\phi)\)は式\((11)\)にて固相・液相の内部エネルギー密度を表すために導入されており、\(p(0)=0,p(1)=1\)であるとだけ決めていました。

\(p(\phi)\)は文献[4]においては次式で与えるとされています。

\begin{align}
p(\phi)&=\frac{\int_{0}^{\phi} g(\zeta)d \zeta}{\int_{0}^{1} g(\zeta)d \zeta}=\frac{\int_{0}^{\phi}\zeta ^2\left(\zeta -1\right)^2d \zeta}{\int_{0}^{1} \zeta ^2\left(\zeta -1\right)^2d \zeta}\\
&=\frac{\int_{0}^{\phi}\zeta^4 -2\zeta^3+\zeta^2 d \zeta}{\int_{0}^{1} \zeta^4 -2\zeta^3+\zeta^2 d \zeta}\\
&=\frac{[\frac{1}{5}\zeta ^5 -\frac{2}{4}\zeta^4+\frac{1}{3}\zeta^3]_{0}^{\phi}}{[\frac{1}{5}\zeta ^5 -\frac{2}{4}\zeta^4+\frac{1}{3}\zeta^3]_{0}^{1}}\\
&=\frac{\frac{1}{5}\phi ^5 -\frac{1}{2}\phi^4+\frac{1}{3}\phi^3}{\frac{1}{5} -\frac{1}{2}+\frac{1}{3}}\\
&=\frac{6\phi ^5 -15\phi^4+10\phi^3}{6 -15+10}\\
&=\phi^3\left(6\phi ^2 -15\phi+10\right)
\tag{40}
\end{align}

\(\zeta\)はフェーズフィールド変数で、積分して\(\phi\)を代入する関係上用いています。

上式分母は規格化を表しており、\(p(0)=0,p(1)=1\)となるようにするための操作です。また分子は\(g(\phi)\)の積分値となっており、これは\(p(\phi)\)が\(g(\phi)\)より微分階数が一階低いことを示しています。要は次のように\(p(\phi)\)を\(\phi\)で微分すると\(g(\phi)\)が現れるわけです。

\begin{align}
\frac{\partial p( \phi)}{\partial \phi}&=\frac{\partial}{\partial \phi}\left[\phi^3\left(6\phi ^2 -15\phi+10\right)\right]\\
&=30\phi ^4 -60\phi^3+30\phi^2\\
&=30\phi ^2\left(\phi ^2 -2\phi+1\right)\\
&=30\phi ^2\left(\phi -1\right)^2\\
&=30g(\phi)\tag{41}\\
\frac{\partial^2 p( \phi)}{\partial \phi^2}\
&=30\frac{\partial g( \phi)}{\partial \phi}\\
&=30\phi\left(\phi -1\right) \left(2\phi -1\right)\tag{42}\\
\end{align}

従って、\(\phi=0,1\)の時の微分係数は次の通りです。

\begin{align}
\left(\frac{\partial p( \phi)}{\partial \phi}\right)_{\phi=0}&=\left(\frac{\partial p( \phi)}{\partial \phi}\right)_{\phi=1}=0\tag{43}\\
\left(\frac{\partial^2 p( \phi)}{\partial \phi^2}\right)_{\phi=0}&=\left(\frac{\partial^2 p( \phi)}{\partial \phi^2}\right)_{\phi=1}=0\tag{44}\\
\end{align}

つまり、微係数は計算領域両端で常に０になります。

このように\(p(\phi)\)を設定すると、式\((34),(35)\)の左辺第二項は常に0となり、式\((38),(39)\)も踏まえれば、式\((34),(35)\)はいかなる温度においても成立することとなります。

以上をまとめると純粋な元素Aのヘルムホルツの自由エネルギーは以下のように与えられます。

\begin{align}
f_{A}&=G^{A}(\phi)T+\left[e_{S}^{A}(T_{m}^{A})-C^{A}T_{m}^{A}+p(\phi)L^{A}\right] \left(1-\frac{T}{T_{m}^{A}}\right)-C^{A}T\log {\frac{T}{T_{m}^{A}}}\tag{45}\\
G^{A}( \phi)&=W^{A}g(\phi)=W^{A}\phi ^2\left(\phi -1\right)^2\tag{46}\\
p(\phi)&=\phi^3\left(6\phi ^2 -15\phi+10\right)\tag{47}
\end{align}

元素Bの自由エネルギー\(f_{B}\)も同様の形で書くことが出来ます。

ここで定めた\(G(\phi),p(\phi)\)は、物理的考察から導かれた定式化で、一意的に決まるものではありません。「このように設定しておくとうまくいきそうだよ」という感じです。実際、文献[5]では、\(p(\phi)\)に関して\(p(\phi)=\phi^2(3-2\phi)\)と置く場合についても検討がなされています。

また、ここまでは元素Aの自由エネルギー\(f_{A}\)のみ考えてきましたが、全自由エネルギー\(f\)は正則溶体近似を用いると次のように書けます。

\begin{align}
f&=(1-c)\mu_{A}+c\mu_{B}\\
&=(1-c)\left\{f_A(T,\phi)+\Omega(\phi) c^2+\frac{RT}{v_{m}}\log (1-c)\right\}+c\left\{f_B(T,\phi)+\Omega(\phi) (1-c)^2+\frac{RT}{v_{m}}\log c\right\}
\tag{48}
\end{align}

ここで、\(\Omega\)は混合エンタルピー、\(v_{m}\)はモル体積を表します。

式\((48)\)の導出

　系のヘルムホルツの自由エネルギー密度\(f\)は正則溶体近似より次のように書けます。（過去記事参照）

\begin{align}
f&=f_{A}(1-c)+f_{B}c+\Omega(1-c)c+\frac{RT}{v_{m}}\left \{ (1-c) \log (1-c) +c \log c \right \} \tag{C1}
\end{align}

またA-B系溶体の化学ポテンシャル\(\mu_{A},\mu_{B}\)と自由エネルギー密度\(f\)の関係は次式で与えられます。（過去記事参照）

\begin{align}
\mu _{A}&=f-\left(\frac{\partial f}{\partial c }\right)c\tag{C2}\\
\mu _{B}&=f+\left(\frac{\partial f}{\partial c }\right)\left(1-c\right)\tag{C3}\\
\end{align}

ここで式\((C1)\)より自由エネルギー密度\(f\)を濃度\(c\)の偏微分は次のように計算できます。

\begin{align}
\frac{\partial f}{\partial c }&=\frac{\partial }{\partial c }\left(f_{A}(1-c)+f_{B}c+\Omega(1-c)c+\frac{RT}{v_{m}}\left \{ (1-c) \log (1-c) +c \log c \right \}\right)\\
&=-f_{A}+f_{B}+\Omega(1-2c)+\frac{RT}{v_{m}}\left \{ -\log (1-c) -\frac{1-c}{1-c}+\log c +\frac{c}{c}\right \}\\
&=-f_{A}+f_{B}+\Omega(1-2c)+\frac{RT}{v_{m}}\left \{ -\log (1-c) +\log c \right \}\tag{C4}\\
\end{align}

したがって、式\((C4)\)に式\((C2),(C3)\)を代入すると、

\begin{align}
\mu _{A}&=f_{A}(1-c)+f_{B}c+\Omega(1-c)c+\frac{RT}{v_{m}}\left \{ (1-c) \log (1-c) +c \log c \right \}\\
&\quad\quad-\left[-f_{A}+f_{B}+\Omega(1-2c)+\frac{RT}{v_{m}}\left \{ -\log (1-c) +\log c \right \}\right]c\\
&=f_{A}+\Omega c^2+\frac{RT}{v_{m}} \log (1-c) \tag{C5}\\
\mu _{B}&=f_{A}(1-c)+f_{B}c+\Omega(1-c)c+\frac{RT}{v_{m}}\left \{ (1-c) \log (1-c) +c \log c \right \}\\
&\quad\quad+\left[-f_{A}+f_{B}+\Omega(1-2c)+\frac{RT}{v_{m}}\left \{ -\log (1-c) +\log c \right \}\right]\left(1-c\right)\\
&=f_{B}+\Omega \left(1-c\right)^2+\frac{RT}{v_{m}} \log c \tag{C6}\\
\end{align}

化学ポテンシャルは１モル当たりの自由エネルギーと考えられるので、式\((C5),(C6)\)を用いると系の全自由エネルギー密度\(f\)は次のように表されます。

以上で式\((48)\)を求めることが出来ました。

以上がヘルムホルツの自由エネルギー密度の導出です。

バルクのエントロピー項

　最後にエントロピー密度\( s(\phi ,e , c)\)を求めます。式\((10)\)に式\((48)\)を代入すると

\begin{align}
s&=\frac{1}{T}\left(e-f\right)\\
&=\frac{1}{T}\left[e-(1-c)\left\{f_A(T,\phi)+\Omega(\phi) c^2+\frac{RT}{v_{m}}\log (1-c)\right\}\right.\\
&\left.\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad-c\left\{f_B(T,\phi)+\Omega(\phi) (1-c)^2+\frac{RT}{v_{m}}\log c\right\}\right]\tag{49}
\end{align}

したがって、式\((3)\)右辺第一項（バルクのエントロピー項）\(\frac{\partial s(\phi ,e , c)}{\partial \phi}\)は次のように書けます。

\begin{align}
\frac{\partial s(\phi ,e , c)}{\partial \phi}&=\frac{1}{T}\frac{\partial}{\partial \phi}\left[e-(1-c)\left\{f_A(T,\phi)+\Omega(\phi) c^2+\frac{RT}{v_{m}}\log (1-c)\right\}\right.\\
&\left.\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad-c\left\{f_B(T,\phi)+\Omega(\phi) (1-c)^2+\frac{RT}{v_{m}}\log c\right\}\right]\tag{50}
\end{align}

上式はこのまま計算を進めるには複雑なので、以下二つの仮定を課して簡略化することとします。

理想溶体近似を適用し、\(\Omega=0\)とします。これにより、状態図は単純なレンズ型（全率可溶型）に限定されます。しかしながら液体と固体の間の濃度の「ギャップ」という本質的な特徴は維持されます。
温度\(T\)、および内部エネルギー\(e\)は一定とし、エネルギー保存式（非定常熱伝導方程式）は解かないことにします。この仮定は潜熱による温度勾配に起因した界面駆動力よりも溶質の除去（溶液中に溶けている物質が固相に取り込まれず、界面近傍の液相側で濃縮される現象）による界面駆動力の影響が十分に大きい時に成立します。

以上の仮定より、式\((50)\)は以下のように書けます。

\begin{align}
\frac{\partial s}{\partial \phi}&=\frac{1}{T}\frac{\partial}{\partial \phi}\left[e-(1-c)\left\{f_A(T,\phi)+\frac{RT}{v_{m}}\log (1-c)\right\}-c\left\{f_B(T,\phi)+\frac{RT}{v_{m}}\log c\right\}\right]\\
&=\frac{1}{T}\left[-(1-c)\left(\frac{\partial f_A(T,\phi)}{\partial \phi}\right)-c\left(\frac{\partial f_B(T,\phi)}{\partial \phi}\right)\right]
\tag{51}
\end{align}

したがって、式\((46) \sim (48)\)を用いると、

\begin{align}
\frac{\partial s}{\partial \phi}&=\frac{1}{T}\left[-(1-c)\left(\frac{\partial f_A}{\partial \phi}\right)-c\left(\frac{\partial f_B}{\partial \phi}\right)\right]\\
&=-(1-c)\left(\frac{1}{T}\frac{\partial f_A}{\partial \phi}\right)-c\left(\frac{1}{T}\frac{\partial f_B}{\partial \phi}\right)\\
&=-(1-c)\left\{\frac{1}{T}\frac{\partial }{\partial \phi}\left(G^{A}(\phi)T+\left[e_{S}^{A}(T_{m}^{A})-C^{A}T_{m}^{A}+p(\phi)L^{A}\right] \left(1-\frac{T}{T_{m}^{A}}\right)-C^{A}T\log {\frac{T}{T_{m}^{A}}}\right)\right\}\\
&\quad\quad-c\left\{\frac{1}{T}\frac{\partial }{\partial \phi}\left(G^{B}(\phi)T+\left[e_{S}^{B}(T_{m}^{B})-C^{B}T_{m}^{B}+p(\phi)L^{B}\right] \left(1-\frac{T}{T_{m}^{B}}\right)-C^{B}T\log {\frac{T}{T_{m}^{B}}}\right)\right\}\\
&=-(1-c)\left\{\frac{1}{T}\frac{\partial }{\partial \phi}\left(G^{A}(\phi)T+p(\phi)L^{A} \left(1-\frac{T}{T_{m}^{A}}\right)\right)\right\}\\
&\quad\quad\quad\quad\quad\quad\quad\quad-c\left\{\frac{1}{T}\frac{\partial }{\partial \phi}\left(G^{B}(\phi)T+p(\phi)L^{B} \left(1-\frac{T}{T_{m}^{B}}\right)\right)\right\}\\
&=-(1-c)\left\{W^{A}\frac{\partial g}{\partial \phi}+30gL^{A} \left(\frac{1}{T}-\frac{1}{T_{m}^{A}}\right)\right\}-c\left\{W^{B}\frac{\partial g}{\partial \phi}+30gL^{B} \left(\frac{1}{T}-\frac{1}{T_{m}^{B}}\right)\right\}\\
&=-(1-c)H^{A}(T,\phi)-cH^{B}(T,\phi)
\tag{52}
\end{align}

ここで\(H^{A},H^{B}\)は以下のように定義しました。

\begin{align}
H^{A}&=\frac{1}{T}\frac{\partial f_A}{\partial \phi}=W^{A}\frac{\partial g}{\partial \phi}+30gL^{A} \left(\frac{1}{T}-\frac{1}{T_{m}^{A}}\right)\tag{53}\\
H^{B}&=\frac{1}{T}\frac{\partial f_B}{\partial \phi}=W^{B}\frac{\partial g}{\partial \phi}+30gL^{B} \left(\frac{1}{T}-\frac{1}{T_{m}^{B}}\right)\tag{54}
\end{align}

以上でバルクのエントロピー項（式\((3)\)右辺第一項）を求めることが出来ました。

２元系合金の凝固のアレン-カーン方程式

　長くなりましたが、以上で準備が整いました。式\((9),(52)\)を式\((3)\)に代入すると以下の最終的なアレンカーン方程式が得られます。

\begin{align}
\frac{d\phi}{dt}&=
M_{\phi}
\left[
-(1-c)H^{A}(T,\phi)-cH^{B}(T,\phi)\right.\\
&\left.\quad\quad +\tilde{\epsilon} ^2
\left\{
\nabla \cdot \left(\eta^2 \nabla \phi \right)
– \frac{\partial }{\partial x}\left(\eta\frac{\partial \eta }{\partial \theta }\frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
\eta\frac{\partial \eta }{\partial \theta } \frac{\partial \phi }{\partial x}
\right)
\right\}

\right]
\tag{55}
\end{align}

右辺第一、二項の\(H^{A},H^{B}\)は単一元素のバルクのエントロピー増大に由来する駆動力を意味しており、各元素の濃度で重みづけして足し合わせることで、系全体の駆動力を表しています。第三項は界面のエントロピーの増大に由来する駆動力（界面異方性）です。

またこの時、フェーズフィールドモビリティ\(M_{\phi}\)は以下のように純粋な元素の重ね合わせとして表されます。

\begin{align}
M_{\phi}=\left(1-c\right) M^{A}+c M^{B}\tag{56}
\end{align}

以上を解くことで、フェーズフィールド変数の時間発展を得ることが出来ます。

物性値との関連付け

　最後に方程式上の係数(勾配係数\(\epsilon\)、ダブルウェルポテンシャル\(W\)、フェーズフィールドモビリティ\(M_{\phi}\)）と物性値(界面エネルギー\(\gamma\)、界面モビリティ\(M\)、界面幅\(\delta\))の関連付けを行います。ただし今回は二元系なので、二種の元素それぞれについての関係付けが存在します。

天下りではありますが、関連付けの結果を以下に示します。

\begin{align}
\epsilon &= \sqrt{\frac{3\delta^{A} \gamma^{A}}{bT_{m}^{A}}}= \sqrt{\frac{3\delta ^{B} \gamma ^{B}}{bT_{m}^{B}}}
\tag{57}\\
W^{A}&=\frac{6\gamma^{A} b}{\delta^{A}T_{m}^{A}}
\tag{58}\\
W^{B}&=\frac{6\gamma^{B} b}{\delta^{B}T_{m}^{B}}\tag{59}\\
M^{A}&=\frac{b(T_{m}^{A})^2\mu ^{A}}{3\delta^{A} L ^{A}}\tag{60}\\
M^{B}&=\frac{b(T_{m}^{B})^2\mu ^{B}}{3\delta^{B} L ^{B}}\tag{61}\\
\end{align}

ここで\(b\)は界面幅\(\delta\)を定義する際に現れるパラメーターで\(b=2\tanh^{-1}\left(1-2\lambda\right)\)です。例えば\(\lambda=0.1\)とすると\(b \sim 2.2\)になります。

これらの式はアレン-カーン方程式\((55)\)において単一元素の場合（\(c=0,1\)）を考えることで導出されます。

また、勾配係数\(\epsilon\)は２つの元素で共通となるので、式\((57)\)より界面幅\(\delta^{A},\delta^{B}\)の間には次の制約が課されます。

\begin{align}
\frac{\delta^{A} \gamma^{A}}{T_{m}^{A}}= \frac{\delta ^{B} \gamma ^{B}}{T_{m}^{B}}\rightarrow
\delta ^{B}=\frac{ T_{m}^{B}\gamma^{A}}{ T_{m}^{A}\gamma ^{B}}\delta^{A}\tag{62}\\
\end{align}

ただし、\(\delta^{A},\delta^{B}\)を十分に小さくとった場合、その影響は小さいためこの制約を厳密に守る必要はありません。

上式\((57)\sim(61)\)は基本的には純物質凝固の場合と似た形をしていますが、いずれも\(T_{m}\)の分だけ次元が変化しています。これはアレン-カーン方程式をエントロピー増大に関して立式しているためです。

おわりに

　今回はWBMモデルのアレン-カーン方程式の導出まで行いました。この辺りは教科書でも省略されている部分であるため、どのような仮定のもと導かれているかが分かりスッキリしました。次は濃度変化を解くための、カーン-ヒリアード方程式の導出についてまとめたいと思います。

参考文献

[1] 高木知弘ら, “フェーズフィールド法”, 養賢堂, 2012/3/2
[2] 山中晃徳ら, “Pythonによるフェーズフィールド法入門基礎理論からデータ同化の実装まで”, 丸善出版, 2023/12/15
[3] 小山敏幸ら, “フェーズフィールド法入門 (計算力学レクチャーコース) “, 丸善出版, 2013/4/13
[4] J.A. Warren, W.J. Boettinger : “Prediction of dendritic growth and microsegregation patterns in a binary alloy using the phase-field method”. Acta Metallurgica et Materialia, Volume 43, Issue 2, February 1995, Pages 689-703
[5] S.-L. Wang, R.F. Sekerka : “Thermodynamically-consistent phase-field models for solidification”. Physica D: Nonlinear Phenomena, Volume 69, Issues 1-2, 15 November 1993, Pages 189-200