MATLAB/Simulink Advent Calendar 2024 参加記事
プロローグ
年の瀬にはいり年末の業務整理に忙殺される日々。光一は仕事帰りにふと夜空を見上げると、チラホラ雪が振っていることに気がついた。
( 道理で寒いはずだ…帰ったらとりあえず炬燵で一杯やろう。)
服についた雪をはらい落とすと、一片の雪の結晶が目にとまる。その形は幾何学的な美しさを持ち、どこか神秘的な雰囲気を醸していた。
( 改めてみると不思議な形だな…どうやってこんな形が生まれるんだろう…)
仕事中は膨大な雑務に追われ、深い思考に耽ることが許されない光一にとって、降って湧いたささいな疑問は彼の脳に血を巡らせるのに十分だった。
(そうだ!MATLABを使えば何か分かるかもしれない!)
光一は逸る気持ちを抑え、足早に帰路についた。

今回の内容
はい。ということで、なぜか唐突にエセ小説など書いてしまいましたが、今回はMATLABで雪(のような形)の結晶を育成してみたいと思います。難しいことは抜きにして、エッセンスだけかいつまんで説明します。暇つぶしにどうぞ。
雪の結晶ってこんなの
雪の結晶は、大気中の水蒸気が冷やされて氷の結晶となり、成長することでさまざまな形になります。その形は、結晶が生成された上空の気温や水蒸気の量(湿度)によって決まり、自然界には一つとして同じ形のものは存在しないとも言われています。

構造上の共通点は6回対称性(6方向に延びる)を有するという点で、これは凝固時の水分子の配列に由来するとされています。また、デンドライト構造と呼ばれる樹枝状の構造を持つものが多く存在します。
今回はこの「6回対称性」を持つ「デンドライト構造」の結晶をMATLABの計算で再現してみます。
なぜこんな形になるのか
「水の温度を下げていくと0度で氷になる」ということを小学校で習いますが、実はゆーっくりと温度を下げた場合はその限りではありません。0度を下回っても、水は氷にならず水のまま存在するのです。そして何らかのきっかけ(例えば衝撃を加えるとか)で、あるとき急速に氷へと変化します。このような現象を過冷却現象と呼びます。
過冷却状態では、水が氷に変化する際に発生する熱(潜熱)の伝熱方向が通常の冷却状態とは反対になります。
熱は温度が高い方から低い方へ伝わる性質を持っているため、氷と水の界面で発生した潜熱は通常はより冷たい氷の方向に伝わります。しかし過冷却状態では、氷より水の方が温度が低いため、水の方向に熱が逃げていくわけです。「だからなんなん?」という感じかもしれませんが、実はここが最も重要なポイントです。
今、微小な凹凸を持つ氷が、水の中で成長していくことを考えましょう。通常の冷却状態の場合、潜熱は氷側に伝わるため、凹凸部分で等温線の間隔は広がってしまいます。このことは凹凸部分では熱がなかなか逃げずらいことを意味しています。この為、通常の冷却状態では、凹凸部分での氷の成長は停止し、やがて凹凸自体が消えてしまいます。
これに対して、過冷却状態の場合、潜熱は水側に伝わり、凹凸部分で等温線の間隔が小さくなります。これは凹凸部分で熱を逃がしやすいことを示しています。この為、過冷却状態では、「もっとたくさん熱を逃がしたい!」という作用が働き、凹凸がニョキニョキと成長していきます。これが雪が持つ樹枝状の形態、いわゆる「デンドライト構造」になるわけです。
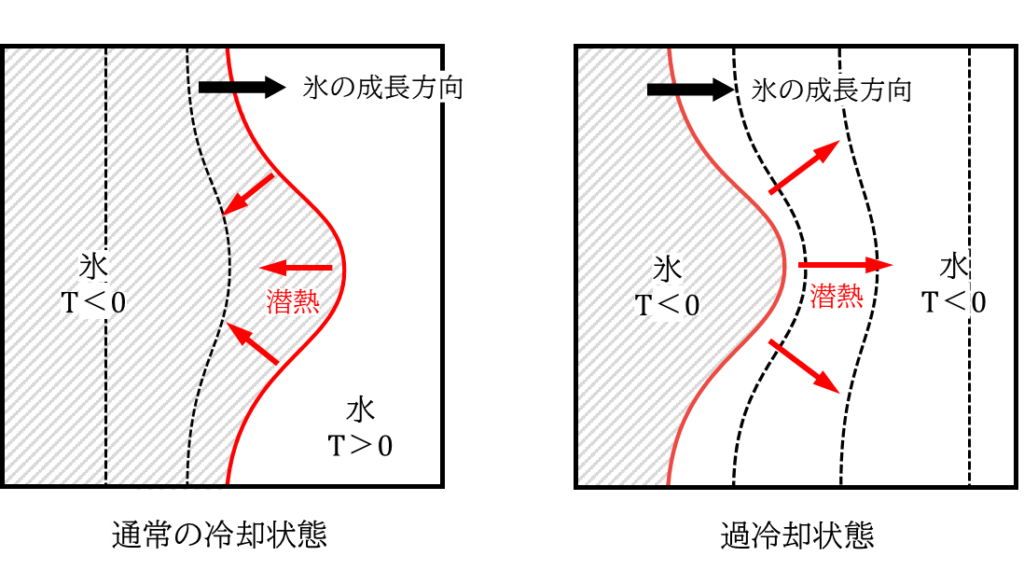
つまり、デンドライト構造の成長には「過冷却状態」と「微小な凹凸形状(=界面のゆらぎ)」の2つの要素が必要となります。
どうやって計算するのか
このような現象を計算する手法としてフェーズフィールド法があります。フェーズフィールド法ではフェーズフィールド変数と呼ばれる相状態を表す変数\(\phi\)を導入し、系の自由エネルギーを減少させる方向に変化させることで、組織の時間発展を予測します。とても奥が深いので、深入りはしませんが、今回解くべき方程式だけ示しておきます。

上記のような式を差分法などで離散化して解きます。詳細に興味はある方は以下の記事などご参考ください。
計算結果
以下に計算結果を示します。まあ、なんとくそれっぽいんじゃないでしょうか…。じっと見つめて楽しみましょう。
MATLABコード
最後に今回用いたコードを示します。フェーズフィールド変数に加えて、温度・潜熱も同時に描画されます。
% 初期化処理 --------------------------------------------------------------
clc; close all;
clear all;
% パラメーター設定 --------------------------------------------------------
% 時間・空間ステップ設定
dt = 5.0e-12; % タイムステップ[s]
maxstep = 45000; % 最大ステップ数
dx = 2.0e-08; % 差分格子点の間隔[m]:20[um]
dy = dx; % 差分格子点の間隔[m]
nx = 750; % 差分格子点数
ny = nx; % 差分格子点数
xmax = dx * nx ;
xmin = 0;
ymax = dy * ny;
ymin = 0;
xl = xmin:dx:xmax-dx;
yl = ymin:dy:ymax-dy;
% 物性値の設定
T_0 = 1511.2; % 系の温度 [K]
T_melt = 1728.0; % Niの融点 [K]
gamma = 0.37; % 界面エネルギー [J/m2]
K = 84.01; % 熱伝導率 [W/(mK)]
cv = 5.42e+06; % 比熱 [J/K]
latent = 2.35e+09; % 潜熱 [J/mol]
mu = 2.0; % 界面カイネティック係数 [m/(Ks)]
lamb = 0.1; % 界面厚みの閾値
b = 2.0 * atanh(1.0 - 2.0 * lamb);
delta = 4.0 * dx; % 界面幅[m]
sc = cv *(T_melt-T_0)/latent; % 過冷度
% 物性値の変換
w = 6.0 * gamma * b / delta; % エネルギー障壁[J/m3]
mp = b * T_melt * mu / (3.0 * delta * latent); % フェーズフィールドモビリティー
abar = sqrt(3.0*delta*gamma/b); % 基準となる勾配係数
xi = 0.01; % 異方性強度
k = 6; % 異方性モード
theta_0 = 0; % 優先成長方向
% 変数宣言
phi = zeros(nx,ny);
phi_new = zeros(nx,ny);
dphi = zeros(nx,ny);
q = zeros(nx,ny);
nvec_x = zeros(nx,ny);
nvec_y = zeros(nx,ny);
T = zeros(nx,ny);
dT = zeros(nx,ny);
T_new = zeros(nx,ny);
dg = zeros(nx,ny);
theta = zeros(nx,ny);
thetadeg = zeros(nx,ny);
a = zeros(nx,ny);
A = zeros(nx,ny);
B = zeros(nx,ny);
dadx= zeros(nx,ny);
dady = zeros(nx,ny);
dphidx = zeros(nx,ny);
dphidy = zeros(nx,ny);
lap_phi = zeros(nx,ny);
lap_temp = zeros(nx,ny);
% 安定条件の確認
theta_test = 0:2*pi/100:2*pi;
amax = max(abar * (1 + xi * cos(k*(theta_test-theta_0))));% 勾配係数の最大値を計算する。
dt1 = (1/(2*amax^2*mp))*(dx^2*dy^2)/(dx^2+dy^2);
dt2 =(cv/(2*K))*(dx^2*dy^2)/(dx^2+dy^2);
if dt > min(dt1,dt2)
error('タイムステップが安定条件を満たしていません。')
end
% 可視化設定 -----------------------------------------------------------------
% ファイル名
paramstr =['abar = ', num2str(abar, '%.1e'), ', w = ', num2str(w, '%.1e'), ...
', dg = ', num2str(1, '%.2f'), ', mp = ', num2str(mp, '%.2f'),...
', xi = ', num2str(xi, '%.2f'), ', k = ', num2str(k, '%.2f'),...
', theta_0 = ', num2str(theta_0, '%.2f'),', Delta = ', num2str(sc, '%.2f'), ];
filename = [paramstr,'.mp4'];
% VideoWriter オブジェクトの初期化
outputVideo = VideoWriter(filename, 'MPEG-4');
outputVideo.FrameRate = 30; % フレームレートの設定
open(outputVideo);
% グラフの配置調整
figure('Visible', 'off', 'Position', [100, 100, 1800, 600], 'Color', 'white');
ax1 = axes('Position', [0.05, 0.1, 0.28, 0.8]);
ax2 = axes('Position', [0.37, 0.1, 0.28, 0.8]);
ax3 = axes('Position', [0.69, 0.1, 0.28, 0.8]);
[Y, X] = meshgrid(yl, xl); % X, Yグリッドを生成
% レンジの決定
xmin = min(xl);
xmax = max(xl);
ymin = min(yl);
ymax = max(yl);
% テキストボックスのテキスト作成
str_1 = ['$ \bar{a} = ', num2str(abar, '%.1e'), ...
', \, W = ', num2str(w, '%.1e'), ...
', \, M_p = ', num2str(mp, '%.1f'), '$'];
str_2 = ['$ \xi = ', num2str(xi, '%.2f'), ...
', \, k = ', num2str(k, '%.1f'), ...
', \, \theta_0 = ', num2str(theta_0, '%.1f'), ...
', \, \Delta = ', num2str(sc, '%.2f'), '$'];
str = {str_1, str_2};
% テキストボックスの位置とサイズを定義
dim1 = [0.12 0.1 0.18 0.12];
dim2 = [0.44 0.1 0.18 0.12];
dim3 = [0.76 0.1 0.18 0.12];
% テキストボックスを図に追加
annotation('textbox', dim1, 'String', str, 'FitBoxToText', 'on', ...
'BackgroundColor', 'none', 'EdgeColor', 'none', 'FontSize', 12, 'Interpreter', 'latex');
annotation('textbox', dim2, 'String', str, 'FitBoxToText', 'on', ...
'BackgroundColor', 'none', 'EdgeColor', 'none', 'FontSize', 12, 'Interpreter', 'latex');
annotation('textbox', dim3, 'String', str, 'FitBoxToText', 'on', ...
'BackgroundColor', 'none', 'EdgeColor', 'none', 'FontSize', 12, 'Interpreter', 'latex');
% 初期条件 ----------------------------------------------------------------
r0 = 2 * dx;
for j = 1 : ny
for i = 1 : nx
%r = sqrt((i*dx)^2 +((ny-j)*dy)^2) - r0;% 原点に核生成
r = sqrt( ((i-(nx/2))*dx)^2 +((j-(ny/2)) * dy)^2 ) - r0;% 中央に核生成
phi(i, j) = 0.5 * (1 - tanh(sqrt(2 * w) / (2 * abar) * r)); % フェーズフィールド変数の初期分布
T(i,j,1) = T_0 + phi(i,j) * (T_melt - T_0); % 温度の初期分布
end
end
% 時間発展 ----------------------------------------------------------------
for step = 1 : maxstep
step
% 界面異方性を考慮した勾配係数計算のループ
for i = 1 : nx
for j = 1 : ny
% 隣接節点
ip = i + 1;
im = i - 1;
jp = j + 1;
jm = j - 1;
% ノイマン条件
if ip > nx
ip = nx;
end
if im < 1
im = 1;
end
if jp > ny
jp = ny;
end
if jm < 1
jm = 1;
end
% 法線ベクトル計算
nvec_x(i,j) = -(phi(ip,j) - phi(im,j))/(2*dx);
nvec_y(i,j) = -(phi(i,jp) - phi(i,jm))/(2*dy);
% 法線ベクトルとX軸が成す角度の計算。基底ベクトルの正負に応じて割り当てる角度範囲を変える。
if nvec_x(i,j)>0 && nvec_y(i,j)>0
theta(i,j) = atan(nvec_y(i,j)/nvec_x(i,j));
elseif nvec_x(i,j)<0 && nvec_y(i,j)>0
theta(i,j) = atan(nvec_y(i,j)/nvec_x(i,j)) + pi;
elseif nvec_x(i,j)<0 && nvec_y(i,j)<0
theta(i,j) = atan(nvec_y(i,j)/nvec_x(i,j)) + pi;
elseif nvec_x(i,j)>0 && nvec_y(i,j)<0
theta(i,j) = atan(nvec_y(i,j)/nvec_x(i,j)) + 2*pi;
elseif nvec_x(i,j)>0 && nvec_y(i,j)==0
theta(i,j) = 0;
elseif nvec_x(i,j)==0 && nvec_y(i,j)>0
theta(i,j) = pi/2;
elseif nvec_x(i,j)<0 && nvec_y(i,j)==0
theta(i,j) = pi;
elseif nvec_x(i,j)==0 && nvec_y(i,j)<0
theta(i,j) = 3*pi/2;
end
% 勾配エネルギー係数a
a(i,j) = abar * (1 + xi * cos(k*(theta(i,j)-theta_0)));
% 1階微分
dphidx(i,j) = (phi(ip,j)-phi(im,j))/(2*dx);
dphidy(i,j) = (phi(i,jp)-phi(i,jm))/(2*dy);
% 9点ラプラシアン
lap_phi(i,j) = (2 * (phi(ip,j) + phi(im,j) + phi(i,jp) + phi(i,jm)) ...
+ phi(ip,jp) + phi(im,jm) + phi(im,jp) + phi(ip,jm) - 12 * phi(i,j)) / (3 * dx^2);
lap_temp(i,j) = (2 * (T(ip,j) + T(im,j) + T(i,jp) + T(i,jm))...
+ T(ip,jp) + T(im,jm) + T(im,jp) + T(ip,jm) - 12 * T(i,j)) / (3 * dx^2);
end
end
% フェーズフィールド変数、温度場の時間発展ループ
for i = 1 : nx
for j = 1 : ny
% 隣接節点
ip = i + 1;
im = i - 1;
jp = j + 1;
jm = j - 1;
% ノイマン条件
if ip > nx
ip = nx;
end
if im < 1
im = 1;
end
if jp > ny
jp = ny;
end
if jm < 1
jm = 1;
end
% aの微係数計算
A(i, j) = a(i,j)*abar*k*xi*sin(k*(theta(i,j)-theta_0))*dphidy(i,j);
B(i, j) = a(i,j)*abar*k*xi*sin(k*(theta(i,j)-theta_0))*dphidx(i,j);
dadx(i,j) = (a(ip,j)-a(im,j))/(2*dx);
dady(i,j) = (a(i,jp)-a(i,jm))/(2*dy);
% 化学的駆動力の増分の計算
dg(i,j) = latent * (T(i,j)-T_melt)/T_melt;
% フェーズフィールド変数の増分の計算
% エネルギー密度関数1
% dphi(i,j) =...
% -6*dg(i,j)*phi(i,j)*(1-phi(i,j)) - 2*w*phi(i,j)*(1-phi(i,j))*(1-2*phi(i,j))...
% +2*a(i,j,step)*(dadx(i,j)*dphidx(i,j)+dady(i,j)*dphidy(i,j))...
% +a(i,j,step)^(2)*lap_phi(i,j)...
% +(A(ip,j)-A(im,j))/(2*dx)-((B(i,jp)-B(i,jm))/(2*dy));
% エネルギー密度関数2
noize = 0.3*(2 * rand - 1);
dphi(i,j) =...
-30*dg(i,j)*phi(i,j)^2*(1-phi(i,j))^2 - 2*w*phi(i,j)*(1-phi(i,j))*(1-2*phi(i,j))...
+2*a(i,j)*(dadx(i,j)*dphidx(i,j)+dady(i,j)*dphidy(i,j))...
+a(i,j)^(2)*lap_phi(i,j)...
+(A(ip,j)-A(im,j))/(2*dx)-((B(i,jp)-B(i,jm))/(2*dy))...
+ 4 * w * phi(i,j)*(1-phi(i,j))* noize;
% フェーズフィールド変数の時間発展
phi_new(i,j) = phi(i,j) + dt * mp * dphi(i,j);
% 温度場の増分の計算
%q(i,j) = 6*latent*phi(i,j)*(1-phi(i,j))*(phi_new(i,j)-phi(i,j))/dt;
q(i,j) = 30*latent*phi(i,j)^2*(1-phi(i,j))^2*(phi_new(i,j)-phi(i,j))/dt;% 9点ラプラシアン
dT(i,j) = (1 / cv)*(K* lap_temp(i,j) +q(i,j));
% 温度場の時間発展
T_new(i,j) = T(i,j) + dt *dT(i,j);
end
end
% タイムステップを置き換える
phi = phi_new;
T = T_new;
% 動画保存
if step == 1
plotconfig(xl, yl, xmin,xmax, ymin,ymax,step,dt,ax1,ax2,ax3,T_0,T_melt,phi,T,q)
v = VideoWriter(filename,'MPEG-4');
v.FrameRate = 100;
open(v);
elseif mod(step, 60) == 0
plotconfig(xl, yl, xmin,xmax, ymin,ymax,step,dt,ax1,ax2,ax3,T_0,T_melt,phi,T,q)
frame = getframe(gcf);
writeVideo(v,frame);
end
end
% 動画ファイルを閉じる
close(v);
% 以下ローカル関数---------------------------------------------------------------
% 可視化
function [] = plotconfig(xl, yl, xmin,xmax, ymin,ymax,step,dt,ax1,ax2,ax3,T_0,T_melt,phi,T,q)
% Phase-field サブプロット
axes(ax1);
cla(ax1);
imagesc(xl, yl, imrotate(phi(:,:), 90), [0, 1]);
title(ax1, sprintf('phase-field $\\phi$ at %.3e [s]', step*dt), 'Interpreter', 'latex');
cb1 = colorbar(ax1);
title(cb1, '$\phi$', 'Interpreter', 'latex');
axis(ax1, 'equal');
axis(ax1, 'tight');
xlabel('$$x\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
ylabel('$$y\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
xticks(linspace(xmin, xmax, 6)); % x軸の目盛りを設定
yticks(linspace(ymin, ymax, 6)); % y軸の目盛りを設定
ax1.XAxis.TickLabelFormat = '%,.1f';
ax1.YAxis.TickLabelFormat = '%,.1f';
set(ax1, 'YDir', 'normal', 'FontName', 'Times New Roman', 'FontSize', 12,'LineWidth',1.2);
% 温度場 サブプロット
T_min = T_0;
T_max = T_melt;
axes(ax2);
cla(ax2);
imagesc(xl, yl, imrotate(T(:,:), 90), [T_min, T_max]);
title(ax2, sprintf('temperature $T \\rm{[K]}$ at %.3e [s]', step*dt), 'Interpreter', 'latex');
cb2 = colorbar(ax2);
title(cb2, '$T$', 'Interpreter', 'latex');
axis(ax2, 'equal');
axis(ax2, 'tight');
xlabel('$$x\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
ylabel('$$y\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
xticks(linspace(xmin, xmax, 6)); % x軸の目盛りを設定
yticks(linspace(ymin, ymax, 6)); % y軸の目盛りを設定
ax2.XAxis.TickLabelFormat = '%,.1f';
ax2.YAxis.TickLabelFormat = '%,.1f';
set(ax2, 'YDir', 'normal', 'FontName', 'Times New Roman', 'FontSize', 12,'LineWidth',1.2);
% 潜熱コンター
q_min = -3.106811707055531e+17;
q_max = 2.210685380238862e+19;
axes(ax3);
cla(ax3);
imagesc(xl, yl, imrotate(q(:,:), 90), [q_min, q_max]);
title(ax3, sprintf('latent heat $q \\rm{[W/m^3]}$ at %.3e [s]', step*dt), 'Interpreter', 'latex');
cb3 = colorbar(ax3);
title(cb3, '$q$', 'Interpreter', 'latex');
axis(ax3, 'equal');
axis(ax3, 'tight');
xlabel('$$x\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
ylabel('$$y\rm{[m]}$$', 'Interpreter', 'latex', 'FontSize', 14);
xticks(linspace(xmin, xmax, 6)); % x軸の目盛りを設定
yticks(linspace(ymin, ymax, 6)); % y軸の目盛りを設定
ax3.XAxis.TickLabelFormat = '%,.1f';
ax3.YAxis.TickLabelFormat = '%,.1f';
set(ax3, 'YDir', 'normal', 'FontName', 'Times New Roman', 'FontSize', 12, 'LineWidth', 1.2);
% 新しいプロットの時、軸設定を保持したまま前のグラフィックスオブジェクトを消去
set(gca,'nextplot','replacechildren');
endおわりに
今回はかいつまんだ説明で、それっぽい計算を行いましたが、実際の雪の結晶を正確に予測するのはほぼ不可能とされています。なぜなら、雪の結晶の表面エネルギー状態は温度の関数であり、大気中のどの温度領域をどのぐらいのスピードで通過するのかによって、取り得る形態が次々と変化するためです。
逆に言うと、ある雪の結晶の形が完全に予測できた場合、雪が落ちてくる大気中の経路の温度分布が完全に明らかになるということを意味します。夢みたいな話ですよね。
とはいえ、1980年代にこの計算手法が確立された際には、組織予測の研究者たちの間で大きく話題になったようで、今なお、勢力的に研究がなされている分野となっています。
参考文献
[1] 高木 知弘ら, “フェーズフィールド法”, 養賢堂, 2012/3/2
[2] Wikipedia, https://ja.wikipedia.org/wiki/%E9%9B%AA%E7%89%87#:~:text=%E9%9B%AA%E7%89%87%EF%BC%88%E3%81%9B%E3%81%A3%E3%81%BA%E3%82%93%EF%BC%89%E3%81%AF%E3%80%81,%E3%81%93%E3%81%A8%E3%81%A7%E6%A0%B8%E7%94%9F%E6%88%90%E3%81%99%E3%82%8B%E3%80%82



コメント