差分法で二次元非定常熱伝導方程式を解く〖MATLABコード付き〗

はじめに

　二次元非定常熱伝導方程式

離散化

　左辺をオイラー陽解法（前進差分法）で離散化すると以下のように書ける。

右辺は二階微分を中心差分法で離散化すると

ここで正方格子を想定し、\(h=Δx=Δy\)とする。以上、式\((2)\)、式\((3)\)より、式全体は

\(T(t+\Delta t)\)のみ左辺に残すと、

となる。これが離散化された非定常熱伝導方程式である。式\((5)\)より次ステップの温度は「周囲隣接節点の平均温度」と「中心節点の温度」の差分に比例して増加していくことが分かる。

行列形式

　離散化された非定常熱伝導方程式（式\((5)\)）は温度に関して線形となっており、行列を用いるとよりシンプルに記述できる。

このように行列で表した場合、その時間発展行列は中心節点要素が\(1-\frac{4k\Delta t}{c\rho h}\)、周囲隣接節点要素が\(\frac{k\Delta t}{c\rho h}\)となる。 例えば、これを3*3の2次元格子（下図）に拡張すると、

と記述できる。ここで境界節点は温度固定で与えるものとし、その節点部分のみ１と置くようにしている。これは3*3の単純な例だが、実際にはこれをn*nの格子へ拡張することで、温度場を解くことができる。

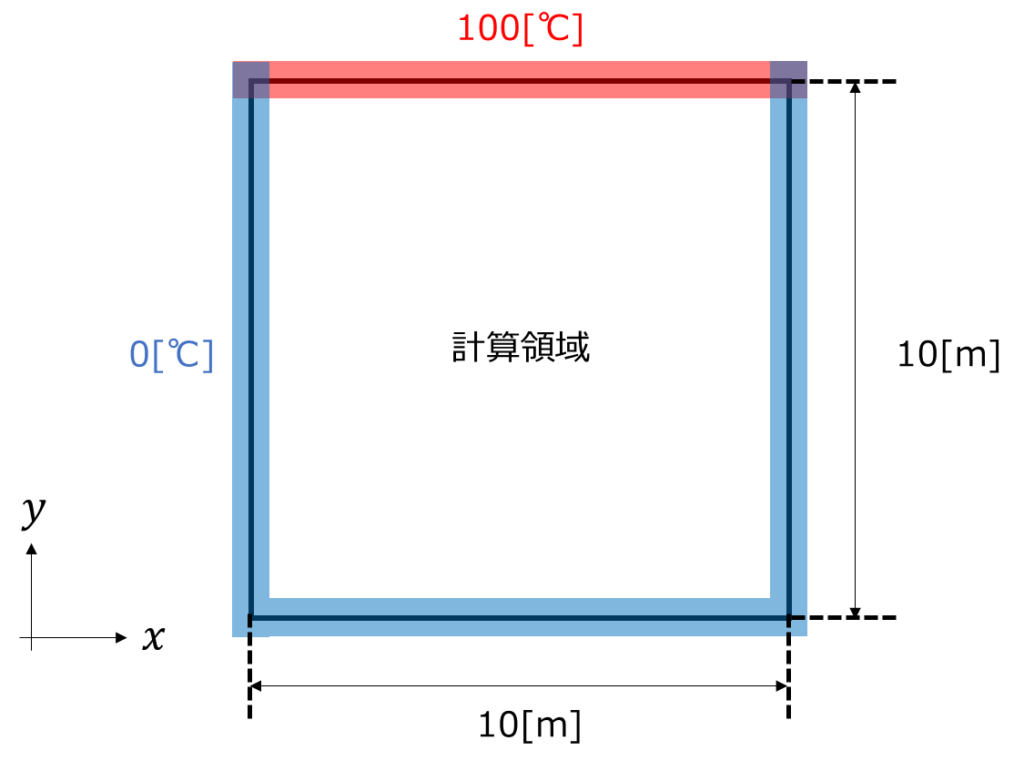
境界条件の設定

　上辺が100[℃]、その他の辺が0[℃]の境界を持ち、内部温度が\(t=0[s]\)で0[℃]の二次元領域の非定常解を求める。なお内部で発熱はないものとする。（\(q=0\)）

Matlabソースコード

　ソースコードはこちらにアップしています。

% 初期化
clc; clear all;

% グローバル変数宣言
global dt n ita L x y

% パラメーター
L = 10;% 計算領域
n = 30;% 要素数
dL = L / n;% 要素サイズ
c = 1;% 比熱
rho = 1;% 密度
k = 1;% 熱伝導率
alpha = k / (c * rho);% 熱拡散率

t_total = 10;% SIM計算時間
dt = 0.01;% タイムステップ
ita = t_total / dt;% 反復数

% 座標の生成
x = 0 : L / n : L;
y = L : - L / n : 0;
[X, Y] = meshgrid(x, y);

% 配列確保
T2d = zeros(n, n, ita);
wall_2d = zeros(n, n);

% 熱境界条件
T1 = 100;% 北側
T2 = 0;% 東側
T3 = 0;% 南側
T4 = 0;% 西側

% 境界条件を設定と行列の作成
[T2d, wall_2d] = DefineWall(T2d, wall_2d, T1, T2, T3, T4);

% 温度ベクトルの構築
T1d = zeros(n * n, ita);
for i = 1 : ita
    T1d(:, i) = reshape(T2d(:, :, i).', [n * n, 1]);% リシェイプの前に転置しておく
end
wall_1d = reshape(wall_2d.', [n * n, 1]);

% 時間発展行列の構築
A = TransitionMatrix(wall_1d, alpha, dL);

% 時間発展
for i = 2 : ita
    
    % 時間発展
    T1d(:, i) = A * T1d(:, i - 1);
    T2d(:, :, i) = (reshape(T1d(:, i), [n, n])).';
    
    % コマンドウィンドウへの出力
    txt = ['ita = ',num2str(i),' / ',num2str(ita)];
    disp(txt);
    
    % 可視化
    vis_contour('temp.gif', i, T2d(:, :, i), 0, 100, 1);
    
end

%% 以下関数

function[T2d, wall_2d] = DefineWall(T2d, wall_2d, T1, T2, T3, T4)

% グローバル変数呼び出し
global n

% 壁行列
% 1|2|3
% 8|0|4
% 7|6|5

for j = 1 : n
    for i = 1 : n
        if i == 1 && j == 1% 左上
            T2d(i, j, :) = T1;
            wall_2d(i, j) = 1;
        elseif i == 1 && j == n% 右上
            T2d(i, j, :) = T1;
            wall_2d(i, j) = 3;
        elseif i == n && j == n% 右下
            T2d(i, j, :) = T3;
            wall_2d(i, j) = 5;
        elseif i == n && j == 1% 左下
            T2d(i, j, :) = T3;
            wall_2d(i, j) = 7;
        elseif i == 1
            T2d(i, j, :) = T1;
            wall_2d(i, j) = 2;
        elseif j == n
            T2d(i, j, :) = T3;
            wall_2d(i, j) = 4;
        elseif i == n
            T2d(i, j, :) = T2;
            wall_2d(i, j) = 6;
        elseif j == 1
            T2d(i, j, :) = T4;
            wall_2d(i, j) = 8;
        end
    end
end

end


function[A] = TransitionMatrix(wall_1d, alpha, dL)

% グローバル変数呼び出し
global n dt

% 壁行列
% 1|2|3
% 8|0|4
% 7|6|5

A = zeros(n * n, n * n);
for i = 1 : n * n
    if wall_1d(i, 1) == 1% 角は二つの境界条件の平均をとる。
        A(i, i + 1) = 1 / 2;
        A(i, i + n) = 1 / 2;
    elseif wall_1d(i, 1) == 2% 北側壁
        A(i, i) = 1;
    elseif wall_1d(i, 1) == 3% 角は二つの境界条件の平均をとる。
        A(i, i - 1) = 1 / 2;
        A(i, i + n) = 1 / 2;
    elseif wall_1d(i, 1) == 4% 東側壁
        A(i, i) = 1;
    elseif wall_1d(i, 1) == 5% 角は二つの境界条件の平均をとる。
        A(i, i - 1) = 1 / 2;
        A(i, i - n) = 1 / 2;
    elseif wall_1d(i, 1) == 6% 南側壁
        A(i, i) = 1;
    elseif wall_1d(i, 1) == 7% 角は二つの境界条件の平均をとる
        A(i, i + 1) = 1 / 2;
        A(i, i - n) = 1 / 2;
    elseif wall_1d(i, 1) == 8% 西側壁
        A(i, i) = 1;
    elseif wall_1d(i, 1) == 0% 壁でないならば
        A(i, i) = 1 - 4 * dt * alpha / dL^2;
        A(i, i - 1) = dt * alpha / dL^2;
        A(i, i + 1) = dt * alpha / dL^2;
        A(i, i - n) = dt * alpha / dL^2;
        A(i, i + n) = dt * alpha / dL^2;
    end
end

end

function[] = vis_contour(filename, timestep, u, maxrange, minrange, fignum)

% グローバル変数呼び出し
global dt L x y

figure(fignum);
h = imagesc(x, y, u);

h.AlphaData = isfinite(u); % NaNやInfを透明にする
title(['time = ', num2str(timestep * dt, '%.3f')]);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 16);
axis equal; axis tight; axis on;
xlabel('x')
ylabel('y')
view(0, 270); % 視点の設定
xticks(0 : round(L / 5) : L);
yticks(0 : round(L / 5) : L);
fig=gcf;
fig.Color='white';

colorbar;
caxis([maxrange minrange])
frame = getframe(fignum);
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if timestep == 2
    imwrite(imind, cm, filename, 'gif', 'DelayTime', 0.001, 'Loopcount', inf);
elseif rem(timestep, 10) == 0
    imwrite(imind, cm, filename, 'gif', 'DelayTime', 0.001, 'WriteMode', 'append');
end

end

計算結果

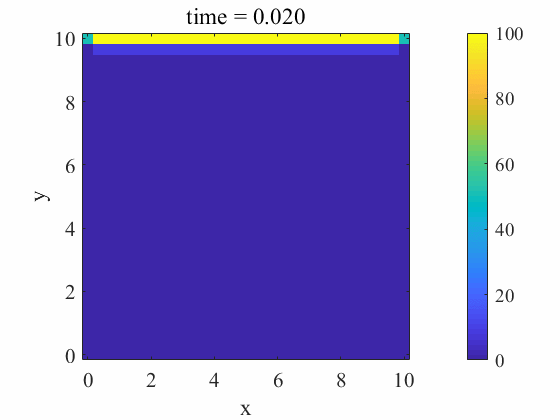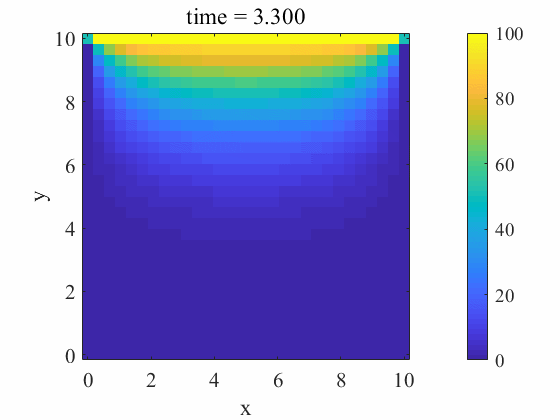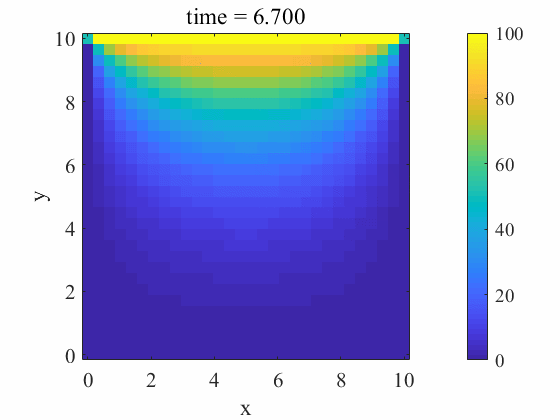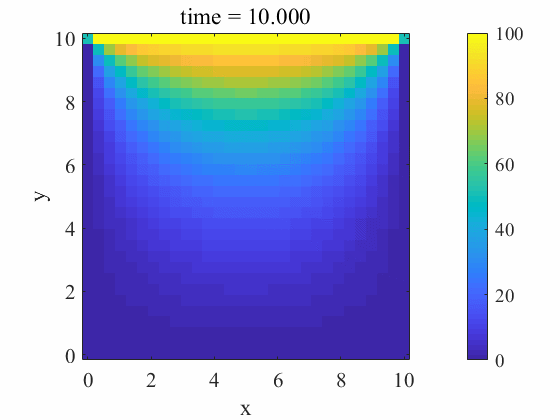
おわりに

　今回は2次元非定常熱伝導方程式の数値解を求めました。非定常熱伝導方程式（放物型偏微分方程式）は離散化すると線形マトリクスになるため計算は容易でした。 今後は解の安定性（適切なタイムステップやメッシュ解像度の決め方など）について調べてみたいと思います。