はじめに
前回は様々な高次の線形スキームを実装し、クーラン数違いでの評価を行いました。しかしながら、解くべき方程式は移流速度が定数となる線形方程式に限定していました。流体シミュレーションで用いられるNS方程式は移流速度が変数となる非線形方程式です。
そこで今回は「数値流束による保存型表示」を導入することで今までのスキームを見通しよく整理し、そのうえで非線形方程式への対応方法についてまとめていきたいと思います。
数値流束による保存型表示
ここまでの記事では以下の一次元移流方程式について差分法の様々なスキームで離散化し、その数値解を求めてきました。
\frac{\partial q}{\partial t}+c\frac{\partial q}{\partial x}= 0\tag{1}
\end{align}
ここで定数\(c\)を微分の中に入れて\(f=cq\)と表現すると以下のように書けます。
\frac{\partial q}{\partial t}+\frac{\partial f}{\partial x}= 0 \qquad (f=cq) \tag{2}
\end{align}
\(f\)は「流束(フラックス)」と呼ばれ「単位時間あたりに単位面積を通過する物理量\(q\)の総量」を意味します。
この流束\(f\)について空間離散化を考えてみましょう。前回の記事までは\(q\)について差分法を用いて各格子点\((\cdots,j-1,j,j+1\cdots)\)で離散化してきましたが、今回、流束\(f\)の離散化に関しては少し方法を変えます。
以下のように各格子点を中心にもつセルを考え、その界面に仮想的な格子点\((\cdots,j-\frac{1}{2},j+\frac{1}{2}\cdots)\)を設置し、そこで流束\(f\)を離散化することとします。

q^{n+1}_{j}=q^{n}_{j}-\frac{\Delta t}{\Delta x}\left( \tilde{f}^{n}_{j+\frac{1}{2}}-\tilde{f}^{n}_{j-\frac{1}{2}}\right) \tag{3}
\end{align}
このように仮想格子点上\((\cdots,j-\frac{1}{2},j+\frac{1}{2}\cdots)\)で離散化された流束を「数値流束」と呼びチルダ記号を付けて\(\tilde{f^{n}}\)と記述します。(一方で通常の格子上で離散化された流束\(f^{n}\)は物理流束と呼ばれ区別されます。)
冒頭で述べた通り、流束とは「単位時間あたりに単位面積を通過する物理量\(q\)の総量」でした。したがって、界面で定義された「数値」流束は「各セルに界面から単位時間あたりに流入(流出)する物理量\(q\)の総量」と考えてよいでしょう。
数値流束についてより直感的な理解を得るため、式\((3)\)の両辺に\(\Delta x \)をかけ以下のように変形します。
q^{n+1}_{j}\Delta x=q^{n}_{j}\Delta x- \tilde{f}^{n}_{j+\frac{1}{2}}\Delta t+\tilde{f}^{n}_{j-\frac{1}{2}}\Delta t \tag{4}
\end{align}
右辺第一項はセル\(j\)がもつ物理量\(q\)の総和、第二項、第三項は\(\Delta t\)あたりにセル\(j\)に流出・流入する物理量の総和を示します。したがって上式は「現タイムステップにおける物理量の流出・流入の正味が次タイムステップにおけるそのセルの物理量となる」ことを意味しています。これはセル単位での物理量の保存則そのものです。ゆえに数値流束の考え方を導入した式\((3)\)を移流方程式の「保存型表示」と呼びます。
移流方程式が物理量の保存則を表す例としては連続の式があります。連続の式は流体の質量保存則を示しているのでした。式\((1)\)において物理量\(q\)を密度\(\rho\)、移流速度\(c\)を流速\(u\)で表すと連続の式になります。
今回は差分法を起点に数値流束の考えを取り入れることでセル単位での保存則を考慮した離散化を行いましたが、これは結果的に有限体積法による離散化と同等になります。言い換えると有限体積法を差分法的に解釈した時に現れる概念が数値流束と言えます。
数値流束の計算
次に数値流束\(\tilde{f^{n}}_{j+\frac{1}{2}}\)の具体的な中身について考えてみます。物理量はあくまで通常の格子点上\((\cdots,j-1,j,j+1\cdots)\)で定義されるため、\(\tilde{f}^{n}_{1+\frac{1}{2}}\)は通常の格子点上の物理流束\(f^{n}_{j},f^{n}_{j+1},\cdots \)などを用いて表されます。
例えば、最もシンプルには以下のように隣接格子の平均値で表現するのが直感的です。
\tilde{f}^{n}_{j+\frac{1}{2}}=\frac{f^{n}_{j} +f^{n}_{j+1}}{2} =c\frac{q^{n}_{j} +q^{n}_{j+1}}{2} \tag{5}
\end{align}
同様に\(\tilde{f^{n}}_{j-\frac{1}{2}}\)は
\tilde{f}^{n}_{j-\frac{1}{2}}=\frac{f^{n}_{j-1} +f^{n}_{j}}{2} =c\frac{q^{n}_{j-1} +q^{n}_{j}}{2} \tag{6}
\end{align}
これらを式\((3)\)に代入すると以下の式が得られます。
q^{n+1}_{j}&=q^{n}_{j}-\frac{\Delta t}{\Delta x}\left( \tilde{f}^{n}_{j+\frac{1}{2}}-\tilde{f}^{n}_{j-\frac{1}{2}}\right) \\
&=q^{n}_{j}-\frac{ \Delta t}{\Delta x}\left(c\frac{q^{n}_{j} +q^{n}_{j+1}}{2}-c\frac{q^{n}_{j-1} +q^{n}_{j}}{2} \right) \\
&=q^{n}_{j}-\frac{ c\Delta t}{\Delta x}\left(\frac{q^{n}_{j+1} +q^{n}_{j-1}}{2} \right)\\ \tag{7}
\end{align}
上式は中心差分法による離散化結果と一致します。
今度は以下のように数値流束\(\tilde{f}^{n}_{j+\frac{1}{2}},\tilde{f}^{n}_{j-\frac{1}{2}}\)を一個左の格子で表すこととしてみます。
\tilde{f}^{n}_{j+\frac{1}{2}}=f^{n}_{j} =c q^{n}_{j} \tag{8}
\end{align}
\tilde{f}^{n}_{j-\frac{1}{2}}=f^{n}_{j-1} =c q^{n}_{j-1} \tag{9}
\end{align}
すると式\((3)\)は以下のように書けます。
q^{n+1}_{j}&=q^{n}_{j}-\frac{\Delta t}{\Delta x}\left( \tilde{f}^{n}_{j+\frac{1}{2}}-\tilde{f}^{n}_{j-\frac{1}{2}}\right) \\
&=q^{n}_{j}-\frac{ \Delta t}{\Delta x}\left(cq^{n}_{j}-cq^{n}_{j-1} \right) \\
&=q^{n}_{j}-\frac{ c\Delta t}{\Delta x}\left(q^{n}_{j} -q^{n}_{j-1} \right)\\ \tag{10}
\end{align}
上式は\(c\geq 0\)とした場合の風上差分法による離散化結果と一致します。
このように保存型表示では離散化スキームの違いは数値流束の表現方法の違いとして統一的に整理されます。これによりプログラムもスッキリ書くことが出来るようになります。対応するMATLABコードをgithubにアップロードしましたので、よろしければご覧ください。
最後に各スキームの数値流束表記をまとめます。\(\nu\)はクーラン数\(\frac{c\Delta t}{\Delta x}\)です。風上差分法以外はステンシル(利用する離散点)に対して対称な手法なので、情報の伝搬方向に依存せず利用できます。

輸送速度が変数となる非線形問題の場合
保存型表示の導入の利点はプログラムがすっきりするという以上に、以下の非粘性Bugers方程式にように輸送速度が変数となったときに正しい解を与えることが出来るという点にあります。
\frac{\partial q}{\partial t}+q\frac{\partial q}{\partial x}= 0\tag{11}
\end{align}
非粘性Bugers方程式はNS方程式の非定常項・移流項を取り出してきた方程式であり、この部分を正確に解くことは流体シミュレーションにおいてとても大事です。
では保存型・非保存型で解にどのような差が生じるのか確認してみます。
式\((11)\)ついて非保存型の状態で通常の1次精度風上差分法で離散化すると以下のように書けます。全領域で\(q\geq 0\)を仮定すると
&\frac{q_{j}^{n+1}-q_{j}^{n}}{\Delta t}+q_{j}^{n}\frac{q_{j}^{n}-q_{j-1}^{n}}{\Delta x}= 0 \\
&\Leftrightarrow
q_{j}^{n+1}=q_{j}^{n}-\frac{q_{j}^{n}\Delta t}{\Delta x}(q_{j}^{n}-q_{j-1}^{n})
\tag{12}
\end{align}
同様に全領域で\(q < 0\)の場合は風上が入れ替わり以下のように書けます。
q_{j}^{n+1}=q_{j}^{n}-\frac{q_{j}^{n}\Delta t}{\Delta x}(q_{j+1}^{n}-q_{j}^{n})
\tag{13}
\end{align}
式\((12)\)と式\((13)\)を組み合わせると移流方向に依存しない風上差分は以下のように書けます。
q_{j}^{n+1}=q_{j}^{n}-\frac{q_{j}^{n}+|q_{j}^{n}|}{2}\frac{\Delta t}{\Delta x}(q_{j}^{n}-q_{j-1}^{n})-\frac{q_{j}^{n}-|q_{j}^{n}|}{2}\frac{\Delta t}{\Delta x}(q_{j+1}^{n}-q_{j}^{n})
\tag{14}
\end{align}
上式が式\((11)\)の非保存型表示です。絶対値記号を用いることで常に風上差分になるように採用するステンシルを調整しています。
一方で式\((11)\)を保存型にすると以下のように書けます。
&\frac{\partial q}{\partial t}+q\frac{\partial q}{\partial x}= 0\\
&\Leftrightarrow
\frac{\partial q}{\partial t}+\frac{\partial }{\partial x}\left(\frac{q^2}{2}\right)= 0\\
&\Leftrightarrow
\frac{\partial q}{\partial t}+\frac{\partial f}{\partial x}= 0
\tag{15}
\end{align}
上記のように非粘性Bugers方程式の場合、流束\(f\)は\(f=\frac{q^2}{2}\)として与えることが出来ることが分かります。
上式について風上差分法で離散化を施します。全領域で\(q\geq 0\)を仮定すると\(\tilde{f}^{n}_{j+\frac{1}{2}}=\frac{(q^{n}_{j})^2}{2},\tilde{f}^{n}_{j-\frac{1}{2}}=\frac{(q^{n}_{j-1})^2}{2}\)と書けるので
q^{n+1}_{j}&=q^{n}_{j}-\frac{\Delta t}{\Delta x}\left( \tilde{f}^{n}_{j+\frac{1}{2}}-\tilde{f}^{n}_{j-\frac{1}{2}}\right) \\
&=q^{n}_{j}-\frac{\Delta t}{2\Delta x}\left((q^{n}_{j})^2-(q^{n}_{j-1})^2\right) \\
&=q^{n}_{j}-\frac{q^{n}_{j}+q^{n}_{j-1}}{2}\frac{\Delta t}{\Delta x}\left(q^{n}_{j}-q^{n}_{j-1}\right)
\tag{16}
\end{align}
上式について非保存型での離散化式\((12)\)と比較すると移流速度の部分に差があることが分かります。非保存型(式\((12)\))では特に考えなしに右辺第二項の移流速度\(q\)を\(q^{n}_{j}\)と離散化しましたが、保存型での移流速度は風上側の節点との平均速度\(\frac{q^{n}_{j}+q^{n}_{j-1}}{2}\)として求まります。
実はこの点が極めて重要で移流速度を\(q^{n}_{j}\)の一点のみで表現してしまうと、周囲節点情報が一切反映されなので、例えば\(q\)が不連続に変化するような衝撃波部分の移流速度は正しくとられられないことが知られています。
全領域で\(q<0\)を仮定した場合、式\((15)\)の風上部分を書き換えればよいので
q^{n+1}_{j}&=q^{n}_{j}-\frac{\Delta t}{\Delta x}\left( \tilde{f}^{n}_{j+\frac{1}{2}}-\tilde{f}^{n}_{j-\frac{1}{2}}\right) \\
&=q^{n}_{j}-\frac{\Delta t}{2\Delta x}\left((q^{n}_{j+1})^2-(q^{n}_{j})^2\right) \\
&=q^{n}_{j}-\frac{q^{n}_{j+1}+q^{n}_{j}}{2}\frac{\Delta t}{\Delta x}\left(q^{n}_{j+1}-q^{n}_{j}\right)
\tag{17}
\end{align}
この場合も移流速度は風上側の節点との平均速度となります。
ここまでの結果から保存型表示の離散化では「移流速度をその両側の節点の物理量\(q\)の平均値から定め、その方向に対し風上側の点が数値流束として採用される」ことが分かります。
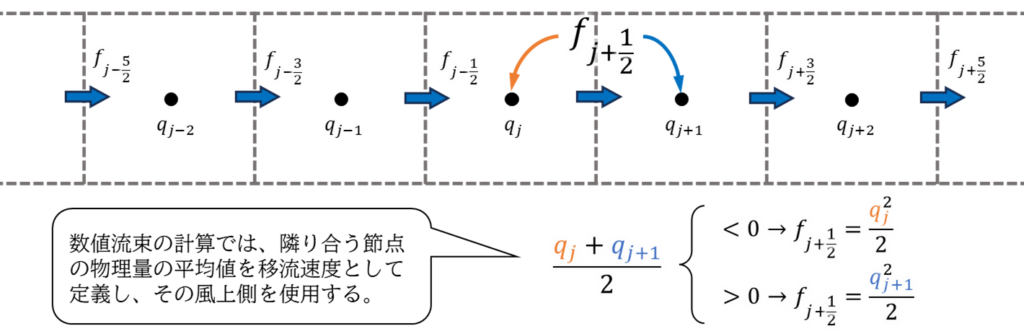
最後に非粘性Bugers方程式の1次風上差分法による数値流束の計算方法についてまとめると以下のように書けます。
&q^{n+1}_{j}=q^{n}_{j}-\frac{\Delta t}{\Delta x}\left( \tilde{f}^{n}_{j+\frac{1}{2}}-\tilde{f}^{n}_{j-\frac{1}{2}}\right) \\
\tag{18}
\end{align}
\tilde{f}^{n}_{j+\frac{1}{2}}=
\begin{cases}
\frac{(q^{n}_{j})^2}{2} & \text{$\frac{q^{n}_{j+1}+q^{n}_{j}}{2} \geq 0$のとき} \\
\frac{(q^{n}_{j+1})^2}{2} & \text{$\frac{q^{n}_{j+1}+q^{n}_{j}}{2} < 0$のとき}
\end{cases}
\tag{19}
\end{equation}\begin{equation}
\tilde{f}^{n}_{j-\frac{1}{2}}=
\begin{cases}
\frac{(q^{n}_{j-1})^2}{2} & \text{$\frac{q^{n}_{j}+q^{n}_{j-1}}{2} \geq 0$のとき} \\
\frac{(q^{n}_{j})^2}{2} & \text{$\frac{q^{n}_{j}+q^{n}_{j-1}}{2} < 0$のとき}
\end{cases}
\tag{20}
\end{equation}
さらに式\((19),(20)\)は以下のように一本の式で書くことも可能です。
\begin{equation}
\tilde{f}^{n}_{j+\frac{1}{2}}=\frac{1}{2}\left[\frac{(q_{j+1}^{n})^2}{2}+\frac{(q_{j}^{n})^2}{2}-\mathrm{sgn}\left(\frac{q^{n}_{j+1}+q^{n}_{j}}{2}\right)\left(\frac{(q_{j+1}^{n})^2}{2}-\frac{(q_{j}^{n})^2}{2}\right)\right]
\tag{21}
\end{equation}\begin{equation}
\tilde{f}^{n}_{j-\frac{1}{2}}=\frac{1}{2}\left[\frac{(q_{j}^{n})^2}{2}+\frac{(q_{j-1}^{n})^2}{2}-\mathrm{sgn}\left(\frac{q^{n}_{j}+q^{n}_{j-1}}{2}\right)\left(\frac{(q_{j}^{n})^2}{2}-\frac{(q_{j-1}^{n})^2}{2}\right)\right]
\tag{22}
\end{equation}
数値解析
次に上記の1次元非粘性Bugers方程式について非保存形・保存形で実際に解いてみます。初期値として以下の矩形波を与えることとします。
\begin{equation}
q=
\begin{cases}
1 & \text{$x \leq 1$のとき} \\
0 & \text{$x>1$のとき}
\end{cases}
\tag{23}
\end{equation}
以下に要素数7の場合の各変数の配置を示します。数値流束\(f\)と物理量\(q\)の位置関係に注意してください。

以下に解析結果のアニメーションを示します。
保存型の場合、速度0.5で波が進行するのに対して、非保存型の場合、波が停止してしまっています。これは式\((14)\)から分かるように、移流速度が\(q_{j}\)のみから定義されているため、\(q=0\)となる領域で\(q_{j}^{n+1}=q_{j}^{n}\)となり波が動かないためです。
保存型から得られる解は厳密解をある程度再現することが知られており、非線形問題においては保存型表示を用いるのが一般的です。(ただそもそも非粘性Bugers方程式の厳密解ってどうやって求めるの?という疑問もあるのですが、この辺りはいつか別記事にてまとめられればと思います。)
MATLABコード
以下に今回用いたコードを記載します。githubにもアップしましたのでよろしければご参考ください。
% 初期化
clearvars;
% パラメーター
Lx = 4;% 計算領域
dLx = 0.01;% 要素サイズ
dt = 0.005;
nx = Lx / dLx + 1;% 要素数
t_max = 3;
iter_max = t_max / dt;
% 座標の生成
x = 0 : dLx : Lx;
% 配列確保
qf = zeros(nx, 1);% 保存型表示の解
q = zeros(nx, 1);% 非保存型表示の解
flux = zeros(nx - 1, 1);
% 初期条件の設定
for i = 1 : nx
if abs(x(i) - 1) <= 10^-6
q(i) = 1;
qf(i) = 1;
elseif x(i) < 1
q(i) = 1;
qf(i) = 1;
else
q(i) = 0;
qf(i) = 0;
end
end
% 時間発展
for iter = 1 : iter_max
time = iter * dt;
q_old = q;
qf_old = qf;
% 保存型の時間発展
flux = CalcFlux(flux, qf_old, nx);% フラックスの計算
for i = 2 : nx - 1
qf(i) = qf_old(i) - (dt / dLx) * (flux(i) - flux(i - 1));
end
% 非保存型の時間発展
for i = 2 : nx - 1
q(i) = q_old(i)...
- 0.5 * (q_old(i) + abs(q_old(i))) * (dt / dLx) * (q_old(i) - q_old(i - 1))...
- 0.5 * (q_old(i) - abs(q_old(i))) * (dt / dLx) * (q_old(i + 1) - q_old(i));
end
% コマンドウィンドウへの出力
txt = ['iter = ', num2str(iter), ' / ', num2str(iter_max)];
disp(txt);
% 動画保存
if iter == 1
plotconfig(x, q, qf, time)
filename = ['nonvisco_burgers_1d','.mp4'];
v = VideoWriter(filename, 'MPEG-4');
v.FrameRate = 40;
open(v);
else
plotconfig(x, q, qf, time)
frame = getframe(gcf);
writeVideo(v,frame);
end
end
% 動画ファイルを閉じる
close(v);
function [flux] = CalcFlux(flux, q, nx)
% 保存型表示のフラックスを求める。
% flux(i)はf_{i+1/2}に相当
for i = 1 : nx - 1
ur = q(i + 1);
ul = q(i);
fr = 0.5 * ur^2;
fl = 0.5 * ul^2;
c = 0.5 * (ur + ul);
flux(i) = 0.5 * (fr + fl -sign(c) * (fr - fl));
end
end
function [] = plotconfig(x, qf, q, t)
plot(x, qf, x, q)
title(['time = ', num2str(t, '%.3f')]);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 12);
axis equal;
axis tight;
axis on;
fig=gcf;
fig.Color='white';
ylim([-0.2 1.4]);
xlabel('x')
ylabel('q')
% 凡例
legend({'non-conservative', 'conservative'},'Location','southeast','FontSize', 10)
% 新しいプロットの時、軸設定を保持したまま前のグラフィックスオブジェクトを消去
set(gca,'nextplot','replacechildren');
end
おわりに
今回は移流方程式に保存型表示を導入し、非線形問題で正しい解が得られることを確認しました。今まで数値流束のことを知らず、NS方程式なんかも解いてしまっていたので理解できてよかったです。
この後はTVD法のまとめに進もうと思ったのですが、実際学習してみるとTVD法はガッツリ有限体積法のフレームワークに基づいていて、差分法から分かりやすく理解するのは私の頭では難しいということに気づきました。ですので今後は有限体積法について学んでいければと思います。
参考文献
[1] 藤井孝蔵、立川智章、Pythonで学ぶ流体力学の数値計算法、2020/10/20



コメント