はじめに
1次元の移流方程式や拡散方程式といった偏微分方程式を離散化した際、代数方程式の係数行列として、三重対角行列(対角成分とその両隣の要素のみが非ゼロ)が得られる場合があります。この場合、代数方程式の解法としてガウスの消去法よりも効率的な三重対角行列アルゴリズム (TDMA: TriDiagonal-Matrix Algorithm) を利用することが出来ます。今回は簡単な例題を通してTDMAの基本アルゴリズムについて解説・実装を行っていきたいと思います。
直接法と反復法
連立線形方程式の数値解法は直接法と反復法に分類されます。直接法は直接消去法に基づく計算手法で、ガウスの消去法、LU分解などが含まれます。一方、反復法は初期値から収束するまで反復処理によって解を得る計算手法でガウス・ザイテル法、SOR、共役勾配法などが含まれます。今回紹介するTDMAは基本的には直接法に分類される手法です。

同様の直接法であるガウスの消去法は\(O(n^3)\)の計算量であるのに対し、TDMAは\(O(n)\)の計算量となっており、非常に効率的なアルゴリズムです。またTDMAは反復法として用いることで、係数行列が三重対角行列以外場合にも応用可能な手法です。
アルゴリズム
例として、下記のような\(n*n\)の三重対角行列を係数に持つ連立一次方程式を考えます。
&A\boldsymbol{u}=\boldsymbol{d}\\\\
&\Leftrightarrow\left(
\begin{array}{ccccccc}
b_{1} & c_{1} & \quad & \quad & \quad & \quad & \quad \\
a_{1} & b_{2} & c_{2} & \quad & \quad & \quad & \quad \\
\quad & a_{2} & b_{3} & c_{3} &\quad & \quad & \quad \\
\quad & \quad & \quad & \ddots &\quad & \quad & \quad \\
\quad & \quad & \quad & \quad &\ddots & \quad & \quad \\
\quad & \quad & \quad & \quad & a_{n-2} & b_{n-1} & c_{n-1} \\
\quad & \quad & \quad & \quad &\quad & a_{n-1} & b_{n} \\
\end{array}
\right)
\left(
\begin{array}{c}
u_{1} \\
u_{2} \\
u_{3} \\
\vdots \\
\vdots \\
u_{n-1} \\
u_{n} \\
\end{array}
\right)
=
\left(
\begin{array}{c}
d_{1} \\
d_{2} \\
d_{3} \\
\vdots \\
\vdots \\
d_{n-1} \\
d_{n} \\
\end{array}
\right)
\tag{1}
\end{align}
ここで\(A,\boldsymbol{d}\)は既知とし、未知量\(\boldsymbol{u}\)を求めるものとします。\(b,d\)はそれぞれ\(n\)個あり、\(a,c\)はそれぞれ\(n-1\)個あることに注意してください。
まず行列の1行目について抽出・変形します。
b_{1}u_{1}+c_{1}u_{2}
=
d_{1}
\Leftrightarrow
u_{1}
=
\frac{d_{1}}{b_{1}}-\frac{c_{1}}{b_{1}}u_{2}
\tag{2}
\end{align}
ここで
f_{1}=\frac{d_{1}}{b_{1}}e_{1}=\frac{c_{1}}{b_{1}}
\tag{3}
\end{align}
e_{1}=\frac{c_{1}}{b_{1}}
\tag{4}
\end{align}
と置けば、式\((2)\)は以下のように書けます。
u_{1}
=
f_{1}-e_{1}u_{2}
\tag{5}
\end{align}
上式から\(u_{1}\)を求めるためには\(u_{2}\)が必要となることが分かります。そこで次に\(u_{2}\)を求めるために、式\((1)\)の2行目を考えます。
&a_{1}u_{1}+b_{2}u_{2}+c_{2}u_{3}=d_{2}&\\\\
\Leftrightarrow
&u_{2}=\frac{d_{2}}{b_{2}}-\frac{a_{1}}{b_{2}}u_{1}-\frac{c_{2}}{b_{2}}u_{3}&
\tag{6}
\end{align}
これに式\((5)\)を代入すると、
&u_{2}=\frac{d_{2}}{b_{2}}-\frac{a_{1}}{b_{2}}(f_{1}-e_{1}u_{2})-\frac{c_{2}}{b_{2}}u_{3}&\\
\Leftrightarrow
&u_{2}=\frac{d_{2}}{b_{2}}-\frac{a_{1}}{b_{2}}f_{1}+\frac{a_{1}}{b_{2}}e_{1}u_{2}-\frac{c_{2}}{b_{2}}u_{3}&\\
\Leftrightarrow
&(1-\frac{a_{1}}{b_{2}}e_{1})u_{2}=\frac{d_{2}}{b_{2}}-\frac{a_{1}}{b_{2}}f_{1}-\frac{c_{2}}{b_{2}}u_{3}&\\
\Leftrightarrow
&u_{2}=\frac{d_{2}}{b_{2}(1-\frac{a_{1}}{b_{2}}e_{1})}-\frac{a_{1}}{b_{2}(1-\frac{a_{1}}{b_{2}}e_{1})}f_{1}-\frac{c_{2}}{b_{2}(1-\frac{a_{1}}{b_{2}}e_{1})}u_{3}&\\
\Leftrightarrow
&u_{2}=\frac{d_{2}-a_{1}f_{1}}{b_{2}-a_{1}e_{1}}-\frac{c_{2}}{b_{2}-a_{1}e_{1}}u_{3}\tag{7}&\\
\end{align}
ここで\(f_{2}=\frac{d_{2}-a_{1}f_{1}}{b_{2}-a_{1}e_{1}},e_{2}=\frac{c_{2}}{b_{2}-a_{1}e_{1}}\)とおけば
u_{2}=f_{2}-e_{2}u_{3}
\tag{8}
\end{align}
式\((8)\)は式\((5)\)と同様の形をしていることに注意します。繰り返しになりますが、次は\(u_{3}\)を求めるために、式\((1)\)の3行目を考えてみます。
a_{2}u_{2}+b_{3}u_{3}+c_{3}u_{4}=d_{3}\\\\
\Leftrightarrow
u_{3}=\frac{d_{3}}{b_{3}}-\frac{a_{2}}{b_{3}}u_{2}-\frac{c_{3}}{b_{3}}u_{4}
\tag{9}
\end{align}
式\((9)\)は式\((6)\)と同様の形をしています。したがって、これに式\((5)\)と同じ形の式\((8)\)を代入すれば、結果的に\(u_{3}\)は式\((8)\)と同じ形になり以下のように書けます。
u_{3}=f_{3}-e_{3}u_{4}
\tag{10}
\end{align}
ここで、\(f_{3}=\frac{d_{3}-a_{2}f_{2}}{b_{3}-a_{2}e_{2}},e_{3}=\frac{c_{3}}{b_{3}-a_{2}e_{2}}\)としています。
以上より、\(i=2\sim n-1\)行目で以下の式が成り立つと考えられます。
u_{i}=f_{i}-e_{i}u_{i+1}
\tag{11}
\end{align}
f_{i}=\frac{d_{i}-a_{i-1}f_{i-1}}{b_{i}-a_{i-1}e_{i-1}}
\tag{12}
\end{align}
e_{i}=\frac{c_{i}}{b_{i}-a_{i-1}e_{i-1}}
\tag{13}
\end{align}
ここまでの変形から\(u_{n}\)を求めるために\(u_{n+1}\)が必要な構造になっていることが分かります。では最終行である\(n\)行目はどうなってるでしょうか?同様に考えると
a_{n-1}u_{n-1}+b_{n}u_{n}=d_{n}
\Leftrightarrow
u_{n}=\frac{d_{n}}{b_{n}}-\frac{a_{n-1}}{b_{n}}u_{n-1}
\tag{14}
\end{align}
ここで式\((11)\)より\(i=n-1\)として
u_{n-1}=f_{n-1}-e_{n-1}u_{n}
\tag{15}
\end{align}
式\((15)\)を式\((14)\)に代入すれば、
&u_{n}=\frac{d_{n}}{b_{n}}-\frac{a_{n-1}}{b_{n}}(f_{n-1}-e_{n-1}u_{n})&\\
&\Leftrightarrow u_{n}=\frac{d_{n}}{b_{n}}-\frac{a_{n-1}}{b_{n}}f_{n-1}+\frac{a_{n-1}}{b_{n}}e_{n-1}u_{n}&\\
&\Leftrightarrow \left(1-\frac{a_{n-1}}{b_{n}}e_{n-1}\right)u_{n}=\frac{d_{n}}{b_{n}}-\frac{a_{n-1}}{b_{n}}f_{n-1}&\\
&\Leftrightarrow u_{n}=\frac{d_{n}}{b_{n}\left(1-\frac{a_{n-1}}{b_{n}}e_{n-1}\right)}-\frac{a_{n-1}}{b_{n}\left(1-\frac{a_{n-1}}{b_{n}}e_{n-1}\right)}f_{n-1}&\\
&\Leftrightarrow u_{n}=\frac{d_{n}-a_{n-1}f_{n-1}}{b_{n}-a_{n-1}e_{n-1}}&\tag{16}
\end{align}
以上より\(u_{n}\)は既知量のみから計算できることが分かります。未知量\(u_{i}\)について、ここまでの計算結果をまとめると以下のようになります。
1)\(i=1\)のとき
&u_{1}=f_{1}-e_{1}u_{2}&\tag{5}\\
&f_{1}=\frac{d_{1}}{b_{1}}\tag{3}&\\
&e_{1}=\frac{c_{1}}{b_{1}}\tag{4}&\\
\end{align}
2)\(i=2 \sim n-1\)のとき
u_{i}=f_{i}-e_{i}u_{i+1}\tag{11}\\
f_{i}=\frac{d_{i}-a_{i-1}f_{i-1}}{b_{i}-a_{i-1}e_{i-1}}\tag{12}\\
e_{i}=\frac{c_{i}}{b_{i}-a_{i-1}e_{i-1}}\tag{13}\\
\end{align}
3)\(i=n\)のとき
u_{n}=\frac{d_{n}-a_{n-1}f_{n-1}}{b_{n}-a_{n-1}e_{n-1}}\tag{16}
\end{align}
注意すべき点としては、既知量である\(f_{i},e_{i}\)は前進消去で\(i=1→n\)と求めていく必要があり、未知量である\(u_{i}\)は後退代入で\(i=n→1\)と求めていく必要がある点です。従ってアルゴリズムは下記のようになります。
| 1 | 式\((3),(4)\)より\(f_1,e_1\)を求める。 |
| 2 | 式\((12),(13)\)より\(f_i,e_i\)を\(i=2 → n-1\)の順で求める。 |
| 3 | 式\((16)\)より\(u_n\)を求める。 |
| 4 | 式\((11)\)より\(u_i\)をを\(i=n-1 →2\)の順で求める。 |
| 5 | 式\((5)\)より\(u_1\)を求める。 |
結局のところ、この方法はガウスの消去法のように前進消去、後退代入を行っていますが三重対角部分のみ計算を行うので計算量が少ないというわけです。
問題設定
次は実際に下記、連立一次方程式をTDMA法を用いてMatlabで解いてみます。
\left(
\begin{array}{ccc}
3 & 1 & 0 \\
1 & 4 & 2 \\
0 & 4 & 5 \\
\end{array}
\right)
\left(
\begin{array}{c}
u_{1} \\
u_{2} \\
u_{3} \\
\end{array}
\right)
=
\left(
\begin{array}{c}
5 \\
15 \\
9 \\
\end{array}
\right)
\tag{17}
\end{align}
解として\(\left(
\begin{array}{c}
u_{1} \\
u_{2} \\
u_{3} \\
\end{array}
\right)=
\left(
\begin{array}{c}
1 \\
2 \\
3 \\
\end{array}
\right)\)が得られれば成功です。
MATLABコード
以上を踏まえて作成したMATLABコードを以下に記載します。(こちらにもアップしています。)
% 初期化
clear all;
% Au=d
A = [3, 1, 0; 1, 4, 2; 0, 2, 5];
d = [5, 15, 19];
% 行列Aが三重対角行列か確認
Adim = size(A, 1);
n = 0;
for i = 2 : Adim - 1
Adiags_p = spdiags(A, i);% 非三重対角部分を抽出
Adiags_m = spdiags(A, -i);% 非三重対角部分を抽出
n = n + nnz(Adiags_p) + nnz(Adiags_m);% 非三重対角部分の非ゼロ要素の数を数える。
end
if n > 0
disp('行列Aは三重対角行列ではありません。計算を終了します。')
return;% スクリプト終了
end
% 成分抽出
b = spdiags(A, 0);% 対角成分の抽出
a = spdiags(A, - 1);% 三重対角成分の抽出(マイナス側)
c = spdiags(A, 1);% 三重対角成分の抽出(プラス側)
a = a(1 : end - 1);% 余計な成分を削除
c = c(2 : end);% 余計な成分を削除
% 求解
u = TDMA(a, b, c, d);
disp(u)
%% 以下関数
function[u] = TDMA(a, b, c, d)
%a,cはn-1個の要素
%b,dはn個の要素
n = size(d, 2);% 未知変数の数
e = zeros(n - 1);
f = zeros(n - 1);
% 1番目の係数を求める
e(1) = c(1) / b(1);
f(1) = d(1) / b(1);
% 2からn-1番目の係数を求める
for i = 2 : n - 1
e(i) = c(i) / (b(i) - a(i - 1) * e(i - 1));
f(i) = (d(i) - a(i - 1) * f(i - 1)) / (b(i) - a(i - 1) * e(i - 1));
end
% n番目の解を求める
u(n) = (d(n) - a(n - 1) * f(n - 1)) / (b(n) - a(n - 1) * e(n - 1));
% n-1から1番目の解を求める
for i = n - 1 : - 1 : 1
u(i) = f(i) - e(i) * u(i + 1);
end
end実行結果
実行結果は下記のとおりです。うまくいったようです。
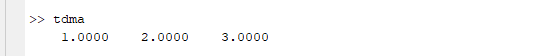
おわりに
今回は簡単な例題を通して、直接法としてのTDMAについて解説しました。次回は反復法としてのTDMAを用いて、二次元ポアソン方程式を解いてみたいと思います。


