三重対角アルゴリズム（TDMA）で2次元ポアソン方程式を解く【MATLABコード付き】

はじめに

　前回は三重対角アルゴリズム（TDMA）を直接法として利用し、連立1次方程式を解くプログラムを実装しました。しかしながら、２次元以上の偏微分方程式は係数行列が三重対角行列にはならず、前回の手法をそのまま適用することは出来ません。そこで今回は前回の手法を拡張し、TDMAを反復法として用いることで、２次元ポアソン方程式を解く方法（いわゆる線順法）について解説します。

三重対角アルゴリズム（TDMA）を実装する【MATLABコード付き】

はじめに 　１次元の移流方程式や拡散方程式といった偏微分方程式を離散化した際、代数方程式の係数行列として、三重対角行列（対角成分とその両隣の要素のみが非ゼロ）が得られる場合があります。この場合、代数方程式の解法としてガウスの消去法よりも効率...

taku-naka.site

2022.05.01

2次元ポアソン方程式の離散化

　二次元の非定常熱伝導方程式は拡散方程式として以下のように書けました。

ここで定常状態を考えると左辺は０となり、定常熱伝導方程式として以下のように書けます。

この式はいわゆるポアソン方程式の形であり、上記以外にも流体解析における圧力の方程式などで現れます。今回は上記の定常熱伝導方程式にTDMAを適用することを考えます。

まず式\((2)\)の離散化を考えます。座標系は以下の通りです。

上図は\(x\)方向を下向きにとった座標系となっていますが、これは配列の行を\(x\)方向、列を\(y\)方向と紐づけて考えるためであり実装上の都合です。式\((2)\)を中心差分法で離散化すると次のように書けます。

ここで各係数は下記のとおりです。

さらに式\((3)\)を行列形式で記述すると

以上がポアソン方程式の離散化形式となります。

TDMAの適用

　次により具体的に理解するため、下図のような4*4のセル配置でポアソン方程式を考えます。

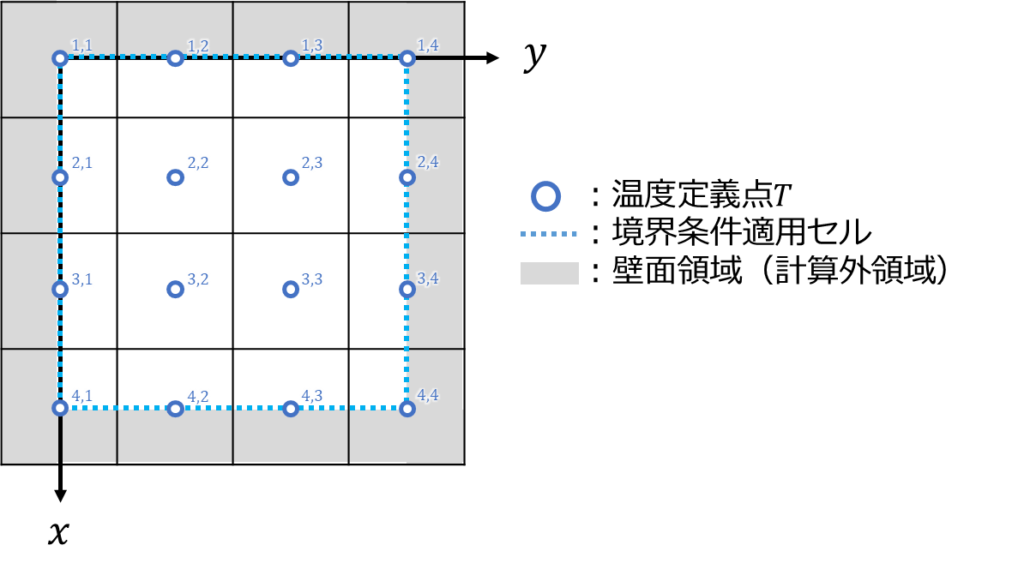
このセル配置において、式\((8)\)は以下のように書けます。

ここで\(T_{n},T_{s},T_{e},T_{w}\)は境界の温度を示しており、角部分はその平均で表しています。

式\((9)\)左辺の係数行列は対角位置より少し離れた位置に定数\(α\)を持ち、三重対角行列になっていないことが分かります。このように離散化された偏微分方程式は二次元に拡張する段階で2方向のステンシルが生じ、係数行列が三重対角行列にならないことが一般的です。このままではTDMAを利用することはできません。

そこで式\((3)\)について以下のように非三重対角成分を右辺に移項し、ソース項\(Q_{i,j}\)の一部として考えます。

前回記事で述べた通り、TDMAで解かれる方程式の基本形は以下の通りでした。

従って式\((10)\)における\(j\)を式\((11)\)における\(n\)に対応づけ、係数を以下のように見なすことで、TDMAを適用すること出来ます。

ここで右辺に移項した\(T_{i-1,j},T_{i+1,j}\)については本来は求めるべき値であり、未知数であるため、適当な初期値の下、代入を繰り返すことで解を求めます。

一般的には上記を用いて、ライン上の温度を一度に求め、それをラインに垂直な方向に領域の端から端へと走査することで、領域全体の温度を決めていく方法がとられるようです。このことから本手法は「線順法」とも呼ばれます。これに対して1点ずつ温度の反復を行う、ガウス・ザイテル法などは「点順法」と呼ばれます。

点順法は一回の反復の中で隣接４セルの温度から中心一点の温度を決めますが、線順法は隣接ラインからその間のライン上の温度を一度に決めるため、反復回数を減らすことが出来ます。（ただし、1回の反復における計算量は増加する。）

今回の場合、はじめに2行目の温度\(T_{2,j}\)をTDMAで一度に求め、それを\(i\)が大きくなる方向に走査することで、領域全体の温度を求めます。以下のスライドに7*7のセル配置の場合の計算例を記載します。ライン方向と走査方向で境界条件の与え方が若干異なること点は少し厄介かもしれません。

緩和係数による収束の加速

　上記の反復を繰り返すことでも解を得ることができますが、SOR法で行ったように解の更新時に緩和係数を乗じることで、さらに収束を加速（あるいは減速）することができます。

SOR法における緩和係数とは以下のようなものでした。

ここで\(T_{i,j}\)は次ステップの解、\(T_{i,j}^*\)は現ステップの解、\(T_{i,j}^{new}\)は反復法で得られた解、\(\omega\)は緩和係数です。上式は反復法で得られた解をそのまま次ステップの解とするのではなく、現ステップの解との差分に定数を乗じたものを現ステップの解に加算することで、一回の反復における解の修正量を大きくし、収束を早めようとしていることを意味しています。

TDMAでもこの緩和係数を取り入れることを考えます。式\((10)\)を以下のように変形します。

左辺の\(T_{i,j}\)が反復法によって得られる解なので、これを式\((13)\)の\(T_{i,j}^{new}\)に代入します。

上式と式\((11)\)を比較すると緩和係数を施したTDMAの係数は以下のように書けます。

これらの係数のもとTDMAの反復を繰り返すことで収束を加速させることができます。

問題設定

　面積\(1\rm{[m]}*1\rm{[m]}\)、熱伝導率\(1\rm{[W/m・K]}\)の領域について、定常熱伝導方程式を解きます。\(-x\)側は\(T=1\rm{[K]}\)で温度固定、\(+x\)側は\(\frac{\partial T}{\partial x}=0\rm{[K/m]}\)で断熱条件、\(\pm y\)側は\(T=0\rm{[K]}\)で温度固定とします。

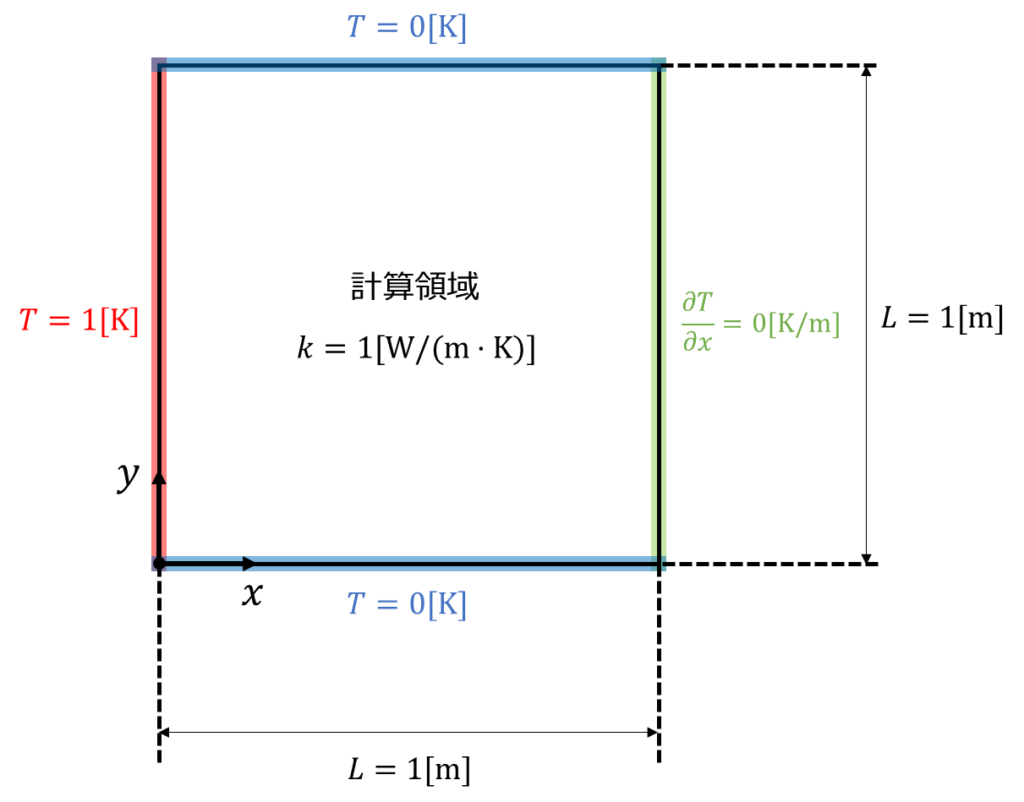
MATLABコード

　ここまでの内容を踏まえて作成したコードは以下のようになります。（こちらにもアップしています。）比較のためにSOR法も同時に実装しており、”method”でTDMAかSORのいずれかを選択することが出来ます。

% 初期化
clear all;

% パラメーター
Lx = 1;% 計算領域
Ly = 1;% 計算領域
nx = 40;% 要素数
ny = 40;% 要素数
dLx = Lx / nx;% 要素サイズ
dLy = Ly / ny;% 要素サイズ
k = 1;% 熱伝導率

% 座標の生成
x = 0 : Lx / nx : Lx;
y = Ly : - Ly / ny : 0;
[X, Y] = meshgrid(x, y);

% 配列確保
T2d = zeros(nx, ny);

% 熱源の設定
q2d = zeros(nx, ny);
%q2d(round(nx / 2), round(ny / 2)) = 1000;% 中央に単位熱源を設置する

% 時間計測開始
tic

% 連立方程式の解法を選択
method = 'TDMA';

switch method

    case 'SOR'

        T2d = SOR(T2d, q2d, k, nx, ny, dLx, dLy);

    case 'TDMA'

        alpha = 1 / (dLx)^2;
        beta = 1 / (dLy)^2;
        gamma = - 2 * (alpha + beta);
        a = zeros(1, nx - 1);
        b = zeros(nx * ny, 1);
        c = zeros(1, nx - 1);
        d = zeros(1, nx);
        T2d_new = zeros(nx, ny);

        % 反復法のパラメーター
        eps = 10^(-14);% 許容誤差
        ite_max = nx * ny *20;% 最大反復回数
        omega = 1.3;% 緩和係数

        for ite = 1 : ite_max

            error = 0;

            %ite

            for i = 2 : nx - 1

                % ±x側境界条件
                T2d(1, :) = 1;% ディリクレ条件
                T2d(end, :) = T2d(end - 1, :) ; % ノイマン条件
                %T2d(end, :) = 0; % ディリクレ条件

                % j = 1 の時 (-y側の境界条件)
                b(1) = 1;
                c(1) = 0;% ディリクレ条件
                % c(1) = -1;% ノイマン条件
                d(1) = 0;

                % j = 2 ~ ny - 1 の時(内部領域)
                for j = 2 : ny - 1
                    a(j - 1) = beta;
                    b(j) = gamma / omega;
                    c(j) = beta;
                    d(j) = - alpha * T2d(i + 1, j) - alpha * T2d(i - 1, j) - q2d(i, j) / k + (1 - omega) * gamma * T2d(i, j)/ omega;
                end

                % j = ny の時(+y側の境界条件)
                a(ny - 1) = 0;% ディリクレ条件
                % a(ny - 1) = -1;% ノイマン条件
                b(ny) = 1;
                d(ny) = 0;

                % TDMA
                T2d_new(i, :) = TDMA(a, b, c, d);

                % 誤差の計算
                for j = 2 : ny - 1
                    cor = T2d(i, j) - T2d_new(i, j);
                    error = max(error, abs(cor));
                    T2d(i, j) = T2d_new(i, j);
                end

                % 角部分は境界条件の平均とする
                T2d(1, 1) = (T2d(1, 2) + T2d(2, 1)) / 2;
                T2d(1, end) = (T2d(1, end - 1) + T2d(2, end)) / 2;
                T2d(end, 1) = (T2d(end, 2) + T2d(end - 1, 1)) / 2;
                T2d(end, end) = (T2d(end - 1, end) + T2d(end, end - 1)) / 2;

            end

            if error < eps %&& ite> 100 % 収束条件が満たされたらループを抜ける。
                break
            end

            if ite >= ite_max
                disp('最大反復回数に達しました。収束条件を満たしていません。');
            end

        end

    otherwise

        error("選択された手法：" + method + "はサポートしていないです。" + ...
            "SOR,TDMAから選択してください。");

end

% 時間計測終了
toc

% 可視化
vis_contour(T2d, x, y, Lx, Ly, 2)

%% 以下関数
function[T2d] = SOR(T2d, q2d, k, nx, ny, dLx, dLy)

% ポアソン方程式の係数定義
ac = zeros(nx, ny);
an = zeros(nx, ny);
ae = zeros(nx, ny);
as = zeros(nx, ny);
aw = zeros(nx, ny);

ac(:, :) = 2 * ((1/(dLx)^2) +(1/(dLy)^2));
an(:, :) = 1 / (dLy)^2;
ae(:, :) = 1 / (dLx)^2;
as(:, :) = 1 / (dLy)^2;
aw(:, :) = 1 / (dLx)^2;

% SOR法
eps = 10^(- 14);
ite_max = nx * ny * 20;% 反復回数
alpha = 1.7;% 緩和係数

for ite = 1 : ite_max% SOR法により圧力補正値を求める。

    %ite
    error = 0;

    for i = 1 : nx
        for j = 1 : ny

            if  i == 1% 西側境界条件
                T2d(i, j) = 1;
            elseif  i == nx% 東側境界条件
                T2d(i, j) = T2d(nx - 1, j);
            elseif  j == 1% 南側境界条件
                T2d(i, j) = 0;
            elseif  j == ny% 北側境界条件
                T2d(i, j) = 0;
            else% 内部領域
                T2d_new= ( 1 / ac(i, j) ) * ...
                    ( ae(i, j) * T2d(i + 1, j) + aw(i, j) * T2d(i - 1, j) + an(i, j)* T2d(i, j + 1) + as(i, j)* T2d(i, j - 1) + q2d(i, j)/k );
                error = max(abs(T2d_new - T2d(i, j)), error);
                T2d(i, j) = T2d(i, j) + alpha * (T2d_new - T2d(i, j));
            end
        end
    end

    if error < eps % 収束条件が満たされたらループを抜ける。
        break
    end

    if ite >= ite_max
        disp('最大反復回数に達しました。収束条件を満たしていません。');
    end

end

end

function[u] =  TDMA(a, b, c, d)

%a,cはn-1個の要素
%b,dはn個の要素

n = size(d, 2);% 未知変数の数
e = zeros(n - 1);
f = zeros(n - 1);

% 1番目の係数を求める
e(1) = c(1) / b(1);
f(1) = d(1) / b(1);

% 2からn-1番目の係数を求める
for i = 2 : n - 1
    e(i) = c(i) / (b(i) - a(i - 1) * e(i - 1));
    f(i) = (d(i) - a(i - 1) * f(i - 1)) / (b(i) - a(i - 1) * e(i - 1));
end

% n番目の解を求める
u(n) = (d(n) - a(n - 1) * f(n - 1)) / (b(n) - a(n - 1) * e(n - 1));

% n-1から1番目の解を求める
for i = n - 1 : - 1 : 1
    u(i) = f(i) - e(i) * u(i + 1);
end

end

function[] = vis_contour(T2d, x, y ,Lx, Ly, fignum)

figure(fignum);
h = imagesc(x, y, flip(T2d));
xlabel('y')
ylabel('x')
view(270, 90); % 視点の設定
xticks(0 : round(Lx / 5, 1) : Lx);
yticks(0 : round(Ly / 5, 1) : Ly);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 16);
%axis equal;
axis tight;
axis on;
pbaspect([Lx Ly 1])
colorbar;

end

実行結果

　実行結果は下記のとおりです。

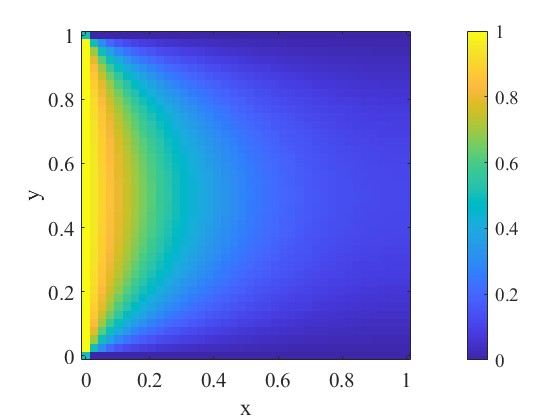
次に要素数を増やしていき、SOR法と実行時間の比較をしてみます。

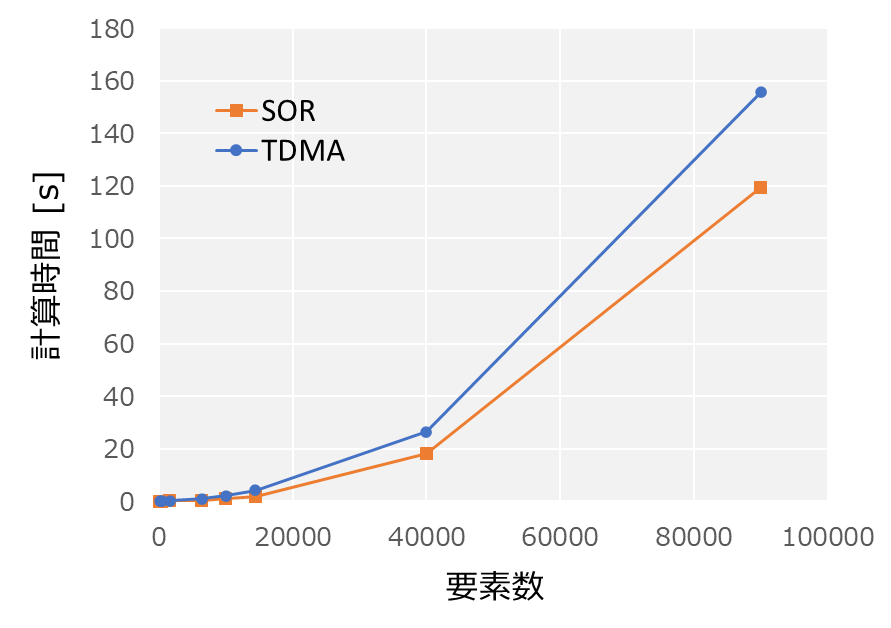
両方とも\(O(n^2)\)程度で計算できていますが、SORよりTDMAのほうが計算時間が長くなってしまいました。残念。TDMAにすることで反復回数は減っていますが、1回の反復における計算量が増加してしまったのが原因かもしれません。実装が拙い部分もあるんだろうな…。

おわりに

　今回はTDMAを用いて2次元ポアソン方程式を解いてみました。当初はSOR法よりも計算速度が速くなるかなと期待し実装してみましたが、結果的にはむしろ遅くなってしまいました。こうなると境界条件の与え方も若干複雑になるTDMAを使う理由はないですね(-_-;)共役勾配法系統のほうがいいのかな…。今後劇的に改善する見込みもないので、今回はこの辺にしておきます。修行不足！

参考文献

[1]香月 正司, 熱流動の数値シミュレーション, 2007, 森北出版