VOF法で2次元ダムブレーク問題を計算する①

はじめに

　VOF法(Volume of fluid method)は代表的な二相流解析手法の一種です。1970年代に開発されて以来、様々な改良が重ねられ、今では多くの流体解析ツールに搭載されています。しかしながら、理論的な複雑さのためか具体的な実装例を含めて解説してくれている文献はほぼないように思います。そこで今回からVOF法を用いた２次元ダムブレーク問題の実装とその解説にトライしてみます。

今回実装するスキーム

　今回は極力シンプルな手法でVOF法のエッセンスをつかむことを目指します。以下が実装するスキーム一覧です。

計算格子	スタガード格子
流速・圧力の解法	SMAC法
圧力項の離散化	中心差分法
時間の離散化	オイラー陽解法
液体体積率の移流解法	ドナー・アクセプター法

NS方程式は圧力項・重力項のみ考慮し、粘性項・表面張力は無視することとします。また液体の界面はオーバーラップしない（液体の下に気体が来ない）ものとします。

二相流の計算手法

　今回計算するダムブレーク問題は水と空気の二種の流体を扱う、いわゆる二相流の問題です。当然、二相の間では物性が異なるため生じる流速分布は違いますし、二種の流体が混ざりあったり分離したりするような複雑な界面の現象も生じます。このような複雑な現象をほんとにシミュレーションできるのか少々不安になりますが、現在に至るまで様々な解析手法が提案されているようです。以下に代表的な手法をまとめてみました。

VOF法は界面捕獲法の一種に分類され、液体の体積存在率、いわゆるVOF値の移流を計算することで気液界面を表現します。同様の界面捕獲法であるLevel Set法と比較すると原理的に体積保存性が優れているという特徴を持っています。一方で移流を計算する際に数値拡散により界面がぼやけてしまうという弱点もあります。

基礎方程式

　VOF法で用いられる基礎方程式は全部で3つあります。一つ目はナビエ・ストークス方程式です。今回は簡略化のため、移流項、粘性項および表面張力項は無視し、非定常項、圧力項、重力項のみ考えることとします。

\begin{align}
\frac{\partial }{\partial t}
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
=-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
p
+
\left(
\begin{array}{c}
0\\
g
\end{array}
\right)
\tag{1}
\end{align}

二つ目は連続の式です。非圧縮流体を仮定して速度場の発散はゼロになるものとします。

\begin{align}
\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\tag{2}
\end{align}

最後は液体体積率\(F\)の移流方程式です。\(F\)は\(0\sim 1\)の範囲を取り、上記の２式から得られた流速に基づき移流によって輸送されます。

\begin{align}
\frac{\partial F}{\partial t}+\frac{\partial (Fu)}{\partial x}+\frac{\partial (Fv)}{\partial y}=0\tag{3}
\end{align}

これら3つの方程式を時々刻々解いていくことで液体の挙動を得ることが出来ます。また、これらの方程式は以下のスタガード格子上で解くこととします。

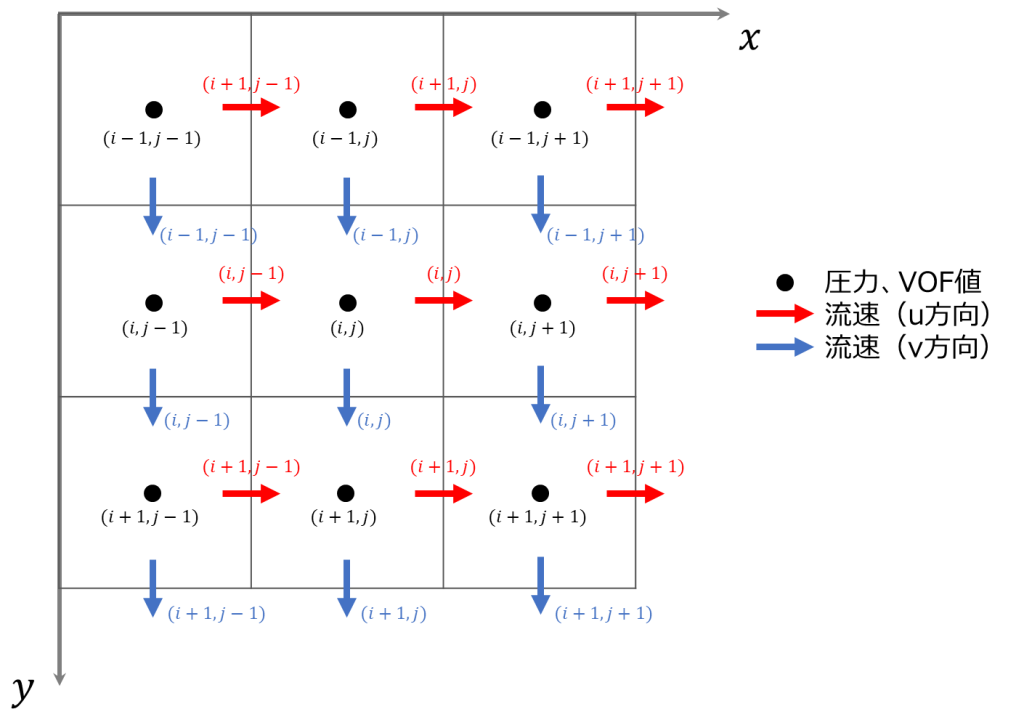
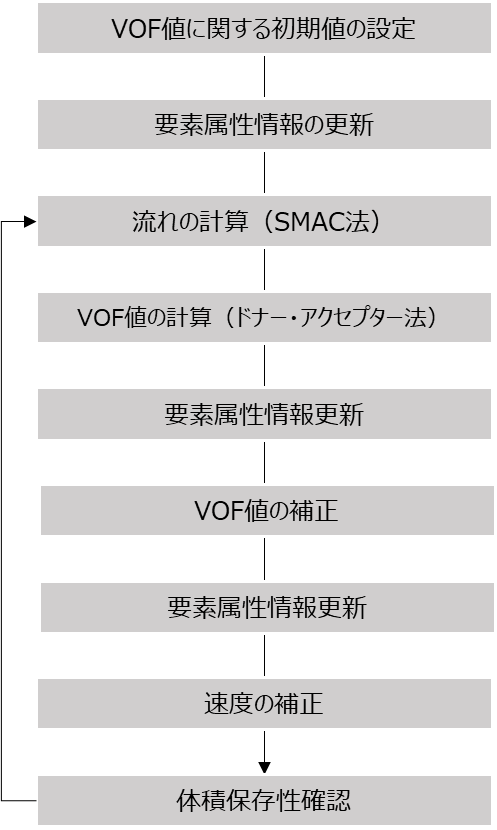
VOF法のフローチャート

　以下にVOF法のフローチャートを示します。以降は基本的にこの流れに基づき順に説明していきたいと思います。

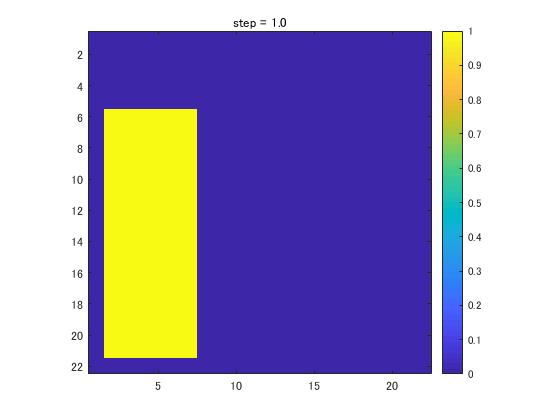
VOF値に関する初期値の設定

　まず最初にVOF値\(F\)の初期値を設定します。ダムブレークの様子を再現するため、左側に液柱領域\(F_{i,j}=1\)を設定し、それ以外の領域は気相として\(F_{i,j}=0\)としておきます。

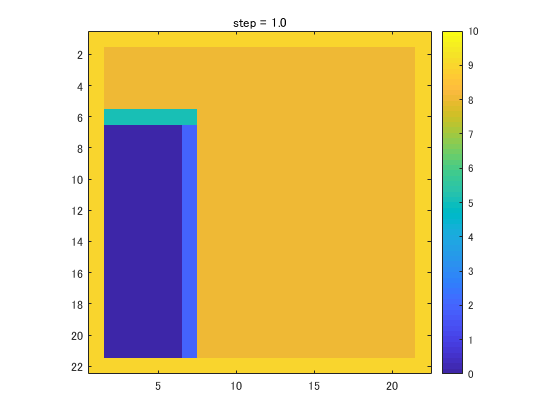
要素属性情報の更新

　VOF法では流速を計算する際、領域境界だけでなく界面にも境界条件を課します。またVOF値の移流量は界面の向きを踏まえて決める必要があります。この為、その要素が液体・気体・界面のいずれなのか（要素属性情報\(NF\)）を常に計算・更新していく必要があります。今回は以下のように設定することにします。

\(F_{i,j}\)	\(NF_{i,j}\)
内部液体	0
右液の垂直左表面	1
左液の垂直右表面	2
上表面	5
気体	8
床・天井	9

実際に\({F}\)の初期値に対して、属性情報を付与すると以下のような結果が得られます。

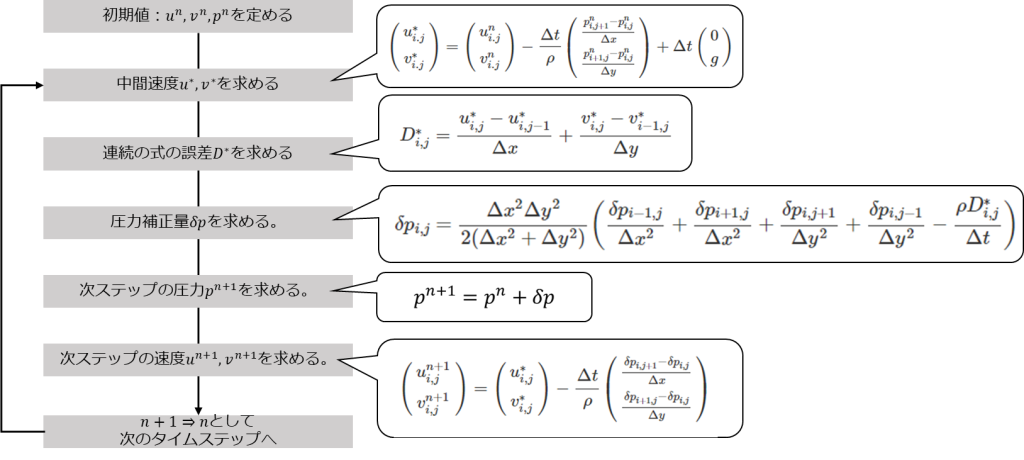
流れの計算(SMAC法)：フローチャート

　ここからしばらくはSMAC法による流れの計算について解説していきます。SMAC法に関しては以下の記事で解説を行っていますのでよろしけばご覧ください。。

今回の場合のSMAC法のフローチャートは以下のようになります。順にみていきましょう。

流れの計算(SMAC法)：初期値の設定

　SMAC法で流れの計算を行うにあたり、まずは流速\(u,v\)と圧力\(p\)の初期値を設定します。流速に関してはダム崩壊前は流れは静止しているものとして、\(t=0\)で\(u,v=0\)とすればよいでしょう。一方、圧力の初期値を得るには少々計算が必要です。

圧力は空気（液体体積率\(0\)）の圧力を基準（\(=0\)）として、液体が与える静圧のみ考えます。静圧は液体の密度を\(\rho \)とすると、水中の微小円柱要素（断面積\(S\)、高さ\(dy\)）にかかる圧力\(p(y)\)は以下のように書けました。

\begin{align}
&p(y+dy)S-p(y)S = \rho Sgdy \\
&\Leftrightarrow
p(y+dy) = p(y)+\rho gdy \tag{4}
\end{align}

上式を今回のスタガード格子上で離散化すると以下の式が得られます。

\begin{align}
p_{i,j} = p_{i-1,j}+\rho F_{i,j} gdy \
\tag{5}
\end{align}

ここでセル\((i,j)\)の密度を\(\rho F_{i,j} \)としておくことで、VOF値に応じた密度を計算するようにしています。上式は「ある液体セルの圧力はその一つ上のセルの圧力にその要素の重力分\(\rho F_{i,j} gdy\)を加算した大きさとなる」ことを示しています。

また実際の計算の際には、界面要素（右液の垂直左表、左液の垂直右表面、上表面）の圧力は０としておきます。（界面要素は一部液体なので、圧力０はおかしい様な気もしますが、逆に上式に基づいて圧力を計算してしまうと、仮の流速を求める段階で界面で圧力勾配が生じず、流速が駆動しなくなってしまうようです。）

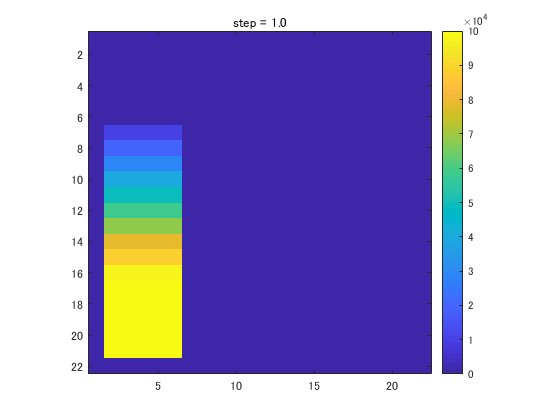
以上について実際に計算してみると\(F \)の初期値に対し、以下のような初期圧力分布が得られます。得られた分布から圧力は床に近づくほど大きくなっていることが分かります。

流れの計算(SMAC法)：仮の流速を計算

　次に設定した初期条件を用いて以下の式に基づき仮の流速を計算します。

\begin{align}
\left(
\begin{array}{c}
u^{*} \\
v^{*}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
-\frac{\Delta t}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
p^{n}
+\Delta t
\left(
\begin{array}{c}
0 \\
g\\
\end{array}
\right)
\tag{6}
\end{align}

上式はスタガード格子上で離散化すると以下のように書けます。

\begin{align}
\left(
\begin{array}{c}
u^{*}_{i.j} \\
v^{*}_{i.j}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{n}_{i.j}\\
v^{n}_{i.j}\\
\end{array}
\right)
-\frac{\Delta t}{ρ}
\left(
\begin{array}{c}
\frac{p^{n}_{i,j+1}-p^{n}_{i,j} }{\Delta x} \\
\frac{p^{n}_{i+1,j}-p^{n}_{i,j} }{\Delta y}\\
\end{array}
\right)
+\Delta t
\left(
\begin{array}{c}
0 \\
g\\
\end{array}
\right)
\tag{7}
\end{align}

仮の流速を求める際には界面に境界条件を課します。具体的には液表面があるセルは１つ液体側のセルと同じ速度になっているものとします。例えば\(u^{*}_{i,j}\)の場合、以下の図のようになります。

流れの計算(SMAC法)：連続の式の誤差を求める

　次は仮の流速\(u^*,v^*\)を用いて、連続の式の誤差\(D^*\)を求めます。

\begin{align}
D^{*}
=
\frac{\partial u^*}{\partial x}+\frac{\partial v^*}{\partial y} \tag{8}
\end{align}

上式を離散化するとセル\(i,j\)における連続の誤差\(D^{*}_{i,j}\)は以下のように書けます。

\begin{align}
D^{*}_{i,j}
=
\frac{u^*_{i,j}-u^*_{i,j-1}}{\Delta x}+\frac{v^*_{i,j}-v^*_{i-1,j}}{\Delta y} \tag{9}
\end{align}

流れの計算(SMAC法)：圧力補正量のポアソン方程式を解く

　次々行きましょう。今度は圧力補正量\(\delta p\)に関するポアソン方程式を解きます。

\begin{align}
\left(
\frac{\partial ^2 }{\partial x^2}+\frac{\partial^2 }{\partial y^2}
\right)
\delta p
=
\frac{ρD^{*}}{\Delta t}
\tag{10}
\end{align}

上式を離散化すると以下のように書けます。

\begin{align}
&\frac{\delta p_{i-1,j}-2\delta p_{i,j}+\delta p_{i+1,j}}{\Delta x^2}+\frac{\delta p_{i,j-1}-2\delta p_{i,j}+\delta p_{i,j+1}}{\Delta y^2}= \frac{ρD^{*}_{i,j}}{\Delta t}
\\
&\Leftrightarrow
\frac{1}{\Delta x^2}\delta p_{i-1,j}+\frac{1}{\Delta x^2}\delta p_{i+1,j}-2\left(\frac{1}{\Delta x^2}＋\frac{1}{\Delta y^2}\right)\delta p_{i,j}+\frac{1}{\Delta y ^2}\delta p_{i,j-1}+\frac{1}{\Delta y^2}\delta p_{i,j+1}= \frac{ρD^{*}_{i,j}}{\Delta t}\\
&\Leftrightarrow
\delta p_{i,j}= \frac{\Delta x^{2}\Delta y^{2}}{2(\Delta x^2+\Delta y^2)}\left( \frac{\delta p_{i-1,j}}{\Delta x^2}+\frac{\delta p_{i+1,j}}{\Delta x^2}+\frac{\delta p_{i,j+1}}{\Delta y^2}+\frac{\delta p_{i,j-1}}{\Delta y^2}-\frac{\rho D_{i,j}^*}{\Delta t} \right) \tag{11}\\
\end{align}

なお気体要素の場合、圧力は\(0\)とします。また圧力の境界条件としては壁面で圧力勾配０のノイマン条件を与えます。例えば床・壁面と接している左下隅の要素は上式について\(p_{i,j}=p_{i+1,j}=p_{i,j-1}\)と置くことで、以下のように計算できます。

\begin{align}
\delta p_{i,j}= \frac{\Delta x^{2}\Delta y^{2}}{\Delta x^2+\Delta y^2}\left( \frac{\delta p_{i-1,j}}{\Delta x^2}+\frac{\delta p_{i,j+1}}{\Delta y^2}-\frac{\rho D_{i,j}^*}{\Delta t} \right) \tag{12}\\
\end{align}

流れの計算(SMAC法)：次ステップの流速を求める

　最後に次ステップの流速を求めます。

\begin{align}
\left(
\begin{array}{c}
u^{n+1} \\
v^{n+1}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{*}\\
v^{*}\\
\end{array}
\right)
-\frac{\Delta t}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
\delta p
\tag{13}
\end{align}

離散化すると以下の通りです。

\begin{align}
\left(
\begin{array}{c}
u^{n+1}_{i,j} \\
v^{n+1}_{i,j} \\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{*}_{i,j} \\
v^{*}_{i,j} \\
\end{array}
\right)
-\frac{\Delta t}{ρ}
\left(
\begin{array}{c}
\frac{\delta p_{i,j+1}-\delta p_{i,j} }{\Delta x} \\
\frac{\delta p_{i+1,j}-\delta p_{i,j} }{\Delta y}\\
\end{array}
\right)
\tag{14}
\end{align}

この計算の際も、仮の流速を求めた時と同様に、界面には境界条件を課します。以上で次ステップの流れ場を決定することが出来ます。

おわりに

　長くなってきてしまったので、一度ここで記事を区切りたいと思います。今回はVOF法の流れ場を求める部分まで解説しました。次回からはVOF値の移流方程式を解く部分からまとめていく予定です。長くて息切れしそうですが、時間かけてでも完成させたい…。ではでは。