【解説】粒子の緩和時間【計算力学技術者熱流体1級（混相流）】

はじめに

　さて今回はストークス抵抗を受ける粒子の緩和時間について導出・解説していきます。粒子緩和時間についてはタイトルにある計算力学技術者認定試験熱流体1級（混相流）の2章でも問われる問題です。

粒子の緩和時間

　「粒子の緩和時間」とは粒子の速度が流れ場に馴染むまでにかかる時間のことです。数学的には流れ場中に射出された粒子の速度が\(1/e\)になるのにかかる時間を指します。粒子が重く・大きいほど、また流体の粘性が小さいほど、緩和時間は大きくなり、粒子の流れに対する追従性が悪くなります。これについて実際に流体中でストークス抵抗を受ける粒子の緩和時間（ストークス緩和時間）を導出し、確認してみましょう。

ストークス抗力は以下のように書けました。

\begin{align}F_{D}=3 \pi \mu d_{p} (v_{f}-v_{p})\tag{1} \end{align}

従って、粒子の運動方程式は以下のように書けます。

\begin{align}&m_p\frac{dv_p}{dt}=3 \pi \mu d_{p} (v_{f}-v_{p}) & \\&→ \frac{4}{3}\pi \left( \frac{d_p}{2}\right)^3 \rho_{p}\frac{dv_p}{dt}=3 \pi \mu d_{p} (v_{f}-v_{p})& \\&→ \frac{dv_p}{dt}=\frac{18 \pi \mu }{\rho_{p}d_{p}^2 }(v_{f}-v_{p})&\\&→ \frac{dv_p}{dt}=\alpha (v_{f}-v_{p})& \tag{2} \end{align}

ここで\( \alpha = \frac{18 \pi \mu }{\rho_{p}d_{p}^2 } \)と置いています。上式について変数分離型に変形して、両辺を積分すると

\begin{align}&\frac{1}{ (v_{f}-v_{p})} d(v_{f}-v_{p})\frac{dv_p}{d(v_{f}-v_{p})}=\alpha dt&\\&→ -\frac{1}{ (v_{f}-v_{p})} d(v_{f}-v_{p})=\alpha dt&\\&→ -\int \frac{1}{ (v_{f}-v_{p})} d(v_{f}-v_{p})=\alpha \int dt&\\&→ \log \left| v_{f}-v_{p}\right| = -\alpha t +C_{0} &\\& → v_{f}-v_{p}= \pm e^{-\alpha t +C_{0} }&\\&→ v_{p}= v_{f} \mp e^{-\alpha t +C_{0}}&\\&→ v_{p}= v_{f} +C_{1} e^{-\alpha t }& \tag{3} \end{align}

ここで\(C_{0},C_{1}\)は積分定数です。流速\(v_{f}\)を用いて\(t=0\)における粒子速度\(v_{p}\)の初期条件を\(v_{p}=v_{f}+v_{0}\)と与えてやると

\begin{align}& v_{f}+v_{0}= v_{f} +C_{1} & \\&→C_{1}= v_{0} & \tag{4} \end{align}

これを式\((3)\)に代入すると、粒子速度\(v_{p}\)は以下のように書けます。

\begin{align}& v_{p}= v_{f} +v_{0} e^{-\alpha t } & \tag{5} \end{align}

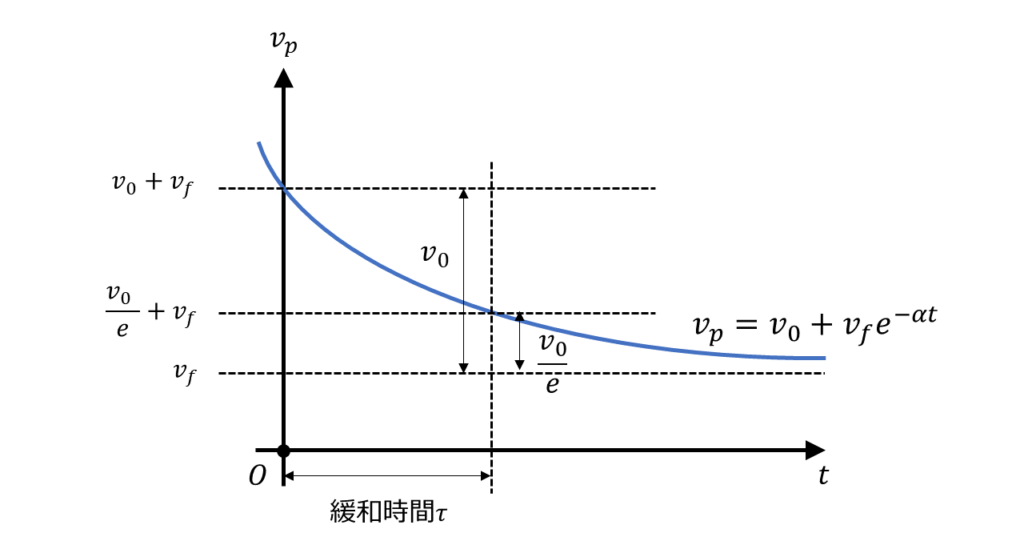
この式は制御の分野では「１次遅れ系」と呼ばれる形式です。流速\(v_{f}\)が一定であることを仮定し、これをグラフ化すると以下のようになります。

初速度\(v_{p}=v_{f}+v_{0}\)で入射された粒子は十分な時間が経過すると流速\(v_{f}\)に一致することが分かります。これは粒子速度が流速に馴染んだことを示しています。粒子の緩和時間は流れ場中に射出された粒子の速度が\(1/e\)になるのにかかる時間でした。今回の場合、\(v_{p}=\frac{v_{0}}{e}+v_{f}\)になる時間\(\tau\)を意味しています。

したがってこれらを式\((5)\)に代入すると、

\begin{align}& \frac{v_{0}}{e}+v_{f}= v_{f} +v_{0} e^{-\alpha \tau } &\\&→e^{-1}= e^{-\alpha \tau } &\\&→\tau= \alpha ^{-1} & \\&→ \tau= \frac{\rho_{p}d_{p}^2 } {18 \pi \mu } &\tag{6} \end{align}

以上がストークス緩和時間の導出になります。

以上の結果から粒子が重く・大きいほど、また流体の粘性が小さいほど緩和時間は大きくなり、粒子の流れに対する追従性が悪くなることが分かります。　

おわりに

　今回は粒子の緩和時間に関して導出・解説しました。今後、計算力学技術者試験を受ける予定のある方の少しでも役に立てれば幸いです。ではまた。