はじめに
前回までの記事で、WBMモデルによる2元合金の凝固に関する支配方程式の導出しました。今回はこれらを用いて、まずは1次元でシミュレーションを行い、解の性質について調査したいと思います。
2元系合金の凝固に関する支配方程式
WBMモデルにおいてフェーズフィールド変数の時間発展は次のアレン-カーン方程式により記述されました。
\frac{d\phi}{dt}&=
M_{\phi}
\left[
-(1-c)H^{A}(T,\phi)-cH^{B}(T,\phi)\right.\\
&\left.\quad\quad +\tilde{\epsilon} ^2
\left\{
\nabla \cdot \left(\eta^2 \nabla \phi \right)
– \frac{\partial }{\partial x}\left(\eta\frac{\partial \eta }{\partial \theta }\frac{\partial \phi }{\partial y}
\right)+
\frac{\partial }{\partial y}
\left(
\eta\frac{\partial \eta }{\partial \theta } \frac{\partial \phi }{\partial x}
\right)
\right\} \right]
\tag{1}\\
M_{\phi}&=\left(1-c\right) M^{A}+c M^{B}\tag{2}\\
H^{A}&=W^{A}\frac{\partial g}{\partial \phi}+30gL^{A} \left(\frac{1}{T}-\frac{1}{T_{m}^{A}}\right)\tag{3}\\
H^{B}&=W^{B}\frac{\partial g}{\partial \phi}+30gL^{B} \left(\frac{1}{T}-\frac{1}{T_{m}^{B}}\right)\tag{4}\\
\eta &=1+\gamma \cos\left\{k\left(\theta -\theta _0 \right) \right\} \tag{5}\\
g(\phi)&=\phi ^2\left(\phi -1\right)^2\tag{6}\\
\frac{\partial g( \phi)}{\partial \phi}&=2\phi\left(\phi -1\right) \left(2\phi -1\right)\tag{7}
\end{align}
また、濃度場の時間発展は次のカーン-ヒリアード方程式より記述されました。
\frac{dc}{dt}&=\nabla \cdot \left[D(\phi)\left\{\nabla c+\frac{v_{m}}{R}c(1-c)\left(H^B-H^A\right)\nabla \phi\right\}\right]
\tag{8}\\
D(\phi)&=D_{S}+p(\phi)(D_L-D_S)\tag{9}\\
p(\phi)&=\phi^3\left(6\phi ^2 -15\phi+10\right)\tag{10}
\end{align}
以上2種の支配方程式について解の性質を考えるため、単純な1次元系で離散化してみましょう。
アレン-カーン方程式の離散化
まずは2元合金凝固のアレン-カーン方程式\((1)\)の1次元離散化を行います。式\((1)\)を1次元化すると、右辺第三項に含まれるの界面異方性の効果は消失し、次のように書けます。
\frac{d\phi}{dt}&=
M_{\phi}
\left[
-(1-c)H^{A}(T,\phi)-cH^{B}(T,\phi)+\tilde{\epsilon} ^2 \frac{\partial ^ 2 \phi}{\partial x ^2}
\right]
\tag{11}\\
\end{align}
上式右辺に式\((2)\sim(4)\)を代入すると
\frac{d\phi}{dt}
&=\left\{\left(1-c\right) M^{A}+c M^{B}\right\}\left[-(1-c)\left\{W^{A}\frac{\partial g}{\partial \phi}+30gL^{A} \left(\frac{1}{T}-\frac{1}{T_{m}^{A}}\right)\right\}\right.\\&\left.\quad\quad\quad\quad\quad\quad\quad\quad-c\left\{W^{B}\frac{\partial g}{\partial \phi}+30gL^{B} \left(\frac{1}{T}-\frac{1}{T_{m}^{B}}\right)\right\}+\tilde{\epsilon} ^2 \frac{\partial ^ 2 \phi}{\partial x ^2} \right] \\
&=
\left\{\left(1-c\right) M^{A}+c M^{B}\right\}
\left[
-\left\{(1-c)W^{A}+cW^{B}\right\}\frac{\partial g}{\partial \phi}\right.\\
&\left.\quad\quad\quad\quad\quad\quad\quad\quad-30g\left\{(1-c)L^{A} \left(\frac{1}{T}-\frac{1}{T_{m}^{A}}\right)+cL^{B} \left(\frac{1}{T}-\frac{1}{T_{m}^{B}}\right)\right\}+\tilde{\epsilon} ^2 \frac{\partial ^ 2 \phi}{\partial x ^2}
\right] \\
&=\left\{\left(1-c\right) M^{A}+c M^{B}\right\}\left[-\left\{(1-c)W^{A}+cW^{B}\right\}\frac{\partial g}{\partial \phi}\right.\\&\left.\quad\quad\quad\quad\quad\quad\quad\quad+30g\left\{(1-c)L^{A} \left(\frac{T-T_{m}^{A}}{TT_{m}^{A}}\right)+cL^{B} \left(\frac{T-T_{m}^{B}}{TT_{m}^{B}}\right)\right\}+\tilde{\epsilon} ^2 \frac{\partial ^ 2 \phi}{\partial x ^2} \right] \tag{12}\\
\end{align}
以上が2元合金凝固における1次元アレンカーン方程式です。
次に解の性質を考えるにあたり、上式を純物質凝固における1次元アレン-カーン方程式と比較してみましょう。純物質凝固における1次元アレン-カーン方程式は次式にて与えられました。(過去記事参照)
\frac{d\phi}{dt}
&=M_{\phi}\left[-W\frac{\partial g}{\partial \phi}+30gL \left(\frac{T-T_{m}}{T_{m}}\right)+\tilde{\epsilon} ^2 \frac{\partial ^ 2 \phi}{\partial x ^2} \right] \tag{13}\\
\end{align}
パラメーターと物性値の関連付けが異なるので、潜熱項で温度の分だけ次元が異なっていますが、両者は非常に似た形であることがわかります。
まず、右辺第一項はダブルウェルポテンシャル項であり、固相・液相をより明確に分離する効果を有していました。(過去記事参照)式\((12)\)では、障壁高さ\(W\)が元素A、元素Bの濃度に応じて重みづけされており、両元素の平均的な特性が考慮されていることがわかります。
また、右辺第二項は化学的自由エネルギー密度を表しており、よりエネルギーが小さい相から大きい相の方向へ界面を移動させる効果を有していました。例えば式\((13)\)において、この項が正ならば(=温度\(T\)が融点\(T_m\)を上回っているならば)固相が液相へ変化する方向へ移動し、負であれば(=温度\(T\)が融点\(T_m\)を下回っているならば)液相が固相へ変化する方向へ移動します。
一方、式\((12)\)では、元素A、Bそれぞれの化学的自由エネルギー密度の合算で項全体の符号が決まります。例えば、温度\(T\)が元素Aの融点\(T_{m}^{A}\)より大きく、元素Bの融点\(T_{m}^{B}\)より小さいような場合、界面がどちらの方向に移動するかは、温度\(T\)がそれぞれの融点からどれだけ離れているか(\(T-T_{m}^{A},T-T_{m}^{B}\))、濃度\(c\)、潜熱\(L^{A},L^{B}\)のバランスによって決定されるわけです。
以上のように、一見複雑に見えた2元合金凝固のアレンカーン方程式もバラしてみると純物質凝固の方程式の拡張になっていることが分かります。
最後に式\((12)\)を離散化します。時間はオイラー陽解法で、空間は中心差分法で離散化します。
\frac{\phi_{i}^{n+1}-\phi_{i}^{n}}{\Delta t}
&=\left\{\left(1-c_{i}^{n}\right) M^{A}+c_{i}^{n} M^{B}\right\}\left[-\left\{(1-c_{i}^{n})W^{A}+cW^{B}\right\}\left(\frac{\partial g}{\partial \phi}\right)_{i}^{n}\right.\\
&\left.\quad\quad+30g_{i}^{n}\left\{(1-c_{i}^{n})L^{A} \left(\frac{T-T_{m}^{A}}{TT_{m}^{A}}\right)+c_{i}^{n}L^{B} \left(\frac{T-T_{m}^{B}}{TT_{m}^{B}}\right)\right\}\right.\\
&\left.\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad+\tilde{\epsilon} ^2 \frac{\phi_{i+1}^{n}-2\phi_{i}^{n}+\phi_{i-1}^{n}}{(\Delta x)^2 } \right] \tag{14}\\
g_{i}^{n}&=(\phi_{i}^{n}) ^2\left(\phi_{i}^{n} -1\right)^2\tag{15}\\
\left(\frac{\partial g}{\partial \phi}\right)_{i}^{n}&=2\phi_{i}^{n}\left(\phi_{i}^{n} -1\right) \left(2\phi_{i}^{n} -1\right)\tag{16}\\
\end{align}
ここでWBMモデルにおいて温度\(T\)は一定を仮定するため、離散化しないことに注意しましょう。
カーン-ヒリアード方程式の保存型表示
次に2元合金凝固のカーン-ヒリアード方程式\((8)\)についても同様に1次元離散化にしてみます。式\((8)\)を1次元化すると、次のように書けます。
\frac{dc}{dt}&=\frac{\partial }{\partial x} \left[D(\phi)\left\{\frac{\partial c}{\partial x} +\frac{v_{m}}{R}c(1-c)\left(H^B(T,\phi)-H^A(T,\phi)\right)\frac{\partial \phi}{\partial x} \right\}\right]
\tag{17}\\
\end{align}
本来であれば、上式を単純に差分法で離散化したいところですが、カーン-ヒリアード方程式は保存量に適用される方程式です。したがって上式は流体シミュレーションでもおなじみの「保存型表示」(過去記事参照)で離散化するのが適切でしょう。
上式の右辺鍵括弧内を流束\(f\)とみなし、保存型表示で表すと次のように書けます。
\frac{dc}{dt}&=-\frac{\partial f}{\partial x} \tag{18}\\
f&=f_{diff}+f_{int}\tag{19}\\
f_{diff}&= -D(\phi)\frac{\partial c}{\partial x}\tag{20}\\
f_{int}&=-D(\phi)\frac{v_{m}}{R}c(1-c)\left(H^B(T,\phi)-H^A(T,\phi)\right)\frac{\partial \phi}{\partial x}\\
&=D(\phi)\frac{v_{m}}{R}c(1-c)\left(H^A(T,\phi)-H^B(T,\phi)\right)\frac{\partial \phi}{\partial x}
\tag{21}
\end{align}
ここで後の説明の都合上、流束\(f\)は拡散項\(f_{diff}\)と界面項\(f_{int}\)の二つに分解しています。また、移流方程式と形式を合わせるためにあえて負号を掛けていることに注意しましょう。
上記のような保存型表示を用いると、式\((18)\)はセル界面での数値流束\(\tilde{f}^{n}_{i+\frac{1}{2}},\tilde{f}^{n}_{i-\frac{1}{2}}\)を用いて次のように離散化できます。
c^{n+1}_{i}=c^{n}_{i}-\frac{\Delta t}{\Delta x}\left( \tilde{f}^{n}_{i+\frac{1}{2}}-\tilde{f}^{n}_{i-\frac{1}{2}}\right) \tag{22}
\end{align}

数値流束は「単位時間・単位面積あたりにセル界面から出ていく物理量(この場合は濃度)の合計」を表していました。このように考えるとカーン-ヒリアード方程式の意味はより捉えやすくなります。
例えば、\(f_{diff}\)に含まれる\(\frac{\partial c}{\partial x} \)は濃度の空間勾配を表しており、これが大きいほど界面を通過する濃度(元素B)も多くなります。これは拡散項と同等の効果であり、直感的にも理解しやすいです。
一方で\(f_{int}\)は複雑な形をしており、解への影響が分かりづらくなっています。これについて順に考えていきましょう。
まず式\(f_{int}\)には\(c(c-1)\)が含まれています。これは次のような\(c=0.5\)の時、最も大きく、\(c=0,1\)で\(0\)となる上に凸な関数です。
このことは濃度の界面(\(c=0.5\)、元素Aと元素Bが同量存在する位置)に近いセル界面ほど、そこを通過する濃度(元素B)の総量が大きいことを示しています。また、元素Bが全くない状態(\(c=0\)のとき)ではそもそも移動する元素Bがありませんし、元素Bしかない状態(\(c=1\)のとき)では移動先に空きがありません。(数値流束の計算において\(c\)はセル界面の値で議論されます。セル界面の値は両隣のセルの平均として定義されるので、\(c=1\)の場合、界面両隣のセルの濃度が1であり行き先が埋まっていることに相当します。)このため、\(c=0,1\)のときは、濃度(元素B)はセル界面を通過できず\(0\)となると解釈できます。当たり前といえば当たり前ですね。
次に\(f_{int}\)中の\(\frac{\partial \phi}{\partial x}\)について考えてみます。この項は相界面\(0<\phi<1\)で値を持ち、バルク(\(\phi=0,1\))で\(0\)になります。したがって、これを乗じることで\(f_{int}\)が界面においてのみ値を持つようになり、バルクでは\(f_{diff}\)の拡散項のみが濃度変化を生じさせることとなります。要は\(f_{int}\)が相界面にのみ作用する項であることを規定しているわけです。
また、\(f_{int}\)には2つの元素のバルクのエネルギーの差分\(H^A(T,\phi)-H^B(T,\phi)\)が乗じてあります。これは元素Aのエネルギーが元素Bのエネルギーに対して大きければ大きいほど、より多くの元素Bがセル界面を正方向に通過することを示しています。逆に元素Bのエネルギーのほうが元素Aよりも大きい場合、負号が発生し、元素Bがセル界面を負の方向に通過する(=元素Aが正方向に通過する)こととなります。要はエネルギー的に高い元素は界面を通過しづらいことを示しているわけです。
さらに\(f_{int}\)の符号についても考えてみましょう。\(f_{int}\)の符号を規定するのは、\(\frac{\partial \phi}{\partial x}\)と\(H^A(T,\phi)-H^B(T,\phi)\)の二つです。この二つの符号次第で、濃度(元素B)がセル界面を正方向に通過するのか、負方向に通過するのかが決まります。それぞれを場合分けして考えてみましょう。
例えば、\(\frac{\partial \phi}{\partial x}<0\)かつ\(H^A(T,\phi)-H^B(T,\phi)>0\)であり、\(f_{int}\)が負となる場合を考えます。この時、フェーズフィールド変数の勾配は負なので、相界面は固体(\(\phi=1\))から液体(\(\phi=0\))へ変化します。一方で、バルクのエネルギーは元素Bよりも元素Aのほうが高い状態です。\(f_{int}\)の符号は負なので、元素Bは液相から固相方向へと移動していきます。つまり元素Bはエネルギーが低いため、より安定な固体状態に容易に変化出来るわけです。逆を言えば元素Aはエネルギーが高く、不安定な状態であるため、なかなか固相状態にはなれません。したがって、結果的に元素Bの濃度は界面の固相側で高くなり、液相側で低くなる状態が生じます。
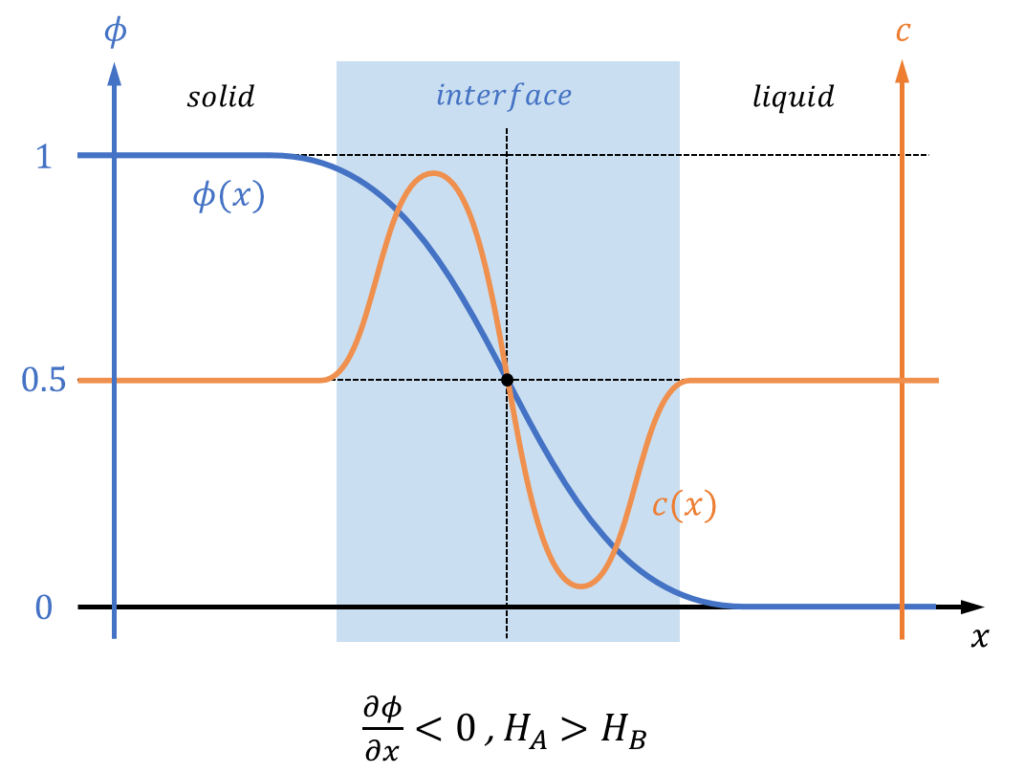
同様に\(\frac{\partial \phi}{\partial x}>0\)かつ\(H^A(T,\phi)-H^B(T,\phi)>0\)であり、\(f_{int}\)が正となる場合を考えてみます。この時、フェーズフィールド変数の勾配は正なので、相界面は液体(\(\phi=0\))から固体(\(\phi=1\))へ変化します。一方で、バルクのエネルギーは元素Bよりも元素Aのほうが高い状態です。\(f_{int}\)は符号は負なので、やはり元素Bは液相から固相方向へと移動することになります。これは界面の向きが変わっただけでは物理は変わらないことを示しています。
さらに\(\frac{\partial \phi}{\partial x}<0\)かつ\(H^A(T,\phi)-H^B(T,\phi)<0\)であり、\(f_{int}\)が正となる場合はどうでしょうか?この時、フェーズフィールド変数の勾配は負なので、相界面は固体(\(\phi=1\))から液体(\(\phi=0\))へ変化します。一方で、バルクのエネルギーは元素Aよりも元素Bのほうが高い状態です。\(f_{int}\)の符号は正なので、元素Bは固相から液相方向へと移動することになります。つまり今度は元素Bはエネルギー的に高く、不安定な状態であるため、より安定な固相状態には中々変化できないわけです。したがって、結果的に界面の液相側では元素Bの濃度が高くなり、固相側では低くなる状態が生じます。

以上をまとめると、\(f_{int}\)は「エネルギー的に高い側の元素は凝固時に固相になかなか変化できず、結果的に液相側での濃度を高め、固相側での濃度を低下させる。」という「相界面での濃度輸送現象」をモデル化していると言えます。このような物理がギブスの自由エネルギー最小化の概念から導出されるのはとても興味深いです。
カーン-ヒリアード方程式の離散化
さて、ここで数値流束\(\tilde{f}^{n}_{i+\frac{1}{2}},\tilde{f}^{n}_{i-\frac{1}{2}}\)を具体的にどのように数式として表現するかが問題です。まずは\(\tilde{f}^{n}_{i+\frac{1}{2}}\)について考えましょう。
\(\tilde{f}^{n}_{i+\frac{1}{2}}\)はセル界面\(i+\frac{1}{2}\)で定義される数値流束です。したがって、これを計算する各変数もセル界面\(i+\frac{1}{2}\)の値で考える必要があります。すなわち式\((19)\)は次のように書くことが出来ます。
\tilde{f}^{n}_{i+\frac{1}{2}}=D\left(\phi _{i+\frac{1}{2}}^{n}\right)\left\{\left(\frac{\partial c}{\partial x}\right)_{i+\frac{1}{2}} ^{n}+\frac{v_{m}}{R}c_{i+\frac{1}{2}}^{n}(1-c_{i+\frac{1}{2}}^{n})\left(H^B(T,\phi_{i+\frac{1}{2}}^{n})-H^A(T,\phi_{i+\frac{1}{2}}^{n})\right)\left(\frac{\partial \phi}{\partial x}\right)_{i+\frac{1}{2}}^{n} \right\} \tag{23}
\end{align}
ここで\(\phi _{i+\frac{1}{2}}^{n},c_{i+\frac{1}{2}}^{n}\)はセル界面\(i+\frac{1}{2}\)でのフェーズフィールド変数、濃度を表し、次のように両隣のセル中心\(i,i+1\)の値の平均として与えることとします。これは中心差分法を適用していることに相当します。
\phi^{n}_{i+\frac{1}{2}}=\frac{\phi^{n}_{i}+\phi^{n}_{i+1}}{2} \tag{24}\\
c^{n}_{i+\frac{1}{2}}=\frac{c^{n}_{i}+c^{n}_{i+1}}{2} \tag{25}
\end{align}
また、\(\left(\frac{\partial \phi}{\partial x}\right)_{i+\frac{1}{2}} ^{n},\left(\frac{\partial c}{\partial x}\right)_{i+\frac{1}{2}} ^{n}\)はセル界面\(i+\frac{1}{2}\)でのフェーズフィールド変数、濃度の空間微分を表し、両隣のセル中心\(i,i+1\)の値を用いて次のように表現されます。
\left(\frac{\partial \phi}{\partial x}\right)_{i+\frac{1}{2}} ^{n}=\frac{\phi^{n}_{i+1}-\phi^{n}_{i}}{\Delta x} \tag{26}\\
\left(\frac{\partial c}{\partial x}\right)_{i+\frac{1}{2}} ^{n}=\frac{c^{n}_{i+1}-c^{n}_{i}}{\Delta x} \tag{27}\\
\end{align}
以上、式\((24)\sim(27)\)を式\((23)\)に代入をすることで\(\tilde{f}^{n}_{i+\frac{1}{2}}\)を計算することが出来ます。実際に中身をすべて書き下したい気もしますが、プログラムコード的にもそのような表記は出てこないですし、あまり意味がないのでやめておきましょう。
同様に\(\tilde{f}^{n}_{i-\frac{1}{2}}\)は以下の通り書けます。
\tilde{f}^{n}_{i-\frac{1}{2}}&=D\left(\phi _{i-\frac{1}{2}}^{n}\right)\left\{\left(\frac{\partial c}{\partial x}\right)_{i-\frac{1}{2}} ^{n}+\frac{v_{m}}{R}c_{i-\frac{1}{2}}^{n}(1-c_{i-\frac{1}{2}}^{n})\left(H^B(T,\phi_{i-\frac{1}{2}}^{n})-H^A(T,\phi_{i-\frac{1}{2}}^{n})\right)\left(\frac{\partial \phi}{\partial x}\right)_{i-\frac{1}{2}}^{n} \right\} \tag{28}\\
\end{align}
\phi^{n}_{i-\frac{1}{2}}&=\frac{\phi^{n}_{i-1}+\phi^{n}_{i}}{2} \tag{29}\\
c^{n}_{i-\frac{1}{2}}&=\frac{c^{n}_{i-1}+c^{n}_{i}}{2} \tag{30}\\
\left(\frac{\partial \phi}{\partial x}\right)_{i-\frac{1}{2}} ^{n}&=\frac{\phi^{n}_{i}-\phi^{n}_{i-1}}{\Delta x} \tag{31}\\
\left(\frac{\partial c}{\partial x}\right)_{i-\frac{1}{2}} ^{n}&=\frac{c^{n}_{i}-c^{n}_{i-1}}{\Delta x} \tag{32}\\
\end{align}
以上の数値流束\(\tilde{f}^{n}_{i+\frac{1}{2}},\tilde{f}^{n}_{i-\frac{1}{2}}\)を式\((22)\)に代入することで濃度\(c\)の時間発展を解くことが出来ます。
解析条件
次は実際にシミュレーションしてみましょう。等温状態におけるNi-Cu合金の凝固現象を考えます。元素AをNi、元素BをCuとおき、それぞれ以下の物性値を用います。

初期条件として、空間中に一定の温度(\(T=1574\rm{[K]}\))および濃度(\(c=0.0/0.4083/0.4325/1.0\))を設定します。また、フェーズフィールド変数は領域中央に以下式で表される凝固核(\(\phi= 1\))を設定するものとします。
\phi &= \frac{1}{2}\left[1-\tanh \left(\frac{\sqrt{2W^A}}{2\epsilon}(x- x_{0})\right)\right] \tag{33}\\
\end{align}
ここで\(x_0\)は凝固領域(\(\phi=1\))の幅を表すパラメーターです。今回は相界面の観察がしやすいように、\(x_0=100dx\)と少し大きめの値を与えることとします。
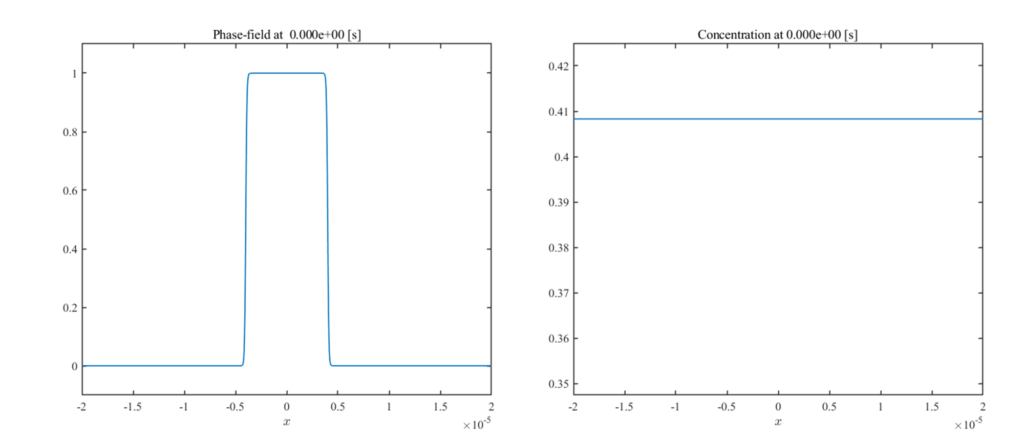
また、境界条件としては、フェーズフィールド変数・濃度ともにノイマン条件\(\frac{d\phi}{dx}=\frac{dc}{dx}=0\)を課すこととします。その他の計算パラメーターは以下の通りです。

解析ケース
解の性質を調べるため、解析ケースは以下の3ステップで行うこととします。

ステップ1では、濃度変化がフェーズフィールド変数に与える影響を検証するため、カーンヒリアード方程式は解かず、濃度は一定とします。ステップ2はカーンヒリアード方程式の各項が与える影響を調べるため、アレン-カーン方程式は解かず、バルクの数値流束\(f_{diff}\)と界面の数値流束\(f_{int}\)を段階的に適用します。最後にステップ3で全ての効果を含んだ解析を行います。
ステップ1:濃度変化がフェーズフィールド変数に与える影響の検証
まずは濃度場を\(c=0.0/0.4083/1.0\)の3ケースで固定し、フェーズフィールド変数に与える影響を調べてみます。以下に計算結果を示します。左側の縦軸がフェーズフィールド変数\(\phi\)、右側の縦軸が濃度\(c\)を表しています。
\(c=0.0\)
\(c=0.4083\)
\(c=1.0\)
まず、一番上の\(c=0.0\)の結果では、凝固核(\(\phi=1.0\))の領域が時間とともに広がっていく凝固現象が発生しています。\(c=0.0\)の場合、元素Bは全くない状態なので、系が融解するか凝固するかは元素Aの融点と系の温度の大小によってのみ決まります。元素Aの融点は\(T_{m}^A=1728\rm{[K]}\)、系の温度は\(T=1574\rm{[K]}\)なので、この場合、化学的自由エネルギーは負となり凝固が進行します。
逆に、一番下の\(c=1.0\)の結果では固核(\(\phi=1.0\))の領域が時間とともに小さくなっていく融解現象が発生しています。\(c=1.0\)の場合、元素Aは全くない状態なので、系が融解するか凝固するかは元素Bの融点と系の温度の大小によってのみ決まります。元素Bの融点は\(T_{m}^B=1358\rm{[K]}\)、系の温度は\(T=1574\rm{[K]}\)なので、この場合、化学的自由エネルギーは正となり溶融が進行します。
最後に、真ん中の\(c=0.4083\)の結果では、\(c=0.0\)と比較してゆっくりとしたスピードで凝固現象が進展していきます。これは\(c=0.0\)と\(c=1.0\)の中間の結果ともいえます。つまり、元素B(Cu)のほうが融点が低いため、濃度\(c\)(元素B(Cu)の比率)が高いほど、系としては融解しやすくなります。逆に濃度\(c\)(元素B(Ni))が小さい場合、凝固しやすくなります。
では、凝固と融解が平衡する濃度はどのように調べればよいのでしょうか?界面の移動方向を決めるのは式(14)中に含まれる以下の化学的駆動力\(\Delta g\)の項でした。
\Delta g=(1-c)L^{A} \left(\frac{T-T_{m}^{A}}{TT_{m}^{A}}\right)+cL^{B} \left(\frac{T-T_{m}^{B}}{TT_{m}^{B}}\right)\tag{34}\\
\end{align}
上式について\(T=1574\rm{[K]}\)とし、濃度\(c\)についてプロットすると以下のグラフが得られます。
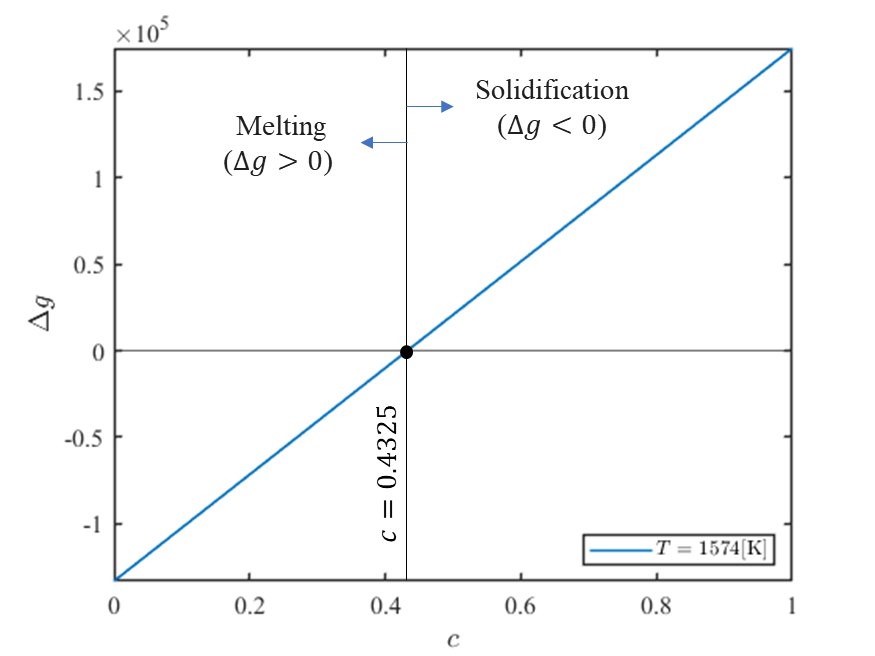
グラフより\(c=0.4325\)で\(\Delta g\)の符号が反転することが分かります。実際に\(c=0.4325\)で計算してみると、以下のように固液界面が停止し、平衡状態となります。
\(c=1.0\)
以上のように濃度変化によって融点の低い側の元素が増えれば、より融解現象が進展しやすくなり、融点の高い元素が増えれば、凝固現象が進展するようになります。
ステップ2:\(f_{diff},f_{int}\)が与える影響の検証
次にカーン-ヒリアード方程式に現れる2種の数値流束\(f_{int},f_{diff}\)(式\((19)\sim(21)\))がそれぞれどのような効果を持つか検証します。なおここではフェーズフィールド変数\(\phi\)は解かずに、初期条件で固定したままにすることとします。
まず\(f_{diff}=0\)とし、\(f_{int}\)のみ考慮した場合、次のような計算結果が得られます。
\(f_{diff}未考慮(領域全体)\)
なにやら固液界面で濃度変化が生じていることが分かります。さらに右側界面を拡大した結果を次に示します。
\(f_{diff}未考慮(右界面拡大)\)
初期段階では、前述した「界面液体側の濃度が増加し、固体側の濃度が低下する様子」が確認できます。しかしながら、時間とともに波形が不安定化し、やがて濃度が0~1の間を超えてオーバーシュートしてしまいました。確かに\(f_{int}\)は界面の濃度輸送らしきものを模擬しているようですが、この項だけだと数値的な不安定性を招くようです。
では次に\(f_{diff}\)も考慮して計算した結果を以下に示します。
\(f_{diff}考慮(領域全体)\)
\(f_{diff}考慮(右界面拡大)\)
界面液体側の濃度が増加し、固体側の濃度が低下する様子が確認できます。\(f_{diff}\)を未考慮の時と比べると、界面における濃度の波形が明らかに安定化しています。これは\(f_{diff}\)の拡散が\(f_{int}\)の鋭い波形を訛らせて数値的に安定させるためと考えられます。
また、液相側では高まった濃度は時間とともに拡散していきますが、固相側では拡散がほぼ進展しない様子が確認できます。これは固体より液体の拡散係数のほうがはるかに大きいためです。
以上より、界面濃度輸送の物理モデルは\(f_{int}\)が元素ごとのエネルギーに応じて界面における濃度の偏りを発生させ、それを\(f_{diff}\)の拡散現象によって安定化させるものであるということが分かりました。
ステップ3:すべての効果を考慮した検証
ここまでの解析では、方程式の一部の効果のみ考慮した解析を行ってきましたが、最後に全ての効果を考慮した解析を行います。初期濃度場は\(c=0.4083\)としフェーズフィールド変数も濃度場も両方解くこととします。以下に計算結果を示します。
\(すべての効果を考慮した解析結果\)
凝固が進展し、界面の液相側には高濃度領域、固相側には低濃度領域が見られます。また、時間とともに、高濃度領域が界面前方に拡散していき、これに伴い、凝固のスピードが次第に減速しています。これは元素B(Cu)の融点\(T_{m}^B=1358\rm{[K]}\)が、系の温度\(T=1574\rm{[K]}\)に対して低いため、元素Bが高い領域が広がることで、凝固しづらくなる(=融解しやすくなる)ことを示しています。
全体的な分布の形を見ると、領域中央に濃度が高い固相領域が発生しています。これは初期段階で界面に触れていないため、\(f_{int}\)の影響を受けず、なおかつ固相の拡散係数が極端に小さいため、\(f_{diff}\)の影響も受けずに残留した凝固核領域です。
さらに、濃度変化の最大・最小値を調べると、これらは\(T=1574\rm{[K]}\)における液相線濃度(\(c_{L}=0.46621\))および固相線濃度(\(c_{S}=0.3991\))に近い値となります。これは状態図上の液相線と固相線のギャップに相当しています。

このように状態図だけだと、「異相平衡領域においては液相と固相が同時に現れる」程度しか分かりませんが、フェーズフィールド法で場として解くとその分布が分かるため、より現象の理解を深めることが出来ます。
MATLABコード
以下に今回用いたMATLABコードを記載します。
%% 初期化処理
clc; close all;
clear all;
% パラメータの設定
nx = 1000; % 差分格子点数
nsteps = 5000;
dt = 3.0e-7;
dx = 4.0e-8;
pi = 3.141592;
lheat_A = 2.350e+9; % Niの潜熱 [J/m3]
lheat_B = 1.728e+9;
Tm_A = 1728.0; % Niの融点 [K]
Tm_B = 1358.0;
gamma_A = 0.37; % 界面エネルギー [J/m2]
gamma_B = 0.29;
kinetic_A = 0.0033; % 動的係数 [m/K/s]
kinetic_B = 0.0039;
D_L = 1.0e-9; % 液相での拡散係数 [m2/s]
D_S = 1.0e-13;
vmol = 7.4e-6;
rgas = 8.31451;
mag_noise = 0.1; % ノイズの大きさ
init_con = 0.4038; % 液相の初期濃度
init_temp = 1574.0; % 初期温度 [K]
delta = 6.0 * dx; % 界面の厚さ [m]
lamda = 0.1;
bbb = 2.0 * log((1.0 + (1.0 - 2.0 * lamda)) / (1.0 - (1.0 - 2.0 * lamda))) / 2.0;
tinb = gamma_A / gamma_B * Tm_B / Tm_A * delta;
eps = sqrt(3.0 * delta * gamma_A / (bbb * Tm_A)); % 勾配エネルギー係数
W_A = 6.0 * gamma_A * bbb / (delta * Tm_A); % 二重井戸ポテンシャルの高さ
W_B = 6.0 * gamma_B * bbb / (tinb * Tm_B);
M_A = bbb * Tm_A * Tm_A * kinetic_A / (3.0 * delta * lheat_A); % フェーズフィールドのモビリティ
M_B = bbb * Tm_B * Tm_B * kinetic_B / (3.0 * tinb * lheat_B);
% 配列の初期化
p_t = zeros(nx,1);
p_tdt = zeros(nx,1);
c_t = zeros(nx,1);
c_tdt = zeros(nx,1);
dpx = zeros(2, nx);
dcx = zeros(2, nx);
% 初期条件の設定
r0 = 100 * dx;
for i = 1:nx
c_t(i) = init_con;
p_t(i) = 0.0;
x(i) = dx * (i - nx / 2);
r = sqrt(x(i)^2);
p_t(i) = 0.5 * (1.0 - tanh(sqrt(2.0 * W_A) / (2.0 * eps) * (r - r0)));
if p_t(i) <= 1.0e-5
p_t(i) = 0.0;
end
end
% 時間発展
for nstep = 1 : nsteps
nstep
dpx = calc_gradient(p_t, dpx, nx, dx);
p_tdt = solve_allen_cahn(p_t, c_t, dpx, p_tdt, nx, dt, eps, W_A, W_B, lheat_A, lheat_B, init_temp, Tm_A, Tm_B, M_A, M_B, mag_noise,dx);
dcx = calc_gradient(c_t, dcx, nx, dx);
c_tdt = solve_cahn_hilliard(p_t, c_t, dpx, dcx,c_tdt, nx, dt, dx, D_L, D_S, vmol, rgas, W_A, W_B, lheat_A, lheat_B, init_temp, Tm_A, Tm_B);
p_t = p_tdt;
c_t = c_tdt;
% 保存
p_tData(:,nstep) = p_t;
c_tData(:,nstep) = c_t;
end
% 全濃度データの最大値と最小値を求める
maxp_t = max(p_tData(:))+abs(max(p_tData(:)))*0.1;
minp_t = min(p_tData(:))-0.1;
maxp_c = max(c_tData(:))+abs(max(c_tData(:)))*0.01;
minp_c = min(c_tData(:))-abs(min(c_tData(:)))*0.01;
%% 可視化
% VideoWriter オブジェクトの初期化
outputVideo = VideoWriter('phi_animation.mp4', 'MPEG-4');
outputVideo.FrameRate = 30; % フレームレートの設定
open(outputVideo);
% 複数プロット--------------------------------------------------------------
% グラフィックオブジェクトの初期化
% figure(1);
% set(gcf, 'Position', [100, 100, 1200, 600], 'Color', 'white');
% ax1 = axes('Position', [0.05, 0.1, 0.425, 0.8]);
% ax2 = axes('Position', [0.525, 0.1, 0.425, 0.8]);
% for nstep = 1 : nsteps
% nstep
% %c_tData(:,1)=0.4083;
% if mod(nstep, 20) == 0
% % Phase-field サブプロット
% axes(ax1); % 既存のaxesを指定
% cla(ax1); % 前のプロットをクリア
% plot(x, p_tData(:,nstep), 'LineWidth', 1.2);
% title(ax1, sprintf('Phase-field at %.3e [s]', (nstep - 1) * dt));
% xlabel('$$x$$', 'Interpreter', 'latex', 'FontSize', 14);
% ylim(ax1, [minp_t, maxp_t]); % Y軸の範囲を設定
% set(ax1, 'FontName', 'Times New Roman', 'FontSize', 12, 'LineWidth', 1.2);
%
% % concentration サブプロット
% axes(ax2); % 既存のaxesを指定
% cla(ax2); % 前のプロットをクリア
% plot(x, c_tData(:,nstep), 'LineWidth', 1.2);
% title(ax2, sprintf('Concentration at %.3e [s]', (nstep - 1) * dt));
% xlabel('$$x$$', 'Interpreter', 'latex', 'FontSize', 14);
% ylim(ax2, [minp_c, maxp_c]); % Y軸の範囲を設定
% set(ax2, 'FontName', 'Times New Roman', 'FontSize', 12, 'LineWidth', 1.2);
%
% frame = getframe(gcf);
% writeVideo(outputVideo, frame);
%
% end
% end
% 同一プロット--------------------------------------------------------------
% グラフィックオブジェクトの初期化
figure(1);
set(gcf, 'Position', [0, 0, 600, 400], 'Color', 'white');
for nstep = 1 : nsteps
nstep
if mod(nstep, 10) == 0
% グラフのプロット
clf; % 前のプロットをクリア
ax = axes; % 新しいaxesを作成
yyaxis left;
plot(x, p_tData(:,nstep), 'LineWidth', 1.2);
ylabel('Phase-field');
ylim([minp_t, maxp_t]); % Y軸の範囲を設定
%xlim([0.3e-5, 5e-6]); % Y軸の範囲を設定
yyaxis right;
plot(x, c_tData(:,nstep), 'LineWidth', 1.2);
ylabel('Concentration');
ylim([minp_c, maxp_c]); % Y軸の範囲を設定
%yline([0.46621 0.39911],'-',{'$$c_{L}=0.46621$$','$$c_{S}=0.39911$$'}, 'Interpreter', 'latex', 'FontSize', 10)
title(sprintf('time %.3e [s]', nstep * dt ));
xlabel('$$x$$', 'Interpreter', 'latex', 'FontSize', 14);
% TightInsetを使用して軸の位置を調整
tightInset = get(ax, 'TightInset');
left = tightInset(1) + 0.05;
bottom = tightInset(2) + 0.05;
ax_width = 0.9 - tightInset(1) - tightInset(3);
ax_height = 0.9 - tightInset(2) - tightInset(4);
set(ax, 'Position', [left, bottom, ax_width, ax_height]);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 12, 'LineWidth', 1.2);
frame = getframe(gcf);
writeVideo(outputVideo, frame);
end
end
% 動画の書き出しを完了
close(outputVideo);
%% 以下ローカル関数
function [dox] = calc_gradient(o_t, dox, nx, dx)
for i = 1:nx
ip = i + 1;
im = i - 1;
if ip > nx
ip = nx;
end
if im < 1
im = 1;
end
dox(1,i) = (o_t(ip) - o_t(i)) / dx;
dox(2,i) = (o_t(i) - o_t(im)) / dx;
end
end
function p_tdt = solve_allen_cahn(p_t, c_t, dpx, p_tdt, nx, dt, eps, W_A, W_B, lheat_A, lheat_B, init_temp, Tm_A, Tm_B, M_A, M_B, mag_noise,dx)
for i = 1:nx
phi = p_t(i);
con = c_t(i);
q_phi = phi * phi * (1.0 - phi) * (1.0 - phi);
dq_phi = 30.0 * q_phi;
ddouble_A = W_A * 2.0 * phi * (1.0 - phi) * (1.0 - 2.0 * phi);
ddouble_B = W_B * 2.0 * phi * (1.0 - phi) * (1.0 - 2.0 * phi);
H_A = ddouble_A + dq_phi * lheat_A * (init_temp - Tm_A) / (init_temp * Tm_A);
H_B = ddouble_B + dq_phi * lheat_B * (init_temp - Tm_B) / (init_temp * Tm_B);
epss = zeros(2, 1);
for k = 1:2
epss(k) = eps ;
end
eppx1 = epss(1) * epss(1) * dpx(1, i);
eppx2 = epss(2) * epss(2) * dpx(2, i);
ag = 0;%mag_noise * rand(1);
mobi = (1 - con) * M_A + con * M_B;
dpt = mobi * ((eppx1 - eppx2) / dx - (1 - 16 * ag * q_phi) * ((1 - con) * H_A + con * H_B));
%p_tdt(i) = phi;%フェーズフィールド変数を固定する場合
p_tdt(i) = phi + dpt * dt;
if p_tdt(i) <= 1.0e-20
p_tdt(i) = 0;
end
end
end
function c_tdt = solve_cahn_hilliard(p_t, c_t, dpx, dcx,c_tdt, nx, dt, dx, D_L, D_S, vmol, rgas, W_A, W_B, lheat_A, lheat_B, init_temp, Tm_A, Tm_B)
for i = 1:nx
ip = i + 1;
im = i - 1;
if ip > nx
ip = nx;
end
if im < 1
im = 1;
end
Dp = zeros(2,1);
Dc = zeros(2,1);
for k = 1:2
if k == 1
pij = (p_t(ip) + p_t(i)) / 2.0;
cij = (c_t(ip) + c_t(i)) / 2.0;
elseif k == 2
pij = (p_t(im) + p_t(i)) / 2.0;
cij = (c_t(im) + c_t(i)) / 2.0;
end
p_phi = pij^3 * (10 - 15*pij + 6*pij^2);
q_phi = pij^2 * (1 - pij)^2;
dq_phi = 30 * q_phi;
ddouble_A = W_A * 2 * pij * (1 - pij) * (1 - 2 * pij);
ddouble_B = W_B * 2 * pij * (1 - pij) * (1 - 2 * pij);
H_A = ddouble_A + dq_phi * lheat_A * (init_temp - Tm_A) / (init_temp * Tm_A);
H_B = ddouble_B + dq_phi * lheat_B * (init_temp - Tm_B) / (init_temp * Tm_B);
Dc(k) = D_L + p_phi * (D_S - D_L);
Dp(k) = Dc(k) * cij * (1 - cij) * vmol / rgas * (H_A - H_B);% 5.36
end
dca1 = Dp(1) * dpx(1,i) - Dc(1) * dcx(1,i);
dca2 = Dp(2) * dpx(2,i) - Dc(2) * dcx(2,i);
%dca1 = Dp(1) * dpx(1,i) ;% 界面項の影響だけ考慮する場合
%dca2 = Dp(2) * dpx(2,i) ;% 界面項の影響だけ考慮する場合
dcc = -((dca1 - dca2) / dx);
%dcc = 0;% 濃度変化を解かない場合
c_tdt(i) = c_t(i) + dcc * dt;
end
endおわりに
今回は1次元2元合金凝固モデル(WBMモデル)について、実際にシミュレーションしてみました。一つ一つ性質を確認してるうちに長文記事になってしまいましたが、おかげである程度の理解が得られたと思います。2元合金凝固モデルは状態図を内包した場の時間発展を記述可能である点で、驚くべき情報量と拡張性を有しています。また、このような支配方程式が自由エネルギー最小化という共通の考え方より導出されるのはとても興味深いです。この辺りがフェーズフィールド法の魅力の一つなのでしょう。次回は2次元モデルに拡張してシミュレーションしてみたいと思います。
参考文献
[1] 高木 知弘ら, “フェーズフィールド法”, 養賢堂, 2012/3/2
[2] 山中 晃徳ら, “Pythonによるフェーズフィールド法入門 基礎理論からデータ同化の実装まで”, 丸善出版, 2023/12/15
[3] 小山 敏幸ら, “フェーズフィールド法入門 (計算力学レクチャーコース) “, 丸善出版, 2013/4/13
[4] J.A. Warren, W.J. Boettinger : “Prediction of dendritic growth and microsegregation patterns in a binary alloy using the phase-field method”. Acta Metallurgica et Materialia, Volume 43, Issue 2, February 1995, Pages 689-703
[5] S.-L. Wang, R.F. Sekerka : “Thermodynamically-consistent phase-field models for solidification”. Physica D: Nonlinear Phenomena, Volume 69, Issues 1-2, 15 November 1993, Pages 189-200



コメント