有限体積法の基礎：高解像度スキーム【MATLABコード付き】

はじめに

　ここまでの記事では線形スキームと呼ばれる様々な手法で移流方程式を解いてきました。これらの手法は低コストである程度、解析解を再現可能であるものの、数値粘性や数値振動を引き起こすという問題を抱えていました。このような問題は衝撃波を扱う解析では特に精度の悪化をもたらします。そこでさらなる改善のため、今回は高解像度スキームと呼ばれる手法についてまとめていきたいと思います。

有限体積法の基礎：時間高次精度化【MATLABコード付き】

はじめに 　前回記事では多項式近似により、以下の空間高次精度化された界面物理量\({}^L\! q_{i+\frac{1}{2}},{}^R\! q_{i+\frac{1}{2}}\)を得ました。 \begin{align}{}^L\! q...

taku-naka.site

2023.08.30

移流スキームの分類

　ここまでの記事で取り上げてきた手法は、線形移流方程式に従う物理量（のセル平均値）\(\bar{\cal{q}}\)の時間発展\(\bar{\cal{q}}_{i}^{n+1}\)を以下のように\(\bar{\cal{q}}_{i}^{n}\)の線形結合として一般化することが出来ました。

　ここで\(C_{s}\)は\(\bar{\cal{q}}_{i}^{n}\)に依存しない係数です。

　例えば１次精度風上差分法の場合、以下のように書けました。(過去記事参照)

　また、Lax-Wendroff法は次のように書けました。(過去記事参照)

　以上、式\((2),(3)\)はいずれも式\((1)\)の形になっています。このような解法は線形スキームと呼ばれます。線形スキームは１次精度の場合は数値粘性を、2次精度以上の場合は数値振動を引き起こしてしまう問題がありました。ゴルドフの定理というやつです。

　ではこのような問題に対応するにはどうすればよいのでしょうか？単純に考えれば不連続領域においては１次精度風上差分にして数値振動を防ぎ、連続領域においては2次以上の高次精度解法に切り替わるようなスキームがあると理想的でしょう。

　このように解の状況に応じてスキームを切り替える手法は非線形スキームと呼ばれています。中でも次に述べるTVDの性質に基づく解法を高解像度スキームと呼び、衝撃波の実用的解析手法として広く活用されています。

全変動

　そもそも安定的に解けるスキームとはどういった性質を持つのでしょうか？これを考えるため、唐突ですが次のような量\(TV\)を考えます。

　上式はセル平均値\(\bar{q}\)について隣接セル間で差分をとり、すべてのメッシュセルで和を取っています。このことは\(\bar{q}\)のプロファイルが凸凹してるほど（＝振動的であるほど）\(TV\)の値が大きくなることを意味しています。

　さらに、次式のように\(TV\)が時間とともに減少していくという条件を課す場合、\(\bar{q}\)のプロファイルが振動・発散することなく凹凸がなだらかになっていくことを意味します。この時、\(\bar{q}\)は安定的な解であるといってよいでしょう。

　このような解を導く数値解法をTVD（Total variation diminishing：全変動減少）法と呼びます。

Hartenの定理

　では式\((5)\)を満たすスキームを具体的に考えていきます。まず天下りではありますが、TVD法が満たすべき条件を規定するHartenの定理を以下に示します。

　さて…初見だと唐突すぎてよくわかりませんが、どうやらTVDの性質（式\((a4)\)）を満たすには式\((a2),(a3)\)を満たす必要があるようです。ただ、それを考えるにしてもまず移流方程式を半離散化式にして、\(C_{i+\frac{1}{2}}^{-},C_{i-\frac{1}{2}}^{+}\)の具体的な形を導いておく必要があります。地道に計算してこれらを求めてみましょう。

　1次元線形移流方程式は有限体積法により空間に関する半離散化を施すと、次のように書けます。（過去記事参照）

　ここで線形移流方程式における流束\(f\)は移流速度\(a\)を用いて以下のように書けることに注意します。

　式\((6)\)の数値流束\(\tilde{f}_{i+\frac{1}{2}},\tilde{f}_{i-\frac{1}{2}}\)の計算には、Roeリーマンソルバ(過去記事参照)を用います。まず\(\tilde{f}_{i+\frac{1}{2}}\)について計算しましょう。

　ここで\(a^{+}=\frac{1}{2}\left(a+\left|a\right|\right),a^{-}=\frac{1}{2}\left(a-\left|a\right|\right)\)と置いています。

　同様に\(\tilde{f}_{i-\frac{1}{2}}\)は次のように書けます。

　以上、式\((8),(9)\)を式\((6)\)へ代入すると

　ここでセル界面\(i-\frac{1}{2},i+\frac{1}{2}\)における空間高次精度の界面物理量は以下のように書けました。（過去記事参照）

　これらを式\((10)\)に代入して整理すると最終的に次式が得られます。

　以上が線形移流方程式の半離散化形式です。これを用いて実際にいくつかのスキームでHartenの定理を満たすのか確認してみましょう。

　まず1次風上差分法（\(\epsilon=0\)）について考えます。この時、式\((15)\)は次のように単純化できます。

　上式と式\((a1)\)を比較すると、次式が得られます。

　上式より\(C_{i+\frac{1}{2}}^{-},C_{i-\frac{1}{2}}^{+}\)は\(a\)の符号によって値が変化するため、場合分けして考えます。

　\(a \geq 0\)の場合、

となり、式\((a2),(a3)\)を満たしています。

　また\(a \leq 0\)の場合、

となり、この場合も式\((a2),(a3)\)を満たしています。以上より1次風上差分法（\(\epsilon=0\)）はTVDの性質を満たしており、安定な解法であることが確認できました。

　次にBeam-Warming法（\(\epsilon=1,\kappa = -1\)）がHartenの定理を満たすのか考えてみましょう。式\((15)\)に\(\kappa = -1\)を代入すると

　上式について式\((a1)\)と比較すると、\(C_{i+\frac{1}{2}}^{-},C_{i-\frac{1}{2}}^{+}\)は次のように表すことが出来ます。

　ここで\(a \geq 0\)の場合、

　この時、式\((26)\)は式\((a2)\)を満たしますが、式\((27)\)が式\((a3)\)を満たすかは、右辺括弧内の符号次第です。\(a \leq 0\)の場合も同様の形になります。したがって、Beam-Warming法（\(\epsilon=1,\kappa = -1\)）は常にTVDの性質を満たす安定なスキームではないことが分かります。

　以上より、1次風上差分はTVD法ですが、空間2次精度であるBeam-Warming法はTVD法ではないことが分かりました。これらの結果はゴルドフの定理と一致しています。

勾配リミタ関数

　Hartenの定理より、1次風上差分はTVD性を有しますが、Beam-Warming法のような空間2次精度以上のスキームはTVD性を有しないことが分かりました。このことは高次精度スキームは過剰な空間補正量を加えることで、逆に不安定性を引き起こしてしまっているとも言えます。

　そこで次のように界面物理量\({}^R\! q_{i-\frac{1}{2}},{}^L\! q_{i+\frac{1}{2}}\)（式\((12),(13)\)）の高次精度項について、ある関数\(\mathit{\Phi}(r)\)をかけることで、その大きさを調整することを考えます。

　\(r\)の意味や\(\mathit{\Phi}(r)\)の具体的な形はひとまず置いておきましょう。また、「なんで右辺二項目の\(\mathit{\Phi}\)は\({}^R\! r_{i-\frac{1}{2}}\)の関数で、三項目は\({}^L\! r_{i+\frac{1}{2}}\)の関数なのか？」という疑問も湧いてきますが、それについても後で考えます。

　上式は勾配計算を調整するイメージを強調するため、次のように勾配計算を明示する形で書くと理解しやすいかもしれません。

　\(0<\mathit{\Phi}(r)<1\)の場合、高次補正量は抑制され、\(\mathit{\Phi}(r)=0\)の場合、1次精度になります。このような高次補正量の勾配を制限する関数\(\mathit{\Phi}(r)\)は勾配リミタ（slope limiter）関数と呼ばれ、様々な形が提案されています。

隣接セルの勾配比\(r\)

　さて、\(\mathit{\Phi}(r)\)の具体的な形も気になりますが、これを述べる前に変数\(r\)の正体についてはっきりさせておく必要があります。そもそもTVD法とは、冒頭に述べた通り、解の連続性・不連続性によって空間精度を切り替える手法でした。したがって、\(r\)は「解の連続性・不連続性」を表す何らかの指標であると考えるべきでしょう。

　TVD法では一般的に\(r\)は隣接セルの勾配比で定義されます。例えば式\((30),(31)\)中の\({}^L\! r_{i+\frac{1}{2}},{}^R\! r_{i-\frac{1}{2}}\)は次のように与えられます。

　\({}^L\! r_{i+\frac{1}{2}}\)と\({}^R\! r_{i+\frac{1}{2}}\)は分母は一緒ですが、分子は計算される勾配の位置が違います。イメージが付きやすいよう、具体例で可視化してみましょう。

　今、\(\bar{\cal{q}}=(2,1,4,5,7,3)\)と適当におくと、\({}^L\! r_{i+\frac{1}{2}}\)と\({}^R\! r_{i+\frac{1}{2}}\)は以下の図のようなプロファイルとなります。

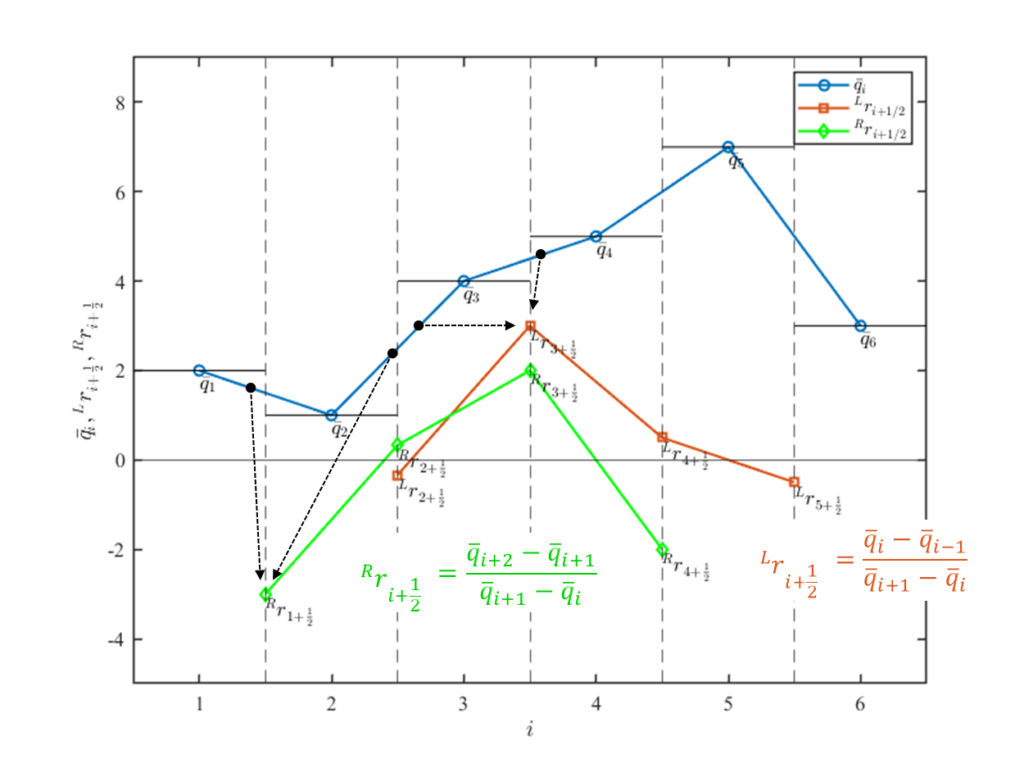
　\({}^L\! r_{i+\frac{1}{2}}\)は注目するセル界面\(i+\frac{1}{2}\)を横切る勾配（\(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}\)）に対し、その左側の勾配（\(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\)）を比にとっています。\({}^R\! r_{i+\frac{1}{2}}\)の場合は右側の勾配（\(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1}\)）を比にとります。

　セル勾配比\(r\)が１に近いとき、隣接セル間で傾きが大きく変わらないので、\(\bar{\cal{q}}\)は滑らかなプロファイルということが出来ます。逆に1から離れていくにしたがって、隣接セル間で傾きが大きく変わるので\(\bar{\cal{q}}\)は不連続なプロファイルに近づいていきます。特にセル勾配比が負になる場合、隣接セル間で逆の傾きを有しているため、\(\bar{\cal{q}}\)は振動的なプロファイルと考えてよいでしょう。

　また、式\((32),(33)\)よりセル勾配比は次のような性質を持ちます。

　TVD法では、以上のようなセル勾配比\(r\)を変数とした勾配リミタ関数を定義することで、\(\bar{\cal{q}}\)のプロファイル形状に応じて空間精度を切り替えます。

勾配リミタ関数の対称性

　次に勾配リミタ関数\(\mathit{\Phi}(r)\)の性質について考えます。式\((33),(34)\)より、式\((28)\)は次のように変形できます。

　ここで\(\delta {}^R\! q_{i-\frac{1}{2}}^{\mathit{\Phi}}\)はリミタ関数を考慮した高次補正量を表し、次式で定義しました。

　同様に式\((29)\)は次のように変形できます。

　ここでセル内での流束の保存性を保つため、次の制約を課すこととします。

　上式は同一セルにおいて、リミタ関数による補正量は左右界面で大きさが等しいことを示しています。このような制約を課すことで、セル界面における流れの流入・流出のバランスが取れ、安定な計算結果を得ることが出来るとされています。要はリミタ関数による補正を好き勝手行ってしまうと「左の界面からはたくさん流れが流入するけど、右の界面からは全然流出しない。」といった物理的におかしい状況が生じうるので、そのような状況を防いでるものと考えられます。

　 上式がいずれのスキーム（\(\kappa\)）に対しても成り立つと仮定すると、式\((36),(38)\)の\((1+\kappa),(1-\kappa)\)の係数が等しいとして、次式が成り立ちます。

　また、式\((34)\)を用いると、上式は次のように書くこともできます。

　式\((40),(41)\)は勾配リミタ関数の対称性と呼ばれ、安定な勾配リミタ関数を設計する上で重要な関係式です。式\((40)\)を式\((35)\)に代入すると界面物理量\({}^R\! q_{i-\frac{1}{2}}\)は次のように計算できます。

　ここで\(i \rightarrow i+1\)と置くと、\({}^R\! q_{i+\frac{1}{2}}\)は次式にて与えられます。

　同様に式\((40)\)を式\((37)\)に代入すると、\({}^L\! q_{i+\frac{1}{2}}\)は次のように表されます。

　上式らはLax-Wendroff法の高次補正項にリミタを掛けた形に一致しています。　Lax-Wendroff法はもともと\(\delta {}^R\! q_{i-\frac{1}{2}}=\delta {}^L\! q_{i+\frac{1}{2}}\)という性質をもつため、対称性の導入により形が一致します。比較用に各種スキームの高次補正項を記載しておきます。(過去記事参照)

　上表と式\((43),(44)\)を比較すると、各種線形解法は勾配リミタ関数\(\mathit{\Phi}\left(r\right)\)を次表のように与えた場合の特殊なケースとして考えられること分かります。

勾配比\(r\)と補正される勾配の対応関係

　さて、ここで一度話を整理します。勾配リミタ関数による補正を受けた界面物理量\({}^R\! q_{i-\frac{1}{2}},{}^L\! q_{i+\frac{1}{2}}\)は\((42),(44)\)より次のように与えられました。

　この時、式\((45)\)において、勾配\(\frac{\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}}{\Delta x}\)は勾配リミタ関数\(\mathit{\Phi}\left({}^R\! r_{i-\frac{1}{2}}\right)\)による制限を受けています。また、式\((46)\)において、勾配\(\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}{\Delta x}\)は勾配リミタ関数\(\mathit{\Phi}\left({}^L\! r_{i+\frac{1}{2}}\right)\)による制限を受けています。

　これらの添え字の関係性は一見分かりずらいので可視化して確認してみましょう。式\((45)\)を模式化すると次のように書けます。

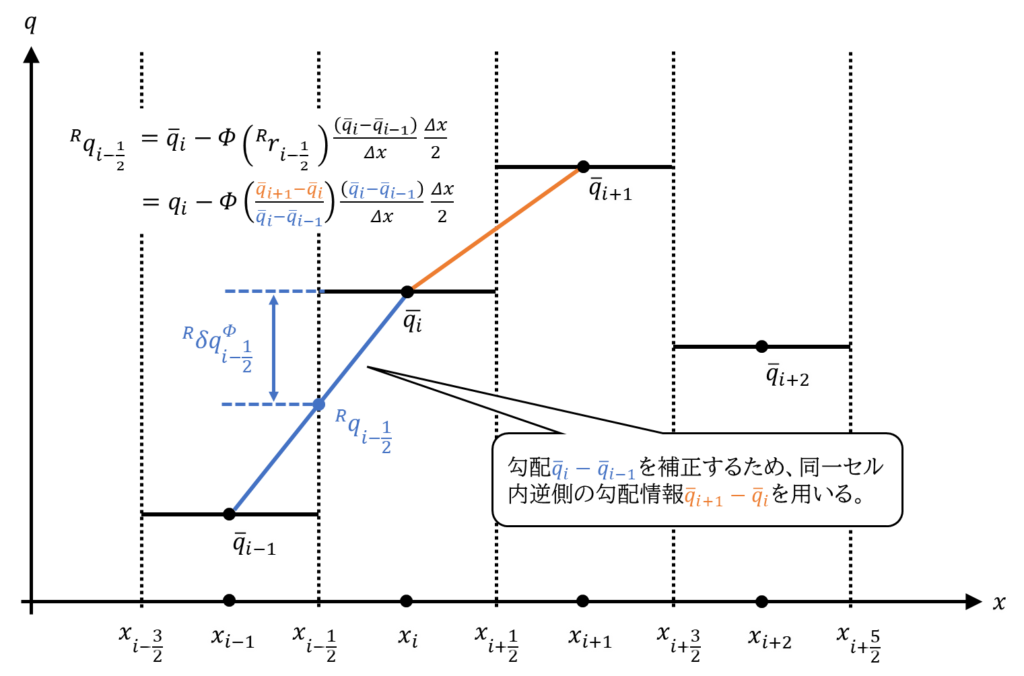
　\(i\)番目のセルの左側界面の値\({}^R\! q_{i-\frac{1}{2}}\)は同界面を横切る直線の勾配\(\frac{\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}}{\Delta x}\)に基づく2次補正量により高精度化されています。さらに、この勾配と右側界面を横切る直線の勾配\(\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}{\Delta x}\)の比\(\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}{\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}}\)に基づき、リミタ関数\(\mathit{\Phi}\left(\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}{\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}}\right)\)による補正を受けています。

　同様に式\((46)\)は次のように書けます。

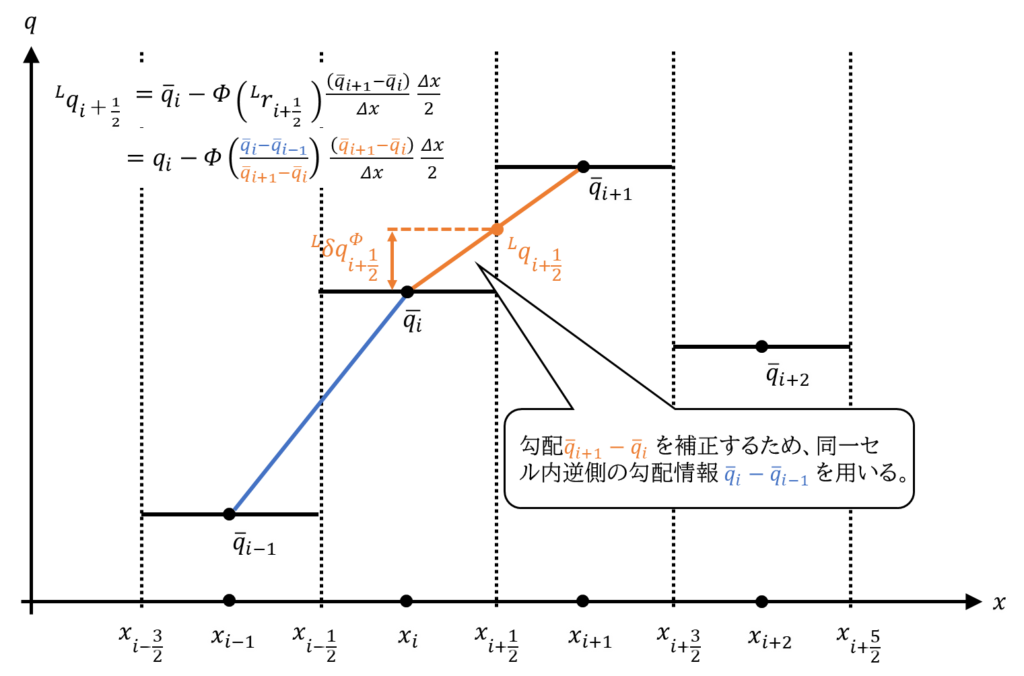
　\(i\)番目のセルの右側界面の値\({}^L\! q_{i+\frac{1}{2}}\)は同界面を横切る直線の勾配\(\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}{\Delta x}\)に基づく2次補正量により高精度化されています。さらに、この勾配と左側界面を横切る直線の勾配\(\frac{\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}}{\Delta x}\)の比\(\frac{\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}}{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}\)に基づき、リミタ関数\(\mathit{\Phi}\left(\frac{\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}}{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}\right)\)による補正を受けています。

　以上より、リミタ関数による補正量は、補正対象となる勾配に対して同一セルの逆側界面における勾配との比から決定されることが分かります。あるセル界面の物理量の補正量を決めるのに、わざわざ異なる隣接セルの勾配情報を用いるのもおかしい気もするので、同一セルの逆側界面の勾配情報を用いるのはある意味自然な流れといってよいでしょう。

勾配リミタ関数のTVD条件

　次にHartenの定理に基づき、数値解がTVDの性質を持つようなリミタ関数\(\mathit{\Phi}(r)\)を考えます。以下の式\((10)\)（再掲）に式\((42)\sim(44)\)を代入します。少々長い式となりますので、右辺の第一項と第二項を分けて考えます。

　まず右辺第一項は式\((44)\)を用いて次のように計算できます。

　同様に右辺第二項は式\((42),(43)\)を用いて次のように計算できます。

　式\((47),(48)\)を式\((10)\)に代入すると、勾配リミタ関数を用いた移流方程式の半離散化式は次のように書くことが出来ます。

　上式がTVD条件を満たしていると仮定した場合、Hartenの定理\((a1)\sim(a3)\)より次式が成り立ちます。

　ここで\(a^{+}>0,a^{-}<0\)の関係を用いていることに注意しましょう。

　式\((50),(51)\)は同等の形をしており、任意の\(r_{1},r_{2}\)を用いると以下のようにまとめられます。

　上式を満たすような勾配リミタ関数\(\mathit{\Phi}\left(r\right)\)を用いることで、TVD条件を満たす安定なスキームを構築できます。これを満たす\(\mathit{\Phi}\left(r\right)\)は無数に存在しますが、実際には次の十分条件が用いられます。

　\(r \leq 0\)の時、\(\bar{\cal{q}}\)のプロファイルは極値を持つ（＝振動的なプロファイル）ので、補間関数を0次に落とし（＝補正なし）、１次精度風上差分を適用することを示しています（表２参照）。また、\(r > 0\)の時、リミタ関数により補正量を空間高次精度項の最大2倍まで引き上げることを示しています。

　これらをグラフ化すると次の通り書けます。青い領域がTVD条件を満たす領域（TVD領域）です。

　さらに表２で示した、Beam-Warming法、Fromm法、Lax-Wendoroff法も付け加えると次のように書けます。

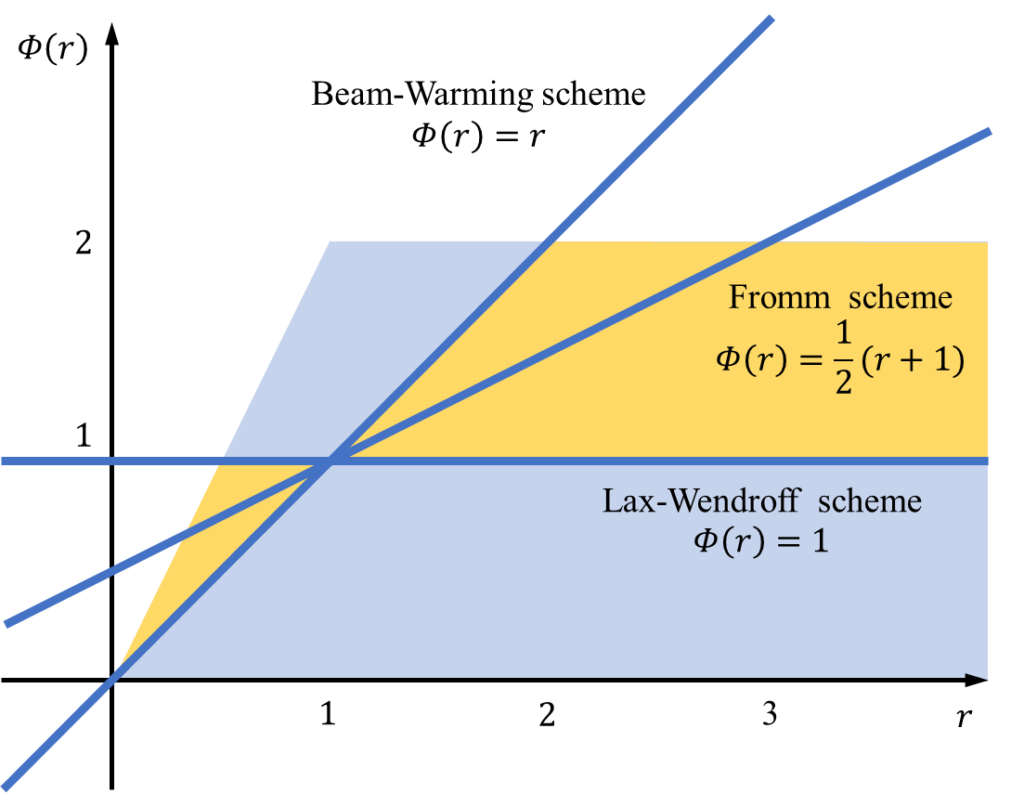
　Beam-Warming法は勾配計算に風上差分、Lax-Wendoroff法の風下勾配を用いる手法であり、Fromm法はこれらの平均として表されました。（過去記事参照）このことは任意の二次精度解法は、Beam-Warming法とLax-Wendoroff法を組み合わせで表すことが出来ることを示しています。したがって、両者が挟む領域内（オレンジの領域）であれば2次精度を有することが出来ます。この領域は2次精度TVD領域と呼ばれ、多くの勾配リミタ関数はこの領域に含まれるように設計されています。

勾配リミタ関数の種類

　一般的によく利用される勾配リミタ関数（4種）について、まとめておきます。いずれのリミタ関数についても、対称性（式\((40),(41)\)）を満たしていることに注意しましょう。（興味があれば計算してみて下さい。）

　minmodリミタ―は2次精度領域の下限を通っています。\(\mathit{\Phi}\left(r\right)\leq1\)なので、リミタ関数による補正は高次精度項を抑制する効果はあっても、増幅させる効果は有していないことが分かります。これは、数値粘性を大きくとり、出来るだけ解を安定側に補正していることを意味しています。

　一方で、Superbeeリミタ―は2次精度領域の上限を通っています。\(r\geq1\)で\(\mathit{\Phi}\left(r\right)\geq1\)なので、リミタ関数による補正は高次精度項を増幅させる効果も有しています。これは、数値粘性を抑えて出来るだけ解をシャープに維持しようとしていることを意味しています。逆に言えば、その分、安定性に問題が生じやすいとも言えます。

　以上2種以外のリミタ―（van Leerリミタ―、van Albadaリミタ―）はこれらの合いの子を取るようなTVD領域を通過しており、２つのリミタ―の中間の性質を持っていると考えてよいでしょう。

　以上でリミタ関数の具体的な形を決めることが出来ました。実際の計算では、式\((28),(29)\)において上記のリミタ関数を適用し、数値流束を計算することで、離散化された移流方程式\((6)\)を解くこととなります。

時間２次精度への適用

　ここまでは、空間２次精度の界面物理量界面物理量\({}^R\! q_{i-\frac{1}{2}},{}^L\! q_{i+\frac{1}{2}}\)（式\((28),(29)\)）に対し、リミタ関数による制限を加える内容でしたが、空間2次精度＋時間２次精度の場合も同様に考えることが出来ます。空間2次精度＋時間２次精度の界面物理量\({}^L\! q_{i+\frac{1}{2}}^{*},{}^R\! q_{i+\frac{1}{2}}^{*}\)は次のように与えられました。（過去記事参照）

　式\((45),(46)\)を例に上式の高次項にリミタ関数を掛けることで、TVD法を構築します。

　あとはこれまでと同様に上式を用いてリーマンソルバにより数値流束を求め、移流方程式\((6)\)を計算すればよいでしょう。

計算結果

　一通り理屈はさらったので、次は実際に線形移流方程式について、1次精度風上差分法、minmodリミタ、superbeeリミタを用いて計算した結果を確認してみましょう。

　初期プロファイルが矩形波である場合、以下のような解が得られます。

　風上差分法（一番左）に比較して、TVD法（右二つ）は抜群に波形を維持できていることが分かります。特に一番右のsuperbeeリミタはほぼ完ぺきに厳密解を再現できているといってよいでしょう。これはsuperbeeリミタがプロファイルの傾きの変化が大きい領域で、大きく補正を掛けるためと考えられます。

　次に初期プロファイルがサイン波である場合、以下のような解が得られます。

　サイン波の場合も矩形波の場合と同様に、風上差分法（一番左）に比較して、TVD法（右二つ）はより厳密解に近い結果を示しています。しかしながら、矩形波の場合はほぼ完ぺきな再現性を見せたsuperbeeリミタは山の頂上がつぶれて、少しおかしなプロファイルとなってしまっています。この感じだと多少は数値粘性があるものの真ん中のminmodリミタのほうが、物理的に自然なプロファイルといってよいかもしれません。superbeeリミタの場合、勾配比に対して補正が強くかかるため、早い段階で勾配が修正され、急激に反対方向に補正された結果、このようなプロファイルになったものと考えられます。

　以上より矩形波のような急峻なプロファイルの場合はsuperbeeリミタが、比較的滑らかなプロファイルの場合は、minmodリミタが優れていると言えそうです。結局、どのようなリミタ関数が適切かは系によってまちまちで、万能なものはないといってよいのでしょう。

MATLABコード

　今回用いたコードは以下の通りです。

% 初期化
clearvars;

% パラメーター
i_max = 100;    % 格子セル数
XL = -1.0;      % 計算領域左端の座標
XR = 1.0;       % 計算領域右端の座標
a = 1.0;        % 線形移流方程式の移流速度
tstop = 2.0;    % 計算停止時刻

% 配列定義
i = 0;                      % セル番号； (i番目セルの左境界の番号はi、右辺境界の番号はi+1とする)
x = zeros(i_max + 1, 1);    % セル境界の座標
u = zeros(i_max, 1);        % セル平均値 （数値解）
ue = zeros(i_max, 1);       % セル平均値 （厳密解）
ul = zeros(i_max + 1, 1);   % セル境界左側の変数値
ur = zeros(i_max + 1, 1);   % セル境界右側の変数値
f = zeros(i_max + 1, 1);    % セル境界の流束
dx = 0;                     % 格子間隔（等間隔とする）
dt = 0;                     % 時間刻み
n = 0;                      % 時間ステップ
t = 0;                      % 計算時間

% 線形移流方程式の初期値を選ぶ
sw1 = 2; %"滑らかな分布（正弦波）：１、"不連続な分布（矩形波）：２

% 流束制限関数を選択する。
method = '1st order UDS';
% method = 'Lax-Wendroff';
% method = 'minmod-limiter';
% method = 'vanLeer-limiter';
% method = 'vanAlbada-limiter';
%method = 'superbee-limiter';

% 格子間隔 計算領域外に二つずつ余分なセルを準備。周期的境界条件向けの設定
dx = (XR - XL) / (i_max - 4.0);

% 時間刻み
dt = 0.2 * dx;

% 計算領域外の２セルも考慮した座標を振る。
x(1) = XL - 2.0 * dx;

% 計算格子，時間刻み，初期条件を設定する
[x, u] = initc(i_max, x, dx, sw1, u);
ue = exact(sw1, i_max, ue, x, a, t, dx);

% メインループ
while t <= tstop

    % 時間発展
    n = n + 1;
    t = t + dt;

    % 空間再構築
    switch method
        case '1st order UDS'
            [ul, ur] = reconstruction_pc(i_max, u, ul, ur);
        case 'Lax-Wendroff'
            [ul, ur] = reconstruction_lw(i_max, u, ul, ur, a, dt, dx);
        case 'minmod-limiter'
            [ul, ur] = reconstruction_minmod(i_max, u, ul, ur, a, dt, dx);
        case 'vanLeer-limiter'
            [ul, ur] = reconstruction_vanLeer(i_max, u, ul, ur, a, dt, dx);
        case 'vanAlbada-limiter'
            [ul, ur] = reconstruction_vanAlbada(i_max, u, ul, ur, a, dt, dx);
        case 'superbee-limiter'
            [ul, ur] = reconstruction_superbee(i_max, u, ul, ur, a, dt, dx);
    end

    % リーマンソルバー
    f = riemann_roe(i_max, a, ul, ur);

    % 時間積分
    [u] = update(i_max, u, dt, dx, f);

    % 境界条件
    [u] = bc(i_max, u);

    % 厳密解
    ue = exact(sw1, i_max, ue, x, a, t, dx);

    % 出力
    fprintf("n=%d, t=%f \n", n, t);

    % 動画保存
    if n == 1
        plotconfig(x(1 : end - 1), ue, u, t, method)
        filename = [method, ', sw = ', num2str(sw1), '.mp4'];
        v = VideoWriter(filename, 'MPEG-4');
        v.FrameRate = 40;
        open(v);
    else
        plotconfig(x(1 : end - 1), ue, u, t, method)
        frame = getframe(gcf);
        writeVideo(v,frame);
    end

end

% 動画ファイルを閉じる
close(v);

%% 以下関数

function [x, u] = initc(i_max, x, dx, sw1, u)

for  i = 2 : i_max + 1
    x(i) = x(i - 1) + dx;% 格子点の座標
end

switch  sw1

    case 1  % 初期の変数値（滑らかな分布）

        for  i = 1 : i_max
            u(i) = 0.5*(1.1 + sin(2.* pi *(x(i)-x(3))));% 三番目の要素（XL、XRの座標値）を基準に考える。
        end

    case 2 % 初期の変数値（不連続な分布）

        for  i = 1 : i_max
            u(i) = 0.1;
        end
        for i = i_max / 2 - 10 : i_max / 2 + 10
            u(i) = 1.0;
        end

    otherwise

        disp("初期値を正しく選択されていません。");

end

end

function [ue] = exact(sw1, i_max, ue, x, a, t, dx)

switch sw1

    case 1 % 初期の変数値（滑らかな分布）
        for i = 1 : i_max
            ue(i) = 0.5 * (1.1 + sin(2. * pi * ((x(i) - x(3)) - a * t)));
        end

    case 2 % 初期の変数値（不連続な分布）
        xc = a * t;
        xl = xc - dx * 10;% 中央に対して10要素だけマイナスに移動した位置

        % 周期境界条件　
        if  xl > 1.0
            xl = -2.0 + xl;
        end

        xr = xc + dx * 10.;

        % 周期境界条件　
        if xr > 1.0
            xr = -2.0 + xr;
        end


        if  xl <= xr
            for  i = 1 : i_max
                ue(i) = 0.1;
                if dx * (i - i_max / 2) >= xl && dx * (i - i_max / 2) <= xr
                    ue(i) = 1.0;
                end
            end
        end

        if xl >= xr
            for i = 1 : i_max
                ue(i) = 1.0;
                if dx * (i - i_max / 2) >= xr && dx * (i - i_max / 2) <= xl
                    ue(i) = 0.1;
                end
            end
        end

end
end

function [ul, ur] = reconstruction_pc(i_max, u, ul, ur)

for i = 2 : i_max - 2
    ul(i + 1) = u(i); % セル境界(i+1/2)左側の値
    ur(i + 1) = u(i + 1); % セル境界(i+1/2)右側の値
end

end

function [ul, ur] = reconstruction_lw(i_max, u, ul, ur, a, dt, dx)

for i = 2 : i_max - 2
    alpha_12 = a;
    deltaL = 0.5 * (u(i + 1) - u(i));
    deltaR = 0.5 * (u(i + 1) - u(i));
    ul(i + 1) = u(i) + (1.0 - alpha_12 * dt / dx) * deltaL; % セル境界(i+1/2)左側の値
    ur(i + 1) = u(i + 1) - (1.0 + alpha_12*dt / dx) * deltaR; % セル境界(i+1/2)右側の値
end

end

function [f] = riemann_roe(i_max, a, ul, ur) % 流束を計算する

for  i = 3 : i_max - 1
    f(i) = 1.0 / 2.0 * (a * ul(i) + a * ur(i)) - 1.0 / 2.0 * abs(a) * (ur(i) - ul(i));
end

end

function [u] = update(i_max, u, dt, dx, f)

for  i = 3 : i_max - 2
    u(i) = u(i) - dt / dx * (f(i + 1) - f(i));% 更新する
end

end

function [u] = bc(i_max, u) % 周期境界条件

u(1) = u(i_max - 3); % 計算領域左端の境界条件
u(2) = u(i_max - 2); % 計算領域左端の境界条件
u(i_max - 1) = u(3); % 計算領域右端の境界条件
u(i_max) = u(4); % 計算領域右端の境界条件

end

function [] = plotconfig(x, ue, u, t, method)

plot(x, ue, x, u)
%plot(x, u)

title(['time = ', num2str(t, '%.3f')]);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 12);
axis equal;
axis tight;
axis on;
fig=gcf;
fig.Color='white';
ylim([-0.2 1.4]);
xlabel('x')
ylabel('u')

% 凡例
legend({'exact', method},'Location','southwest','FontSize', 10)
%legend({'exact'},'Location','southwest','FontSize', 10)

% 動画作成のおまじない
set(gca,'nextplot','replacechildren');

end

function [ul, ur] = reconstruction_minmod(i_max, u, ul, ur, a, dt, dx)

for i = 2 : i_max - 2
    % セル境界(i+1/2)の左側の勾配比
    rL = (u(i) - u(i - 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);% ゼロ割が発生しないように微小量を足す。
    % セル境界(i+1/2)の右側の勾配比
    rR = (u(i + 2) - u(i + 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);
    phiL = minmod(rL);
    phiR = minmod(rR);
    deltaL = 0.5 * (u(i + 1) - u(i));
    deltaR = 0.5 * (u(i + 1) - u(i));
    alpha_12 = a;
    ul(i + 1) = u(i) + (1.0 - alpha_12 * dt / dx) * phiL * deltaL;% セル境界(i+1/2)左側の値
    ur(i + 1) = u(i + 1) - (1.0 + alpha_12 * dt / dx) * phiR * deltaR;% セル境界(i+1/2)右側の値
end

end

function [a] = minmod(x)

a = max(0.0, min(1.0, x));

end

function [a] = signfunc(x)

if x >= 0
    a = 1;
else
    a = -1;
end

end

function [ul, ur] = reconstruction_vanLeer(i_max, u, ul, ur, a, dt, dx)

for  i = 2 : i_max - 2
    % セル境界(i+1/2)の左側の勾配比
    rL = (u(i) - u(i - 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);
    % セル境界(i+1/2)の右側の勾配比
    rR = (u(i + 2) - u(i + 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);
    phiL = vanLeer(rL);
    phiR = vanLeer(rR);
    deltaL = 0.5 * (u(i + 1) - u(i));
    deltaR = 0.5 * (u(i + 1) - u(i));
    alpha_12 = a;
    ul(i + 1) = u(i) + (1.0 - alpha_12 * dt / dx) * phiL * deltaL;% セル境界(i+1/2)左側の値
    ur(i + 1) = u(i + 1) - (1.0 + alpha_12 * dt / dx) * phiR * deltaR;% セル境界(i+1/2)右側の値
end

end

function [a] = vanLeer(x) % van Leer limiter
a = (x + abs(x)) / (1 + abs(x));
end

function [ul, ur] = reconstruction_vanAlbada(i_max, u, ul, ur, a, dt, dx)

for  i = 2 : i_max - 2
    % セル境界(i+1/2)の左側の勾配比
    rL = (u(i) - u(i - 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);
    % セル境界(i+1/2)の右側の勾配比
    rR = (u(i + 2) - u(i + 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);
    phiL = vanAlbada(rL);
    phiR = vanAlbada(rR);
    deltaL = 0.5 * (u(i + 1) - u(i));
    deltaR = 0.5 * (u(i + 1) - u(i));
    alpha_12 = a;
    ul(i + 1) = u(i) + (1.0 - alpha_12 * dt / dx) * phiL * deltaL; % セル境界(i+1/2)左側の値
    ur(i + 1) = u(i + 1) - (1.0 + alpha_12 * dt / dx) * phiR * deltaR; % セル境界(i+1/2)右側の値
end

end

function[a] = vanAlbada(x) % van Albada limiter
a = (x + x * x) / (1 + x * x);
end


function [ul, ur] = reconstruction_superbee(i_max, u, ul, ur, a, dt, dx)

for  i = 2 : i_max - 2
    % セル境界(i+1/2)の左側の勾配比
    rL = (u(i) - u(i - 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);
    % セル境界(i+1/2)の右側の勾配比
    rR = (u(i + 2) - u(i + 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);
    phiL = superbee(rL);
    phiR = superbee(rR);
    deltaL = 0.5 * (u(i + 1) - u(i));
    deltaR = 0.5 * (u(i + 1) - u(i));
    alpha_12 = a;
    ul(i + 1) = u(i) + (1.0 - alpha_12 * dt / dx) * phiL * deltaL; % セル境界(i+1/2)左側の値
    ur(i + 1) = u(i + 1) - (1.0 + alpha_12 * dt / dx) * phiR * deltaR; % セル境界(i+1/2)右側の値
end

end

function[a] = superbee(x)% Superbee limiter

a = max(max(0.0, min(1.0, 2.0 * x)), min(2.0, x));

end

おわりに

　今回は非線形解法の一種であるTVD法についてまとめました。一般的な教科書だと、TVD法は略式で導出されることが多く、どこか唐突だったり、腑に落ちない箇所がある場合が多い気がします。今回はできるだけ式変形や証明を省略せず、自分なりに納得が得られる内容になるよう意識しました。その分大分長くなってしまいましたが…。

　今回の記事で一通りの内容を終えたので、「有限体積法の基礎」のシリーズは一旦終了としたいと思います。今後は別記事の中で、これらの内容を活用・発展させていく予定です。

参考文献

[1] 肖 鋒, “数値流体解析の基礎- Visual C++とgnuplotによる圧縮性・非圧縮性流体解析 -“, コロナ社, 2020
[2] C. Hirsch, “Numerical Computation of Internal and External Flows Volume 2: Computational Methods for Inviscid and Viscous Flows“ , John Wiley & Son Ltd , 1990/05