はじめに
過去の記事では1次元線形移流方程式をTVD法で計算しました。今回は2次元線形移流方程式について、TVD法をはじめとした様々な移流スキームで解き、その性質について比較・考察したいと思います。
有限体積法による2次元線形移流方程式の離散化
2次元移流方程式は次式にて与えられます。
\frac{\partial q}{\partial t}+a_{x}\frac{\partial q}{\partial x}+a_{y}\frac{\partial q}{\partial y}= 0\tag{1}
\end{align}
2次元の微分演算子を用いると以下のような保存則の形式として書くこともできます。
\frac{\partial q}{\partial t}+ \mathrm{div} \left(\boldsymbol{a}q\right)=0\tag{2}
\end{align}
上式について、1次元の時と同様に有限体積法で離散化します。2次元の有限体積法では、離散変数がセル\(CV\)内での空間平均値として次のように与えられることに注意しましょう。
\bar{q}_{i,j}(t)=\frac{1}{\Delta V}\left(\int_{CV_{i,j}}q\left(x,y,t\right)dV\right)
\tag{3}
\end{align}
ここで、今回は2次元を考えているので、\(z\)方向は有限の厚み\(\delta\)とし、\(dV=\delta dxdy\)と置くこととします。
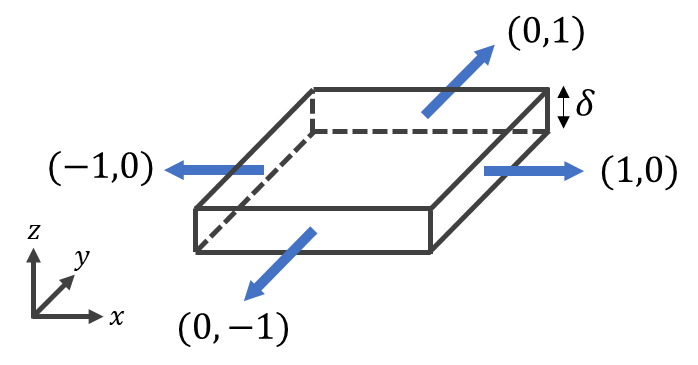
まず初めに式\((2)\)を積分し、単一セル空間・微小時間に関して平均化します。
\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}&\int_{CV_{i,j}}\left\{\frac{\partial q}{\partial t}+ \mathrm{div} \left(\boldsymbol{a}q\right)\right\}dVdt=0\tag{4}
\end{align}
上式について積分を実行します。まず左辺第一項から計算します。
(式(4)左辺第一項)&=\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int_{CV_{i,j}}\left(\frac{\partial q}{\partial t}\right)dVdt\\
&= \frac{1}{\Delta t}\frac{\partial }{\partial t}\int_{t}^{t+\Delta t} \frac{1}{\Delta V}\left(\int_{CV_{i,j}}qdV\right)dt
\\
&= \frac{1}{\Delta t}\frac{\partial }{\partial t}\int_{t}^{t+\Delta t}\bar{q}_{i,j}dt\\
&= \frac{1}{\Delta t}\left[\bar{q}_{i,j}(t)\right]_{t}^{t+\Delta t}\\
&= \frac{\bar{q}_{i,j}(t+\Delta t)-\bar{q}_{i,j}(t)}{\Delta t}\\
&= \frac{\bar{q}_{i,j}^{n+1}-\bar{q}_{i,j}^{n}}{\Delta t}
\tag{5}
\end{align}
2行目から3行目の変形には式\((3)\)を用いました。
次に式\((4)\)の左辺第二項について考えます。ガウスの発散定理を用いて、発散の体積分を面積分へと変換します。
(式(4)左辺第二項)&=\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int_{CV_{i,j}} \mathrm{div} \left(\boldsymbol{a}q\right)dVdt\\
&=\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int q\boldsymbol{a}\cdot \boldsymbol{n}dSdt\\
&=\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\left\{\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
q\left(x_{i+\frac{1}{2}},y\right)
\left(
\begin{array}{c}
a_{x} \\
a_{y}
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
1 \\
0
\end{array}
\right)
\delta dy
+
\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
q\left(x_{i-\frac{1}{2}},y\right)
\left(
\begin{array}{c}
a_{x} \\
a_{y}
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
-1 \\
0
\end{array}
\right)
\delta dy
\right.\\
&\quad\quad\quad\quad\quad\quad\quad\quad\quad
+
\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}
\left.
q\left(x,y_{j+\frac{1}{2}}\right)
\left(
\begin{array}{c}
a_{x} \\
a_{y}
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
0 \\
1
\end{array}
\right)
\delta dx
+
\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}
q\left(x,y_{j-\frac{1}{2}}\right)
\left(
\begin{array}{c}
a_{x} \\
a_{y}
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
0 \\
-1
\end{array}
\right)
\delta dx
\right\}dt\\
&=\frac{1}{\Delta x \Delta y \Delta t}\int_{t}^{t+\Delta t}\left\{\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
a_{x} q\left(x_{i+\frac{1}{2}},y\right)
dy
–
\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
a_{x} q\left(x_{i-\frac{1}{2}},y\right)
dy
\right.\\
&\quad\quad\quad\quad\quad\quad\quad\quad\quad
+
\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}
\left.
a_{y} q\left(x,y_{j+\frac{1}{2}}\right)
dx
–
\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}
a_{y} q\left(x,y_{j-\frac{1}{2}}\right)
dx
\right\}dt
\tag{6}
\end{align}
最後の行では、\(\Delta V =\delta\Delta x \Delta y \)の関係式を用いました。
例えば、右辺中括弧内1項目の\(\frac{1}{\Delta y}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
a_{x} q\left(x_{i+\frac{1}{2}},y\right)
dy\)は\(x_{i+\frac{1}{2}}\)セル界面における\(a_{x} q\left(x_{i+\frac{1}{2}},y\right)\)の\(y\)に関する平均値を示しています。これはセル界面を単位時間に通過する物理量の総和であり、数値流束\(f_{i+\frac{1}{2},j}\)に他なりません。2~3項目も同様の記号で表すと式\((6)\)は次のように書けます。
&=\frac{1}{\Delta t}\int_{t}^{t+\Delta t}\left(\frac{f_{i+\frac{1}{2},j}
–
f_{i-\frac{1}{2},j}}{\Delta x}
+
\frac{
f_{i,j+\frac{1}{2}}
–
f_{i,j-\frac{1}{2}}}{\Delta y}
\right)dt
\tag{7}
\end{align}
ここで、\(f_{i+\frac{1}{2},j},f_{i-\frac{1}{2},j},f_{i,j+\frac{1}{2}},f_{i,j-\frac{1}{2}}\)はそれぞれ次の通りです。
f_{i+\frac{1}{2},j}=\frac{1}{\Delta y}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
a_{x} q\left(x_{i+\frac{1}{2}},y\right)
dy\tag{8}\\
f_{i-\frac{1}{2},j}=\frac{1}{\Delta y}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
a_{x} q\left(x_{i-\frac{1}{2}},y\right)
dy\tag{9}\\
f_{i,j+\frac{1}{2}}=\frac{1}{\Delta x}\int_{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}
a_{y} q\left(x,y_{j+\frac{1}{2}}\right)
dx\tag{10}\\
f_{i,j-\frac{1}{2}}=\frac{1}{\Delta x}\int_{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}
a_{y} q\left(x,y_{j-\frac{1}{2}}\right)
dx\tag{11}\\
\end{align}
次に式\((7)\)の時間積分について考えます。本来、数値流束\(f_{i+\frac{1}{2},j}\)は時間に依存するため、時間の関数として表現したうえで積分を実行すべきです。ただし、数値流束は時間方向にも離散化されているため、離散化された数値流束\(f_{i+\frac{1}{2},j}^{n}\)や\(f_{i+\frac{1}{2},j}^{n+1}\)などを用いて数値流束\(f_{i+\frac{1}{2},j}\)の時間依存性を表現する必要があります。
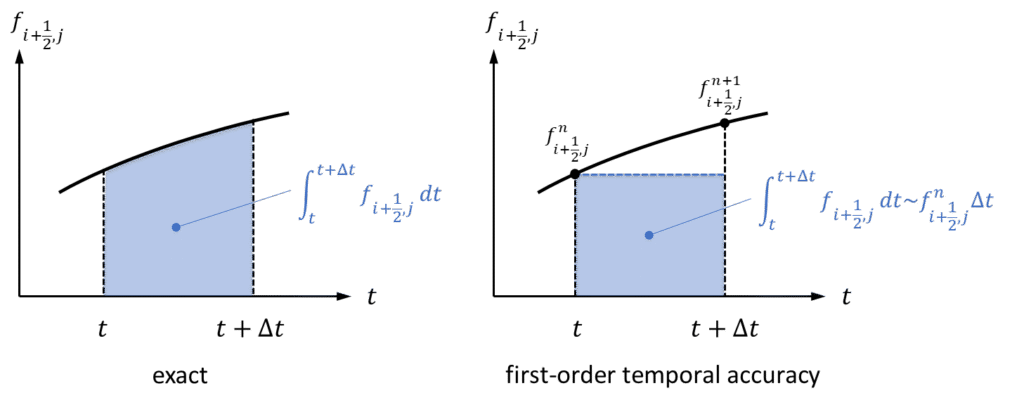
今回は時間一次精度とし、\(t \sim t + \Delta t\)の間の時間変動は考慮しない(\(f_{i+\frac{1}{2},j}=f_{i+\frac{1}{2},j}^{n}\))ものとして、計算することとします。このとき、数値流束は定数として積分の外に出すことが出来ます。
&=\frac{1}{\Delta t}\left(\frac{f_{i+\frac{1}{2},j}^{n}
–
f_{i-\frac{1}{2},j}^{n}}{\Delta x}
+
\frac{
f_{i,j+\frac{1}{2}}^{n}
–
f_{i,j-\frac{1}{2}}^{n}}{\Delta y}
\right)\int_{t}^{t+\Delta t}dt\\
&=\frac{f_{i+\frac{1}{2},j}^{n}
–
f_{i-\frac{1}{2},j}^{n}}{\Delta x}
+
\frac{
f_{i,j+\frac{1}{2}}^{n}
–
f_{i,j-\frac{1}{2}}^{n}}{\Delta y}
\tag{12}
\end{align}
以上、式\((5),(12)\)を式\((4)\)に代入すると、
&\frac{\bar{q}_{i,j}^{n+1}-\bar{q}_{i,j}^{n}}{\Delta t}+\frac{ f_{i+\frac{1}{2},j}-f_{i-\frac{1}{2},j}}{\Delta x}+\frac{ f_{i,j+\frac{1}{2}}-f_{i,j-\frac{1}{2},}}{\Delta y}= 0\\
&\Leftrightarrow\bar{q}_{i,j}^{n+1}=\bar{q}_{i,j}^{n}-\Delta t\left(\frac{ f_{i+\frac{1}{2},j}-f_{i-\frac{1}{2},j}}{\Delta x}+\frac{ f_{i,j+\frac{1}{2}}-f_{i,j-\frac{1}{2},}}{\Delta y}\right)\tag{13}
\end{align}
上式が有限体積法により離散化された2次元移流方程式です。
界面物理量の2次元化
式\((13)\)を解くには数値流束\( f_{i,j+\frac{1}{2}},f_{i,j-\frac{1}{2},}\)を離散変数\(\bar{q}_{i,j}\)で表現しなくてはいけません。この関係式はリーマンソルバで与えられますが、リーマンソルバは界面物理量で表現されるので、まずは界面物理量を2次元化しましょう。
界面物理量の導出は物理量のセル平均値を補間関数で表現する部分から始まります。1次元の場合の補間関数\(Q_i(x)\)は次式で定義されました。(過去記事参照)
\bar{\cal{q}}_{i}=\frac{1}{\Delta x}\int_{i-\frac{1}{2}}^{i+\frac{1}{2}}Q_i(x)dx \tag{14}
\end{align}
これを2次元に拡張する場合、2次元補間関数\(Q_{i,j}(x,y)\)を用いて次のように書くのが自然でしょう。
\bar{\cal{q}}_{i,j}=\frac{1}{\Delta x \Delta y}\int_{x_{i-\frac{1}{2}},j}^{x_{i+\frac{1}{2},j}}\int_{y_{i,j-\frac{1}{2}}}^{y_{i,j+\frac{1}{2}}}Q_{i,j}(x,y)dxdy \tag{15}
\end{align}
上式について1次元の時と同様に、\(x\)方向の左側界面\(x_{i-\frac{1}{2},j}\)における界面物理量\({}^R\! q_{i-\frac{1}{2},j}\)を求めます。
まずは\(Q_{i,j}(x,y)\)を\(x_{i-\frac{1}{2},j}\)においてテイラー展開します。このとき変数\(y\)は未知変数のままとし、展開はしないこととします。
Q_{i,j}(x,y)&=Q_{i,j}\left(x_{i-\frac{1}{2}},y\right)+\frac{\partial Q_{i,j}}{\partial x}\left(x_{i-\frac{1}{2}},y\right) \left(x-x_{i-\frac{1}{2}}\right)\\
&\quad\quad+\frac{1}{2}\frac{\partial^2 Q_{i,j}}{\partial x^2}\left({x_{i-\frac{1}{2}},y}\right)\left(x-x_{i-\frac{1}{2}}\right)^2+O\left(\left(x-x_{i-\frac{1}{2}}\right)^3\right)\tag{16}
\end{align}
両辺をセル\(i\)内で積分し、\(\Delta x_{i,j}\Delta y_{i,j}\)で割ることで左辺をセル平均\(\bar{\cal{q}}_{i,j}\)(式\((15)\))を用いて表現します。
\bar{\cal{q}}_{i,j}&=\frac{1}{\Delta x_{i,j}\Delta y_{i,j}}\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}dx\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}Q_{i,j}\left(x_{i-\frac{1}{2}},y\right)dy\\
& \quad\quad+\frac{1}{\Delta x_{i,j} \Delta y_{i,j}}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\frac{\partial Q_{i,j}}{\partial x}\left(x_{i-\frac{1}{2}},y\right)dy\int_{x_{i-\frac{1}{2},j}}^{x_{i+\frac{1}{2},j}} \left(x-x_{i-\frac{1}{2}}\right)dx\\
&\quad\quad\quad+\frac{1}{2\Delta x_{i,j}\Delta y_{i,j}}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\frac{\partial^2 Q_{i,j}}{\partial x^2}\left({x_{i-\frac{1}{2}},y}\right)dy\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left(x-x_{i-\frac{1}{2}}\right)^2dx\\
&\quad\quad\quad\quad+\frac{1}{\Delta x_{i,j} \Delta y_{i,j}}\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}O\left(\left(x-x_{i-\frac{1}{2}}\right)^3\right)dx\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}dy
\tag{17}
\end{align}
上式右辺では、\(x,y\)の積分はそれぞれ影響のある項のみにかかるように変形しています。このような操作が可能なのは、今回の系が2次元直交格子で離散化されており、セル界面が単一の\(x\)座標または\(y\)座標で表されるためです。非構造格子の場合、セル界面において\(x,y\)座標両方が同時に変化するため、上式のように積分を分離できないことに注意しましょう。
ここで\(x\)方向の補間関数\(Q_{i,j}\left(x\right)\)を次のように定義します。
Q_{i,j}\left(x\right)&=\frac{1}{\Delta y_{i,j}}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}Q_{i,j}\left(x,y\right)dy\tag{18}
\end{align}
\(Q_{i,j}\left(x,y\right)\)の値は、当然\(y\)座標によっても変化するわけですが、上式は\(y\)に関して、単一セル内で積分することで平均化して扱うことを示しています。
また、上式を用いて、左側界面\(x_{i-\frac{1}{2},j}\)における界面物理量\({}^R\! q_{i-\frac{1}{2},j}\)を次のように定義します。
{}^R\! q_{i-\frac{1}{2},j}&=Q_{i,j}\left(x_{i-\frac{1}{2}}\right)=\frac{1}{\Delta y_{i,j}}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}Q_{i,j}\left(x_{i-\frac{1}{2}},y\right)dy
\tag{19}
\end{align}
このように定義することで、1次元の補間関数と同様の扱いをすることができます。これを式\((15)\)に代入します。
\bar{\cal{q}}_{i,j}&=\frac{{}^R\! q_{i-\frac{1}{2},j}}{\Delta x_{i,j}}\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}dx \\
& \quad\quad+\frac{1}{\Delta x_{i,j} }\frac{\partial Q_{i,j}}{\partial x}\left(x_{i-\frac{1}{2}}\right)\int_{x_{i-\frac{1}{2},j}}^{x_{i+\frac{1}{2},j}} \left(x-x_{i-\frac{1}{2}}\right)dx\\
&\quad\quad\quad+\frac{1}{2\Delta x_{i,j}}\frac{\partial^2 Q_{i,j}}{\partial x^2}\left({x_{i-\frac{1}{2}}}\right)\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left(x-x_{i-\frac{1}{2}}\right)^2dx\\
&\quad\quad\quad\quad+\frac{1}{\Delta x_{i,j} \Delta y_{i,j}}\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}O\left(\left(x-x_{i-\frac{1}{2}}\right)^3\right)dx\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}dy
\tag{20}
\end{align}
ここで積分は\(A=x-x_{i-\frac{1}{2},j}\)とおき置換積分で計算します。また、\(\Delta x_{i,j}=x_{i+\frac{1}{2},j}-x_{i-\frac{1}{2},j}\)と置くことにします。
\bar{\cal{q}}_{i,j}&={}^R\! q_{i-\frac{1}{2},j}+\frac{1}{\Delta x_{i,j}}\frac{\partial Q_{i,j}}{\partial x}\left(x_{i-\frac{1}{2}}\right) \int_{0}^{\Delta x_{i,j}}AdA
\\
&\quad\quad\quad\quad\quad\quad+\frac{1}{2\Delta x_{i,j}}\frac{\partial^2 Q_{i,j}}{\partial x^2}\left(x_{i-\frac{1}{2}}\right)\int_{0}^{\Delta x_{i,j}}A^2dA+\frac{1}{\Delta x_{i,j}}\int_{0}^{\Delta x_{i,j}}O\left(A^3\right)dA\\
&={}^R\! q_{i-\frac{1}{2},j}+\frac{1}{\Delta x_{i,j}}\frac{\partial Q_{i,j}}{\partial x}\left(x_{i-\frac{1}{2}}\right)\left[\frac{1}{2}A^2\right]_{0}^{\Delta x_{i,j}}
\\
&\quad\quad\quad\quad\quad\quad+\frac{1}{2\Delta x_{i,j}}\frac{\partial^2 Q_{i,j}}{\partial x^2}\left(x_{i-\frac{1}{2}}\right)\left[\frac{1}{3}A^3\right]_{0}^{\Delta x_{i,j}}+\frac{1}{\Delta x_{i,j}}O\left(\left[\frac{1}{4}A^4\right]_{0}^{\Delta x_{i,j}}\right)\\
&={}^R\! q_{i-\frac{1}{2},j}+\frac{1}{2}\frac{\partial Q_{i,j}}{\partial x}\left(x_{i-\frac{1}{2}}\right)\Delta x_{i,j}+\frac{1}{6}\frac{\partial^2 Q_{i,j}}{\partial x^2}\left(x_{i-\frac{1}{2}}\right)\left(\Delta x_{i,j}\right)^2+O\left(\left(\Delta x_{i,j}\right)^3\right)
\tag{21}
\end{align}
数値流束の計算で必要なのは右辺第一項の界面物理量\({}^R\! q_{i-\frac{1}{2},j}\)なので、これについてまとめます。
{}^R\! q_{i-\frac{1}{2},j}=\bar{\cal{q}}_{i,j}-\frac{1}{2}\frac{\partial Q_{i,j}}{\partial x}\left(x_{i-\frac{1}{2}}\right) \Delta x_{i,j}-\frac{1}{6}\frac{\partial^2 Q_{i,j}}{\partial x^2}\left(x_{i-\frac{1}{2}}\right) \left(\Delta x_{i,j}\right)^2+O\left(\left(\Delta x_{i,j}\right)^3\right)
\tag{22}
\end{align}
上式は\(y\)方向の平均化された補間関数\(Q_{i,j}\left(x_{i-\frac{1}{2}}\right)\)(式\((19)\))を用いるものの、1次元の式と全く同じ形をしています(過去記事参照)。したがって、これ以降は1次元の場合と同等なロジックでTVD法まで定式化することができます。
例えば、1次元の場合、空間・時間高次精度化された界面物理量\({}^L\! q_{i+\frac{1}{2}},{}^R\! q_{i+\frac{1}{2}}\)は次のように書けました。
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}
+\left(1-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right)\left[\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1})+\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i})\right]\tag{21}\\
{}^R\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i+1}
-\left(1+\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right)\left[\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i})+\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1})\right]
\tag{24}
\end{align}
これらを2次元化すると各成分について以下のように書けます。
- \(x\)成分
{}^L\! q_{i+\frac{1}{2},j}&=\bar{\cal{q}}_{i,j}
+\left(1-\frac{\alpha_{i+\frac{1}{2},j}\Delta t}{\Delta x}\right)\left[\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i,j}-\bar{\cal{q}}_{i-1,j})+\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i+1,j}-\bar{\cal{q}}_{i,j})\right]\tag{25}\\
{}^R\! q_{i+\frac{1}{2},j}&=\bar{\cal{q}}_{i+1,j}
-\left(1+\frac{\alpha_{i+\frac{1}{2},j}\Delta t}{\Delta x}\right)\left[\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i+1,j}-\bar{\cal{q}}_{i,j})+\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i+2,j}-\bar{\cal{q}}_{i+1,j})\right]
\tag{26}
\end{align}
- \(y\)成分
{}^L\! q_{i,j+\frac{1}{2}}&=\bar{\cal{q}}_{i,j}
+\left(1-\frac{\alpha_{i,j+\frac{1}{2}}\Delta t}{\Delta x}\right)\left[\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i,j}-\bar{\cal{q}}_{i,j-1})+\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i,j+1}-\bar{\cal{q}}_{i,j})\right]\tag{27}\\
{}^R\! q_{i,j+\frac{1}{2}}&=\bar{\cal{q}}_{i,j+1}
-\left(1+\frac{\alpha_{i,j+\frac{1}{2}}\Delta t}{\Delta x}\right)\left[\frac{1}{4}(1+\kappa)(\bar{\cal{q}}_{i,j+1}-\bar{\cal{q}}_{i,j})+\frac{1}{4}(1-\kappa)(\bar{\cal{q}}_{i,j+2}-\bar{\cal{q}}_{i,j+1})\right]
\tag{28}
\end{align}
今回の場合、\(\alpha_{i+\frac{1}{2},j}=a_{x},\alpha_{i,j+\frac{1}{2}}=a_{y}\)とすればよいでしょう。
同様にTVD法による界面物理量も2次元化できます。1次元TVD法における界面物理量\({}^L\! q_{i+\frac{1}{2}}^{*},{}^R\! q_{i+\frac{1}{2}}^{*}\)は次のように書けました。(過去記事参照)
{}^L\! q_{i+\frac{1}{2}}^{*}&=\bar{\cal{q}}_{i}^{n}+\left(1-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right)\mathit{\Phi}\left({}^L\! r_{i+\frac{1}{2}}\right){}^L\delta q_{i+\frac{1}{2}}^{n}\\
&=\bar{\cal{q}}_{i}^{n}+\left(1-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right)\mathit{\Phi}\left({}^L\! r_{i+\frac{1}{2}}\right)\left(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}\right)\tag{29}\\
{}^R\! q_{i+\frac{1}{2}}^{*}&=\bar{\cal{q}}_{i+1}^{n}-\left(1+\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right)\mathit{\Phi}\left({}^R\! r_{i+\frac{1}{2}}\right){}^R\delta q_{i+\frac{1}{2}}^{n}\\
&=\bar{\cal{q}}_{i+1}^{n}-\left(1+\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right)\mathit{\Phi}\left({}^R\! r_{i+\frac{1}{2}}\right)\left(\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}\right)
\tag{30}\\
{}^L\! r_{i+\frac{1}{2}}&=\frac{\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}}{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}
\tag{31}\\
{}^R\! r_{i+\frac{1}{2}}&=\frac{\bar{\cal{q}}_{i+2}-\bar{\cal{q}}_{i+1}}{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}\quad\quad \left({}^R\! r_{i-\frac{1}{2}}=\frac{\bar{\cal{q}}_{i+1}-\bar{\cal{q}}_{i}}{\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}}\right)\tag{32}\\
\end{align}
したがって、2次元の場合、単純な拡張で次のように書けるでしょう。
- \(x\)成分
{}^L\! q_{i+\frac{1}{2},j}^{*}&=\bar{\cal{q}}_{i,j}^{n}+\left(1-\frac{\alpha_{i+\frac{1}{2},j}\Delta t}{\Delta x}\right)\mathit{\Phi}\left({}^L\! r_{i+\frac{1}{2},j}\right)\left(\bar{\cal{q}}_{i+1,j}-\bar{\cal{q}}_{i,j}\right)\tag{33}\\
{}^R\! q_{i+\frac{1}{2},j}^{*}&=\bar{\cal{q}}_{i+1,j}^{n}-\left(1+\frac{\alpha_{i+\frac{1}{2},j}\Delta t}{\Delta x}\right)\mathit{\Phi}\left({}^R\! r_{i+\frac{1}{2},j}\right)\left(\bar{\cal{q}}_{i+1,j}-\bar{\cal{q}}_{i,j}\right)\tag{34}\\
{}^L\! r_{i+\frac{1}{2},j}&=\frac{\bar{\cal{q}}_{i,j}-\bar{\cal{q}}_{i-1,j}}{\bar{\cal{q}}_{i+1,j}-\bar{\cal{q}}_{i,j}}
\tag{35}\\
{}^R\! r_{i+\frac{1}{2},j}&=\frac{\bar{\cal{q}}_{i+2,j}-\bar{\cal{q}}_{i+1,j}}{\bar{\cal{q}}_{i+1,j}-\bar{\cal{q}}_{i,j}}\quad\quad \left({}^R\! r_{i-\frac{1}{2},j}=\frac{\bar{\cal{q}}_{i+1,j}-\bar{\cal{q}}_{i,j}}{\bar{\cal{q}}_{i,j}-\bar{\cal{q}}_{i-1,j}}\right)\tag{36}
\end{align}
- \(y\)成分
{}^L\! q_{i,j+\frac{1}{2}}^{*}&=\bar{\cal{q}}_{i,j}^{n}+\left(1-\frac{\alpha_{i,j+\frac{1}{2}}\Delta t}{\Delta x}\right)\mathit{\Phi}\left({}^L\! r_{i,j+\frac{1}{2}}\right)\left(\bar{\cal{q}}_{i,j+1}-\bar{\cal{q}}_{i,j}\right)\tag{37}\\
{}^R\! q_{i,j+\frac{1}{2}}^{*}&=\bar{\cal{q}}_{i,j+1}^{n}-\left(1+\frac{\alpha_{i,j+\frac{1}{2}}\Delta t}{\Delta x}\right)\mathit{\Phi}\left({}^R\! r_{i,j+\frac{1}{2}}\right)\left(\bar{\cal{q}}_{i,j+1}-\bar{\cal{q}}_{i,j}\right)\tag{38}\\
{}^L\! r_{i,j+\frac{1}{2}}&=\frac{\bar{\cal{q}}_{i,j}-\bar{\cal{q}}_{i,j-1}}{\bar{\cal{q}}_{i,j+1}-\bar{\cal{q}}_{i,j}}
\tag{39}\\
{}^R\! r_{i,j+\frac{1}{2}}&=\frac{\bar{\cal{q}}_{i,j+2}-\bar{\cal{q}}_{i,j+1}}{\bar{\cal{q}}_{i,j+1}-\bar{\cal{q}}_{i,j}}\quad\quad \left({}^R\! r_{i,j-\frac{1}{2}}=\frac{\bar{\cal{q}}_{i,j+1}-\bar{\cal{q}}_{i,j}}{\bar{\cal{q}}_{i,j}-\bar{\cal{q}}_{i,j-1}}\right)\tag{40}\\
\end{align}
以上で求めた界面物理量をリーマンソルバに適用することで数値流束を求めることができます。
Roeリーマンソルバの2次元化
界面物理量が2次元化できたので、次はリーマンソルバを2次元化します。1次元のRoeリーマンソルバは次のように定義されました。
\tilde{f}_{i+\frac{1}{2}}&=\frac{1}{2}\left(a+\left|a\right|\right){}^L\! q_{i+\frac{1}{2}}+\frac{1}{2}\left(a-\left|a\right|\right){}^R\! q_{i+\frac{1}{2}}\\
\tilde{f}_{i-\frac{1}{2}}&=\frac{1}{2}\left(a+\left|a\right|\right){}^L\! q_{i-\frac{1}{2}}+\frac{1}{2}\left(a-\left|a\right|\right){}^R\! q_{i-\frac{1}{2}}\\
\tag{41}
\end{align}
2次元に拡張する場合、界面物理量\({}^L\! q_{i+\frac{1}{2}},{}^R\! q_{i+\frac{1}{2}}\)を2次元化すればよいので、次のように書けます。
- \(x\)成分
\tilde{f}_{i+\frac{1}{2},j}&=\frac{1}{2}\left(a_{x}+\left|a_{x}\right|\right){}^L\! q_{i+\frac{1}{2},j}+\frac{1}{2}\left(a_{x}-\left|a_{x}\right|\right){}^R\! q_{i+\frac{1}{2},j}\\
\tilde{f}_{i-\frac{1}{2},j}&=\frac{1}{2}\left(a_{x}+\left|a_{x}\right|\right){}^L\! q_{i-\frac{1}{2},j}+\frac{1}{2}\left(a_{x}-\left|a_{x}\right|\right){}^R\! q_{i-\frac{1}{2},j}\\
\tag{42}
\end{align}
- \(y\)成分
\tilde{f}_{i,j+\frac{1}{2}}&=\frac{1}{2}\left(a_{y}+\left|a_{y}\right|\right){}^L\! q_{i,j+\frac{1}{2}}+\frac{1}{2}\left(a_{y}-\left|a_{y}\right|\right){}^R\! q_{i,j+\frac{1}{2}}\\
\tilde{f}_{i,j-\frac{1}{2}}&=\frac{1}{2}\left(a_{y}+\left|a_{y}\right|\right){}^L\! q_{i,j-\frac{1}{2}}+\frac{1}{2}\left(a_{y}-\left|a_{y}\right|\right){}^R\! q_{i,j-\frac{1}{2}}\\
\tag{43}
\end{align}
以上で2次元数値流束が求まりました。これを式\((13)\)に代入することで、移流方程式を解くことが出来ます。
解析条件
ここまでで離散化式が得られらので、ここからは具体的な解析条件について記載します。
座標系・セル配置は次のように設定される2次元直交格子を考えます。まず5*5のメッシュ数を例として、セル平均値\(\bar{q}_{i,j}\)と数値流束\(\tilde{f}_{i+\frac{1}{2},j},\tilde{f}_{i-\frac{1}{2},j},\tilde{f}_{i,j+\frac{1}{2}},\tilde{f}_{i,j-\frac{1}{2}}\)の添え字の関係図を以下に示します。
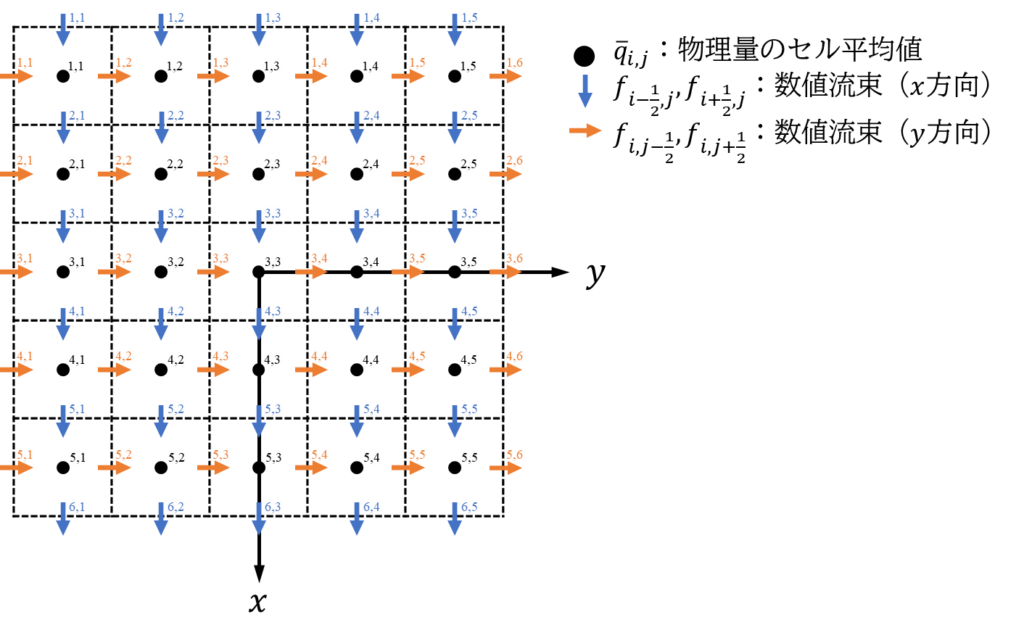
座標の原点は領域中心に設定しました。行列の行方向を\(x\)方向、列方向を\(y\)方向と対応付けるため、\(x\)軸は下向きに取っています。また、物理量のセル平均値\(\bar{q}_{i,j}\)が5*5のマトリクスであるのに対し、数値流束は界面で定義されるため、6*5、あるいは5*6のマトリクスで定義されることに注意しましょう。
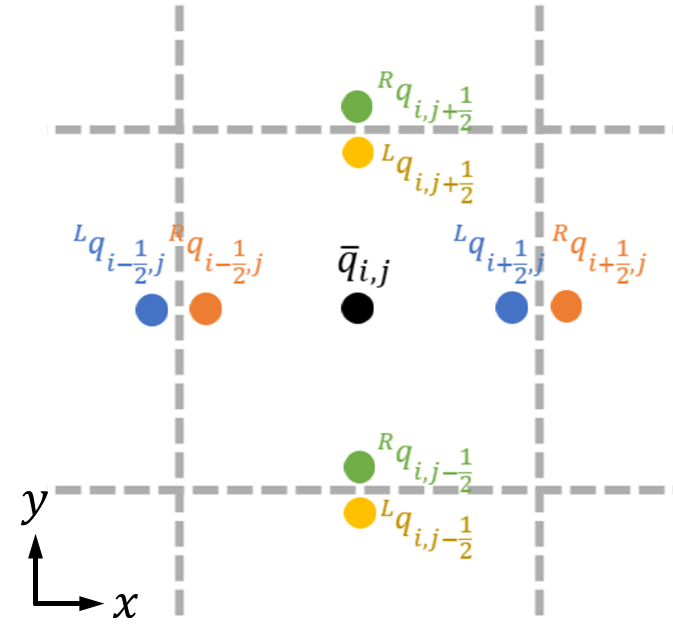
同様にセル平均値\(\bar{q}_{i,j}\)と界面物理量\({}^L\! q,{}^R\! q\)の関係は次のようになります。
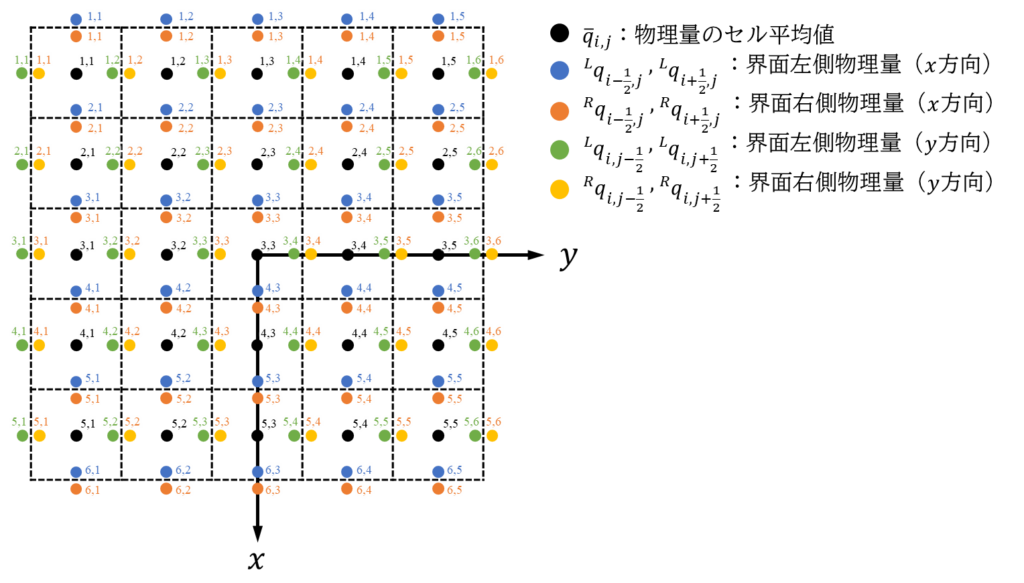
こちらも同様に、界面物理量は6*5、あるいは5*6のマトリクスで定義されることに注意しましょう。このように有限体積法による離散化では界面で定義される変数が無数にあるため、変数の位置関係がややこしくなるのは欠点かもしれません。
初期条件は、次式で定義される2次元矩形波を与えることとします。
\bar{\cal{q}}_{i,j}=
\begin{cases}
1 & \text{$ \frac{n_{x}}{2}-10 <i< \frac{n_{x}}{2}+10 \quadかつ \quad \frac{n_{y}}{2}-10 <j< \frac{n_{y}}{2}+10$} \\
0.1 & \text{$others$}
\end{cases}
\tag{44}
\end{align}
ここで\(n_{x},n_{y}\)は各方向のセル数を表します。
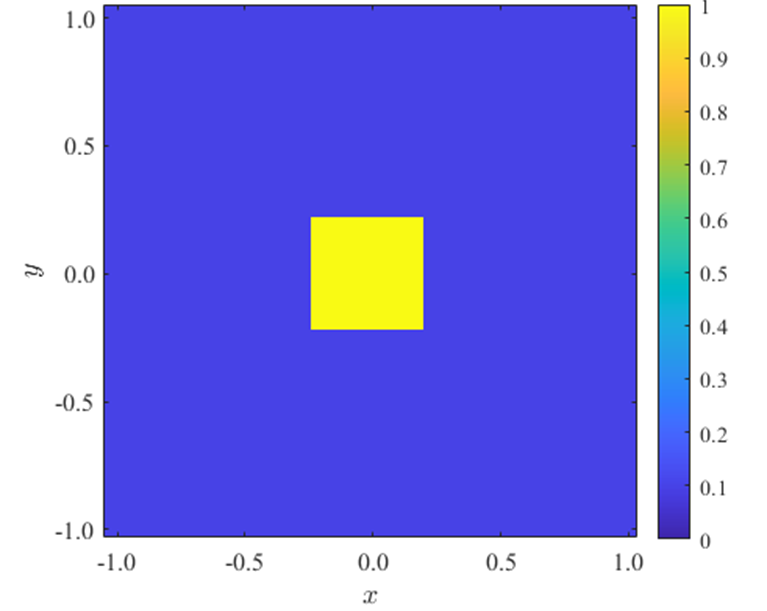
また、移流速度としては次の2ケースを考えます。
- ケース1:斜めに移動するケース\begin{align}
\left(
\begin{array}{c}
a_{x} \\
a_{y}
\end{array}
\right)
=
\left(
\begin{array}{c}
1 \\
1
\end{array}
\right)
\tag{45}
\end{align} - ケース2:反時計回りに回転運動するケース\begin{align}
\left(
\begin{array}{c}
a_{x} \\
a_{y}
\end{array}
\right)
=
\left(
\begin{array}{c}
-a \sin\left(\omega t\right)\\
a \cos\left(\omega t\right)\\
\end{array}
\right)
\tag{46}
\end{align}
周期的境界条件
1次元のときと同様に境界条件は周期的境界条件を適用します。1次元の周期的境界条件は、次のように与えられます。
\bar{\cal{q}}_{1}&=\bar{\cal{q}}_{n_{x}-3}\\
\bar{\cal{q}}_{2}&=\bar{\cal{q}}_{n_{x}-2}\\
\bar{\cal{q}}_{n_{x}-1}&=\bar{\cal{q}}_{3}\\
\bar{\cal{q}}_{n_{x}}&=\bar{\cal{q}}_{4}\\
\tag{47}
\end{align}


上式を2次元に拡張すると単純に次のように書けるでしょう。
- \(x\)成分
\bar{\cal{q}}_{1,j}&=\bar{\cal{q}}_{n_{x}-3,j}\\
\bar{\cal{q}}_{2,j}&=\bar{\cal{q}}_{n_{x}-2,j}\\
\bar{\cal{q}}_{n_{x}-1,j}&=\bar{\cal{q}}_{3,j}\\
\bar{\cal{q}}_{n_{x},j}&=\bar{\cal{q}}_{4,j}\\
\tag{48}
\end{align}
- \(y\)成分
\bar{\cal{q}}_{i,1}&=\bar{\cal{q}}_{i,n_{y}-3}\\
\bar{\cal{q}}_{i,2}&=\bar{\cal{q}}_{i,n_{y}-2}\\
\bar{\cal{q}}_{i,n_{y}-1}&=\bar{\cal{q}}_{i,3}\\
\bar{\cal{q}}_{i,n_{y}}&=\bar{\cal{q}}_{i,4}\\
\tag{49}
\end{align}
解析結果
それぞれのスキームについて、2種の移流速度が与える影響を評価します。まずは厳密解を示します。
- 厳密解
以降は数値解を順に示します。
- 1次風上差分法
1次元で確認した時と同様に、時間とともに界面がぼやけていく様子が確認できます。特に斜め方向への移流では、進行方向に対して垂直な方向の拡散が大きくなります。振動は生じませんが、厳密解からはほど遠いと言っていよいでしょう。
- 2次精度風上差分法(Beam warming法)
斜め方向への移流では、下流側で発生した振動が時間とともに増幅される様子が確認できます。一方、上流側では振動が生じず、1次精度と比較して波形が維持されていることが分かります。これは1次元で確認した時と同様の傾向です(過去記事参照)。
また、円運動の移流では、進行方向が切り替わった瞬間(上流と下流が入れ替わった瞬間)に、振動成分が消失する様子が確認できます。これは初期の不連続な波形により生じた振動が下流側に回ることで、数値拡散によってかき消されるためと考えられます。新たな上流側には初期条件のような不連続な分布は存在しないので、その後、振動が起こることはありません。最終的には1次精度と同程度の拡散具合で落ちついています。
上記の結果から、不連続波形が一方向に進行し続ける移流問題において、線形高次精度解法を使用することは、振動が継続的に増幅し、いずれは発散を招くことが分かります。
- Lax-Wendoroff法
- 空間3次精度・時間2次精度
- TVD法:minmod limiter
minmod limiterの場合、ここまでに記載した線形解法と比較して波形の維持性能が飛躍的に向上していることが分かります。しかしながら、依然として数値粘性自体は残っており、斜め方向への移流に関しては、その影響が顕著になってしまっています。
- TVD法:superbee limiter
1次元の場合、superbee limiterは高い波形の保存性を有していました(過去記事参照)。しかしながら2次元に拡張した場合、確かに数値粘性はほとんど見られませんが、鋭いピーク・振動が目立つようになってしまいました。これは移流によって生じた数値粘性をsuperbee limiterが強調してしまうためと考えられます。特に斜め方向への移流では、トゲのように鋭いピークが発生し、非物理的な解となってしまいました。
斜めの移流が数値拡散を招く理由
上記の解析結果より、斜め方向への移流はその垂直方向に大きな数値拡散を引き起こす傾向があることが分かりました。これについて、離散化誤差の観点からもう少し深堀しておきましょう。
2次元移流方程式は次式にて与えられました。(式\((1)\))
\frac{\partial q}{\partial t}+a_{x}\frac{\partial q}{\partial x}+a_{y}\frac{\partial q}{\partial y}= 0\tag{1}
\end{align}
上式について斜め方向の移流を想定し、\(a_x\geq 0,a_y\geq0\)とした時、時間1次・空間1次精度で離散化された移流方程式は次式にて与えられます。
\frac{\bar{q}_{i,j}^{n+1}-\bar{q}_{i,j}^{n}}{\Delta t}+a_{x}\frac{\bar{q}_{i,j}^{n}-\bar{q}_{i-1,j}^{n}}{\Delta x}+a_{y}\frac{ \bar{q}_{i,j}^{n}-\bar{q}_{i,j-1}^{n}}{\Delta y}= 0
\tag{50}
\end{align}
式\((40),(41)\)より数値流束の各成分は次のように計算されます。
- \(x\)成分
\tilde{f}_{i+\frac{1}{2},j}&=\frac{1}{2}\left(a_{x}+\left|a_{x}\right|\right){}^L\! q_{i+\frac{1}{2},j}+\frac{1}{2}\left(a_{x}-\left|a_{x}\right|\right){}^R\! q_{i+\frac{1}{2},j}=a_{x}{}^L\! q_{i+\frac{1}{2},j}\\
\tilde{f}_{i-\frac{1}{2},j}&=\frac{1}{2}\left(a_{x}+\left|a_{x}\right|\right){}^L\! q_{i-\frac{1}{2},j}+\frac{1}{2}\left(a_{x}-\left|a_{x}\right|\right){}^R\! q_{i-\frac{1}{2},j}=a_{x}{}^L\! q_{i-\frac{1}{2},j}\\
\tag{a1}
\end{align}
- \(y\)成分
\tilde{f}_{i,j+\frac{1}{2}}&=\frac{1}{2}\left(a_{y}+\left|a_{y}\right|\right){}^L\! q_{i,j+\frac{1}{2}}+\frac{1}{2}\left(a_{y}-\left|a_{y}\right|\right){}^R\! q_{i,j+\frac{1}{2}}=a_{y}{}^L\! q_{i,j+\frac{1}{2}}\\
\tilde{f}_{i,j-\frac{1}{2}}&=\frac{1}{2}\left(a_{y}+\left|a_{y}\right|\right){}^L\! q_{i,j-\frac{1}{2}}+\frac{1}{2}\left(a_{y}-\left|a_{y}\right|\right){}^R\! q_{i,j-\frac{1}{2}}=a_{y}{}^L\! q_{i,j-\frac{1}{2}}\\
\tag{a2}
\end{align}
ここで、空間1次精度を考える場合、次式が成り立ちます。(過去記事参照)
{}^L\! q_{i+\frac{1}{2},j}&=\bar{q}_{i,j}\\
{}^L\! q_{i-\frac{1}{2},j}&=\bar{q}_{i-1,j}\\
{}^L\! q_{i,j+\frac{1}{2}}&=\bar{q}_{i,j}\\
{}^L\! q_{i,j-\frac{1}{2}}&=\bar{q}_{i,j-1}\\
\tag{a3}
\end{align}
これらを式\((a1),(a2)\)に代入すると、次のような1次精度風上差分法が得られます。
- \(x\)成分
\tilde{f}_{i+\frac{1}{2},j}&=a_{x}{}^L\! q_{i+\frac{1}{2},j}=a_{x}\bar{q}_{i,j}\\
\tilde{f}_{i-\frac{1}{2},j}&=a_{x}{}^L\! q_{i-\frac{1}{2},j}=a_{x}\bar{q}_{i-1,j}\\
\tag{a4}
\end{align}
- \(y\)成分
\tilde{f}_{i,j+\frac{1}{2}}&=a_{y}{}^L\! q_{i,j+\frac{1}{2}}=a_{y}\bar{q}_{i,j}\\
\tilde{f}_{i,j-\frac{1}{2}}&=a_{y}{}^L\! q_{i,j-\frac{1}{2}}=a_{y}\bar{q}_{i,j-1}\\
\tag{a5}
\end{align}
これらを離散化された移流方程式(式\((11)\))に代入すると、次のセル平均値\(\bar{q}_{i,j}\)で表された移流方程式が得られます。
&\frac{\bar{q}_{i,j}^{n+1}-\bar{q}_{i,j}^{n}}{\Delta t}+\frac{ f_{i+\frac{1}{2},j}-f_{i-\frac{1}{2},j}}{\Delta x}+\frac{ f_{i,j+\frac{1}{2}}-f_{i,j-\frac{1}{2}}}{\Delta y}= 0\\
&\quad\quad\quad \Leftrightarrow
\frac{\bar{q}_{i,j}^{n+1}-\bar{q}_{i,j}^{n}}{\Delta t}+a_{x}\frac{\bar{q}_{i,j}^{n}-\bar{q}_{i-1,j}^{n}}{\Delta x}+a_{y}\frac{ \bar{q}_{i,j}^{n}-\bar{q}_{i,j-1}^{n}}{\Delta y}= 0
\tag{a6}
\end{align}
式\((1)\)は厳密ですが、式\((50)\)は離散化による近似式なので、当然、離散化誤差を含みます。この誤差について調べます。
\(\bar{q}_{i-1,j}^{n}=\bar{q}^{n}\left(x-\Delta x,y\right)\)について\(x\)の周りで2次の項までテイラー展開します。
\bar{q}^{n}\left(x-\Delta x,y\right)&= \bar{q}^{n}\left(x,y\right)+\frac{\partial \bar{q}^{n}}{\partial x}\left(-\Delta x\right)+\frac{1}{2}\frac{\partial ^2\bar{q}^{n}}{\partial x^2}\left(-\Delta x\right)^2+O\left(\left(-\Delta x\right)^3\right)\\
&= \bar{q}^{n}\left(x,y\right)-\frac{\partial \bar{q}^{n}}{\partial x}\left(\Delta x\right)+\frac{1}{2}\frac{\partial ^2\bar{q}^{n}}{\partial x^2}\left(\Delta x\right)^2+O\left(\left(\Delta x\right)^3\right)\tag{51}
\end{align}
1次精度風上差分法としてまとめると
&\frac{\bar{q}^{n}\left(x,y\right)-\bar{q}^{n}\left(x-\Delta x,y\right)}{\Delta x}=\frac{\partial \bar{q}^{n}}{\partial x} -\frac{1}{2}\frac{\partial ^2\bar{q}^{n}}{\partial x^2}\left(\Delta x\right)+O\left(\left(\Delta x\right)^2\right)\\
&\Leftrightarrow
\frac{\bar{q}_{i,j}^{n}-\bar{q}_{i-1,j}^{n}}{\Delta x}=\frac{\partial \bar{q}^{n}}{\partial x}-\frac{1}{2}\frac{\partial ^2\bar{q}^{n}}{\partial x^2}\left(\Delta x\right)+O\left(\left(\Delta x\right)^2\right)
\tag{52}
\end{align}
上式は「1次精度風上差分法による近似は、拡散項\(\frac{\partial ^2\bar{q}^{n}}{\partial x^2}\)に比例する1次の誤差(右辺第二項)を有している」ことを示しています。同様に\(y\)方向については次式が得られます。
\frac{\bar{q}_{i,j}^{n}-\bar{q}_{i,j-1}^{n}}{\Delta y}&=\frac{\partial \bar{q}^{n}}{\partial y}-\frac{1}{2}\frac{\partial ^2\bar{q}^{n}}{\partial y^2}\left(\Delta y\right)+O\left(\left(\Delta y\right)^2\right)
\tag{53}
\end{align}
さらに時間微分についても同様に考えます。\(\bar{q}_{i,j}^{n+1}=\bar{q}\left(t+\Delta t\right)\)について\(t\)の周りで2次の項までテイラー展開します。
&\bar{q}\left(t+\Delta t\right)= \bar{q}\left(t\right)+\frac{\partial \bar{q}}{\partial t}\Delta t+\frac{1}{2}\frac{\partial ^2\bar{q}}{\partial t^2}\left(\Delta t\right)^2+O\left(\left(\Delta t\right)^3\right)\\
&\Leftrightarrow \frac{\bar{q}\left(t+\Delta t\right)-\bar{q}\left(t\right)}{\Delta t}=\frac{\partial \bar{q}}{\partial t} +\frac{1}{2}\frac{\partial ^2\bar{q}}{\partial t^2}\left(\Delta t\right)+O\left(\left(\Delta t\right)^2\right)\\
&\Leftrightarrow \frac{\bar{q}_{i,j}^{n+1}-\bar{q}_{i,j}^{n}}{\Delta t}= \frac{\partial \bar{q}}{\partial t} +\frac{1}{2}\frac{\partial ^2\bar{q}}{\partial t^2}\left(\Delta t\right)+O\left(\left(\Delta t\right)^2\right)
\tag{54}
\end{align}
以上\((52)\sim(54)\)を\((50)\)に代入します。
& \frac{\partial \bar{q}}{\partial t} +\frac{1}{2}\frac{\partial ^2\bar{q}}{\partial t^2}\left(\Delta t\right)+O\left(\left(\Delta t\right)^2\right)\\
&\quad+a_{x}\left\{\frac{\partial \bar{q}^{n}}{\partial x}-\frac{1}{2}\frac{\partial ^2\bar{q}^{n}}{\partial x^2}\left(\Delta x\right)+O\left(\left(\Delta x\right)^2\right)\right\}\\
&\quad\quad+a_{y}\left\{\frac{\partial \bar{q}^{n}}{\partial y}-\frac{1}{2}\frac{\partial ^2\bar{q}^{n}}{\partial y^2}\left(\Delta y\right)+O\left(\left(\Delta y\right)^2\right)\right\}= 0\\
&\Leftrightarrow
\frac{\partial \bar{q}}{\partial t} +a_{x}\frac{\partial \bar{q}}{\partial x}+a_{y}\frac{\partial \bar{q}}{\partial y}\\
&\quad\quad\quad+\frac{1}{2}\frac{\partial ^2\bar{q}}{\partial t^2}\left(\Delta t\right)-a_{x}\frac{1}{2}\frac{\partial ^2\bar{q}}{\partial x^2}\left(\Delta x\right)-a_{y}\frac{1}{2}\frac{\partial ^2\bar{q}}{\partial y^2}\left(\Delta y\right)\\
&\quad\quad\quad\quad\quad\quad+O\left(\left(\Delta t\right)^2\right)+O\left(\left(\Delta x\right)^2\right)+O\left(\left(\Delta y\right)^2\right)= 0
\tag{55}
\end{align}
上式1行目は式\((1)\)と一致しており、線形移流方程式そのものです。また、2、3行目は離散化誤差を表します。特に2行目には\(x,y\)方向の空間2階微分に比例した1次の誤差が存在しています。
つまり、上式は「離散化式\((50)\)を解くことは、元の移流方程式に拡散成分となる空間2階微分に比例する誤差を付け足した式を解くことに等しい」ということを意味しています。さらにこの誤差は\(x,y\)の2方向分存在するため、1次元の時と比較して、数値粘性が大きくなってしまっていることが分かります。3次元で考えると、さらに大きな誤差が生じるでしょう。これが前節までに斜め方向で大きな拡散が生じた原因です。
したがって、CFDにおいてメッシングはできるだけ流れ方向に沿って行うべきであり、流れを斜めに横切るようなメッシングは行うべきではありません。とはいえ流れがどの方向に生じるかは解析してみないとわからない部分もありますし、そもそも流れは場所ごとに時々刻々と変化するものなので、それに沿うようなメッシュなんてほぼ切れないのですけども…。
MATLABコード
以下に今回使用したMATLABコードを記載します。
% 初期化
clearvars;
% パラメーター
i_max = 100; % 格子セル数
j_max = 100; % 格子セル数
XL = -1.0; % 計算領域左端の座標
XR = 1.0; % 計算領域右端の座標
YL = XL; % 計算領域左端の座標
YR = XR; % 計算領域右端の座標
tstop = 2.0; % 計算停止時刻
N_Ghost = 2; % 周期境界条件用のゴーストセルの数。
% 配列定義
i = 0; % セル番号; (i番目セルの左境界の番号はi、右辺境界の番号はi+1とする)
x = zeros(i_max + 1, j_max + 1); % セル境界の座標
y = zeros(i_max + 1, j_max + 1); % セル境界の座標
u = zeros(i_max, j_max); % セル平均値 (数値解)
ue = zeros(i_max, j_max); % セル平均値 (厳密解)
ulx = zeros(i_max + 1, j_max); % x方向のセル境界左側の変数値
urx = zeros(i_max + 1, j_max); % x方向のセル境界右側の変数値
uly = zeros(i_max, j_max + 1); % y方向のセル境界左側の変数値
ury = zeros(i_max, j_max + 1); % y方向のセル境界右側の変数値
fx = zeros(i_max + 1, j_max); % セル境界の流束
fy = zeros(i_max, j_max + 1); % セル境界の流束
n = 0; % 時間ステップ
t = 0; % 計算時間
% 移流速度の定義
ax = 1;% 線形移流方程式の移流速度
ay = 1;% 線形移流方程式の移流速度
% 円運動の定義
rt = 0.5; % 円運動半径
theta0 = 0; % 初期位相
t_cycle = 1;% 周期
omega = 2.*pi/t_cycle; % 角速度
a = rt*omega; % 速度
% 移流速度の切り替え
sw_v = 1; % 斜め方向への移流:1、 円運動の移流:2
% スキームを選択する。
%method = 'exact';
method = '1st order UDS';
%method = 'Lax-Wendroff method';
%method = '3rd-S and 2nd-T';
%method = 'minmod-limiter';
%method = 'vanLeer-limiter';
%method = 'vanAlbada-limiter';
%method = 'superbee-limiter';
%method = '2nd order UDS';
% 格子間隔 計算領域外に二つずつ余分なセルを準備(プラス側マイナス側で2ずつ。)。周期的境界条件向けの設定
dx = (XR - XL) / (i_max - 4.0);
dy = (YR - YL) / (j_max - 4.0);
% 時間刻み
dt = 0.2 * dx;
% 計算領域外(左側)の2セルも考慮した座標を振る。
x(1,:) = XL - 2.0 * dx;
y(:,1) = YL - 2.0 * dy;
% 計算格子,時間刻み,初期条件を設定する
[x,y,u] = initc(i_max, j_max, x, y, dx, dy, u);
% メインループ
while t <= tstop
% 時間発展
n = n + 1;
t = t + dt;
% 速度更新
if sw_v == 1
xc = ax * t;% 厳密解計算用
yc = ay * t;% 厳密解計算用
elseif sw_v == 2
theta = theta0 + omega * t;
x0 = -rt;
y0 = 0;
xc = rt * cos(theta)+x0;% 厳密解計算用
yc = rt * sin(theta)+y0;% 厳密解計算用
ax = -a * sin(theta);
ay = a * cos(theta);
end
% 空間再構築
switch method
case '1st order UDS'
[ulx, urx] = reconstruction_uds_x(i_max, j_max, u, ulx, urx);
[uly, ury] = reconstruction_uds_y(i_max, j_max, u, uly, ury);
case 'Lax-Wendroff method'
[ulx, urx] = reconstruction_lw_x(i_max,j_max, u, ulx, urx, ax, dt, dx);
[uly, ury] = reconstruction_lw_y(i_max,j_max, u, uly, ury, ay, dt, dy);
case '3rd-S and 2nd-T'
[ulx, urx] = reconstruction_s3t2_x(i_max,j_max, u, ulx, urx, ax, dt, dx);
[uly, ury] = reconstruction_s3t2_y(i_max,j_max, u, uly, ury, ay, dt, dy);
case 'minmod-limiter'
[ulx, urx] = reconstruction_minmod_x(i_max,j_max, u, ulx, urx, ax, dt, dx);
[uly, ury] = reconstruction_minmod_y(i_max,j_max, u, uly, ury, ay, dt, dy);
case 'vanLeer-limiter'
[ulx, urx] = reconstruction_vanLeer_x(i_max, j_max, u, ulx, urx, ax, dt, dx);
[uly, ury] = reconstruction_vanLeer_y(i_max, j_max, u, uly, ury, ay, dt, dy);
case 'vanAlbada-limiter'
[ulx, urx] = reconstruction_vanAlbada_x(i_max, j_max, u, ulx, urx, ax, dt, dx);
[uly, ury] = reconstruction_vanAlbada_y(i_max, j_max, u, uly, ury, ay, dt, dy);
case 'superbee-limiter'
[ulx, urx] = reconstruction_superbee_x(i_max, j_max, u, ulx, urx, ax, dt, dx);
[uly, ury] = reconstruction_superbee_y(i_max, j_max, u, uly, ury, ay, dt, dy);
case '2nd order UDS'% = Beam warming法
[ulx, urx] = reconstruction_2nd_uds_x(i_max, j_max, u, ulx, urx, ax, dt, dx);
[uly, ury] = reconstruction_2nd_uds_y(i_max, j_max, u, uly, ury, ay, dt, dy);
end
% リーマンソルバー
fx = riemann_roe_x(i_max, j_max, fx, ax, ulx, urx); % 流束を計算する
fy = riemann_roe_y(i_max, j_max, fy, ay, uly, ury); % 流束を計算する
% 時間積分
u = update(i_max, j_max, u, dt, dx, dy, fx, fy);
% 境界条件
u = bc(i_max,j_max, u);
% 厳密解
if method == "exact"
u = exact(i_max, j_max, ue, xc, yc, ax, ay, t, dx, dy);
end
% 出力
fprintf("n=%d, t=%f \n", n, t);
% 動画保存
if n == 1
plotconfig(x(1 : end - 1,1 : end - 1),y(1 : end - 1,1 : end - 1), u, t, method)
filename = [method, ', sw_v = ', num2str(sw_v), '.mp4'];
v = VideoWriter(filename, 'MPEG-4');
v.FrameRate = 40;
open(v);
else
plotconfig(x(1 : end - 1,1 : end - 1),y(1 : end - 1,1 : end - 1), u, t, method)
frame = getframe(gcf);
writeVideo(v,frame);
end
end
% 動画ファイルを閉じる
close(v);
%% 以下ローカル関数
function [x,y,u] = initc(i_max, j_max, x, y, dx, dy, u)
for i = 2 : i_max + 1
for j = 1 : j_max + 1
x(i,j) = x(i - 1,j) + dx;% 格子点の座標
end
end
for i = 1 : i_max + 1
for j = 2 : j_max + 1
y(i,j) = y(i ,j - 1) + dy;% 格子点の座標
end
end
% 矩形波分布の定義
for i = 1 : i_max
for j = 1 : j_max
u(i,j) = 0.1;
end
end
for i = i_max / 2 - 10 : i_max / 2 + 10
for j = j_max / 2 - 10 : j_max / 2 + 10
u(i,j) = 1.0;
end
end
end
function [ue] = exact(i_max, j_max, ue, xc, yc, ax, ay, t, dx, dy)
% 波形の左端
xl = xc - dx * 10;% 中央に対して10要素だけマイナスに移動した位置
yl = yc - dy * 10;% 中央に対して10要素だけマイナスに移動した位置
% 周期境界条件
if xl > 1.0
xl = -2.0 + xl;
end
if yl > 1.0
yl = -2.0 + yl;
end
if xl < -1.0
xl = 2.0 + xl;
end
if yl < -1.0
yl = 2.0 + yl;
end
% 波形の右端
xr = xc + dx * 10;% 中央に対して10要素だけプラスに移動した位置
yr = yc + dy * 10;% 中央に対して10要素だけプラスに移動した位置
% 周期境界条件
if xr > 1.0
xr = -2.0 + xr;
end
if yr > 1.0
yr = -2.0 + yr;
end
if xr < -1.0
xr = 2.0 + xr;
end
if yr < -1.0
yr = 2.0 + yr;
end
% 境界に接していない場合
if xl <= xr
for i = 1 : i_max
for j = 1 : j_max
ue(i,j) = 0.1;
if dx * (i - i_max / 2) >= xl && dx * (i - i_max / 2) <= xr ...
&& dy * (j - j_max / 2) >= yl && dy * (j - j_max / 2) <= yr
ue(i,j) = 1.0;
end
end
end
end
% x境界にのみ接した場合
if xl >= xr && yl <= yr
for i = 1 : i_max
for j = 1 : j_max
ue(i,j) = 0.1;
if dx * (i - i_max / 2) >= xl || dx * (i - i_max / 2) <= xr
if dy * (j - j_max / 2) >= yl && dy * (j - j_max / 2) <= yr
ue(i,j) = 1.0;
end
end
end
end
end
% y境界にのみ接した場合
if xl <= xr && yl >= yr
for i = 1 : i_max
for j = 1 : j_max
ue(i,j) = 0.1;
if dx * (i - i_max / 2) >= xl && dx * (i - i_max / 2) <= xr
if dy * (j - j_max / 2) >= yl || dy * (j - j_max / 2) <= yr
ue(i,j) = 1.0;
end
end
end
end
end
% x境界とy境界の両方に接した場合
if xl >= xr && yl >= yr
for i = 1 : i_max
for j = 1 : j_max
ue(i,j) = 0.1;
if dx * (i - i_max / 2) >= xl || dx * (i - i_max / 2) <= xr
if dy * (j - j_max / 2) >= yl || dy * (j - j_max / 2) <= yr
ue(i,j) = 1.0;
end
end
end
end
end
end
function [ulx, urx] = reconstruction_uds_x(i_max, j_max, u, ulx, urx)
for i = 2 : i_max - 2% ゴーストセルのセル界面(端二つ)は計算しない
for j = 2 : j_max - 2 % ゴーストセルのセル界面(端二つ)は計算しない
ulx(i + 1,j) = u(i,j); % セル境界(i+1/2)左側の値
urx(i + 1,j) = u(i + 1,j); % セル境界(i+1/2)右側の値
end
end
end
function [uly, ury] = reconstruction_uds_y(i_max, j_max, u, uly, ury)
for i = 2 : i_max - 2 % ゴーストセルのセル界面(端二つ)は計算しない
for j = 2 : j_max - 2 % ゴーストセルのセル界面(端二つ)は計算しない
uly(i,j + 1) = u(i,j); % セル境界(i+1/2)左側の値
ury(i,j + 1) = u(i,j + 1); % セル境界(i+1/2)右側の値
end
end
end
function [ulx, urx] = reconstruction_lw_x(i_max, j_max, u, ulx, urx, ax, dt, dx)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
alpha_12 = ax;
deltaL = 0.5 * (u(i + 1,j) - u(i,j));
deltaR = 0.5 * (u(i + 1,j) - u(i,j));
ulx(i + 1,j) = u(i,j) + (1.0 - alpha_12 * dt / dx) * deltaL; % セル境界(i+1/2)左側の値
urx(i + 1,j) = u(i + 1,j) - (1.0 + alpha_12*dt / dx) * deltaR; % セル境界(i+1/2)右側の値
end
end
end
function [uly, ury] = reconstruction_lw_y(i_max, j_max, u, uly, ury, ay, dt, dy)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
alpha_12 = ay;
deltaL = 0.5 * (u(i,j + 1) - u(i,j));
deltaR = 0.5 * (u(i,j + 1) - u(i,j));
uly(i,j + 1) = u(i,j) + (1.0 - alpha_12 * dt / dy) * deltaL; % セル境界(i+1/2)左側の値
ury(i,j + 1) = u(i,j + 1) - (1.0 + alpha_12*dt / dy) * deltaR; % セル境界(i+1/2)右側の値
end
end
end
function [ulx, urx] = reconstruction_s3t2_x(i_max, j_max, u, ulx, urx, ax, dt, dx)
eps = 1;
kappa = 1 / 3;
for i = 2 : i_max - 2
for j = 2 : j_max - 2
alpha_12 = ax;
deltaL = eps * (0.25 * (1 - kappa) * (u(i,j) - u(i - 1,j))...
+ 0.25 * (1 + kappa) * (u(i + 1,j) - u(i,j)) );
deltaR = eps *(- 0.25 * (1 + kappa) * (u(i + 1,j) - u(i,j))...
- 0.25 * (1 - kappa) * (u(i + 2,j) - u(i + 1,j)));
ulx(i + 1,j) = u(i,j) + (1.0 - alpha_12 * dt / dx) * deltaL; % セル境界(i+1/2)左側の値
urx(i + 1,j) = u(i + 1,j) - (1.0 + alpha_12*dt / dx) * deltaR; % セル境界(i+1/2)右側の値
end
end
end
function [uly, ury] = reconstruction_s3t2_y(i_max, j_max, u, uly, ury, ay, dt, dy)
eps = 1;
kappa = 1 / 3;
for i = 2 : i_max - 2
for j = 2 : j_max - 2
alpha_12 = ay;
deltaL = eps * (0.25 * (1 - kappa) * (u(i,j) - u(i,j - 1))...
+ 0.25 * (1 + kappa) * (u(i,j + 1) - u(i,j)) );
deltaR = eps *(- 0.25 * (1 + kappa) * (u(i,j + 1) - u(i,j))...
- 0.25 * (1 - kappa) * (u(i,j + 2) - u(i,j + 1)));
uly(i,j + 1) = u(i,j) + (1.0 - alpha_12 * dt / dy) * deltaL; % セル境界(i+1/2)左側の値
ury(i,j + 1) = u(i,j + 1) - (1.0 + alpha_12*dt / dy) * deltaR; % セル境界(i+1/2)右側の値
end
end
end
function [fx] = riemann_roe_x(i_max, j_max, fx, ax, ulx, urx) % 流束を計算する
for i = 3 : i_max - 1 % ゴーストセルではないセルの流入出の流束の範囲で計算。
for j = 3 : j_max - 1 % ゴーストセルではないセルの流入出の流束の範囲で計算。
fx(i,j) = 1.0 / 2.0 * (ax * ulx(i,j) + ax * urx(i,j)) - 1.0 / 2.0 * abs(ax) * (urx(i,j) - ulx(i,j));
end
end
end
function [fy] = riemann_roe_y(i_max, j_max, fy, ay, uly, ury) % 流束を計算する
for i = 3 : i_max - 1
for j = 3 : j_max - 1
fy(i,j) = 1.0 / 2.0 * (ay * uly(i,j) + ay * ury(i,j)) - 1.0 / 2.0 * abs(ay) * (ury(i,j) - uly(i,j));
end
end
end
function [u] = update(i_max, j_max, u, dt, dx, dy, fx, fy)
for i = 3 : i_max - 2 % ゴーストセルを除いた範囲で計算
for j = 3 : j_max - 2
u(i,j) = u(i,j) - dt / dx * (fx(i + 1,j) - fx(i,j))- dt / dy * (fy(i ,j+ 1) - fy(i,j));% 更新する
end
end
end
function [u] = bc(i_max,j_max, u) % 周期境界条件
u(1,:) = u(i_max - 3,:); % 計算領域左端の境界条件
u(2,:) = u(i_max - 2,:); % 計算領域左端の境界条件
u(i_max - 1,:) = u(3,:); % 計算領域右端の境界条件
u(i_max,:) = u(4,:); % 計算領域右端の境界条件
u(:,1) = u(:,j_max - 3); % 計算領域左端の境界条件
u(:,2) = u(:,j_max - 2); % 計算領域左端の境界条件
u(:,j_max - 1) = u(:,3); % 計算領域右端の境界条件
u(:,j_max) = u(:,4); % 計算領域右端の境界条件
end
function [] = plotconfig(x, y, u, t, method)
% レンジの決定
xmin = min(x(:,1));
xmax = max(x(:,1));
ymin = min(y(1,:));
ymax = max(y(1,:));
% imagesc の第1, 第2引数に [xmin, xmax], [ymin, ymax] を指定
imagesc([xmin, xmax], [ymin, ymax], imrotate(u, 90), [0, 1]);
colorbar;
title(['time = ', num2str(t, '%.3f')]);
% 背景を白に
fig=gcf;
fig.Color='white';
% 軸ラベルやフォント設定
xlabel('$$x$$','Interpreter','latex','FontSize',12);
ylabel('$$y$$','Interpreter','latex','FontSize',12);
set(gca, 'FontName','Times New Roman', 'FontSize',12);
% 軸のアスペクト比・表示範囲の設定
axis('equal');
axis('tight');
% Y軸のカスタム目盛りを設定
ytick_values = linspace(-1.0, 1.0, 5); % Y軸の目盛り値
ytick_labels = flip(ytick_values); % ラベルを反転
set(gca, 'YTick', ytick_values, 'YTickLabel', arrayfun(@(v) sprintf('%.1f', v), ytick_labels, 'UniformOutput', false));
% 'TickLabelFormat'を利用してX軸の桁数を指定
ax = gca;
ax.XAxis.TickLabelFormat = '%.1f'; % X軸の桁数を小数点以下2桁に設定
% 右下に method 名をテキストボックスで表示
%text(xmax-0.05, ymax-0.15, 'exact', ...
text(xmax-0.05, ymax-0.15, method, ...
'FontSize', 12, ...
'FontName', 'Times New Roman', ...
'HorizontalAlignment', 'right', ... % 右揃え
'VerticalAlignment', 'top', ... % 上揃え
'BackgroundColor', 'none', ... % 背景を白に
'EdgeColor', 'none'); % 枠線なし
end
function [ulx, urx] = reconstruction_minmod_x(i_max,j_max, u, ulx, urx, ax, dt, dx)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
% セル境界(i+1/2)の左側の勾配比
rL = (u(i,j) - u(i - 1,j)) / (u(i + 1,j) - u(i,j) + signfunc(u(i + 1,j) - u(i,j)) * 1.0e-5);% ゼロ割が発生しないように微小量を足す。
% セル境界(i+1/2)の右側の勾配比
rR = (u(i + 2,j) - u(i + 1,j)) / (u(i + 1,j) - u(i,j) + signfunc(u(i + 1,j) - u(i,j)) * 1.0e-5);
phiL = minmod(rL);
phiR = minmod(rR);
deltaL = 0.5 * (u(i + 1,j) - u(i,j));
deltaR = 0.5 * (u(i + 1,j) - u(i,j));
alpha_12 = ax;
ulx(i + 1,j) = u(i,j) + (1.0 - alpha_12 * dt / dx) * phiL * deltaL;% セル境界(i+1/2)左側の値
urx(i + 1,j) = u(i + 1,j) - (1.0 + alpha_12 * dt / dx) * phiR * deltaR;% セル境界(i+1/2)右側の値
end
end
end
function [uly, ury] = reconstruction_minmod_y(i_max,j_max, u, uly, ury, ay, dt, dy)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
% セル境界(i+1/2)の左側の勾配比
rL = (u(i,j) - u(i,j - 1)) / (u(i,j + 1) - u(i,j) + signfunc(u(i,j + 1) - u(i,j)) * 1.0e-5);% ゼロ割が発生しないように微小量を足す。
% セル境界(i+1/2)の右側の勾配比
rR = (u(i,j + 2) - u(i,j + 1)) / (u(i,j + 1) - u(i,j) + signfunc(u(i,j + 1) - u(i,j)) * 1.0e-5);
phiL = minmod(rL);
phiR = minmod(rR);
deltaL = 0.5 * (u(i,j + 1) - u(i,j));
deltaR = 0.5 * (u(i,j + 1) - u(i,j));
alpha_12 = ay;
uly(i,j + 1) = u(i,j) + (1.0 - alpha_12 * dt / dy) * phiL * deltaL;% セル境界(i+1/2)左側の値
ury(i,j + 1) = u(i,j + 1) - (1.0 + alpha_12 * dt / dy) * phiR * deltaR;% セル境界(i+1/2)右側の値
end
end
end
function [a] = minmod(x)
a = max(0.0, min(1.0, x));
end
function [a] = signfunc(x)
if x >= 0
a = 1;
else
a = -1;
end
end
function [ulx, urx] = reconstruction_vanLeer_x(i_max, j_max, u, ulx, urx, ax, dt, dx)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
% セル境界(i+1/2)の左側の勾配比
rL = (u(i,j) - u(i - 1,j)) / (u(i + 1,j) - u(i,j) + signfunc(u(i + 1,j) - u(i,j)) * 1.0e-5);
% セル境界(i+1/2)の右側の勾配比
rR = (u(i + 2,j) - u(i + 1,j)) / (u(i + 1,j) - u(i,j) + signfunc(u(i + 1,j) - u(i,j)) * 1.0e-5);
phiL = vanLeer(rL);
phiR = vanLeer(rR);
deltaL = 0.5 * (u(i + 1,j) - u(i,j));
deltaR = 0.5 * (u(i + 1,j) - u(i,j));
alpha_12 = ax;
ulx(i + 1,j) = u(i,j) + (1.0 - alpha_12 * dt / dx) * phiL * deltaL;% セル境界(i+1/2)左側の値
urx(i + 1,j) = u(i + 1,j) - (1.0 + alpha_12 * dt / dx) * phiR * deltaR;% セル境界(i+1/2)右側の値
end
end
end
function [uly, ury] = reconstruction_vanLeer_y(i_max, j_max, u, uly, ury, ay, dt, dy)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
% セル境界(i+1/2)の左側の勾配比
rL = (u(i,j) - u(i,j - 1)) / (u(i,j + 1) - u(i,j) + signfunc(u(i,j + 1) - u(i,j)) * 1.0e-5);
% セル境界(i+1/2)の右側の勾配比
rR = (u(i,j + 2) - u(i,j + 1)) / (u(i,j + 1) - u(i,j) + signfunc(u(i,j + 1) - u(i,j)) * 1.0e-5);
phiL = vanLeer(rL);
phiR = vanLeer(rR);
deltaL = 0.5 * (u(i,j + 1) - u(i,j));
deltaR = 0.5 * (u(i,j + 1) - u(i,j));
alpha_12 = ay;
uly(i,j + 1) = u(i,j) + (1.0 - alpha_12 * dt / dy) * phiL * deltaL;% セル境界(i+1/2)左側の値
ury(i,j + 1) = u(i,j + 1) - (1.0 + alpha_12 * dt / dy) * phiR * deltaR;% セル境界(i+1/2)右側の値
end
end
end
function [a] = vanLeer(x) % van Leer limiter
a = (x + abs(x)) / (1 + abs(x));
end
function [ul, ur] = reconstruction_vanAlbada(i_max, u, ul, ur, a, dt, dx)
for i = 2 : i_max - 2
% セル境界(i+1/2)の左側の勾配比
rL = (u(i) - u(i - 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);
% セル境界(i+1/2)の右側の勾配比
rR = (u(i + 2) - u(i + 1)) / (u(i + 1) - u(i) + signfunc(u(i + 1) - u(i)) * 1.0e-5);
phiL = vanAlbada(rL);
phiR = vanAlbada(rR);
deltaL = 0.5 * (u(i + 1) - u(i));
deltaR = 0.5 * (u(i + 1) - u(i));
alpha_12 = a;
ul(i + 1) = u(i) + (1.0 - alpha_12 * dt / dx) * phiL * deltaL; % セル境界(i+1/2)左側の値
ur(i + 1) = u(i + 1) - (1.0 + alpha_12 * dt / dx) * phiR * deltaR; % セル境界(i+1/2)右側の値
end
end
function [ulx, urx] = reconstruction_vanAlbada_x(i_max, j_max, u, ulx, urx, ax, dt, dx)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
% セル境界(i+1/2)の左側の勾配比
rL = (u(i,j) - u(i - 1,j)) / (u(i + 1,j) - u(i,j) + signfunc(u(i + 1,j) - u(i,j)) * 1.0e-5);
% セル境界(i+1/2)の右側の勾配比
rR = (u(i + 2,j) - u(i + 1,j)) / (u(i + 1,j) - u(i,j) + signfunc(u(i + 1,j) - u(i,j)) * 1.0e-5);
phiL = vanAlbada(rL);
phiR = vanAlbada(rR);
deltaL = 0.5 * (u(i + 1,j) - u(i,j));
deltaR = 0.5 * (u(i + 1,j) - u(i,j));
alpha_12 = ax;
ulx(i + 1,j) = u(i,j) + (1.0 - alpha_12 * dt / dx) * phiL * deltaL; % セル境界(i+1/2)左側の値
urx(i + 1,j) = u(i + 1,j) - (1.0 + alpha_12 * dt / dx) * phiR * deltaR; % セル境界(i+1/2)右側の値
end
end
end
function [uly, ury] = reconstruction_vanAlbada_y(i_max, j_max, u, uly, ury, ay, dt, dy)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
% セル境界(i+1/2)の左側の勾配比
rL = (u(i,j) - u(i,j - 1)) / (u(i,j + 1) - u(i,j) + signfunc(u(i,j + 1) - u(i,j)) * 1.0e-5);
% セル境界(i+1/2)の右側の勾配比
rR = (u(i,j + 2) - u(i,j + 1)) / (u(i,j + 1) - u(i,j) + signfunc(u(i,j + 1) - u(i,j)) * 1.0e-5);
phiL = vanAlbada(rL);
phiR = vanAlbada(rR);
deltaL = 0.5 * (u(i,j + 1) - u(i,j));
deltaR = 0.5 * (u(i,j + 1) - u(i,j));
alpha_12 = ay;
uly(i,j + 1) = u(i,j) + (1.0 - alpha_12 * dt / dy) * phiL * deltaL; % セル境界(i+1/2)左側の値
ury(i,j + 1) = u(i,j + 1) - (1.0 + alpha_12 * dt / dy) * phiR * deltaR; % セル境界(i+1/2)右側の値
end
end
end
function[a] = vanAlbada(x) % van Albada limiter
a = (x + x * x) / (1 + x * x);
end
function [ulx, urx] = reconstruction_superbee_x(i_max, j_max, u, ulx, urx, ax, dt, dx)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
% セル境界(i+1/2)の左側の勾配比
rL = (u(i,j) - u(i - 1,j)) / (u(i + 1,j) - u(i,j) + signfunc(u(i + 1,j) - u(i,j)) * 1.0e-5);
% セル境界(i+1/2)の右側の勾配比
rR = (u(i + 2,j) - u(i + 1,j)) / (u(i + 1,j) - u(i,j) + signfunc(u(i + 1,j) - u(i,j)) * 1.0e-5);
phiL = superbee(rL);
phiR = superbee(rR);
deltaL = 0.5 * (u(i + 1,j) - u(i,j));
deltaR = 0.5 * (u(i + 1,j) - u(i,j));
alpha_12 = ax;
ulx(i + 1,j) = u(i,j) + (1.0 - alpha_12 * dt / dx) * phiL * deltaL; % セル境界(i+1/2)左側の値
urx(i + 1,j) = u(i + 1,j) - (1.0 + alpha_12 * dt / dx) * phiR * deltaR; % セル境界(i+1/2)右側の値
end
end
end
function [uly, ury] = reconstruction_superbee_y(i_max, j_max, u, uly, ury, ay, dt, dy)
for i = 2 : i_max - 2
for j = 2 : j_max - 2
% セル境界(i+1/2)の左側の勾配比
rL = (u(i,j) - u(i,j - 1)) / (u(i,j + 1) - u(i,j) + signfunc(u(i,j + 1) - u(i,j)) * 1.0e-5);
% セル境界(i+1/2)の右側の勾配比
rR = (u(i,j + 2) - u(i,j + 1)) / (u(i,j + 1) - u(i,j) + signfunc(u(i,j + 1) - u(i,j)) * 1.0e-5);
phiL = superbee(rL);
phiR = superbee(rR);
deltaL = 0.5 * (u(i,j + 1) - u(i,j));
deltaR = 0.5 * (u(i,j + 1) - u(i,j));
alpha_12 = ay;
uly(i,j + 1) = u(i,j) + (1.0 - alpha_12 * dt / dy) * phiL * deltaL; % セル境界(i+1/2)左側の値
ury(i,j + 1) = u(i,j + 1) - (1.0 + alpha_12 * dt / dy) * phiR * deltaR; % セル境界(i+1/2)右側の値
end
end
end
function[a] = superbee(x)% Superbee limiter
a = max(max(0.0, min(1.0, 2.0 * x)), min(2.0, x));
end
function [ulx, urx] = reconstruction_2nd_uds_x(i_max, j_max, u, ulx, urx, ax, dt, dx)
eps = 1;
kappa = -1;
for i = 2 : i_max - 2
for j = 2 : j_max - 2
alpha_12 = ax;
deltaL = eps * (0.25 * (1 - kappa) * (u(i,j) - u(i - 1,j))...
+ 0.25 * (1 + kappa) * (u(i + 1,j) - u(i,j)) );
deltaR = eps *(- 0.25 * (1 + kappa) * (u(i + 1,j) - u(i,j))...
- 0.25 * (1 - kappa) * (u(i + 2,j) - u(i + 1,j)));
ulx(i + 1,j) = u(i,j) + (1.0 - alpha_12 * dt / dx) * deltaL; % セル境界(i+1/2)左側の値
urx(i + 1,j) = u(i + 1,j) - (1.0 + alpha_12*dt / dx) * deltaR; % セル境界(i+1/2)右側の値
end
end
end
function [uly, ury] = reconstruction_2nd_uds_y(i_max, j_max, u, uly, ury, ay, dt, dy)
eps = 1;
kappa = -1;
for i = 2 : i_max - 2
for j = 2 : j_max - 2
alpha_12 = ay;
deltaL = eps * (0.25 * (1 - kappa) * (u(i,j) - u(i,j - 1))...
+ 0.25 * (1 + kappa) * (u(i,j + 1) - u(i,j)) );
deltaR = eps *(- 0.25 * (1 + kappa) * (u(i,j + 1) - u(i,j))...
- 0.25 * (1 - kappa) * (u(i,j + 2) - u(i,j + 1)));
uly(i,j + 1) = u(i,j) + (1.0 - alpha_12 * dt / dy) * deltaL; % セル境界(i+1/2)左側の値
ury(i,j + 1) = u(i,j + 1) - (1.0 + alpha_12*dt / dy) * deltaR; % セル境界(i+1/2)右側の値
end
end
endおわりに
今回は2次元線形移流方程式を様々なスキームで解きました。中でもTVD法は線形解法と比較して優れた波形の保存性を有していることが分かりました。また、2次元にすることで、1次元では見えていなかった各スキームの特徴も確認することができました。実際計算してみて思いましたが、不連続波形の斜め移流問題は見る見るうちに解を破壊しますね。怖い。
移流スキームとして結局どれがベストなのかは難しいところですが、振動を避けつつも、ある程度波形は維持するという点で、個人的にはminmod limiterあたりを選択しておくのが無難かなと思いました。
さらなる精度向上にはWENO、CIPといったより高度な非線形解法が必要となりそうです。ただし、これら手法はアルゴリズムが複雑であり、計算量も増大するため、やみくもに使えばいいというわけでもない気がします。その点TVD法は比較的低コストで、他の線形スキームへの切り替えも容易なので、バランス的には悪くないのかもしれません。
参考文献
[1] 肖 鋒, “数値流体解析の基礎- Visual C++とgnuplotによる圧縮性・非圧縮性流体解析 -“, コロナ社, 2020
[2] C. Hirsch, “Numerical Computation of Internal and External Flows Volume 2: Computational Methods for Inviscid and Viscous Flows“ , John Wiley & Son Ltd , 1990/05



コメント