はじめに
過去の記事において、2次元線形移流方程式を有限体積法で解きました。今回は移流方程式との相違点に着目しながら、同様のアプロ―チで改めて拡散方程式を解きます。
拡散方程式の性質
２次元拡散方程式は拡散係数\(D\)を用いて、次のように書けます。
\frac{\partial q}{\partial t}= D\left(\frac{\partial^2 q}{\partial x^2}+\frac{\partial^2 q}{\partial y^2}\right)\tag{1}
\end{align}
2次元の微分演算子を用いると以下のような保存則の形式として書くこともできます。
\frac{\partial q}{\partial t}= D\mathrm{div} \left(\mathrm{grad} \,q\right)\tag{2}
\end{align}
一方、同様に流れの性質を表す2次元線形移流方程式は次式にて与えられました（過去記事参照）。
\frac{\partial q}{\partial t}&= -\mathrm{div} \left(\boldsymbol{a}q\right)\\
&= -\mathrm{div} \boldsymbol{f}_{adv}\tag{3}
\end{align}
式\((2)\)と式\((3)\)を比較すると、拡散方程式において流束\(\boldsymbol{f}_{diff}\)は次式で書けることが分かります。
\boldsymbol{f}_{diff}&= -D\mathrm{grad} \,q\tag{4}
\end{align}
流束とは「単位時間あたりに単位面積を通過する物理量\(q\)の総量」でした（過去記事参照）。つまり式\((4)\)は「拡散方程式において勾配\(\mathrm{grad}\, q\)が正のとき、\(q\)は負方向に移動し、勾配\(\mathrm{grad}\, q\)が負のとき、\(q\)は正方向に通過する。」ということを意味しています。坂道を転がっていくようなイメージです。
勾配\(\mathrm{grad} \,q\)が増加する場合（\(\mathrm{div} \boldsymbol{f}_{diff}>0\)）、式\((2)\)より正の湧き出しが発生し、次のタイムステップで\(q\)が増加します(\(\frac{\partial q}{\partial t}>0\))。\(\mathrm{div} \boldsymbol{f}_{diff}\)は空間二階微分を表すので、これが正であるとき\(q\)のプロファイルは下凸形状であることを意味します。つまり、\(q\)のプロファイルは下凸形状であるとき、次のタイムステップで\(q\)が増加します。反対に勾配\(\mathrm{grad} \,q\)が減少する場合（\(\mathrm{div} \boldsymbol{f}_{diff}<0\)）、\(q\)のプロファイルは上凸形状であり、次のタイムステップで減少します。
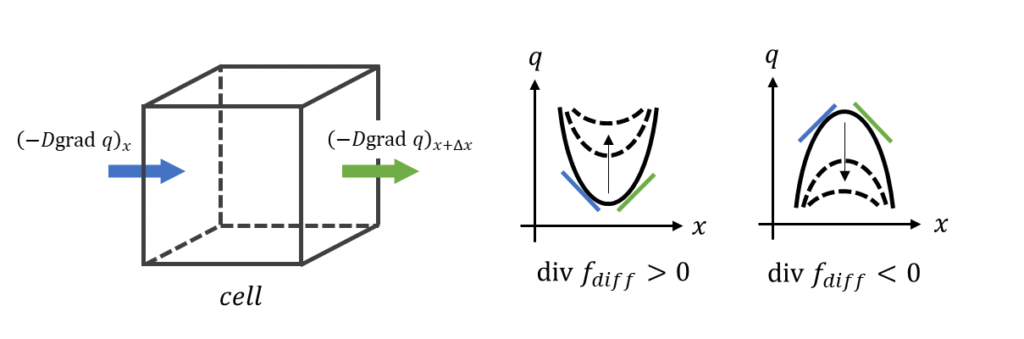
以上のように、拡散方程式は物理量のムラを時間とともに均一化する性質を有しています。
有限体積法による２次元拡散方程式の離散化
次に構造格子を想定し、拡散方程式\((2)\)を離散化します。２次元有限体積法では、離散変数がセル\(CV\)内での空間平均値として次のように与えられることに注意しましょう。
\bar{q}_{i,j}(t)=\frac{1}{\Delta V}\left(\int_{CV_{i,j}}q\left(x,y,t\right)dV\right)
\tag{5}
\end{align}
ここで、今回は２次元を考えているので、\(z\)方向は有限の厚み\(\delta\)とし、\(dV=\delta dxdy\)と置くこととします。
まずはじめに、式\((2)\)の両辺を積分し、単一セル空間、微小時間に関して平均化します。
\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}&\int_{CV_{i,j}}\left(\frac{\partial q}{\partial t}\right)dVdt=\frac{1}{\Delta V \Delta t} \int_{t}^{t+\Delta t}\int_{CV_{i,j}} D\mathrm{div} \left(\mathrm{grad}\, q\right)dVdt\tag{6}
\end{align}
上式について積分を実行します。まずは左辺から計算しましょう。
（式(6)左辺）&=\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int_{CV_{i,j}}\left(\frac{\partial q}{\partial t}\right)dVdt\\
&= \frac{1}{\Delta t}\frac{\partial }{\partial t}\int_{t}^{t+\Delta t} \frac{1}{\Delta V}\left(\int_{CV_{i,j}}qdV\right)dt
\\
&= \frac{1}{\Delta t}\frac{\partial }{\partial t}\int_{t}^{t+\Delta t}\bar{q}_{i,j}dt\\
&= \frac{1}{\Delta t}\left[\bar{q}_{i,j}(t)\right]_{t}^{t+\Delta t}\\
&= \frac{\bar{q}_{i,j}(t+\Delta t)-\bar{q}_{i,j}(t)}{\Delta t}\\
&= \frac{\bar{q}_{i,j}^{n+1}-\bar{q}_{i,j}^{n}}{\Delta t}
\tag{7}
\end{align}
次に式\((2)\)の右辺について考えます。ガウスの発散定理を用いて、発散の体積分を面積分へと変換します。
（式(2)右辺）&=\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int_{CV_{i,j}} D\mathrm{div} \left(\mathrm{grad}\, q\right)dVdt\\
&=\frac{D}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int\left(\mathrm{grad} q\right)\cdot \boldsymbol{n}dSdt\\
&=\frac{D}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\left\{\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
\left(
\begin{array}{c}
\frac{\partial q }{\partial x} \\
\frac{\partial q }{\partial y}
\end{array}
\right)_{x_{i+\frac{1}{2}}}
\cdot
\left(
\begin{array}{c}
1 \\
0
\end{array}
\right)
\delta dy
+
\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
\left(
\begin{array}{c}
\frac{\partial q }{\partial x} \\
\frac{\partial q }{\partial y}
\end{array}
\right)_{x_{i-\frac{1}{2}}}
\cdot
\left(
\begin{array}{c}
-1 \\
0
\end{array}
\right)
\delta dy
\right.\\
&\quad\quad\quad\quad\quad\quad\quad\quad\quad
+
\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}
\left.
\left(
\begin{array}{c}
\frac{\partial q }{\partial x} \\
\frac{\partial q }{\partial y}
\end{array}
\right)_{y_{j+\frac{1}{2}}}
\cdot
\left(
\begin{array}{c}
0 \\
1
\end{array}
\right)
\delta dx
+
\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}
\left(
\begin{array}{c}
\frac{\partial q }{\partial x} \\
\frac{\partial q }{\partial y}
\end{array}
\right)_{y_{j-\frac{1}{2}}}
\cdot
\left(
\begin{array}{c}
0 \\
-1
\end{array}
\right)
\delta dx
\right\}dt\\
&=\frac{D}{\Delta x \Delta y\Delta t}\int_{t}^{t+\Delta t}\left\{\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial x}\right)_{x_{i+\frac{1}{2}}}
dy
–
\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial x}\right)_{x_{i-\frac{1}{2}}}
dy
\right.\\
&\quad\quad\quad\quad\quad\quad\quad\quad\quad
+
\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}
\left.
\left(
\frac{\partial q }{\partial y}
\right)_{y_{i+\frac{1}{2}}}
dx
–
\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}
\left(
\frac{\partial q }{\partial y}
\right)_{y_{i-\frac{1}{2}}}
dx
\right\}dt
\tag{8}
\end{align}
最後の行では、\(\Delta V =\delta\Delta x \Delta y \)の関係式を用いました。
ここで例えば、右辺中括弧内１項目の\(\frac{1}{\Delta y}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial x}\right)_{x_{i+\frac{1}{2}}}
dy\)は\(x_{i+\frac{1}{2}}\)セル界面における\(\left(\frac{\partial q }{\partial x}\right)_{x_{i+\frac{1}{2}}}(y)\)の\(y\)に関する平均値を示しています。これはセル界面を単位時間に通過する物理量の総和であり、数値流束\(f_{i+\frac{1}{2},j}\)に他なりません。２～３項目も同様の記号で表すと式\((8)\)は次のように書けます。
&=\frac{D}{\Delta t}\int_{t}^{t+\Delta t}\left(\frac{f_{i+\frac{1}{2},j}
–
f_{i-\frac{1}{2},j}}{\Delta x}
+
\frac{
f_{i,j+\frac{1}{2}}
–
f_{i,j-\frac{1}{2}}}{\Delta y}
\right)dt
\tag{9}
\end{align}
ここで、\(f_{i+\frac{1}{2},j},f_{i-\frac{1}{2},j},f_{i,j+\frac{1}{2}},f_{i,j-\frac{1}{2}}\)はそれぞれ次の通りです。
f_{i+\frac{1}{2},j}=\frac{1}{\Delta y}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial x}\right)_{x_{i+\frac{1}{2}}}
dy\tag{10}\\
f_{i-\frac{1}{2},j}=\frac{1}{\Delta y}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial x}\right)_{x_{i-\frac{1}{2}}}
dy\tag{11}\\
f_{i,j+\frac{1}{2}}=\frac{1}{\Delta x}\int_{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial y}\right)_{y_{j+\frac{1}{2}}}
dx\tag{12}\\
f_{i,j-\frac{1}{2}}=\frac{1}{\Delta x}\int_{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial y}\right)_{y_{j-\frac{1}{2}}}
dx\tag{13}\\
\end{align}
次に式\((9)\)の時間積分について考えます。本来、数値流束\(f_{i+\frac{1}{2},j}\)は時間に依存するため、時間の関数として表現したうえで積分を実行すべきです。ただし、数値流束は時間方向にも離散化されているため、離散化された数値流束\(f_{i+\frac{1}{2},j}^{n}\)や\(f_{i+\frac{1}{2},j}^{n+1}\)などを用いて数値流束\(f_{i+\frac{1}{2},j}\)の時間依存性を表現する必要があります。
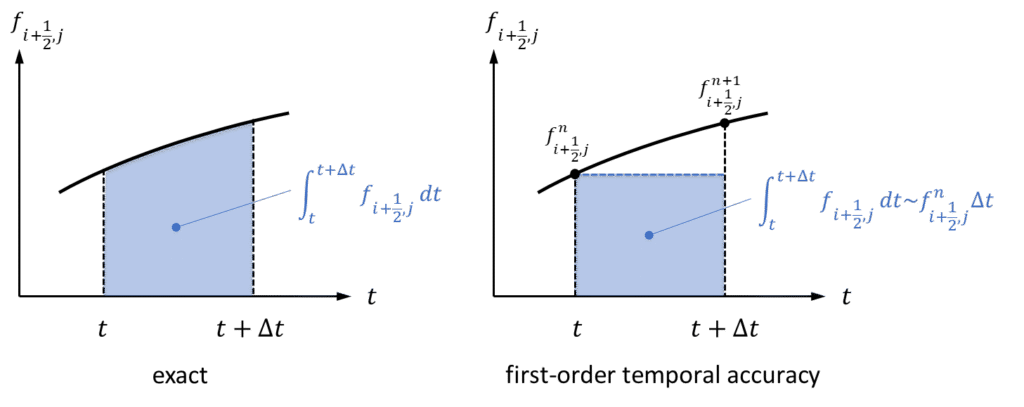
今回は時間一次精度とし、\(t \sim t + \Delta t\)の間の時間変動は考慮しない（\(f_{i+\frac{1}{2},j}=f_{i+\frac{1}{2},j}^{n}\)）ものとして、計算することとします。このとき、数値流束は定数として積分の外に出すことが出来ます。
&=\frac{D}{\Delta t}\left(\frac{f_{i+\frac{1}{2},j}^{n}
–
f_{i-\frac{1}{2},j}^{n}}{\Delta x}
+
\frac{
f_{i,j+\frac{1}{2}}^{n}
–
f_{i,j-\frac{1}{2}}^{n}}{\Delta y}
\right)\int_{t}^{t+\Delta t}dt\\
&=D\left(\frac{f_{i+\frac{1}{2},j}^{n}
–
f_{i-\frac{1}{2},j}^{n}}{\Delta x}
+
\frac{
f_{i,j+\frac{1}{2}}^{n}
–
f_{i,j-\frac{1}{2}}^{n}}{\Delta y}
\right)
\tag{14}
\end{align}
また、拡散方程式の場合、数値流束はセル界面の勾配を表すため、セル平均値\(\bar{q}_{i,j},\bar{q}_{i+1,j}\)などを用いて次のように離散化します。
f_{i+\frac{1}{2},j}=\frac{1}{\Delta y}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial x}\right)_{x_{i+\frac{1}{2}}}
dy=\frac{\bar{q}_{i+1,j}-\bar{q}_{i,j}}{\Delta x}\tag{15}\\
f_{i-\frac{1}{2},j}=\frac{1}{\Delta y}\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial x}\right)_{x_{i-\frac{1}{2}}}
dy=\frac{\bar{q}_{i,j}-\bar{q}_{i-1,j}}{\Delta x}\tag{16}\\
f_{i,j+\frac{1}{2}}=\frac{1}{\Delta x}\int_{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial y}\right)_{y_{j+\frac{1}{2}}}
dx=\frac{\bar{q}_{i,j+1}-\bar{q}_{i,j}}{\Delta y}\tag{17}\\
f_{i,j-\frac{1}{2}}=\frac{1}{\Delta x}\int_{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}
\left(\frac{\partial q }{\partial y}\right)_{y_{j-\frac{1}{2}}}
dx=\frac{\bar{q}_{i,j}-\bar{q}_{i,j-1}}{\Delta y}\tag{18}\\
\end{align}
上記、式\((15)\sim(18)\)を式\((9)\)に代入します。
&=D\left\{\frac{1}{\Delta x}\left(\frac{\bar{q}_{i+1,j}^{n}-\bar{q}_{i,j}^{n}}{\Delta x}
-\frac{\bar{q}_{i,j}^{n}-\bar{q}_{i-1,j}^{n}}{\Delta x}\right)
+\frac{1}{\Delta y}\left(\frac{\bar{q}_{i,j+1}^{n}-\bar{q}_{i,j}^{n}}{\Delta y}
-\frac{\bar{q}_{i,j}^{n}-\bar{q}_{i,j-1}^{n}}{\Delta y}\right)
\right\}\\
&=D\left\{\frac{\bar{q}_{i+1,j}^{n}-2\bar{q}_{i,j}^{n}+\bar{q}_{i-1,j}^{n}}{(\Delta x)^2}
+\frac{\bar{q}_{i,j+1}^{n}-2\bar{q}_{i,j}^{n}+\bar{q}_{i,j-1}^{n}}{(\Delta y)^2}
\right\}
\tag{19}
\end{align}
以上、式\((7),(19)\)を式\((6)\)に代入すると次式が得られます。
&\frac{\bar{q}_{i,j}^{n+1}-\bar{q}_{i,j}^{n}}{\Delta t}=D\left\{\frac{\bar{q}_{i+1,j}^{n}-2\bar{q}_{i,j}^{n}+\bar{q}_{i-1,j}^{n}}{(\Delta x)^2}
+\frac{\bar{q}_{i,j+1}^{n}-2\bar{q}_{i,j}^{n}+\bar{q}_{i,j-1}^{n}}{(\Delta y)^2}
\right\}\\
&\Leftrightarrow
\bar{q}_{i,j}^{n+1}=\bar{q}_{i,j}^{n}+D\Delta t\left\{\frac{\bar{q}_{i+1,j}^{n}-2\bar{q}_{i,j}^{n}+\bar{q}_{i-1,j}^{n}}{(\Delta x)^2}
+\frac{\bar{q}_{i,j+1}^{n}-2\bar{q}_{i,j}^{n}+\bar{q}_{i,j-1}^{n}}{(\Delta y)^2}
\right\}
\tag{20}
\end{align}
以上が有限体積法による拡散方程式の離散化式です。差分法を用いた場合と全く同じ形になりますが、離散変数がセル「平均値」となっている点が異なります。（差分法の離散変数はセル「中心値」。）
移流方程式との比較
拡散方程式の数値流束は式\((15)\sim(18)\)のように比較的シンプルに離散化できました。一方、移流方程式の離散化プロセスは、もう少し複雑でした。改めて移流方程式における数値流束の離散化プロセスを振り返り、両者の違いについて考察してみます。線形移流方程式の場合、数値流束は以下のように書けました（過去記事参照）。
f_{i+\frac{1}{2},j}=\frac{a_{x}}{\Delta y }\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}q\left(x_{i+\frac{1}{2}},y\right)dy \tag{21}\\
f_{i-\frac{1}{2},j}=\frac{a_{x}}{\Delta y }\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}q\left(x_{i-\frac{1}{2}},y\right)dy \tag{22}
\end{align}
拡散方程式の場合、界面物理量として求める値は\(\left(\frac{\partial q }{\partial x}\right)_{x_{i+\frac{1}{2}}}\)などの\(q\)の一階微分でしたが（式\((15)\sim(18)\)）、移流方程式の場合は\(q\)そのものの界面での値\(q\left(x_{i+\frac{1}{2}},y\right)\)を求めます。
この時、右辺のセル界面の物理量\(q\left(x_{i+\frac{1}{2}},y\right),q\left(x_{i-\frac{1}{2}},y\right)\)を高精度に求めるため、補間関数\(Q(x,y)\)を用いて、セル界面左右の物理量\({}^{L}q\left(x_{i+\frac{1}{2}},y\right),{}^{R}q\left(x_{i+\frac{1}{2}},y\right)\)などを求めました。さらに、これらについてリーマンソルバを用いて、風上側の界面物理量を選択することで、数値的な安定性を考慮しました。
例えば、移流方程式も補間関数やリーマンソルバなどいちいち考えず、式\((15)\sim(18)\)のようにセル界面物理量を
\frac{a_{x}}{\Delta y }\int_{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}q\left(x_{i+\frac{1}{2}},y\right)dy =a_{x}\frac{\bar{q}_{i+1,j}+\bar{q}_{i,j}}{2} \tag{23}
\end{align}
などと単純に表現し、中心差分法として定式化することも出来ます。しかしながら、中心差分法は移流方程式の性質上、数値的不安定性を招いてしまいます。また高次精度化に対するアプローチが明確ではありません。
このような理由から、移流方程式の離散化ではセル界面左右の物理量\({}^{L}q\left(x_{i+\frac{1}{2}},y\right),{}^{R}q\left(x_{i+\frac{1}{2}},y\right)\)や、リーマンソルバといった拡散方程式の離散化では存在しない概念が現れ、比較的複雑な定式化となると考えられます。
解析条件
初期条件は、次式で定義される２次元矩形波を与えることとします。
\bar{\cal{q}}_{i,j}=
\begin{cases}
1 & \text{$ \frac{n_{x}}{2}-10 <i< \frac{n_{x}}{2}+10 \quadかつ \quad \frac{n_{y}}{2}-10 <j< \frac{n_{y}}{2}+10$} \\
0.1 & \text{$others$}
\end{cases}
\tag{42}
\end{align}
ここで\(n_{x},n_{y}\)は各方向のセル数を表します。
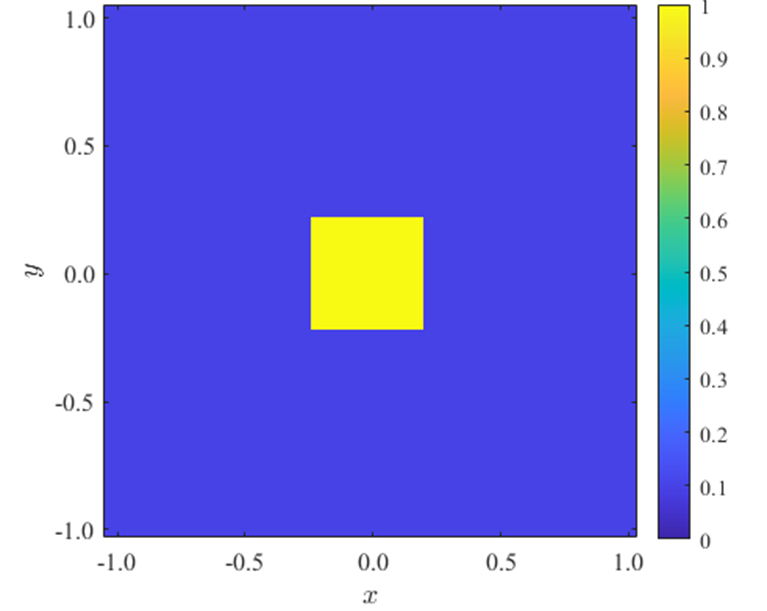
境界条件はいずれもノイマン境界条件（\(\frac{\partial q}{\partial x}=\frac{\partial q}{\partial y}=0\)）で与えます。
その他の計算パラメーターは下表にて与えることとします。
解析結果
解析結果のアニメーションを以下に示します。時間とともに矩形形状が拡散していく様子が確認できます。
MATLABコード
以下に今回使用したMATLABコードを記載します。
% 初期化
clearvars;
% パラメーター
i_max = 100; % 格子セル数
j_max = 100; % 格子セル数
XL = -1.0; % 計算領域左端の座標
XR = 1.0; % 計算領域右端の座標
YL = XL; % 計算領域左端の座標
YR = XR; % 計算領域右端の座標
tstop = 2.0; % 計算停止時刻
N_Ghost = 1; % 境界条件用のゴーストセルの数。
% 配列定義
i = 0; % セル番号； (i番目セルの左境界の番号はi、右辺境界の番号はi+1とする)
x = zeros(i_max + N_Ghost, j_max + N_Ghost); % セル境界の座標
y = zeros(i_max + N_Ghost, j_max + N_Ghost); % セル境界の座標
q = zeros(i_max + N_Ghost, j_max + N_Ghost); % セル平均値 （数値解）
n = 0; % 時間ステップ
t = 0; % 計算時間
% 拡散係数
D = 0.01;
% 格子間隔 計算領域外にゴーストセルを準備(プラス側マイナス側で１ずつ)
dx = (XR - XL) / (i_max - (2 * N_Ghost));
dy = (YR - YL) / (j_max - (2 * N_Ghost));
% 時間刻み
dt = 0.01;
% 安定条件
r = D * dt /(dx)^2;
if r > 0.5
%error('安定条件を満たしていません：r = %.4f > 0.5', r);
end
% 計算領域外(左側)の２セルも考慮した座標を振る。
x(1,:) = XL - N_Ghost * dx;
y(:,1) = YL - N_Ghost * dy;
% 計算格子，時間刻み，初期条件を設定する
[x,y,q] = initc(i_max, j_max, x, y, dx, dy, q);
% メインループ
while t <= tstop
% 時間発展
n = n + 1;
t = t + dt;
% 時間積分
for i = 1 + N_Ghost : i_max - N_Ghost % ゴーストセルを除いた範囲で計算
for j = 1 + N_Ghost : j_max - N_Ghost
q(i,j) = q(i,j) + D*dt *((q(i+1,j)-2*q(i,j)+q(i-1,j))/(dx)^2+(q(i,j+1)-2*q(i,j)+q(i,j-1))/(dy)^2);% 更新する
end
end
% 境界条件
q(1 , :) = q(1 + N_Ghost, :) ;
q(i_max + N_Ghost , :) = q(i_max, :) ;
q(: , 1) = q(:,1 + N_Ghost) ;
q(: , j_max + N_Ghost) = q(: , j_max) ;
% 出力
fprintf("n=%d, t=%f \n", n, t);
% 動画保存
if n == 1
plotconfig(x(1 : end - 1,1 : end - 1),y(1 : end - 1,1 : end - 1), q, t)
filename = ['q.mp4'];
v = VideoWriter(filename, 'MPEG-4');
v.FrameRate = 40;
open(v);
else
plotconfig(x,y, q, t)
frame = getframe(gcf);
writeVideo(v,frame);
end
end
% 動画ファイルを閉じる
close(v);
%% 以下ローカル関数
function [x,y,q] = initc(i_max, j_max, x, y, dx, dy, q)
for i = 2 : i_max + 1
for j = 1 : j_max + 1
x(i,j) = x(i - 1,j) + dx;% 格子点の座標
end
end
for i = 1 : i_max + 1
for j = 2 : j_max + 1
y(i,j) = y(i ,j - 1) + dy;% 格子点の座標
end
end
% 矩形波分布の定義
for i = i_max / 2 - 10 : i_max / 2 + 10
for j = j_max / 2 - 10 : j_max / 2 + 10
q(i,j) = 1.0;
end
end
end
function [] = plotconfig(x, y, q, t)
% レンジの決定
xmin = min(x(:,1));
xmax = max(x(:,1));
ymin = min(y(1,:));
ymax = max(y(1,:));
% imagesc の第1, 第2引数に [xmin, xmax], [ymin, ymax] を指定
imagesc([xmin, xmax], [ymin, ymax], imrotate(q, 90), [0, 1]);
colorbar;
title(['time = ', num2str(t, '%.3f')]);
% 背景を白に
fig=gcf;
fig.Color='white';
% 軸ラベルやフォント設定
xlabel('$$x$$','Interpreter','latex','FontSize',12);
ylabel('$$y$$','Interpreter','latex','FontSize',12);
set(gca, 'FontName','Times New Roman', 'FontSize',12);
% 軸のアスペクト比・表示範囲の設定
axis('equal');
axis('tight');
% Y軸のカスタム目盛りを設定
ytick_values = linspace(-1.0, 1.0, 5); % Y軸の目盛り値
ytick_labels = flip(ytick_values); % ラベルを反転
set(gca, 'YTick', ytick_values, 'YTickLabel', arrayfun(@(v) sprintf('%.1f', v), ytick_labels, 'UniformOutput', false));
% 'TickLabelFormat'を利用してX軸の桁数を指定
ax = gca;
ax.XAxis.TickLabelFormat = '%.1f'; % X軸の桁数を小数点以下2桁に設定
endおわりに
今回は2次元拡散方程式を有限体積法で解きました。基本的な内容でしたが、移流方程式の離散化と比較することで、有限体積法の理解をより深めることが出来ました。次のステップではここまでの内容を組み合わせて、NS方程式を有限体積法で解いてみたいと思います。
参考文献
[1] H.K.Versteeg、数値流体力学 [第2版]、2011/5/31
コメント