はじめに
今回はコロケート格子を用いた2次元キャビティフローを計算する方法についてまとめていきます。書いてるうちに長くなってしまったので、実際の実装は次回の記事として、この記事ではコロケート格子でナビエ・ストークス方程式を離散化する部分について記載したいと思います。なお今回実装を行うスキームは下表の内容です。第一弾ということで、高度なことは考えず基本的な内容で実装していく方針とします。
| 項目 | 内容 |
|---|---|
| 時間離散化手法 | 前進オイラー法 |
| 空間離散化手法 | 有限差分法 |
| 拡散項の離散化 | 2次精度中心差分法 |
| 移流項の離散化 | 1次精度風上差分法 |
| 圧力項の離散化 | 2次精度中心差分法 |
| 圧力-速度連成解法 | SMAC法 |
| 圧力ポアソン方程式の求解 | SOR法 |
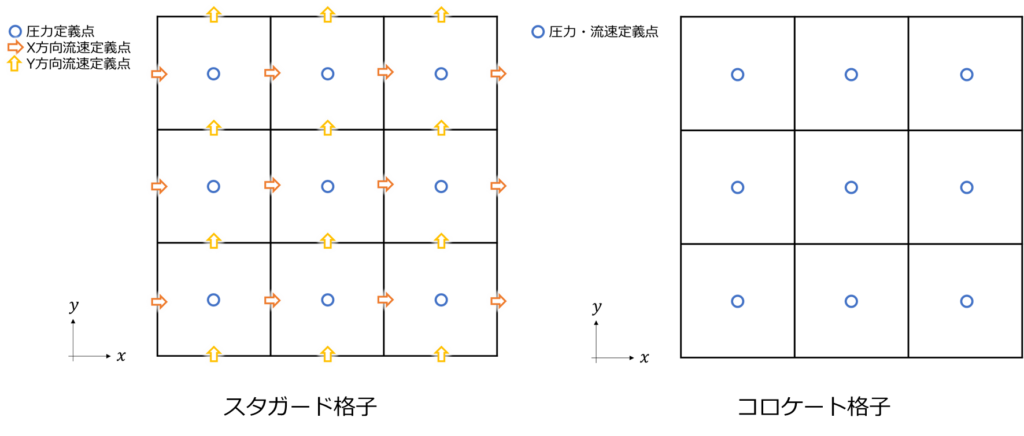
スタガード格子とコロケート格子
まずスタガード格子とコロケート格子についておさらいしておきます。
スタガード格子は圧力をセル中心に、流速をセル界面に位相をずらして配置する格子でした。圧力の離散化によって生じるいわゆる「チェッカーボード不安定」を完全に打ち消すことが出来ます。またこの配置は「セル中心の圧力によってセル界面の流速が駆動する」ことを意味し、ナビエストークス方程式の構造を自然に再現しているとも言えます。一方で圧力と流速と互い違いに配置するという性質上、非構造格子への適用は困難です。同様の理由でプログラミングも若干複雑になります。
コロケート格子は圧力・流速ともにセル中心に配置する格子です。「チェッカーボード不安定性」はRhie-Chow補間により回避されます。これによりスタガート格子と比べて、若干精度は落ちますが、プログラミングがシンプルになり、非構造格子への拡張が容易となります。これらのメリットから多くの商用ソルバではコロケート格子が用いられています。
数値流体力学の教科書などで実装が紹介されるのはスタガード格子であることが多いようです。しかし実際実装してみると、境界条件の与え方などやや複雑で個人的には少し苦手です。この為今回はコロケート格子を用いた実装を行おうと思います。
| スタガード格子 | コロケート格子 | |
|---|---|---|
| メリット | ・チェッカーボード不安定性が現れない。 | ・プログラミングが比較的容易。 ・非構造格子への対応が可能。 |
| デメリット | ・プログラミングが比較的複雑 ・非構造格子への対応が困難 | ・チェッカーボード不安定性回避のためRhie-Chow 補間が必要。 ・若干精度が悪い。 |
基礎方程式
基礎方程式は、下記の2次元非圧縮ナビエ・ストークス方程式
&\frac{\partial }{\partial t}
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
+
\left[
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
\right]
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
=-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
p
+
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial x^2} + \frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial x^2} +\frac{\partial ^2 }{\partial y^2}
\end{array}
\right)
\left(
\begin{array}{c}
u \\
v
\end{array}
\right) \\\\
&→
\frac{\partial }{\partial t}
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
=
-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
p
+
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial x^2} + \frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial x^2} +\frac{\partial ^2 }{\partial y^2}
\end{array}
\right)
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
–
\left[
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
\right]
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)\tag{1}
\end{align}
及び連続の方程式
\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\tag{2}
\end{align}
の3つです。これらの式をSMAC法で解いていきます。
SMAC法について
ここでSMAC法についておさらいしておきます。詳しくは以下の記事にて紹介してるので興味のある方はご覧ください。
SMAC法のアルゴリズムは以下のとおりでした。

上記フローより、まずは中間速度\(u^*,v^*\)を求める必要があります。中間速度の式を再度書き下すと以下のようになります。
&\frac{1}{\Delta t}
\left [
\left(
\begin{array}{c}
u^{*} \\
v^{*}\\
\end{array}
\right)
–
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\right]
=
-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
p^{n}
+
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial x^2} + \frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial x^2} +\frac{\partial ^2 }{\partial y^2}\\
\end{array}
\right)
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
–
\left[
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
\right]
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\\\\
&→
\left(
\begin{array}{c}
u^{*} \\
v^{*}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
+
\Delta t
\left\{
-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
p^{n}
+
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial x^2} + \frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial x^2} +\frac{\partial ^2 }{\partial y^2}\\
\end{array}
\right)
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
–
\left[
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
\right]
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\right\}
\tag{3}
\end{align}
この式はすでに時間に関して前進オイラー法で離散化されています。中間速度\(u^*,v^*\)を求めるには、右辺の圧力項(第2項)、拡散項(第3項)、移流項(第4項)を計算する必要があります。そこで次からコロケート格子を用いてこれらの空間離散化を考えていきます。
拡散項の離散化
まずは最も簡単な拡散項(式\((3)\)の右辺第3項)
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial x^2} + \frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial x^2} +\frac{\partial ^2 }{\partial y^2}\\
\end{array}
\right)
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\tag{4}
\end{align}
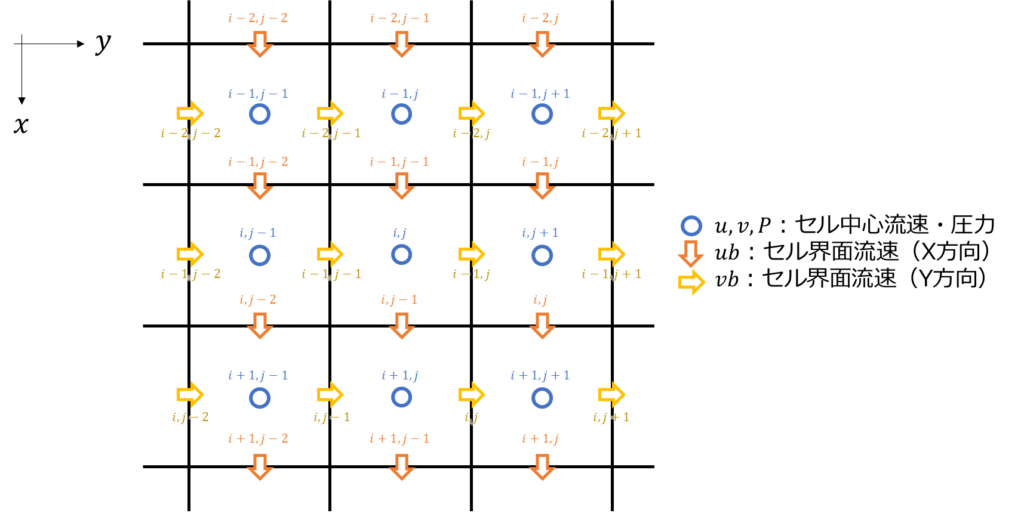
の空間離散化を行います。コロケート格子は以下のような配置・座標系で考えることとします。

ここで\(x\)方向を下向きにとった座標系となっていますが、これは配列の行を\(x\)方向、列を\(y\)方向と紐づけて考えるためで、実装上の都合です。
また拡散項には空間に関する二階微分が含まれています。拡散現象は方向性がないので、これについては2次精度中心差分法で離散化する方針とします。実際に計算すると以下のように書けます。
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial x^2} + \frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial x^2} +\frac{\partial ^2 }{\partial y^2}\\
\end{array}
\right)
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
=
ν
\left(
\begin{array}{c}
\frac{u^{n}_{i+1,j}-2u^{n}_{i,j}+u^{n}_{i-1,j}}{\Delta x^2} + \frac{u^{n}_{i,j+1}-2u^{n}_{i,j}+u^{n}_{i,j-1} }{\Delta y^2}\\
\frac{v^{n}_{i+1,j}-2v^{n}_{i,j}+v^{n}_{i-1,j} }{\Delta x^2} +\frac{v^{n}_{i,j+1}-2v^{n}_{i,j}+v^{n}_{i,j-1} }{\Delta y^2}\\
\end{array}
\right)
\tag{5}
\end{align}
以上が拡散項の離散化になります。
移流項の離散化
次に移流項(式\((3)\)の右辺第4項)
–
\left[
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
\right]
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
=
-\left(
\begin{array}{c}
u^{n}\frac{\partial u^{n}}{\partial x}+v^{n}\frac{\partial u^{n}}{\partial y}\\
u^{n}\frac{\partial v^{n}}{\partial x}+v^{n}\frac{\partial v^{n}}{\partial y}\\
\end{array}
\right)
\tag{6}
\end{align}
の空間離散化を進めます。離散化は拡散項と同様の格子(図2)で行います。また一階微分は安定性確保のため、後退差分近似で計算します。
-\left(
\begin{array}{c}
u^{n}\frac{\partial u^{n}}{\partial x}+v^{n}\frac{\partial u^{n}}{\partial y}\\
u^{n}\frac{\partial v^{n}}{\partial x}+v^{n}\frac{\partial v^{n}}{\partial y}\\
\end{array}
\right)
=
-\left(
\begin{array}{c}
u^{n}_{i,j}\frac{u^{n}_{i+1,j}-u^{n}_{i-1,j}}{2\Delta x}
+\left| u^{n}_{i,j}\right|\frac{2u^{n}_{i,j}-u^{n}_{i-1,j}-u^{n}_{i+1,j}}{2\Delta x}
+v^{n}_{i,j}\frac{u^{n}_{i,j+1}-u^{n}_{i,j-1}}{2\Delta y}
+\left| v^{n}_{i,j}\right|\frac{2u^{n}_{i,j}-u^{n}_{i,j-1}-u^{n}_{i,j+1}}{2\Delta y}\\
u^{n}_{i,j}\frac{v^{n}_{i+1,j}-v^{n}_{i-1,j}}{2\Delta x}
+\left| u^{n}_{i,j}\right|\frac{2v^{n}_{i,j}-v^{n}_{i-1,j}-v^{n}_{i+1,j}}{2\Delta x}
+v^{n}_{i,j}\frac{v^{n}_{i,j+1}-v^{n}_{i,j-1}}{2\Delta y}
+\left| v^{n}_{i,j}\right|\frac{2v^{n}_{i,j}-v^{n}_{i,j-1}-v^{n}_{i,j+1}}{2\Delta y}\\
\end{array}
\right)
\tag{7}
\end{align}
右辺の絶対値記号は速度の符号に応じて常に後退差分になるように調整するためのものです。以上が移流項の離散化になります。
圧力項の離散化
次に圧力項(式\((3)\)の右辺第2項)
-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
p^{n}
\tag{8}
\end{align}
の離散化を行います。圧力項の離散化はコロケート格子における重要なポイントの一つです。まず普通にコロケート格子(図3)での離散化を考えてみましょう。圧力勾配による流速変化には方向性はないので、一回微分は中心差分で離散化すると以下のようになります。
-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
p^{n}
=
-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{p^{n}_{i+1,j}-p^{n}_{i-1,j} }{2\Delta x} \\
\frac{p^{n}_{i,j+1}-p^{n}_{i,j-1} }{2\Delta y}\\
\end{array}
\right)
\tag{9}
\end{align}
上記は一見正しく離散化できているように見えます。しかし圧力のセル間隔が一つ跳びなってしまっていることが分かります。この為、例えば流速が全域で0で静止しているとき、仮に偶数番目のセルの圧力がある一定値、奇数番目のセルが別の一定値というように、圧力場が振動的になっていても、それが検知できず、まったく流れが生じないこととなります。(いわゆる「チェッカーボード不安定性」が生じてしまう。)
これを解決するのが次に記載する「Rhie-Chow補間」です。
Rhie-Chow補間
上記より圧力項を単純に離散化しようとすると、チェッカーボード不安定性が生じてしまうことが分かりました。そこで一度圧力項の離散化は置いておいて、今一度SMAC法のアルゴリズムに立ち返ってみます。
図2より中間速度を求めた後は、連続の式の誤差\(D^{*}_{i,j}\)を計算することとなります。\(D^{*}_{i,j}\)は\((i,j)\)番目のセルにおける発散(流体の湧き出し・吸い込みの具合)を示すので、コロケート格子では、以下のようにセル界面の中間速度\(ub^{*},vb^{*}\)を用いて表現することとなります。
D^{*}_{i,j}
=
\frac{ ub^{*}_{i,j-1}-ub^{*}_{i-1,j-1}}{\Delta x}
+
\frac{ vb^{*}_{i-1,j}-vb^{*}_{i-1,j-1}}{\Delta y}
\tag{10}
\end{align}
ここでセル界面での中間速度\(ub^*,vb^*\)は単純に考えるならば式\((3)\)のセル中心の中間速度\(u^*,v^*\)用いた補間により以下のように書けます。
\left(
\begin{array}{c}
ub^{*}_{i,j}\\
vb^{*}_{i,j}\\
\end{array}
\right)
=
\frac{1}{2}
\left(
\begin{array}{c}
u^{*}_{i,j+1}+u^{*}_{i+1,j+1}\\
v^{*}_{i+1,j}+v^{*}_{i+1,j+1}\\
\end{array}
\right)
\tag{11}
\end{align}
しかし、前節でセル中心の中間速度\(u^{*},v^{*}\)を求めるために、式\((3)\)の圧力を単純に離散化しようとするとチェッカーボード不安定性が生じてしまう問題がありました。そこで以下のように考えます。
まず式\((3)\)の中で問題なく離散化できた拡散項・移流項のみ考慮したセル中心の中間速度\(u^{**},v^{**}\)を考えます。
&\left(
\begin{array}{c}
u^{**} \\
v^{**}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
+
\Delta t
\left\{
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial x^2} + \frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial x^2} +\frac{\partial ^2 }{\partial y^2}\\
\end{array}
\right)
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
–
\left[
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
\right]
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\right\}
\\\\
&→
\left(
\begin{array}{c}
u^{**} _{i,j}\\
v^{**}_{i,j}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{n}_{i,j} \\
v^{n}_{i,j}\\
\end{array}
\right)
+
\Delta t
\left\{
ν
\left(
\begin{array}{c}
\frac{u^{n}_{i+1,j}-2u^{n}_{i,j}+u^{n}_{i-1,j}}{\Delta x^2} + \frac{u^{n}_{i,j+1}-2u^{n}_{i,j}+u^{n}_{i,j-1} }{\Delta y^2}\\
\frac{v^{n}_{i+1,j}-2v^{n}_{i,j}+v^{n}_{i-1,j} }{\Delta x^2} +\frac{v^{n}_{i,j+1}-2v^{n}_{i,j}+v^{n}_{i,j-1} }{\Delta y^2}\\
\end{array}
\right)
-\left(
\begin{array}{c}
u^{n}_{i,j}\frac{u^{n}_{i+1,j}-u^{n}_{i-1,j}}{2\Delta x}
+\left| u^{n}_{i,j}\right|\frac{2u^{n}_{i,j}-u^{n}_{i-1,j}-u^{n}_{i+1,j}}{2\Delta x}
+v^{n}_{i,j}\frac{u^{n}_{i,j+1}-u^{n}_{i,j-1}}{2\Delta y}
+\left| v^{n}_{i,j}\right|\frac{2u^{n}_{i,j}-u^{n}_{i,j-1}-u^{n}_{i,j+1}}{2\Delta y}\\
u^{n}_{i,j}\frac{v^{n}_{i+1,j}-v^{n}_{i-1,j}}{2\Delta x}
+\left| u^{n}_{i,j}\right|\frac{2v^{n}_{i,j}-v^{n}_{i-1,j}-v^{n}_{i+1,j}}{2\Delta x}
+v^{n}_{i,j}\frac{v^{n}_{i,j+1}-v^{n}_{i,j-1}}{2\Delta y}
+\left| v^{n}_{i,j}\right|\frac{2v^{n}_{i,j}-v^{n}_{i,j-1}-v^{n}_{i,j+1}}{2\Delta y}\\
\end{array}
\right)
\right\}
\tag{12}
\end{align}
上記は少し長いので、拡散項を\(Diff\)、移流項を\(Adv\)と省略して以下のように表記します。
\left(
\begin{array}{c}
u^{**} _{i,j}\\
v^{**}_{i,j}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{n}_{i,j} \\
v^{n}_{i,j}\\
\end{array}
\right)
+
\Delta t
\left(
Diff+Adv
\right)
\tag{13}
\end{align}
そのうえで\(u^{**},v^{**}\)を用いてセル界面での中間速度\(ub^{*},vb^{*}\)を以下のように与えます。
\left(
\begin{array}{c}
ub^{*}_{i,j}\\
vb^{*}_{i,j}\\
\end{array}
\right)
=
\frac{1}{2}
\left(
\begin{array}{c}
u^{**}_{i,j+1}+u^{**}_{i+1,j+1}\\
v^{**}_{i+1,j}+v^{**}_{i+1,j+1}\\
\end{array}
\right)
–
\frac{\Delta t}{\rho}
\left(
\begin{array}{c}
\frac{p_{i+1,j+1}-p_{i,j+1}}{\Delta x}\\
\frac{p_{i+1,j+1}-p_{i+1,j}}{\Delta y}\\
\end{array}
\right)
\tag{14}
\end{align}
上記は式\((11)\)とは異なり、第二項に圧力項を含んでいます。このように式\((3)\)で最初から圧力項まで含めた離散化を行うのではなく、セル界面流速の補間の段階で圧力を考慮することで圧力勾配の離散化が一つとびになることを防ぐことが出来ます。これによりチェッカーボード不安定性も解消されます。このような操作をRhie-Chow補間といいます。
以上より、圧力項の離散化と\(D^*\)の計算ができるようになりました。次では圧力補正量の計算方法について述べます。
圧力の更新
SMAC法では圧力の補正量\(\delta p\)は以下の圧力のポアソン方程式を解くことで計算できました。
\left(
\frac{\partial ^2 }{\partial x^2}+\frac{\partial^2 }{\partial y^2}
\right)
\delta p
=
\frac{ρD^{*}}{\Delta t}
\tag{15}
\end{align}
次はこれを離散化していきます。これまでと同様に離散化には図3のコロケート格子を用いることとします。また圧力の二階微分は中心差分法で離散化します。
\left(
\frac{\delta p_{i+1,j}-2\delta p_{i,j}+\delta p_{i-1,j} }{\Delta x^2}+\frac{\delta p_{i,j+1}-2\delta p_{i,j}+\delta p_{i,j-1}}{\Delta y^2}
\right)
=
\frac{ρD^{*}_{i,j}}{\Delta t}
\tag{16}
\end{align}
左辺に\(\delta p_{i,j}\)だけ残せば、
&-2\left(
\frac{1}{\Delta x^2}+\frac{1}{\Delta y^2}
\right)\delta p_{i,j}
=
\frac{ρD^{*}_{i,j}}{\Delta t}
-\frac{\delta p_{i+1,j}}{\Delta x^2}
-\frac{\delta p_{i-1,j}}{\Delta x^2}
-\frac{\delta p_{i,j+1}}{\Delta y^2}
-\frac{\delta p_{i,j-1}}{\Delta y^2}
\\\\
&→
\delta p_{i,j}
=
\frac{1}{2\left(
\frac{1}{\Delta x^2}+\frac{1}{\Delta y^2}
\right)}
\left(
\frac{\delta p_{i+1,j}}{\Delta x^2}
+\frac{\delta p_{i-1,j}}{\Delta x^2}
+\frac{\delta p_{i,j+1}}{\Delta y^2}
+\frac{\delta p_{i,j-1}}{\Delta y^2}
-\frac{ρD^{*}_{i,j}}{\Delta t}
\right)
\tag{17}
\end{align}
後は適当な初期値・境界条件の下、\(\delta p\)に関する連立一次方程式を解けばよいです。連立一次方程式の解法としては、ここでは最も単純な手法の一つであるSOR法を用いることとします。式\((17)\)をSOR法のアルゴリズムの当てはめると以下のような手順となります。
まず、以下の式で圧力の修正量を求めます。
\delta p_{i,j}^{new}
=
\frac{1}{2\left(
\frac{1}{\Delta x^2}+\frac{1}{\Delta y^2}
\right)}
\left(
\frac{\delta p_{i+1,j}}{\Delta x^2}
+\frac{\delta p_{i-1,j}}{\Delta x^2}
+\frac{\delta p_{i,j+1}}{\Delta y^2}
+\frac{\delta p_{i,j-1}}{\Delta y^2}
-\frac{ρD^{*}_{i,j}}{\Delta t}
\right)
\tag{18}
\end{align}
次に上式の\(\delta p^{new}\)を用いて、以下の式に基づき\(\delta p\)を更新します。
\delta p_{i,j}
:=\delta p_{i,j}+\alpha
\left(
\delta p_{i,j}^{new}
-\delta p_{i,j}
\right)
\tag{19}
\end{align}
\(:=\)は右辺の値を左辺に代入することを意味します。また\(\alpha\)は緩和係数と呼ばれ、収束を加速させるための係数であり、多くの場合は\(\alpha \sim 1.7\)程度で用いられます。上記、式\((18)、(19)\)を収束するまで交互に計算することで\(\delta p_{i,j}\)を求めることが出来ます。
最終的な圧力は上記反復で得られた補正圧力を用いて以下の式で計算できます。
p_{i,j}^{n+1}
=p_{i,j}^{n}+\delta p_{i,j}
\tag{20}
\end{align}
流速の更新
最後に圧力に基づき流速を更新します。式\((12)\)の\(u_{i,j}^{**},v_{i,j}^{**}\)は拡散項と移流項を考慮したセル中心の流速でした。式\((3)\)にこれを代入すると以下のようになります。
&\left(
\begin{array}{c}
u^{*} \\
v^{*}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
+
\Delta t
\left\{
-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
p^{n}
+
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial x^2} + \frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial x^2} +\frac{\partial ^2 }{\partial y^2}\\
\end{array}
\right)
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
–
\left[
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
\right]
\left(
\begin{array}{c}
u^{n} \\
v^{n}\\
\end{array}
\right)
\right\}
\\\\
&→
\left(
\begin{array}{c}
u^{*} \\
v^{*}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{**} \\
v^{**}\\
\end{array}
\right)
-\frac{\Delta t}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
p^{n}
\tag{21}
\end{align}
この式をSMAC法における流速の更新式
&\frac{1}{\Delta t}
\left [
\left(
\begin{array}{c}
u^{n+1} \\
v^{n+1}\\
\end{array}
\right)
–
\left(
\begin{array}{c}
u^{*}\\
v^{*}\\
\end{array}
\right)
\right]
=
-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
\left(p^{n+1}-p^{n}\right)
\\\\
&→
\left(
\begin{array}{c}
u^{n+1} \\
v^{n+1}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{*}\\
v^{*}\\
\end{array}
\right)
-\frac{\Delta t}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
\left(p^{n+1}-p^{n}\right)
\tag{22}
\end{align}
に代入すると、
&\left(
\begin{array}{c}
u^{n+1} \\
v^{n+1}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{**} \\
v^{**}\\
\end{array}
\right)
-\frac{\Delta t}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}\\
\end{array}
\right)
p^{n+1}
\tag{23}
\end{align}
さらに中心差分法で離散化すると以下のようになります。
\left(
\begin{array}{c}
u^{n+1}_{i,j} \\
v^{n+1}_{i,j}\\
\end{array}
\right)
=
\left(
\begin{array}{c}
u^{**}_{i,j}\\
v^{**}_{i,j}\\
\end{array}
\right)
-\frac{\Delta t}{ρ}
\left(
\begin{array}{c}
\frac{p^{n+1}_{i+1,j}-p^{n+1}_{i-1,j}}{2\Delta x} \\
\frac{p^{n+1}_{i,j+1}-p^{n+1}_{i,j-1} }{2\Delta y}\\
\end{array}
\right)
\tag{24}
\end{align}
上記が圧力から流速を更新する式です。
ただ、この式を見ると圧力のセル間隔が一つ飛ばしになってしまっています。これではやはりチェッカーボード不安定性が生じてしまう気が…。式\((14)\)で一度、Rhie-Chow補間の上で、圧力の補正量を求めに行っているから、この段階でセルが一つ飛ばしになっていても問題ないのでしょうか…。正直、この辺を腹落ちさせる理解は私自身まだ得られていないです。(詳しい方教えてくださいm(__)m)
おわりに
今回はSMAC法をコロケート格子に適用する方法について記載しました。コロケート格子は補間処理が意外と厄介ですが、格子周りのプログラミングがシンプルになる点で、勉強する意義は大きいと思います。次回は実装とその検証を進めたいと思います。
参考文献
1) 牛島 省, コロケー ト格子配置を用いたMAC系解法の計算スキームに関する考察, 土木学会論文集, 2002年,2002巻719号p.11-19
2) 春日 悠, 「SMAC法」, penguinitis, 2021年10月16日, http://penguinitis.g1.xrea.com/study/note/smac.pdf
3) 肖 鋒, 数値流体解析の基礎- Visual C++とgnuplotによる圧縮性・非圧縮性流体解析 -, コロナ社, 2020


