はじめに
移流方程式は流れの特徴を表現する方程式の一つです。その解析解の振る舞いはシンプルですが数値的に正確に解くのは難しく、様々な解法が提案されています。本記事から何度かに分けて移流方程式の特徴や解法ついてまとめていきます。最初はベーシックな内容となると思いますが、最終的には実用的な移流解法までたどり着くことを目指したいと思います。
1次元移流方程式
一次元移流方程式は次式のように与えられます。
\frac{\partial q}{\partial t}+c\frac{\partial q}{\partial x}= 0\tag{1}
\end{align}
ここで\(q\)は求めるべき物理量で具体的には温度や濃度、流速などが当てはまります。定数\(c\)は物理量\(q\)の輸送速度です。ナビエ・ストークス方程式では\(c\)も変数となりますが、話を簡単にするため、まずは定数として扱います。
式\((1)\)の解析解は任意の関数\(f\)を用いて以下のように書けます。
q = f(x-ct)\tag{2}
\end{align}
関数\(f\)が解となっているのは少し不思議な感じがしますが、これが解であることは式\((2)\)を式\((1)\)に代入してみるとすぐに分かります。\(f\)はどんな形でも構いません。ただし変数が\(x-ct\)となっているので、時間とともに速さ\(c\)で初期形状を保ったまま移動していく関数となります。
例えば\(f\)が\(x\)の関数として以下のように与えられたとします。
\begin{equation}
f(x)=
\begin{cases}
1 & \text{$x \leq 1$のとき} \\
0 & \text{$x>1$のとき}
\end{cases}
\tag{3}
\end{equation}
このとき移流方程式の解としては、これが速さ\(c\)で移動するので、以下のように書けます。
\begin{equation}
q=f(x-ct)=
\begin{cases}
1 & \text{$x\leq 1+ct$のとき} \\
0 & \text{$x> 1+ct$のとき}
\end{cases}
\tag{4}
\end{equation}
\(c=1\)としてアニメーションを作成すると以下の通りです。
このように移流方程式の解は初期形状を保ったまま、速さ\(c\)で移動していくという特徴を持っています。
1次精度風上差分法
次は式\((1)\)を数値的に解くことを考えます。時間を1次精度オイラー陽解法、空間を1次精度風上差分法で離散化すると以下のように書けます。
&\frac{q^{n+1}_{j}-q^{n}_{j}}{\Delta t}+c\frac{q_{j}^{n}-q_{j-1}^{n}}{\Delta x}= 0\\
&\Leftrightarrow
q^{n+1}_{j}= q^{n}_{j}-\frac{c\Delta t }{\Delta x}\left( q_{j}^{n}-q_{j-1}^{n}\right)\tag{5}\\
\end{align}
上式より\(q\)の初期値が同じならば\(q^{n+1}_{j}\)は右辺第二項の係数\(\frac{c\Delta t }{\Delta x}\)によって決まることが分かります。\(\Delta t、\Delta x\)がどんな値を取ろうが\(\frac{c\Delta t }{\Delta x}\)さえ一致すれば同一の解となるわけです。この係数はレイノルズ数等と同様の流体の無次元数の一つで、「クーラン数\(\nu\)」と呼ばれています。
\(c\Delta t \)は物理量\(q\)が1タイムステップあたりに進む距離なので、クーラン数は「1タイムステップあたりに物理量\(q\)が進む要素数」を表した数ともいえます。
クーラン数を用いると式\((5)\)は以下のように書けます。
q^{n+1}_{j}= q^{n}_{j}-\nu\left( q_{j}^{n}-q_{j-1}^{n}\right)\tag{6}\\
\end{align}
実際に式\((6)\)を用いて数値解を求めてみます。初期条件は式\((4)\)と同様に与え、下記3パターンのパラメーターで計算します。

結果のアニメーションを以下に示します。
\(1次精度風上差分法による計算結果。上:\nu=0.5/中:\nu=1.0/下:\nu=2.0\)
アニメーションから3パターン全て異なる結果を示していることが分かります。具体的には以下の通りです。
- case1(\(\nu = 0.5\)):数値解は次第に鈍ってしまう。
- case2(\(\nu = 1\)):数値解は解析解と全く同じ形状を得ることができている。
- case3(\(\nu = 2\)):数値解は振動してしまう。
正確に解けているのはcase2だけで、その他2つの精度はよくありません。特にcase3に関しては振動による不安定な解が生じてしまっています。どうしてこのような現象が起きるのでしょうか?これを理解するために、式\((6)\)を以下のように変形します。
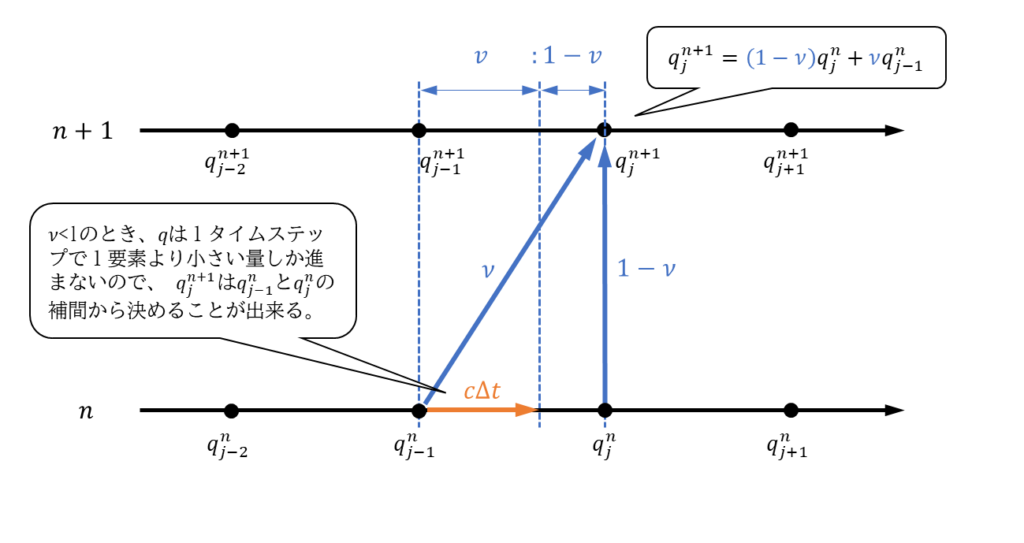
q^{n+1}_{j}= \left(1-\nu\right)q^{n}_{j}+\nu q_{j-1}^{n}\tag{7}\\
\end{align}
この式は「\(q^{n+1}_{j}\)をクーラン数を比とした\(q^{n}_{j-1}\)、\(q^{n}_{j}\)の和から決める」ことを意味しています。これはcase1においては適切な考え方と言ってよいでしょう。なぜなら、\(\nu <1\)のとき、\(q\)は1タイムステップで1要素より小さい量しか進まないので、\(q^{n+1}_{j}\)は\(q^{n}_{j-1}\)と\(q^{n}_{j}\)の補間から決めることが出来るからです。
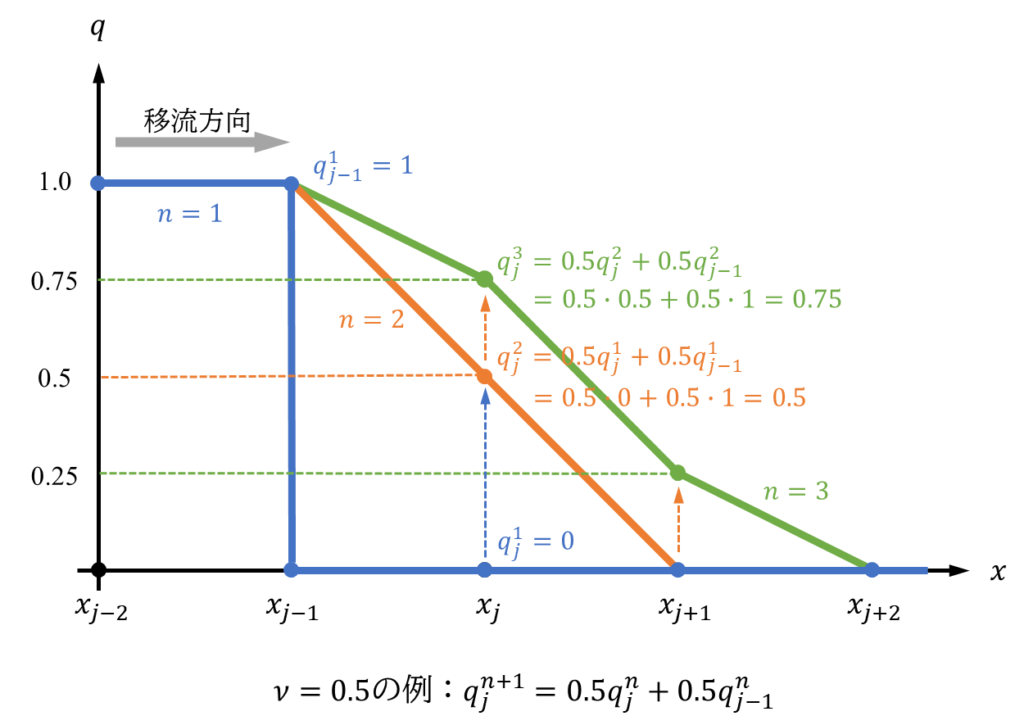
しかしながら、「\(q^{n+1}_{j}\)をクーラン数を比とした\(q_{^{n}_{j-1}}\)、\(q_{^{n}_{j}}\)の和から決める」という特性上、下図のようにちょうど\(q\)の値が1→0へ変化する位置で解が鈍る拡散現象が生じてしまいます。
一方、case2のように\(\nu = 1\)の場合、式\((7)\)は\(q^{n+1}_{j}= q_{j-1}^{n}\)となります。これはタイムステップが一つ進むとちょうど格子一つ分だけ、\(q\)の値が移動することを示しています。まさに解析解そのものの挙動です。
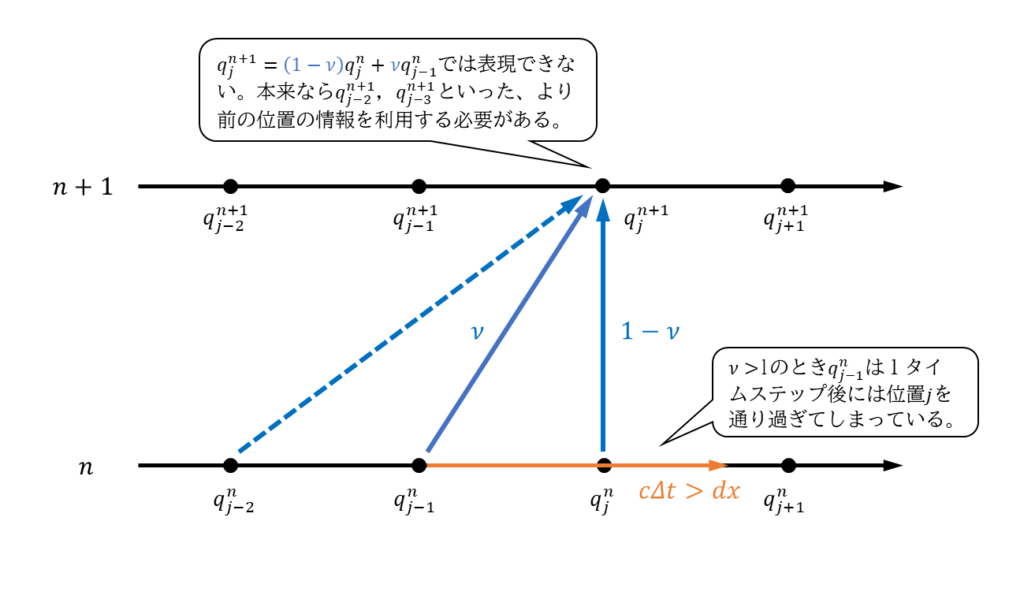
ではcase3のように\(\nu >1\)の場合はどうでしょうか?これは式\((7)\)の「\(q^{n+1}_{j}\)をクーラン数を比とした\(q^{n}_{j-1}\)、\(q^{n}_{j}\)の和から決める」という風上差分法の考え方にはそぐわない状態です。なぜなら下図のように\(q^{n}_{j-1}\)は1タイムステップ後には、位置\(j\)を通り過ぎてしまっているからです。
言い換えると\(\nu >1\)の状況では\(q_{j}^{n+1}\)は\(q^{n}_{j-1}\)より、より上流から来ているはずです。この為、\(q^{n}_{j-1}\)と\(q^{n}_{j}\)の線形和で\(q_{j}^{n+1}\)を表現できるはずもありません。
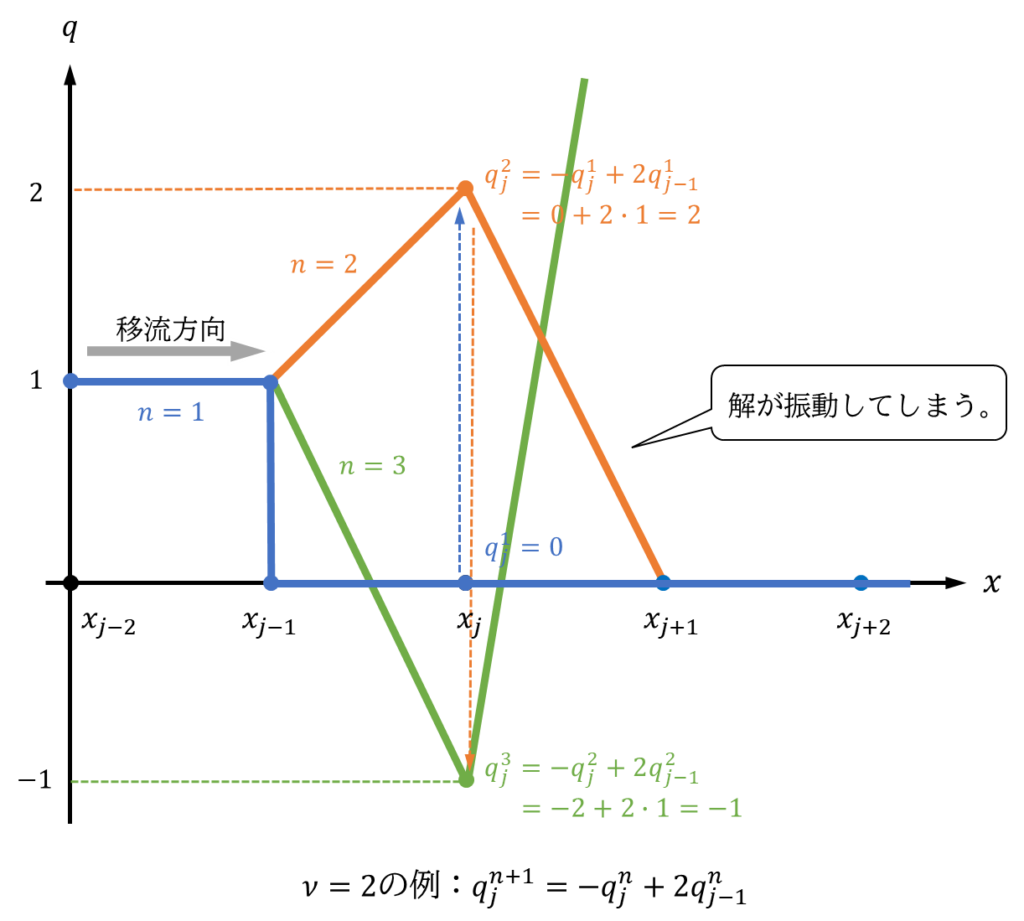
数式的にみると\(\nu >1\)のとき、式\((7)\)の右辺第一項目は負になってしまいます。係数が負になってしまうということは、物理量\(q\)が隣接点の値によって減少(ひいては振動)させることを意味しています。これにより下図のように\(q^{n+1}_{j}\)を本来は取りえない負の値にしてしまったり、1より(元の波の高さより)大きくしてしまったりと不安定な挙動を引き起こします。(実際には、係数が負で解が振動的でも、振動が増幅せず、安定な解を得られるスキームもあります。このような解の安定性の議論は本来は「フォンノイマンの安定性解析」で議論されます。)
以上をまとめると1次精度風上差分法では以下のことが言えます。
- クーラン数を1にすると解析解と同等の解が得られる。(ただし実際の問題では移流速度、メッシュ分解能は空間分布を持つので、すべての要素でクーラン数を1にするのは難しい。)
- クーラン数を1より小さくすることで、拡散してしまうが安定な解が得られる。
- クーラン数を1より大きくすることで、振動が生じ、不安定な解となってしまう。
2次精度中心差分法
次は中心差分法による離散化を考えてみます。2次精度中心差分法を用いると式\((1)\)は以下のように離散化できます。
\frac{q^{n+1}_{j}-q^{n}_{j}}{\Delta t}&+c\frac{q_{j + 1}^{n}-q_{j – 1}^{n}}{2\Delta x}= 0\\
\Leftrightarrow
q^{n+1}_{j}&= q^{n}_{j}-\frac{c\Delta t }{2\Delta x}\left( q_{j+1}^{n}-q_{j-1}^{n}\right)\\
\quad\quad\quad &= q^{n}_{j}-\frac{\nu}{2}\left( q_{j+1}^{n}-q_{j-1}^{n}\right)\tag{8}
\end{align}
上記について風上差分法の時と同様の3パターンのクーラン数で数値解を計算します。以下に結果のアニメーションを示します。
\(2次精度中心差分法による計算結果。上:\nu=0.5/中:\nu=1.0/下:\nu=2.0\)
今回はクーラン数によらず、3パターンとも見事?に振動による非物理的な挙動を示しています。これを理解するため、式\((8)\)を式\((7)\)と同様に以下のように書き換えます。
q^{n+1}_{j}= q^{n}_{j}-\frac{\nu}{2}q_{j+1}^{n}+\frac{\nu}{2}q_{j-1}^{n}\tag{9}
\end{align}
上式で右辺第二項の係数は負、第三項の係数は正になっています。風上差分法で見たように右辺の係数が負であることは、不安定な挙動を引き起こす原因でした。仮に\(c<0\)として、第二項を正としても、今度は第三項が負になってしまいます。中心差分法は風上差分法と異なりクーラン数がどんな値を取ろうが右辺に負の項が発生してしまうのです。このため移流方程式の解法において、中心差分法は風上差分法よりもさらに不安定な解法といってよいでしょう。
風下差分法は?
ついでに風下差分(とはあまり呼ばず前進差分と呼ぶことが多いらしいですが…)についても少し触れておきましょう。風下差分は移流の進行方向と同じ方向に差分を取るので以下のように書けます。
\frac{q^{n+1}_{j}-q^{n}_{j}}{\Delta t}&+c\frac{q_{j+1}^{n}-q_{j}^{n}}{\Delta x}= 0\\
\Leftrightarrow
q^{n+1}_{j}&= q^{n}_{j}-\frac{c\Delta t }{\Delta x}\left( q_{j+1}^{n}-q_{j}^{n}\right)\\
&= q^{n}_{j}-\nu q_{j+1}^{n}+\nu q_{j}^{n}\\
&= -\nu q_{j+1}^{n}+\left(1+\nu \right)q_{j}^{n} \tag{10}
\end{align}
このとき\(\nu>0(c>0)\)だと、やはり負の係数が生じてしまいます。よって正の移流方向に対して、風下差分法は不安定です。一方で、負の移流方向(\(c<0\))を考え\(-1<\nu<0\)とすれば、式\((10)\)の右辺の係数をすべて正にすることが出来ます。よって負の移流方向に風下差分は安定です。しかし逆にこの時、式\((7)\)より風上差分は不安定となります。(というか移流方向が変わった時点で、風上差分は風下差分となったと言えます。)
つまり移流方向に対して、逆方向(風上側)に差分を取る手法が安定となるわけです。そもそも流れとは上流から下流に伝わっていくものですので、下流側の情報から上流側の情報を決めることが出来ないのは直感的です。
人工粘性
1次精度風上差分はクーラン数を1以下のとき、安定的に計算することが出来ました。一方、中心差分法はク―ラン数によらず無条件で不安定でした。これについてもう少し踏み込んで考えてみます。1次風上差分式\((5)\)は以下のように変形できます。
q^{n+1}_{j}&= q^{n}_{j}-\frac{c\Delta t }{\Delta x}\left( q_{j}^{n}-q_{j-1}^{n}\right)\\
&= q^{n}_{j}-c\Delta t\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta x}+\frac{c}{2}\left(\frac{\Delta t}{\Delta x}\right)(\Delta x^2 )\frac{q_{j+1}^{n}-2q_{j}^{n}+q_{j-1}^{n}}{\Delta x^2}\tag{11}\\
\end{align}
上式の右辺は中心差分法に\(q\)の2階微分項を加えた形です。拡散方程式にもあるように2階微分項は解を拡散させる効果を有します。これにより風上差分法では中心差分法で不安定化してしまう波を拡散によって無理やり押さえ込んでいるものと解釈できます。(ただし、係数として、\(\Delta x^2\)がついているので、2次以上の誤差が入っているだけで、解く対象を拡散方程式そのものにしてしまったわけではありません。)
このように解の振動現象を止めるために導入される拡散項を人工粘性項とよび、様々な移流スキームで活用されています。
Godunov(ゴドノフ)の定理
ここまで各離散化手法の安定性についてみてきました。これらはGodunov(ゴドノフ)の定理として、以下のように一般化されています。
1次元スカラー移流方程式に対して、
q^{n+1}_{j}=\sum_{k}c_{k}q_{j+k}^n \tag{12}
\end{align}
の形の2次精度以上の精度を持つどのようなスキームも解の単調性を維持することはできない。
上記のように\(q^{n+1}\)が\(q_{j+k}\)の線形結合で表される移流スキームを線形移流スキームと呼びます。
「単調性の維持」とは「ある時刻で\(q\)が\(x\)に関して局所的に単調増加(単調減少)していたならば次の時刻ステップも\(q\)は\(x\)に関して単調増加(単調減少)する。」ということです。言いかえれば「増加と減少を行ったり来たりして、新たな数値振動を生じない。」ということになります。
単調性を維持するには、すべての\(c_{k}\)について\(c_{k}≧0\)を満たす必要があります。1次風上差分法は、クーラン数を1以下ととればこれを満たすことが可能ですが、2次精度である中心差分法はクーラン数をどのようにとってもこれを満たすことはできず、単調性が維持できないというわけです。
より高次精度の差分法でも数値振動から逃れられないというのは驚きです。如何に移流スキームの問題が根が深いのかが分かります。この数値振動の対策として、人工粘性を付加したり、流速制限関数と呼ばれる関数を利用したりする対策が取られるようですが、それらは今後の記事でまとめたいと思います。
MATLABコード
今回用いたコードは以下の通りです。
% 初期化
clearvars;
% パラメーター
Lx = 4;% 計算領域
dLx = 0.01;% 要素サイズ
dt = 0.01;
nx = Lx / dLx + 1;% 要素数
c = 1;% 移流速度
t_max = 3;
iter_max = t_max / dt;
dt_pos = 0.01;% 画像出力間隔
% クーラン数
nu = c * dt / dLx;
% 座標の生成
x = 0 : dLx : Lx;
% 配列確保
q_exact = zeros(nx, 1);
q = zeros(nx, 1);
% 初期条件の設定
for i = 1 : nx
if abs(x(i) - 1) <= 10^-6
q_exact(i) = 1;
q(i) = 1;
elseif x(i) < 1
q_exact(i) = 1;
q(i) = 1;
else
q_exact(i) = 0;
q(i) = 0;
end
end
% 移流スキームの選択
method = '1st order UDS';% 1次精度風上差分法
% method = '2nd order CDS';% 2次精度中心差分法
% 時間発展
for iter = 1 : iter_max
time = iter * dt;
q_old = q;
% 解析解
for i = 1 : nx
if abs(x(i) - (1 + c * time)) < 10^-6
q_exact(i) = 1;
elseif x(i) - (1 + c * time) < 0
q_exact(i) = 1;
else
q_exact(i) = 0;
end
end
% 数値解
for i = 2 : nx - 1 % 境界要素は固定として計算は飛ばす。
switch method
case '1st order UDS'
q(i) = q_old(i) - nu * (q_old(i) - q_old(i - 1));% 1次精度風上差分
case '2nd order CDS'
q(i) = q_old(i) - 0.5 * nu * (q_old(i + 1) - q_old(i - 1));% 2次精度中心差分
otherwise
error("選択された手法:" + method + "はサポートしていないです。" + ...
"1st order UDS, 2nd order CDSから選択してください。");
end
% ノイマン境界条件
q(nx) = q(nx - 1);
end
% コマンドウィンドウへの出力
txt = ['iter = ', num2str(iter), ' / ', num2str(iter_max)];
disp(txt);
% 動画保存
if iter == 1
plotconfig(x, q_exact, q, time, dLx, dt, c, nu, method)
filename = [method, ', dt = ', num2str(dt), ', dx = ', num2str(dLx),', c = ', num2str(c),', nu = ', num2str(nu),'.mp4'];
v = VideoWriter(filename, 'MPEG-4');
v.FrameRate = 40;
open(v);
elseif rem(time, dt_pos) == 0
plotconfig(x, q_exact, q, time, dLx, dt, c, nu, method)
frame = getframe(gcf);
writeVideo(v,frame);
end
end
% 動画ファイルを閉じる
close(v);
%% 以下ローカル関数
function [] = plotconfig(x, ue, u, t, dLx, dt, c, nu, method)
% グラフのプロット
h = plot(x, ue, x, u);
% タイトルの設定
title(['time = ', num2str(t, '%.3f')]);
% 軸の設定
ax = gca; % 現在の軸を取得
ax.FontName = 'Times New Roman'; % 軸のフォント設定
ax.FontSize = 12; % 軸のフォントサイズ設定
axis equal;
axis tight;
axis on;
% グラフの枠の太さ設定
ax.LineWidth = 1.2; % 枠線の太さを変更
% 図の設定
fig = gcf; % 現在の図を取得
fig.Color = 'white'; % 背景色の設定
% Y軸の範囲設定
ylim([-0.5 1.5]);
% X軸とY軸のラベル設定
xlabel('$$x$$', 'Interpreter', 'latex', 'FontSize', 14);
ylabel('$$q$$', 'Interpreter', 'latex', 'FontSize', 14);
% 線の太さを設定
h(1).LineWidth = 1.2; % 1つ目の線(ue)の太さ
h(2).LineWidth = 1.2; % 2つ目の線(u)の太さ
% 凡例の設定
legtxt = [method, ', dt = ', num2str(dt), ', dx = ', num2str(dLx),', c = ', num2str(c),', nu = ', num2str(nu)];
legend('exact', legtxt,'Location','southwest')
legend('boxoff')
% 動画作成のおまじない
set(gca, 'nextplot', 'replacechildren');
end
おわりに
今回は1次元移流方程式について1次精度風上差分法と2次精度中心差分法の2手法で計算を行い、安定性を確認しました。移流の数値計算としては最もベーシックな内容でしたが、今までは漠然とした知識が整理できて個人的にはよかったです。次はより高次精度の離散化手法の検証をできればと考えています。今回はこの辺で。ではでは。
参考文献
[1] 藤井孝蔵、立川智章、Pythonで学ぶ流体力学の数値計算法、2020/10/20


