はじめに
前回記事では多項式近似により、以下の空間高次精度化された界面物理量\({}^L\! q_{i+\frac{1}{2}},{}^R\! q_{i+\frac{1}{2}}\)を得ました。
\begin{align}
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+{}^L\delta q_{i+\frac{1}{2}}\tag{1}\\
{}^R\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i+1}-{}^R\delta q_{i+\frac{1}{2}}\tag{2}
\end{align}
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+{}^L\delta q_{i+\frac{1}{2}}\tag{1}\\
{}^R\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i+1}-{}^R\delta q_{i+\frac{1}{2}}\tag{2}
\end{align}
ここで\({}^L\delta q_{i+\frac{1}{2}},{}^R\delta q_{i+\frac{1}{2}}\)は下表で示される空間高次成分です。
しかしながら、上式は\(t \sim t +\Delta t\)の間の変化を考慮しない、すなわち時間に依存しない時間１次精度の定式化でした。そこで今回はこれを考慮する時間高次精度化についてまとめていきます。
界面物理量の時間高次精度化
では界面物理量\({}^L\! q_{i+\frac{1}{2}},{}^R\! q_{i+\frac{1}{2}}\)はどのような時間依存性を持つと考えるのが適切でしょうか？ここで天下り的ではありますが、時間２次精度の界面物理量\({}^L\! q_{i+\frac{1}{2}}^{*},{}^R\! q_{i+\frac{1}{2}}^{*}\)を以下に示します。
\begin{align}
{}^L\! q_{i+\frac{1}{2}}^{*}&=\bar{\cal{q}}_{i}^{n}+{}^L\delta q_{i+\frac{1}{2}}^{n}-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}{}^L\delta q_{i+\frac{1}{2}}^{n}=\bar{\cal{q}}_{i}^{n}+\left(1-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right){}^L\delta q_{i+\frac{1}{2}}^{n}\tag{3}\\
{}^R\! q_{i+\frac{1}{2}}^{*}&=\bar{\cal{q}}_{i+1}-{}^R\delta q_{i+\frac{1}{2}}^{n}-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}{}^R\delta q_{i+\frac{1}{2}}^{n}=\bar{\cal{q}}_{i+1}^{n}-\left(1+\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right){}^R\delta q_{i+\frac{1}{2}}^{n}\tag{4}
\end{align}
{}^L\! q_{i+\frac{1}{2}}^{*}&=\bar{\cal{q}}_{i}^{n}+{}^L\delta q_{i+\frac{1}{2}}^{n}-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}{}^L\delta q_{i+\frac{1}{2}}^{n}=\bar{\cal{q}}_{i}^{n}+\left(1-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right){}^L\delta q_{i+\frac{1}{2}}^{n}\tag{3}\\
{}^R\! q_{i+\frac{1}{2}}^{*}&=\bar{\cal{q}}_{i+1}-{}^R\delta q_{i+\frac{1}{2}}^{n}-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}{}^R\delta q_{i+\frac{1}{2}}^{n}=\bar{\cal{q}}_{i+1}^{n}-\left(1+\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right){}^R\delta q_{i+\frac{1}{2}}^{n}\tag{4}
\end{align}
\(\alpha_{i+\frac{1}{2}}\)はセル界面\(i+\frac{1}{2}\)における移流速度です。上式右辺第一項は空間・時間1次精度項、第二項は空間高次精度項（２次以上）、そして第三項は時間２次精度項を示しています。
式\((3),(4)\)は一般化されており少々理解しづらいので、Beam-Worming法の\({}^L\! q_{i+\frac{1}{2}}\)を例に具体的な意味を考えてみましょう。Beam-Worming法の\({}^L\! q_{i+\frac{1}{2}}\)は表１より次のように表されました。
\begin{align}
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+\frac{1}{2}\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)\tag{5}\\
\end{align}
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+\frac{1}{2}\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)\tag{5}\\
\end{align}
上式は補正量の勾配計算を意識して、次のように書くと理解しやすいです。
\begin{align}
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+\frac{\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)}{\Delta x}\frac{\Delta x}{2}\tag{6}\\
\end{align}
{}^L\! q_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+\frac{\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)}{\Delta x}\frac{\Delta x}{2}\tag{6}\\
\end{align}
ここでタイムステップの半分（\(\frac{\Delta t}{2}\)）だけ時間が進んだ時の補正量\({}^L\! q^{*}_{i+\frac{1}{2}}\)を考えると次のように書けます。
\begin{align}
{}^L\! q^{*}_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+\frac{\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)}{\Delta x}\frac{\Delta x}{2}-\frac{\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)}{\Delta x}\alpha_{i+\frac{1}{2}}\frac{\Delta t}{2}\\
&=\bar{\cal{q}}_{i}+\frac{1}{2}\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)\left(1-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right)\tag{7}\\
\end{align}
{}^L\! q^{*}_{i+\frac{1}{2}}&=\bar{\cal{q}}_{i}+\frac{\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)}{\Delta x}\frac{\Delta x}{2}-\frac{\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)}{\Delta x}\alpha_{i+\frac{1}{2}}\frac{\Delta t}{2}\\
&=\bar{\cal{q}}_{i}+\frac{1}{2}\left(\bar{\cal{q}}_{i}-\bar{\cal{q}}_{i-1}\right)\left(1-\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\right)\tag{7}\\
\end{align}
上式は式\((3)\)そのものです。模式的にグラフ化すると以下のようになります。
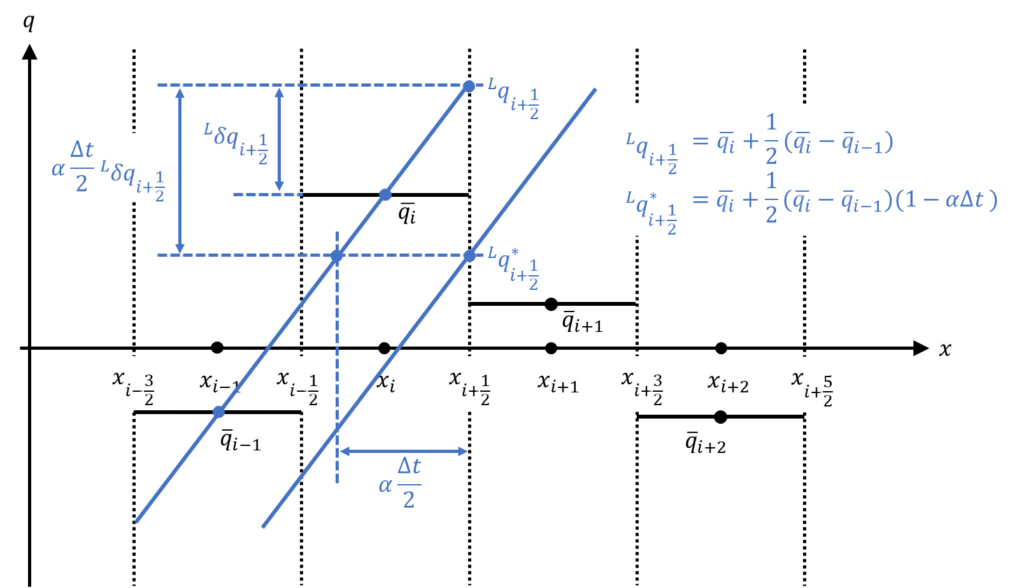
以上より、式\((3),(4)\)は移流速度\(\alpha_{i+\frac{1}{2}}\)でタイムステップの半分\(\left(\frac{\Delta t}{2}\right)\)だけ経過した場合の界面物理量を考えることで、時間精度を上げていることが分かりました。今回は例としてBeam-Worming法を考えましたが、他の手法も同様の考え方が成り立ちます。
数値流束の計算
では実際に式\((3),(4)\)を用いて数値流束を求めてみます。数値流束の計算には以下のRoeリーマンソルバを用いることとします。また簡単のため、移流速度\(\alpha_{i+\frac{1}{2}}=c\)（定数）とし、線形移流方程式を扱うものとします。
\begin{align}
&\tilde{f}_{i+\frac{1}{2}}^{n}＝\tilde{f}({}^R\! q_{i+\frac{1}{2}}^{*},{}^L\! q_{i+\frac{1}{2}}^{*})=\frac{1}{2}\left(f({}^L\! q_{i+\frac{1}{2}}^{*})+f({}^R\! q_{i+\frac{1}{2}}^{*})\right)-\frac{1}{2}\left|\alpha_{i+\frac{1}{2}}\right|({}^R\! q_{i+\frac{1}{2}}^{*}-{}^L\! q_{i+\frac{1}{2}}^{*})
\tag{8} \\
&\alpha_{i+\frac{1}{2}}＝\frac{f({}^R\! q_{i+\frac{1}{2}}^{*})-f({}^L\! q_{i+\frac{1}{2}}^{*})}{{}^R\! q_{i+\frac{1}{2}}^{*}-{}^L\! q_{i+\frac{1}{2}}^{*}}\tag{9}\\
&f(q)＝cq \tag{10} \\
\end{align}
&\tilde{f}_{i+\frac{1}{2}}^{n}＝\tilde{f}({}^R\! q_{i+\frac{1}{2}}^{*},{}^L\! q_{i+\frac{1}{2}}^{*})=\frac{1}{2}\left(f({}^L\! q_{i+\frac{1}{2}}^{*})+f({}^R\! q_{i+\frac{1}{2}}^{*})\right)-\frac{1}{2}\left|\alpha_{i+\frac{1}{2}}\right|({}^R\! q_{i+\frac{1}{2}}^{*}-{}^L\! q_{i+\frac{1}{2}}^{*})
\tag{8} \\
&\alpha_{i+\frac{1}{2}}＝\frac{f({}^R\! q_{i+\frac{1}{2}}^{*})-f({}^L\! q_{i+\frac{1}{2}}^{*})}{{}^R\! q_{i+\frac{1}{2}}^{*}-{}^L\! q_{i+\frac{1}{2}}^{*}}\tag{9}\\
&f(q)＝cq \tag{10} \\
\end{align}
式\((8)\)に式\((3),(4)\)を代入し整理すると最終的に以下の式が得られます。
\begin{align}
\tilde{f}_{i+\frac{1}{2}}^{n}&＝\frac{1}{2}\left[(c-\left|c \right|){}^L\! q_{i+\frac{1}{2}}^{*}+(c+\left|c \right|){}^R\! q_{i+\frac{1}{2}}^{*}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n})+(c+\left|c \right|)(\bar{\cal{q}}_{i+1}^{n}-(1+\nu) {}^R\delta q_{i+\frac{1}{2}}^{n})\right]\tag{11}
\end{align}
\tilde{f}_{i+\frac{1}{2}}^{n}&＝\frac{1}{2}\left[(c-\left|c \right|){}^L\! q_{i+\frac{1}{2}}^{*}+(c+\left|c \right|){}^R\! q_{i+\frac{1}{2}}^{*}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n})+(c+\left|c \right|)(\bar{\cal{q}}_{i+1}^{n}-(1+\nu) {}^R\delta q_{i+\frac{1}{2}}^{n})\right]\tag{11}
\end{align}
式\((5)\)を分解して考えます。なお\(\nu=\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}\)と省略して記載します。
まず第一項を計算します。
\begin{align}
\frac{1}{2}\left(f({}^L\! q_{i+\frac{1}{2}})+f({}^R\! q_{i+\frac{1}{2}})\right)&=\frac{c}{2}\left[\left(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n}\right)+\left(\bar{\cal{q}}_{i+1}^{n}-(1+\nu){}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&=\frac{c}{2}\left[\bar{\cal{q}}_{i}^{n}+\bar{\cal{q}}_{i+1}^{n}+{}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}-\nu\left({}^L\delta q_{i+\frac{1}{2}}^{n}+{}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]
\tag{A1} \\
\end{align}
\frac{1}{2}\left(f({}^L\! q_{i+\frac{1}{2}})+f({}^R\! q_{i+\frac{1}{2}})\right)&=\frac{c}{2}\left[\left(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n}\right)+\left(\bar{\cal{q}}_{i+1}^{n}-(1+\nu){}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&=\frac{c}{2}\left[\bar{\cal{q}}_{i}^{n}+\bar{\cal{q}}_{i+1}^{n}+{}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}-\nu\left({}^L\delta q_{i+\frac{1}{2}}^{n}+{}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]
\tag{A1} \\
\end{align}
次に第二項を計算します。
\begin{align}
-\frac{1}{2}\left|\alpha_{i+\frac{1}{2}}\right|({}^R\! q_{i+\frac{1}{2}}-{}^L\! q_{i+\frac{1}{2}})&=-\frac{\left|c \right| }{2}\left[\left(\bar{\cal{q}}_{i+1}^{n}-(1+\nu){}^R\delta q_{i+\frac{1}{2}}^{n}\right)-\left(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&=-\frac{\left|c \right| }{2}\left[\left(\bar{\cal{q}}_{i+1}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}-\nu{}^R\delta q_{i+\frac{1}{2}}^{n}\right)-\left(\bar{\cal{q}}_{i}^{n}+{}^L\delta q_{i+\frac{1}{2}}^{n}-\nu{}^L\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&=-\frac{\left|c \right| }{2}\left[\bar{\cal{q}}_{i+1}^{n}-\bar{\cal{q}}_{i}^{n}-{}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}+\nu\left({}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]\tag{A2}
\end{align}
-\frac{1}{2}\left|\alpha_{i+\frac{1}{2}}\right|({}^R\! q_{i+\frac{1}{2}}-{}^L\! q_{i+\frac{1}{2}})&=-\frac{\left|c \right| }{2}\left[\left(\bar{\cal{q}}_{i+1}^{n}-(1+\nu){}^R\delta q_{i+\frac{1}{2}}^{n}\right)-\left(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&=-\frac{\left|c \right| }{2}\left[\left(\bar{\cal{q}}_{i+1}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}-\nu{}^R\delta q_{i+\frac{1}{2}}^{n}\right)-\left(\bar{\cal{q}}_{i}^{n}+{}^L\delta q_{i+\frac{1}{2}}^{n}-\nu{}^L\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&=-\frac{\left|c \right| }{2}\left[\bar{\cal{q}}_{i+1}^{n}-\bar{\cal{q}}_{i}^{n}-{}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}+\nu\left({}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]\tag{A2}
\end{align}
式\((A1)\)と式\((A2)\)を足して、式\((8)\)を計算します。
\begin{align}
\tilde{f}_{i+\frac{1}{2}}&＝\frac{c}{2}\left[\bar{\cal{q}}_{i}^{n}+\bar{\cal{q}}_{i+1}^{n}+{}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}-\nu\left({}^L\delta q_{i+\frac{1}{2}}^{n}+{}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&+\frac{\left|c \right| }{2}\left[\bar{\cal{q}}_{i+1}^{n}-\bar{\cal{q}}_{i}^{n}-{}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}+\nu\left({}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}+(c-\left|c \right|){}^L\delta q_{i+\frac{1}{2}}^{n}-(c+\left|c \right|){}^R\delta q_{i+\frac{1}{2}}^{n}-\nu(c-\left|c \right|){}^L\delta q_{i+\frac{1}{2}}^{n}-\nu(c+\left|c \right|) {}^R\delta q_{i+\frac{1}{2}}^{n}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n})+(c+\left|c \right|)(\bar{\cal{q}}_{i+1}^{n}-(1+\nu) {}^R\delta q_{i+\frac{1}{2}}^{n})\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|){}^L\! q_{i+\frac{1}{2}}^{*}+(c+\left|c \right|){}^R\! q_{i+\frac{1}{2}}^{*}\right]\tag{A3}
\end{align}
\tilde{f}_{i+\frac{1}{2}}&＝\frac{c}{2}\left[\bar{\cal{q}}_{i}^{n}+\bar{\cal{q}}_{i+1}^{n}+{}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}-\nu\left({}^L\delta q_{i+\frac{1}{2}}^{n}+{}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&+\frac{\left|c \right| }{2}\left[\bar{\cal{q}}_{i+1}^{n}-\bar{\cal{q}}_{i}^{n}-{}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}+\nu\left({}^L\delta q_{i+\frac{1}{2}}^{n}-{}^R\delta q_{i+\frac{1}{2}}^{n}\right)\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}+(c-\left|c \right|){}^L\delta q_{i+\frac{1}{2}}^{n}-(c+\left|c \right|){}^R\delta q_{i+\frac{1}{2}}^{n}-\nu(c-\left|c \right|){}^L\delta q_{i+\frac{1}{2}}^{n}-\nu(c+\left|c \right|) {}^R\delta q_{i+\frac{1}{2}}^{n}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n})+(c+\left|c \right|)(\bar{\cal{q}}_{i+1}^{n}-(1+\nu) {}^R\delta q_{i+\frac{1}{2}}^{n})\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|){}^L\! q_{i+\frac{1}{2}}^{*}+(c+\left|c \right|){}^R\! q_{i+\frac{1}{2}}^{*}\right]\tag{A3}
\end{align}
以上で式\((11)\)を導出出来ました。
ここで\(\nu=\frac{\alpha_{i+\frac{1}{2}}\Delta t}{\Delta x}=\frac{c\Delta t}{\Delta x}\)と置いています。上式より\(c\)の符号によって数値流束\(\tilde{f}_{i+\frac{1}{2}}\)の計算に左右どちらの界面物理量を用いるかが変化することが分かります。
さらにより具体的にLax-Wendroff法における数値流束を計算してみます。表１にもある通りLax-Wendroff法において高次補正量は以下のように書けました。
\begin{align}
{}^L\delta q_{i+\frac{1}{2}}^{n}={}^R\delta q_{i+\frac{1}{2}}^{n}=\frac{1}{2}(\bar{\cal{q}}_{i+1}^{n}-\bar{\cal{q}}_{i}^{n})\tag{12}
\end{align}
{}^L\delta q_{i+\frac{1}{2}}^{n}={}^R\delta q_{i+\frac{1}{2}}^{n}=\frac{1}{2}(\bar{\cal{q}}_{i+1}^{n}-\bar{\cal{q}}_{i}^{n})\tag{12}
\end{align}
上式を式\((11)\)に代入します。
\begin{align}
\tilde{f}_{i+\frac{1}{2}}^{n}&＝\frac{1}{2}\left[(c-\left|c \right|)(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n})+(c+\left|c \right|)(\bar{\cal{q}}_{i+1}^{n}-(1+\nu) {}^R\delta q_{i+\frac{1}{2}}^{n})\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n})+(c+\left|c \right|)(\bar{\cal{q}}_{i+1}^{n}-(1+\nu) {}^L\delta q_{i+\frac{1}{2}}^{n})\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}+(c-\left|c \right|)(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n}-(c+\left|c \right|)(1+\nu) {}^L\delta q_{i+\frac{1}{2}}^{n}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}+\left\{(c-\left|c \right|)(1-\nu)-(c+\left|c \right|)(1+\nu)\right\} {}^L\delta q_{i+\frac{1}{2}}^{n}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}-2\left(c\nu+\left|c \right|\right){}^L\delta q_{i+\frac{1}{2}}^{n}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}-\left(c\nu+\left|c \right|\right)(\bar{\cal{q}}_{i+1}^{n}-\bar{\cal{q}}_{i}^{n})\right]\\
&＝\frac{c}{2}\left[(1-\nu)\bar{\cal{q}}_{i+1}^{n}+(1+\nu)\bar{\cal{q}}_{i}^{n}\right]\tag{13}
\end{align}
\tilde{f}_{i+\frac{1}{2}}^{n}&＝\frac{1}{2}\left[(c-\left|c \right|)(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n})+(c+\left|c \right|)(\bar{\cal{q}}_{i+1}^{n}-(1+\nu) {}^R\delta q_{i+\frac{1}{2}}^{n})\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)(\bar{\cal{q}}_{i}^{n}+(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n})+(c+\left|c \right|)(\bar{\cal{q}}_{i+1}^{n}-(1+\nu) {}^L\delta q_{i+\frac{1}{2}}^{n})\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}+(c-\left|c \right|)(1-\nu){}^L\delta q_{i+\frac{1}{2}}^{n}-(c+\left|c \right|)(1+\nu) {}^L\delta q_{i+\frac{1}{2}}^{n}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}+\left\{(c-\left|c \right|)(1-\nu)-(c+\left|c \right|)(1+\nu)\right\} {}^L\delta q_{i+\frac{1}{2}}^{n}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}-2\left(c\nu+\left|c \right|\right){}^L\delta q_{i+\frac{1}{2}}^{n}\right]\\
&＝\frac{1}{2}\left[(c-\left|c \right|)\bar{\cal{q}}_{i}^{n}+(c+\left|c \right|)\bar{\cal{q}}_{i+1}^{n}-\left(c\nu+\left|c \right|\right)(\bar{\cal{q}}_{i+1}^{n}-\bar{\cal{q}}_{i}^{n})\right]\\
&＝\frac{c}{2}\left[(1-\nu)\bar{\cal{q}}_{i+1}^{n}+(1+\nu)\bar{\cal{q}}_{i}^{n}\right]\tag{13}
\end{align}
以上がLax-Wendroff法における数値流束です。この形は差分法により得られたLax-Wendroff法の数値流束と一致しています（過去の記事参照）。Fromm法やBeamWarming法も同様の考えで、高次精度化することができます。
後は求めた数値流束を以下の線形移流方程式の離散化式に代入することで時間発展を解くことが出来ます。
\begin{align}
&\frac{\bar{q}_{i}^{n+1}-\bar{q}_{i}^{n}}{\Delta t}+\frac{\tilde{f}^n_{i+\frac{1}{2}}-\tilde{f}^n_{i-\frac{1}{2}}}{\Delta x }=0\\
&\rightarrow
\bar{q}_{i}^{n+1}=\bar{q}_{i}^{n}+\frac{\Delta t}{\Delta x }\left(\tilde{f}^n_{i+\frac{1}{2}}-\tilde{f}^n_{i-\frac{1}{2}}\right)\tag{14}\\
\end{align}
&\frac{\bar{q}_{i}^{n+1}-\bar{q}_{i}^{n}}{\Delta t}+\frac{\tilde{f}^n_{i+\frac{1}{2}}-\tilde{f}^n_{i-\frac{1}{2}}}{\Delta x }=0\\
&\rightarrow
\bar{q}_{i}^{n+1}=\bar{q}_{i}^{n}+\frac{\Delta t}{\Delta x }\left(\tilde{f}^n_{i+\frac{1}{2}}-\tilde{f}^n_{i-\frac{1}{2}}\right)\tag{14}\\
\end{align}
MATLABコード
以下に１次元線形移流方程式、および１次元非粘性Bugers方程式について、空間・時間高次精度を考慮して計算するMATLABコードを示します。変数SW1を切り替えるとことで１次元線形移流方程式または１次元非粘性Bugers方程式のいずれかを選択できます。また変数SW2を切り替えることで不連続な初期値分布と連続な初期値分布のいずれかを選択できます。
% 初期化
clearvars;
% パラメーター
i_max = 100; % 格子セル数
XL = -1.0; % 計算領域左端の座標
XR = 1.0; % 計算領域右端の座標
a = 1.0; % 線形移流方程式の移流速度
tstop = 1; % 計算停止時刻
eps = 1; % 高次精度解法のパラメーター
kappa = 1; % 高次精度解法のパラメーター
% 配列定義
i = 0; % セル番号； (i番目セルの左境界の番号はi、右辺境界の番号はi+1とする)
x = zeros(i_max + 1, 1); % セル境界の座標
u = zeros(i_max, 1); % セル平均値 （数値解）
ue = zeros(i_max, 1); % セル平均値 （厳密解）
ul = zeros(i_max + 1, 1); % セル境界左側の変数値
ur = zeros(i_max + 1, 1); % セル境界右側の変数値
f = zeros(i_max + 1, 1); % セル境界の流束
n = 0; % 時間ステップ
t = 0; % 計算時間
% 方程式を選択
% 1:線形移流方程式、2:非粘性Burgers方程式
sw1 = 2;
% 初期値の選択
% 1:不連続な分布、2:滑らかな分布
sw2 = 1;
% メッシュの設定
dx = (XR - XL) / (i_max - 4.0); % 格子間隔 計算領域外に二つずつ余分なセルを準備。周期的境界条件向けの設定
dt = 0.2 * dx; % 時間刻み
x(1) = XL - 2.0 * dx; % 計算領域外の２セルも考慮した座標を振る。
[x, u] = initc(sw2, i_max, x, dx, u); % 計算格子，時間刻み，初期条件を設定する
% 厳密解の計算
ue = exact(sw1, sw2, i_max, ue, x, t, dx);
% メインループ
while t <= tstop
% 時間発展
n = n + 1;
t = t + dt;
% 空間再構築
[ul, ur] = reconstruction_pc(i_max, u, ul, ur, eps, kappa, dt, dx, sw1);
% リーマンソルバー
f = riemann_roe(i_max, f, ul, ur, sw1);
% 時間積分
u = update(i_max, u, dt, dx, f);
% 境界条件
u = bc(i_max, u);
% 厳密解を求める
ue = exact(sw1, sw2, i_max, ue, x, t, dx);
% 時間表示
fprintf("n=%d, t=%f \n", n, t);
% 動画保存
if n == 1
plotconfig(x(1 : end - 1), ue, u, t, eps, kappa)
filename = ['sw1 = ', num2str(sw1, '%.0f'), ', sw2 = ', num2str(sw2, '%.0f'), ', epsilon = ', num2str(eps, '%.0f'), ', kappa = ', num2str(kappa, '%.3f'),'.mp4'];
v = VideoWriter(filename,'MPEG-4');
v.FrameRate = 40;
open(v);
else
plotconfig(x(1 : end - 1), ue, u, t, eps, kappa)
frame = getframe(gcf);
writeVideo(v,frame);
end
end
% 動画ファイルを閉じる
close(v);
%% 以下ローカル関数
% 初期値の設定
function [x, u] = initc(sw2, i_max, x, dx, u)
for i = 2 : i_max + 1
x(i) = x(i - 1) + dx;% 格子点の座標
end
switch sw2
case 1 % 初期の変数値（滑らかな分布）
for i = 1 : i_max
u(i) = 0.1;
end
for i = i_max / 2 - 10 : i_max / 2 + 10
u(i) = 1.0;
end
case 2 % 初期の変数値（不連続な分布）
for i = 1 : i_max
u(i) = 0.5*(1.1 + sin(2.* pi *(x(i)-x(3))));% 三番目の要素（XL、XRの座標値）を基準に考える。
end
end
end
% 厳密解の計算(不連続分布)
function [ue] = exact(sw1, sw2, i_max, ue, x, t, dx)
switch sw2
case 1 % 不連続分布
switch sw1
case 1 % 線形移流方程式
alpha_12 = 1;% 移流速度
xc = alpha_12 * t;
xl = xc - dx * 10;% 中央に対して10要素だけマイナスに移動した位置
% 周期境界条件
if xl > 1.0
xl = -2.0 + xl;
end
xr = xc + dx * 10.;
% 周期境界条件
if xr > 1.0
xr = -2.0 + xr;
end
if xl <= xr
for i = 1 : i_max
ue(i) = 0.1;
if dx * (i - i_max / 2) >= xl && dx * (i - i_max / 2) <= xr
ue(i) = 1.0;
end
end
end
if xl >= xr
for i = 1 : i_max
ue(i) = 1.0;
if dx * (i - i_max / 2) >= xr && dx * (i - i_max / 2) <= xl
ue(i) = 0.1;
end
end
end
case 2 % 非粘性burgers方程式
xc = - dx * 10 + t;
xl = - dx * 10 + 0.1 * t;
xr = dx * 10 + 0.55 * t;
% 周期境界条件
if xl > 1.0
xl = -2.0 + xl;
end
% 周期境界条件
if xr > 1.0
xr = -2.0 + xr;
end
% 周期境界条件
if xc > 1.0
xc = -2.0 + xc;
end
for i = 1 : i_max
if x(i) <= xl
ue(i) = 0.1;
end
if x(i) >= xl && x(i) <= xc
ue(i) =(x(i) - xl) / (xc - xl) * 0.9 + 0.1;
end
if x(i) >= xc && x(i) <= xr
ue(i) = 1.0;
end
if x(i) >= xr
ue(i) = 0.1;
end
end
end
case 2 % 連続分布
switch sw1
case 1 % 線形移流方程式
alpha_12 = 1; % 移流速度
for i = 1 : i_max
ue(i) = 0.5 * (1.1 + sin(2. * pi * ((x(i) - x(3)) - alpha_12 * t)));
end
case 2 % 非粘性burgers方程式
for i = 1 : i_max
c = 2 * pi;
f = ue(i) - 0.5 * (1.1 + sin(c * (x(i)-x(3) - ue(i) * t)));
df = 1.0 + 0.5 * c * cos(c *(x(i) - x(3) - ue(i) * t)) * t;
count = 0;
while abs(f) >= 1.0e-6
count = count + 1;
ue(i) = ue(i) - f / df; % ニュートン法の計算式*/
f = ue(i) - 0.5 * (1.1 + sin(c*((x(i) - x(3) - ue(i) * t))));
df = 1.0 + 0.5 * c * cos(c * ((x(i) - x(3) - ue(i) * t))) * t;
if count > 10000
disp("厳密解が収束しないので反復を打ち切ります。");
break
end
end
end
end
end
end
function [ul, ur] = reconstruction_pc(i_max, u, ul, ur, eps, kappa, dt, dx, sw1)
for i = 2 : i_max - 2
dul = eps * (0.25 * (1 - kappa) * (u(i) - u(i - 1))...
+ 0.25 * (1 + kappa) * (u(i + 1) - u(i)) );
dur = eps *(- 0.25 * (1 + kappa) * (u(i + 1) - u(i))...
- 0.25 * (1 - kappa) * (u(i + 2) - u(i + 1)));
if sw1 == 1
alpha_12 = 1;
else
alpha_12 = 0.5 * (u(i) + u(i + 1) + dul - dur);
end
ul(i + 1) = u(i) + (1 - alpha_12 * dt / dx) * dul ; % セル境界(i+1/2)左側の値
ur(i + 1) = u(i + 1) - (1 - alpha_12 * dt / dx) * dur; % セル境界(i+1/2)右側の値
end
end
function [f] = riemann_roe(i_max, f, ul, ur, sw1) % 流束を計算する
% 移流速度の計算
switch sw1
case 1 % 線形移流方程式の数値流束
for i = 3 : i_max - 1
alpha_12 = 1;% 移流速度
f_flux_ul = alpha_12 * ul(i);
f_flux_ur = alpha_12 * ur(i);
f(i) = 1.0 / 2.0 * (f_flux_ul + f_flux_ur) - 1.0 / 2.0 * abs(alpha_12) * (ur(i) - ul(i));
end
case 2 % 非粘性burgers方程式の数値流束
for i = 3 : i_max - 1
alpha_12 = 0.5 * (ur(i) + ul(i));% 移流速度
f_flux_ul = 0.5 * ul(i) * ul(i);
f_flux_ur = 0.5 * ur(i) * ur(i);
f(i) = 1.0 / 2.0 * (f_flux_ul + f_flux_ur) - 1.0 / 2.0 * abs(alpha_12) * (ur(i) - ul(i));
end
end
end
function [u] = update(i_max, u, dt, dx, f)
for i = 3 : i_max - 2
u(i) = u(i) - dt / dx * (f(i + 1) - f(i));% 計算変数を更新する
end
end
function [u] = bc(i_max, u) % 周期境界条件
u(1) = u(i_max - 3); % 計算領域左端の境界条件
u(2) = u(i_max - 2); % 計算領域左端の境界条件
u(i_max - 1) = u(3); % 計算領域右端の境界条件
u(i_max) = u(4); % 計算領域右端の境界条件
end
function [] = plotconfig(x, ue, u, t, eps, kappa)
plot(x, ue, x, u)
%plot(x, u)
title(['time = ', num2str(t, '%.3f')]);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 12);
axis equal;
axis tight;
axis on;
fig=gcf;
fig.Color='white';
ylim([-0.2 1.5]);
xlabel('x')
ylabel('u')
% 凡例
method = ['\epsilon = ', num2str(eps, '%.0f'), ', \kappa = ', num2str(kappa, '%.3f')];
legend({'exact', method},'Location','southwest','FontSize', 10)
% 新しいプロットの時、軸設定を保持したまま前のグラフィックスオブジェクトを消去
set(gca,'nextplot','replacechildren');
end
実行結果
以下に線形移流方程式の計算結果を示します。まず\(\epsilon=1,\kappa=1\)の結果です。この場合、空間２次+時間２次精度のLax-Wendroff法になります。
比較のため、前回記事で計算した空間2次+時間１次精度の場合のLax-Wendroff法の結果も以下に示します。
両者を比較すると、時間を２次精度まで考慮したことで、発散が抑えられていることが分かります。これは時間２次精度項が数値粘性として働いているためと考えられます。
さらに\(\epsilon=1,\kappa=\frac{1}{3}\)の場合の結果を示します。この場合、空間３次+時間２次精度です。Lax-Wendroff法と比較して、さらに元の形状を保つことが出来ることが分かります。
おわりに
今回は空間高次精度に加え時間高次精度も考慮した有限体積法による移流方程式の解法をまとめました。線形スキームはあまりよくないかなと思っていましたが、空間３次+時間２次精度（\(\epsilon=1,\kappa=\frac{1}{3}\)）まで考慮すると結構元の形状を保てて少し驚きました。次回はさらなる改善に向け非線形スキームであるTVD法についてまとめていきたいと思います。
参考文献
[1] 肖 鋒, “数値流体解析の基礎- Visual C++とgnuplotによる圧縮性・非圧縮性流体解析 -“, コロナ社, 2020
コメント