はじめに
非構造格子は構造格子と比べて、高い形状再現性を有し、局所メッシュの細分化にも対応可能であるという利点を有しています。私自身もCAE業務でよく使いますが、専門書ではあまり詳しく説明されていないことが多く、情報収集で苦労していました。今回、拡散方程式を例題として基本事項について改めて勉強したのでまとめておきます。
非構造格子の特徴
非構造格子とは、セル(要素)の配置が規則的ではなく、明確な行列インデックスに従わない格子構造を指します。これに対し、構造格子はセルが規則正しく並び、行列のインデックスで自然に管理できるという特徴があります。それぞれに利点と欠点があり、用途に応じた使い分けが重要です。
非構造格子の最大の利点は、その柔軟性にあります。セル配置が不規則なため、構造格子では表現が難しい複雑な形状や曲面にも対応しやすく、複雑なジオメトリを必要とする解析で威力を発揮します。
さらに、非構造格子はメッシュの局所的な細分化や、計算結果に応じた動的なメッシュ変更(アダプティブメッシング)にも適しています。もともと不規則な構造をしているため、構造格子のように全体のインデックス構造を大きく変更する必要がなく、比較的容易にこれらに対応できます。
一方で、非構造格子には管理や計算の面でいくつかの課題があります。セル配置が不規則なため、各セルの番号付けや隣接関係(コネクティビティ)を個別に管理しなければならず、データ構造が煩雑になります。その結果、メモリ管理やアルゴリズムの実装が複雑化し、処理効率が低下することがあります。また、セルの中心点も不規則に分布するため、空間精度を高める高次スキームの適用が難しいという弱点もあります。
このように、構造格子と非構造格子は一長一短であり、解析対象の形状や求める精度・柔軟性に応じて適切に選択することが重要です。

拡散方程式の離散化
では実際に非構造格子に基づき、拡散方程式を離散化していきます。2次元拡散方程式は次式にて与えられました。
\frac{\partial q}{\partial t}&= D\left(\frac{\partial^2 q}{\partial x^2}+\frac{\partial^2 q}{\partial y^2}\right)\\
&= D\mathrm{div} \left(\mathrm{grad} \,q\right)\tag{1}
\end{align}
ここで:
- \(C_{l}\):液相の濃度
- \(D\):拡散係数(定数)
有限体積法で離散化するため、上式についてセル\(i\)の単一セル空間、微小時間に関して平均化します。
\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}&\int_{CV_{i}}\left(\frac{\partial q}{\partial t}\right)dVdt=\frac{D}{\Delta V \Delta t} \int_{t}^{t+\Delta t}\int_{CV_{i}} \mathrm{div} \left(\mathrm{grad}\, q\right)dVdt\tag{2}
\end{align}
ここで、今回は2次元を考えているので、\(z\)方向は有限の厚み\(\delta\)とし、\(dV=\delta dxdy\)と置くこととします。
まずは式\((2)\)の左辺から計算します。
(式(2)左辺)&=\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int_{CV_{i}}\left(\frac{\partial q}{\partial t}\right)dVdt\\
&= \frac{1}{\Delta t}\frac{\partial }{\partial t}\int_{t}^{t+\Delta t} \frac{1}{\Delta V}\left(\int_{CV_{i}}qdV\right)dt
\\
&= \frac{1}{\Delta t}\frac{\partial }{\partial t}\int_{t}^{t+\Delta t}\bar{q}_{i}dt\\
&= \frac{1}{\Delta t}\left[\bar{q}_{i}(t)\right]_{t}^{t+\Delta t}\\
&= \frac{\bar{q}_{i}(t+\Delta t)-\bar{q}_{i}(t)}{\Delta t}\\
&= \frac{\bar{q}_{i}^{n+1}-\bar{q}_{i}^{n}}{\Delta t}
\tag{3}
\end{align}
ここで、2行目から3行目の式変形には以下の有限体積法のセル平均値の定義式を用いました。
\bar{q}_{i}(t)=\frac{1}{\Delta V}\left(\int_{CV_{i}}q\left(x,y,t\right)dV\right)
\tag{4}
\end{align}
次に式\((2)\)の右辺について計算します。ガウスの発散定理を用いて、発散の体積分を面積分へと変換します。
(式(2)右辺)&=\frac{1}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int_{CV_{i}}\mathrm{div} \left( D\mathrm{grad}\, q\right)dVdt\\
&=\frac{D}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int\mathrm{grad}\, q\cdot \boldsymbol{n}dSdt
\tag{5}
\end{align}
ここまでの式変形は構造格子と非構造格子で同じですが、ここからは異なります。今、下図に示すようなセル1~4の4つの三角形からなる小規模な非構造格子を考えます。セル中心は各三角形の重心に定義し、セル1の各辺はセル2~4の1辺と共有しているものとします。
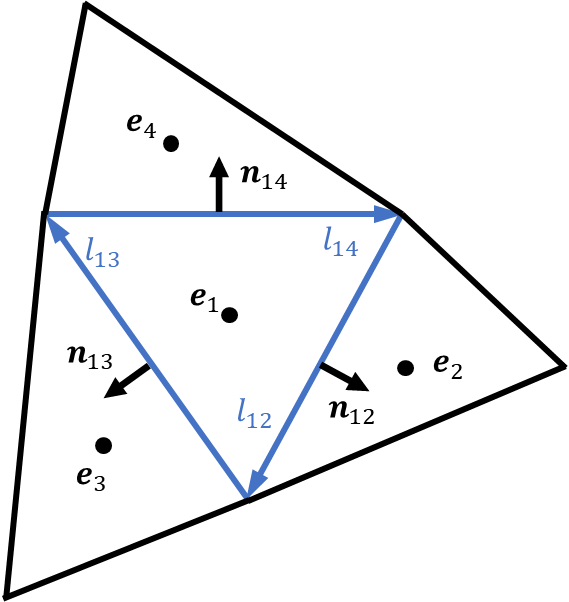
ここで:
- \(e_{i}\):\(i\)番目のセルの重心
- \(l_{i,j}\):\(i\)番目と\(j\)番目のセルが共有する辺ベクトル(向きは任意)
- \(n_{i,j}\):\(l_{i,j}\)の法線ベクトル(向きはセル中心から外側)
以上のような非構造格子において式\((5)\)は次のように変形できます。
&=\frac{D}{\Delta V \Delta t}\int_{t}^{t+\Delta t}\int \left\{\left(\mathrm{grad}\, q\right)_{12}\cdot \boldsymbol{n}_{12}dS_{12}+\left(\mathrm{grad}\, q\right)_{13}\cdot \boldsymbol{n}_{13}dS_{13}+\left(\mathrm{grad}\, q\right)_{14}\cdot \boldsymbol{n}_{14}dS_{14}\right\}dt\\
&=\frac{D\delta}{\Delta V \Delta t}\int_{t}^{t+\Delta t} \left\{\left(\mathrm{grad}\, q\right)_{12}\cdot \boldsymbol{n}_{12}|\boldsymbol{l}_{12}|+\left(\mathrm{grad}\, q\right)_{13}\cdot \boldsymbol{n}_{13}|\boldsymbol{l}_{13}|+\left(\mathrm{grad}\, q\right)_{14}\cdot \boldsymbol{n}_{14}|\boldsymbol{l}_{14}|\right\}dt
\tag{6}
\end{align}
\(t\sim t+\Delta t\)間の時間変化を考慮しない時間一次精度として考えると、中括弧内は時間積分の外に出すことでき、次のように変形できます。
&=\frac{D\delta}{\Delta V } \left\{\left(\mathrm{grad}\, q\right)_{12}\cdot \boldsymbol{n}_{12}|\boldsymbol{l}_{12}|+\left(\mathrm{grad}\, q\right)_{13}\cdot \boldsymbol{n}_{13}|\boldsymbol{l}_{13}|+\left(\mathrm{grad}\, q\right)_{14}\cdot \boldsymbol{n}_{14}|\boldsymbol{l}_{14}|\right\}\\
&=\frac{D}{S_{1}} \left\{\left(\mathrm{grad}\, q\right)_{12}\cdot \boldsymbol{n}_{12}|\boldsymbol{l}_{12}|+\left(\mathrm{grad}\, q\right)_{13}\cdot \boldsymbol{n}_{13}|\boldsymbol{l}_{13}|+\left(\mathrm{grad}\, q\right)_{14}\cdot \boldsymbol{n}_{14}|\boldsymbol{l}_{14}|\right\}
\tag{7}
\end{align}
ここで:
- \(S_{i}\):\(i\)番目のセルの面積
2行目の式変形では\(\Delta V =S_{1}\delta\)を用いました。上式を計算するには、各セル界面ごとの法線ベクトル\(n\)、勾配ベクトル\(\mathrm{grad}\, q\)が必要となります。次節より一つずつ計算していきましょう。
法線ベクトル\(\boldsymbol{n}\)の計算
法線ベクトル\(\boldsymbol{n}\)はノード間ベクトル\(\boldsymbol{l}\)を90度回転させることで計算します。
\boldsymbol{n}_{12}&=
\begin{pmatrix}
\cos 90^\circ & -\sin 90^\circ \\
\sin 90^\circ & \cos 90^\circ
\end{pmatrix}
\frac{\boldsymbol{l}_{12}}{|\boldsymbol{l}_{12}|}\\
&=
\begin{pmatrix}
0& -1 \\
1 & 0
\end{pmatrix}
\frac{\boldsymbol{l}_{12}}{|\boldsymbol{l}_{12}|}
\tag{8}
\end{align}
ただし、このままだと\(\boldsymbol{n}_{12}\)がセル界面外向きか内向きか分からないので、セル中心間を結んだベクトル\(\boldsymbol{d}_{12}\)と内積をとり、負であればマイナス符号をかけて正にすることで、外向きにする処理を加えます。
\begin{equation}
\boldsymbol{n}_{12}=
\begin{cases}
\boldsymbol{n}_{12}& \boldsymbol{n}_{12}\cdot \boldsymbol{d}_{12} >0 \\
-\boldsymbol{n}_{12} & \boldsymbol{n}_{12}\cdot \boldsymbol{d}_{12} <0
\end{cases}
\tag{9}
\end{equation}
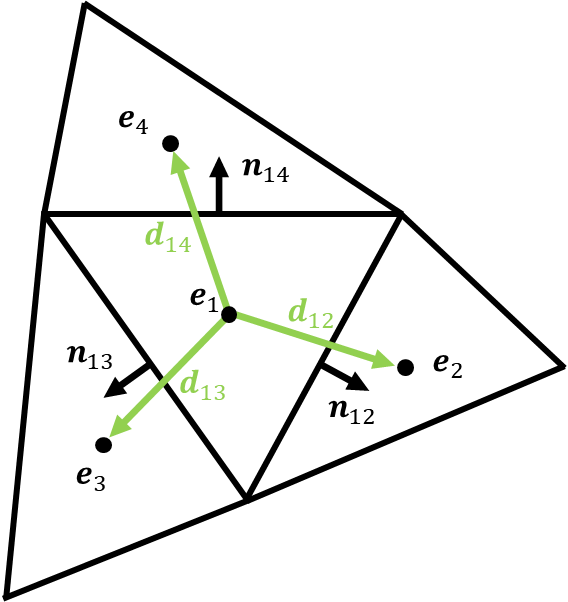
ここで:
- \(d_{i,j}\):\(i\)番目のセル中心から\(j\)番目のセル中心へ向かうベクトル
勾配ベクトル\(\mathrm{grad}\, q\)の計算
勾配ベクトル\(\mathrm{grad}\, q\)は物理量のセル平均値\(\bar{q}\)とセル中心間を結んだベクトル\(\boldsymbol{d}\)を用いて次のように計算されます。
\left(\mathrm{grad}\, q\right)_{12}&=
\frac{\bar{q}_{2}-\bar{q}_{1}}{|d_{12}|}\boldsymbol{d}_{12}
\tag{10}
\end{align}
時間発展式の構築
以上、式\((8)\sim(10)\)を式\((7)\)へ代入すると次式が得られます。
&=\frac{D}{S_{1}} \left\{\frac{\bar{q}_{2}-\bar{q}_{1}}{|\boldsymbol{d}_{12}|}\boldsymbol{d}_{12}\cdot \boldsymbol{n}_{12}|\boldsymbol{l}_{12}|+\frac{\bar{q}_{3}-\bar{q}_{1}}{|\boldsymbol{d}_{13}|}\boldsymbol{d}_{13}\cdot \boldsymbol{n}_{13}|\boldsymbol{l}_{13}|+\frac{\bar{q}_{4}-\bar{q}_{1}}{|\boldsymbol{d}_{14}|}\boldsymbol{d}_{14}\cdot \boldsymbol{n}_{14}|\boldsymbol{l}_{14}|\right\}\\
&=\frac{1}{S_{1}} \left\{\left(\bar{q}_{2}-\bar{q}_{1}\right)k_{12}+\left(\bar{q}_{3}-\bar{q}_{1}\right)k_{13}+\left(\bar{q}_{4}-\bar{q}_{1}\right)k_{14}\right\}
\tag{11}
\end{align}
ここで:
- \(k_{12}=D \left\{\frac{1}{|\boldsymbol{d}_{12}|}\boldsymbol{d}_{12}\cdot \boldsymbol{n}_{12}|\boldsymbol{l}_{12}|\right\}\)
- \(k_{13}=D \left\{\frac{1}{|\boldsymbol{d}_{13}|}\boldsymbol{d}_{13}\cdot \boldsymbol{n}_{13}|\boldsymbol{l}_{13}|\right\}\)
- \(k_{14}=D \left\{\frac{1}{|\boldsymbol{d}_{14}|}\boldsymbol{d}_{14}\cdot \boldsymbol{n}_{14}|\boldsymbol{l}_{14}|\right\}\)
さらに、式\((3)\)を用いると、非構造格子において離散化された拡散方程式は次式にて与えられます。1行目右辺は陰解法で離散化し、タイムステップは\({n+1}\)としていることに注意しましょう。
&\frac{\bar{q}_{1}^{n+1}-\bar{q}_{1}^{n}}{\Delta t}=\frac{1}{S_{1}} \left\{\left(\bar{q}_{2}^{n+1}-\bar{q}_{1}^{n+1}\right)k_{12}+\left(\bar{q}_{3}^{n+1}-\bar{q}_{1}^{n+1}\right)k_{13}+\left(\bar{q}_{4}^{n+1}-\bar{q}_{1}^{n+1}\right)k_{14}\right\}\\
&\Leftrightarrow
S_{1}\bar{q}_{1}^{n+1}- \Delta t\left\{\left(\bar{q}_{2}^{n+1}-\bar{q}_{1}^{n+1}\right)k_{12}+\left(\bar{q}_{3}^{n+1}-\bar{q}_{1}^{n+1}\right)k_{13}+\left(\bar{q}_{4}^{n+1}-\bar{q}_{1}^{n+1}\right)k_{14}\right\}=S_{1}\bar{q}_{1}^{n}\\
&\Leftrightarrow
\left(\begin{array}{cccc}
S_{1}& 0 & 0 & 0
\end{array} \right)
\left(
\begin{array}{c}
\bar{q}_{1}^{n+1} \\
\bar{q}_{2}^{n+1} \\
\bar{q}_{3}^{n+1} \\
\bar{q}_{4}^{n+1} \\
\end{array}
\right)
-\Delta t
\left(\begin{array}{cccc}
-k_{12} -k_{13}-k_{14}
& k_{12} & k_{13} & k_{14}
\end{array} \right)
\left(
\begin{array}{c}
\bar{q}_{1}^{n+1} \\
\bar{q}_{2}^{n+1} \\
\bar{q}_{3}^{n+1} \\
\bar{q}_{4}^{n+1} \\
\end{array}
\right)
\\
&\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad=\left(\begin{array}{cccc}
S_{1}& 0 & 0 & 0
\end{array} \right)
\left(
\begin{array}{c}
\bar{q}_{1}^{n} \\
\bar{q}_{2}^{n} \\
\bar{q}_{3}^{n} \\
\bar{q}_{4}^{n} \\
\end{array}
\right)\\
&\Leftrightarrow
\left\{\left(\begin{array}{cccc}
S_{1}& 0 & 0 & 0
\end{array} \right)
-\Delta t
\left(\begin{array}{cccc}
-k_{12} -k_{13}-k_{14}
& k_{12} & k_{13} & k_{14}
\end{array} \right)\right\}
\left(
\begin{array}{c}
\bar{q}_{1}^{n+1} \\
\bar{q}_{2}^{n+1} \\
\bar{q}_{3}^{n+1} \\
\bar{q}_{4}^{n+1} \\
\end{array}
\right)
\\
&\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad=\left(\begin{array}{cccc}
S_{1}& 0 & 0 & 0
\end{array} \right)
\left(
\begin{array}{c}
\bar{q}_{1}^{n} \\
\bar{q}_{2}^{n} \\
\bar{q}_{3}^{n} \\
\bar{q}_{4}^{n} \\
\end{array}
\right)\\
&\Leftrightarrow
\left\{\boldsymbol{S}
-\boldsymbol{K}\Delta t
\right\}
\bar{\boldsymbol{q}}^{n+1}
=\boldsymbol{S}\bar{\boldsymbol{q}}^{n}
\tag{12}
\end{align}
ここで:
- \(\boldsymbol{S}=\left(\begin{array}{cccc}
S_{1}& 0 & 0 & 0
\end{array} \right)\) - \(\boldsymbol{K}=\left(\begin{array}{cccc}
-k_{12} -k_{13}-k_{14}
& k_{12} & k_{13} & k_{14}
\end{array} \right)\) - \(\bar{\boldsymbol{q}}^{n}=\left(
\begin{array}{c}
\bar{q}_{1}^{n} \\
\bar{q}_{2}^{n} \\
\bar{q}_{3}^{n} \\
\bar{q}_{4}^{n} \\
\end{array}
\right)\)
式\((12)\)はセル1に関する物理量\(\bar{q}_{1}\)の時間発展式です。単体で解くことはできませんが、他のすべてのセルに関して同様に時間発展式を求めることで、連立方程式として解くことが出来ます。
解析条件
次に実際に解析を行います。解析領域は\( – 1<x< 1\) かつ \( -1<y< 1\)とし、一辺\(0.05\)の三角形メッシュで分割します。合計要素数は\(3656\)となりました。
また、初期条件は次式で定義される2次元矩形波を与えることとします。
\bar{\cal{q}}_{i}=
\begin{cases}
1 & \text{$ -0.2 <x< 0.2 \quadかつ \quad -0.2<y< 0.2$} \\
0 & \text{$others$}
\end{cases}
\tag{13}
\end{align}
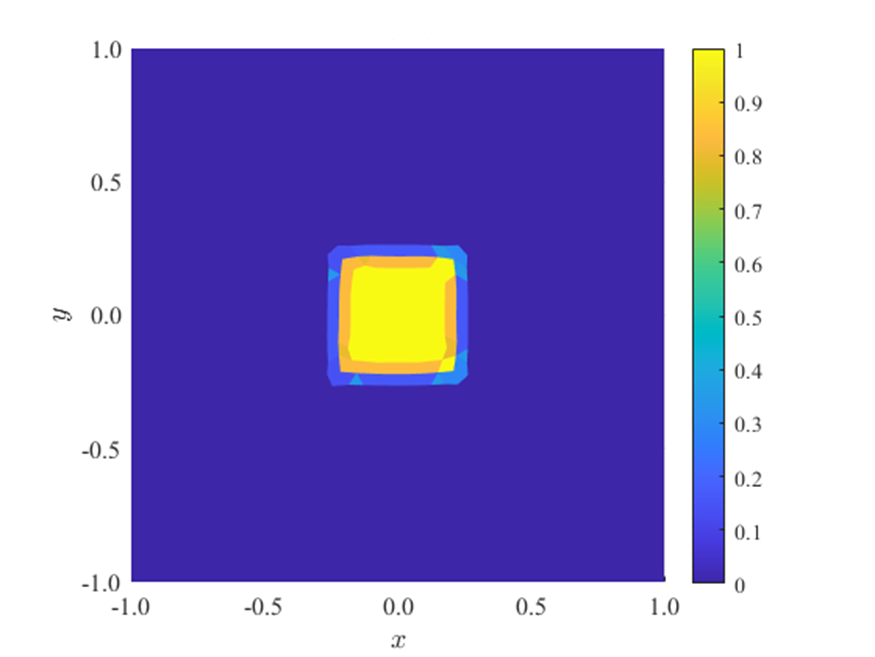
境界条件はいずれもノイマン境界条件(\(\frac{\partial q}{\partial x}=\frac{\partial q}{\partial y}=0\))で与えます。
その他の計算パラメーターは下表にて与えることとします。

解析結果
以下に解析結果のアニメーションを示します。時間とともに矩形波形状が拡散していく様子が確認できます。拡散過程ではメッシュに依存した不自然なムラが見られるようです。メッシュをより細かくすれば改善しますが、同規模の構造格子と比較すると、あまり精度はよくなさそうですね…。
MATLABコード
以下に今回使用したMATLABコードを記載します。実行環境はMATLAB R2022aです。メッシュ生成には「generateMesh」関数などを用いており、実行にはPartial Differential Equation Toolboxが必要です。
clearvars;
%% パラメータ
D = 0.01;
dt = 1e-3;
t_end = 5.0;
steps = ceil(t_end / dt);
frame_rate = 20; % 任意のフレームレートに変更可能
%% メッシュ生成
model = createpde();
geometryFromEdges(model,@squareg);
mesh = generateMesh(model,'Hmax',0.05);
p = mesh.Nodes;
t = mesh.Elements(1:3,:);% 要素を構成する3つのノード番号
[Np, Ne] = deal(size(p,2), size(t,2));
%% メッシュ可視化
figure(1);
pdemesh(model);
% 背景を白に
fig=gcf;
fig.Color='white';
% 軸ラベルやフォント設定
xlabel('$$x$$','Interpreter','latex','FontSize',12);
ylabel('$$y$$','Interpreter','latex','FontSize',12);
set(gca, 'FontName','Times New Roman', 'FontSize',12);
% 軸のアスペクト比・表示範囲の設定
axis('equal');
axis('tight');
% 'TickLabelFormat'を利用してX軸の桁数を指定
ax = gca;
ax.XAxis.TickLabelFormat = '%.1f'; % X軸の桁数を小数点以下2桁に設定
ax.YAxis.TickLabelFormat = '%.1f'; % X軸の桁数を小数点以下2桁に設定
drawnow;
%% 要素重心と面積
centroids = (p(:,t(1,:)) + p(:,t(2,:)) + p(:,t(3,:))) / 3;
area = zeros(Ne,1);
for e = 1:Ne
coords = p(:,t(:,e));% 要素eの3つのノードの座標
area(e) = polyarea(coords(1,:), coords(2,:));
end
%% 初期条件(ある領域の中 = 1, それ以外 = 0)
x_min = -0.2; x_max = 0.2;
y_min = -0.2; y_max = 0.2;
u = double(centroids(1,:) >= x_min & centroids(1,:) <= x_max & ...
centroids(2,:) >= y_min & centroids(2,:) <= y_max)';
%% エッジ情報と面法線ベクトル
[edges, edge2elems, Sf_vec] = build_edges_and_normals(t, p, centroids);
%% ステンシル係数行列 A
A = sparse(Ne, Ne);
for f = 1:size(edges,1)% エッジのループ
e1 = edge2elems(f,1);% エッジに接する要素1
e2 = edge2elems(f,2);% エッジに接する要素2
if e2 == 0, continue; end% エッジに接している要素が一つしかない場合、計算をスキップする。フラックス0となりノイマン条件を満たす。
d_vec = centroids(:,e2) - centroids(:,e1);
len2 = norm(d_vec)^2;
k = D * dot(Sf_vec(:,f), d_vec) / len2;
A(e1,e1) = A(e1,e1) + k;
A(e2,e2) = A(e2,e2) + k;
A(e1,e2) = A(e1,e2) - k;
A(e2,e1) = A(e2,e1) - k;
end
%% 時間積分行列系: (M + dt*A) * u^{n+1} = M * u^n
M = spdiags(area, 0, Ne, Ne);
LHS = M + dt * A;
%% 可視化用(ノード補間)
W = sparse(Np, Ne);
for e = 1:Ne
W(t(:,e), e) = W(t(:,e), e) + 1;
end
node_weights = sum(W,2); node_weights(node_weights==0) = 1;
%% MP4動画保存の初期化
video_filename = 'diffusion_result.mp4';
v = VideoWriter(video_filename, 'MPEG-4');
v.FrameRate = frame_rate;
open(v);
%% 時間発展(陰解法)
draw_interval = 10;
for step = 1:steps
RHS = M * u;
u = LHS \ RHS;
% 可視化(補間 + clip)
if mod(step, draw_interval)==0 || step==steps
figure(2);
u_node = (W * u) ./ node_weights;
u_node = max(u_node, 0);
trisurf(t', p(1,:), p(2,:), u_node(:), 'EdgeColor', 'none');
view(2); colorbar; caxis([0 1]);
title(sprintf('t = %.3f', step*dt));
% 背景を白に
fig=gcf;
fig.Color='white';
% 軸ラベルやフォント設定
xlabel('$$x$$','Interpreter','latex','FontSize',12);
ylabel('$$y$$','Interpreter','latex','FontSize',12);
set(gca, 'FontName','Times New Roman', 'FontSize',12);
% 軸のアスペクト比・表示範囲の設定
axis('equal');
axis('tight');
% 'TickLabelFormat'を利用してX軸の桁数を指定
ax = gca;
ax.XAxis.TickLabelFormat = '%.1f'; % X軸の桁数を小数点以下2桁に設定
ax.YAxis.TickLabelFormat = '%.1f'; % X軸の桁数を小数点以下2桁に設定
drawnow;
frame = getframe(gcf);
writeVideo(v, frame);
end
end
close(v);
fprintf('✅ 動画保存完了: %s\n', video_filename);
function [edges, edge2elems, Sf_vec] = build_edges_and_normals(t, p, centroids)
edge_map = containers.Map('KeyType','char','ValueType','int32');
edges = []; edge2elems_map = containers.Map; edge_count = 0;
Ne = size(t,2);
for e = 1:Ne
nodes = t(:,e);
local_edges = [ ...
[nodes(1); nodes(2)], ...
[nodes(2); nodes(3)], ...
[nodes(3); nodes(1)] ...
];
for k = 1:3
edge = sort(local_edges(:,k));
key = sprintf('%d-%d', edge(1), edge(2));
if ~isKey(edge_map, key)
edge_count = edge_count + 1;
edge_map(key) = edge_count;
edges(edge_count,:) = edge;
edge2elems_map(key) = [e, 0];
else
pair = edge2elems_map(key); pair(2) = e;
edge2elems_map(key) = pair;
end
end
end
Nedges = size(edges,1);
edge2elems = zeros(Nedges,2); Sf_vec = zeros(2,Nedges);
keys = edge_map.keys;
for i = 1:Nedges
key = keys{i}; edge = sscanf(key, '%d-%d');
idx = edge_map(key);
elems = edge2elems_map(key);
edge2elems(idx,:) = elems;
v = p(:,edge(2)) - p(:,edge(1));
normal = [0 -1; 1 0] * v / norm(v);
Sf = norm(v) * normal;
if elems(2) ~= 0
c1 = centroids(:,elems(1)); c2 = centroids(:,elems(2));
if dot(Sf, c2 - c1) < 0, Sf = -Sf; end
end
Sf_vec(:,idx) = Sf;
end
endおわりに
今回は非構造格子で拡散方程式を解きました。実際に実装してみると構造格子と比べてメッシュ管理や流束計算がだいぶ複雑になることが分かりました。今回は拡散方程式でしたが、これが移流方程式になると風上方向を考えたりして、さらにややこしいことになりそうです。非構造格子はCAEで扱うような複雑形状のメッシングには必須ですが、構造格子で済むならそれに越したことはないのでしょうね(精度面でもコスト面でも)。
参考文献
[1] H.K.Versteegら、”数値流体力学 [第2版]”、森北出版, 2011/5/31



コメント