はじめに
前回は１次元移流方程式について、1次精度風上差分法、中心差分法で計算し、解の安定性について検証しました。これらの移流スキームは最もベーシックなもので、より高度なスキームがまだまだたくさんあります。今回はもう一歩踏み込んで、高次の移流スキームである2次精度風上差分法やLax系統の手法についてまとめていきたいと思います。
２次精度風上差分法
前回の記事では、以下の1次元移流方程式について数値解を求めました。
\frac{\partial q}{\partial t}+c\frac{\partial q}{\partial x}= 0\tag{1}
\end{align}
その中で１次精度風上差分法はクーラン数を１以下にすることで安定的に計算できることが分かりました。ではもう一段回精度を引き上げた２次精度風上差分法ならもっとよい結果が得られるのではないでしょうか？２次精度風上差分法は以下の通りに書けます。
\frac{\partial q}{\partial x}=\frac{3q_{j}-4q_{j-1}+q_{j-2}}{2 \Delta x}\tag{2}
\end{align}
\(q=q(x)\)について\(x+\Delta x\)の周りで、テイラー展開すると、以下のように書けます。
q(x+\Delta x)=q(x) + \frac{q(x)^{\prime}}{1!}\Delta x + \frac{q(x)^{\prime\prime}}{2!}\Delta x^2+ \frac{q(x)^{\prime\prime\prime}}{3!}\Delta x^3+\cdots \tag{3}
\end{align}
上式を\(q(x)=q_{j}\)、\(q(x+\Delta x)=q_{j+1}\)のように離散点を用いて書き換えると
q_{j+1}=q_{j} + \Delta x\left.\frac{\partial q}{\partial x}\right|_{j} + \frac{1}{2}(\Delta x)^2\left.\frac{\partial ^2 q}{\partial x^2}\right|_{j} + \frac{1}{6}(\Delta x)^3\left.\frac{\partial ^3 q}{\partial x^3}\right|_{j}+\cdots \tag{4}
\end{align}
\(\Delta x\)を\(-\Delta x\)、\(-2\Delta x\)と考えて式\((4)\)を書き換えると以下の式が得られます。
q_{j-1}=q_{j} – (\Delta x)\left.\frac{\partial q}{\partial x}\right|_{j} + \frac{1}{2}(\Delta x)^2\left.\frac{\partial ^2 q}{\partial x^2}\right|_{j} – \frac{1}{6}(\Delta x)^3\left.\frac{\partial ^3 q}{\partial x^3}\right|_{j}+\cdots \tag{5}
\end{align}
q_{j-2}=q_{j} – (2\Delta x)\left.\frac{\partial q}{\partial x}\right|_{j} + \frac{1}{2}(2\Delta x)^2\left.\frac{\partial ^2 q}{\partial x^2}\right|_{j} – \frac{1}{6}(2\Delta x)^3\left.\frac{\partial ^3 q}{\partial x^3}\right|_{j}+\cdots \tag{6}
\end{align}
式\((5)\)を4倍して式\((6)\)を引くと偶数次数の微分係数の項はすべて消え、式\((2)\)を得ることが出来ます。
&4q_{j-1}-q_{j-2}=3q_{j} – (2\Delta x)\left.\frac{\partial q}{\partial x}\right|_{j} + O(\Delta x^3) \\
&\Leftrightarrow
(2\Delta x)\left.\frac{\partial q}{\partial x}\right|_{j}=3q_{j} -4q_{j-1}+q_{j-2}+ O(\Delta x^3) \\
&\Leftrightarrow
\left.\frac{\partial q}{\partial x}\right|_{j}=\frac{3q_{j} -4q_{j-1}+q_{j-2}}{2\Delta x}+ O(\Delta x^2) \tag{7}
\end{align}
式\((2)\)に基づき式\((1)\)を離散化すると以下のように書けます。
&\frac{q_{j}^{n+1}-q_{j}^{n}}{\Delta t}=-c\frac{3q_{j}^{n}-4q_{j-1}^{n}+q_{j-2}^{n}}{2 \Delta x}\\
&\Leftrightarrow
q_{j}^{n+1}=q_{j}^{n}- \frac{c \Delta t}{2 \Delta x}\left(3q_{j}^{n}-4q_{j-1}^{n}+q_{j-2}^{n}\right)\tag{7}
\end{align}
クーラン数\(\nu=\frac{c \Delta t}{\Delta x}\)を用いて整理します。
&q_{j}^{n+1}=q_{j}^{n}- \frac{\nu}{2}\left(3q_{j}^{n}-4q_{j-1}^{n}+q_{j-2}^{n}\right)\\
&\Leftrightarrow
q_{j}^{n+1}=\left(1- \frac{3\nu}{2}\right)q_{j}^{n}+2\nu q_{j-1}^{n}-\frac{\nu}{2}q_{j-2}^{n}\tag{8}
\end{align}
上記を見ると右辺第三項の係数が負となってしまっています。また第一項の係数もクーラン数が大きくなると負になってしまいます。これらは数値振動の原因となるのでした。
一次風上差分法は安定だったにもかかわらず、高次精度になることでむしろ数値振動を有してしまう点が難しいところです。前回記事で述べた、ゴルドフの定理にもあったとおり、「2次精度以上の精度を持つどのようなスキームも単調性は維持することができない」というわけです。
実際に計算してみます。パラメーターは以下の4パターンとします。
①：\(\Delta t = 0.001, \Delta x = 0.01, c = 1 →\nu = \frac{c\Delta t }{\Delta x}=0.1\)
②：\(\Delta t = 0.005, \Delta x = 0.01, c = 1 →\nu = \frac{c\Delta t }{\Delta x}=0.5\)
③：\(\Delta t = 0.01, \Delta x = 0.01, c = 1 →\nu = \frac{c\Delta t }{\Delta x}=1\)
④：\(\Delta t = 0.02, \Delta x = 0.01, c = 1 →\nu = \frac{c\Delta t }{\Delta x}=2\)
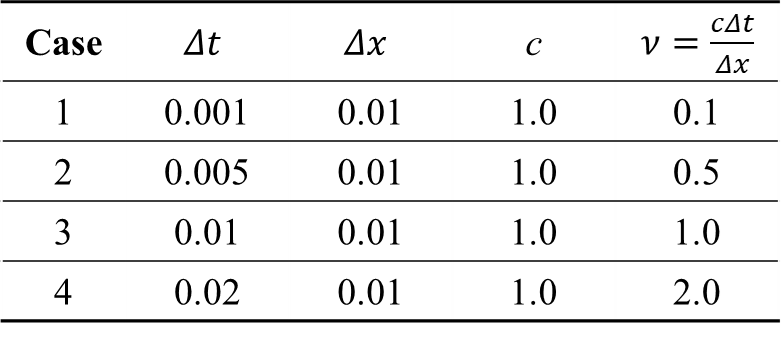
以下が結果のアニメーションです。
クーラン数が0.1程度ならば比較的数値振動を小さく保つことが出来ていますが、0.5を超えると振動が大きくなり元の形状を全く保てなくなっています。この不安定性は如何ともしがたい…。
Lax-Friedrich法
前回記事にて２次精度中心差分法による離散化式は以下のように書けました。
q_{j}^{n+1}=q_{j}^{n}- \frac{c \Delta t}{2 \Delta x}\left(q_{j+1}^{n}-q_{j-1}^{n}\right)\tag{9}
\end{align}
中心差分法は無条件不安定でしたが、空間的に対称な差分形式という点は優れています。Lax-Friedrich法は中心差分法に単純な変更を施すことで空間対称性を維持したまま安定化させるスキームです。
具体的には\(q_{j}^{n}\)を隣接点からの補間として、\(q_{j}^{n}=\frac{1}{2}(q_{j-1}^{n}+q_{j+1}^{n})\)と表して、式\((9)\)を書き換えます。
&q_{j}^{n+1}=\frac{1}{2}(q_{j-1}^{n}+q_{j+1}^{n})- \frac{c \Delta t}{2 \Delta x}\left(q_{j+1}^{n}-q_{j-1}^{n}\right)\\
&\Leftrightarrow
q_{j}^{n+1}=\frac{1}{2}(1+\nu)q_{j-1}^{n}+\frac{1}{2}\left(1-\nu\right)q_{j+1}^{n}\tag{10}\\
\end{align}
上式右辺の係数より\(\nu \leq 1\)で安定に解くことができることが分かります。特に\(\nu＝1\)では風上差分法に一致するので、厳密解を再現可能です。
また式\((10)\)は以下のように変形することができます。
q_{j}^{n+1}=q_{j}^{n}-c\Delta t\frac{q_{j+1}^{n}-q_{j-1}^{n}}{2\Delta x}+\frac{1}{2}(\Delta x^2)\frac{q_{j+1}^{n}-2q_{j}^{n}+q_{j-1}^{n}}{\Delta x^2}\tag{11}\\
\end{align}
上式右辺は中心差分法＋人工粘性項の形となっており、振動的な中心差分に対して、人工粘性項により解の安定化を図っていると解釈できます。この辺りは前回記事で記載した１次風上差分法と同様です。
では実際に計算してみます。パラメーターは上記の２次精度風上差分法の時ど同様です。以下が結果のアニメーションです。
\(\nu \leq 1\)では\(\nu\)が１に近づくにつれて、解が厳密解に近づいていきます。一方、クーラン数が２になると数値振動が激しくなっています。このあたりの挙動は1次精度風上差分法に近いです。またよく見ると滑らかなカーブではなく階段状のカーブとなっているのが特徴です。
Lax-Wendroff法
ここまでのスキームは移流方程式にテイラー展開より得られた差分式を代入することで導出してきました。一方、Lax-Wendroff法は少し毛色が異なり、テイラー展開で得られた式に移流方程式を代入することで得られます。
まず\(q(t+\Delta t)\)に関してテイラー展開を適用すると以下の式が得られます。
q(t+\Delta t)=q(t)+\Delta t \frac{\partial q}{\partial t}+ \frac{1}{2}\Delta t^2 \frac{\partial ^2 q}{\partial t^2}+ O(\Delta t^3)\tag{12}\\
\end{align}
また式\((1)\)より以下の式が得られます。
\frac{\partial q}{\partial t}= -c\frac{\partial q}{\partial x}\tag{13}
\end{align}
&\frac{\partial^2 q}{\partial t^2}= -c\frac{\partial }{\partial t}\left(\frac{\partial q}{\partial x}\right)\\
&\Leftrightarrow
\frac{\partial^2 q}{\partial t^2}= -c\frac{\partial }{\partial x}\left(\frac{\partial q}{\partial t}\right)\\
&\Leftrightarrow
\frac{\partial^2 q}{\partial t^2}= c^2\frac{\partial^2 q}{\partial x^2}\tag{14}
\end{align}
式\((13),(14)\)を式\((12)\)に代入すると以下のように書けます。
&q(t+\Delta t)=q(t)-c\Delta t \frac{\partial q}{\partial x}+ \frac{1}{2}c^2\Delta t^2 \frac{\partial^2 q}{\partial x^2}+ O(\Delta t^3)\\
&\Leftrightarrow
\frac{q(t+\Delta t)-q(t)}{\Delta t}=-c \frac{\partial q}{\partial x}+ \frac{1}{2}c^2\Delta t \frac{\partial^2 q}{\partial x^2}+ O(\Delta t^2)\tag{15}\\
\end{align}
これまでのスキームは時間離散化に１次精度オイラー陽解法を用いてきましたが、上式は時間に関して2次の精度で離散化することが出来ています。
上式の\( \frac{\partial q}{\partial x}、\frac{\partial^2 q}{\partial x^2}\)を2次精度中心差分法で離散化すると以下の式が得られます。
&q_{j}^{n+1}=q_{j}^{n}-c\Delta t \frac{q_{j+1}^{n}-q_{j-1}^{n}}{2\Delta x}+ \frac{1}{2}c^2\Delta t^2 \frac{q_{j+1}^{n}-2q_{j}^{n}+q_{j-1}^{n}}{\Delta x^2}\tag{16}\\
\end{align}
上式がLax-Wendroff法の離散化形式となります。Lax-Wendroff法は空間・時間共に2次精度の解法です。式\((11)\)のLax-Friedrich法と比較すると拡散項の係数が\(\left(\frac{\Delta t}{\Delta x}\right)^ 2\)の分だけ違います。クーラン数が１を超えないことを考えると、Lax-Friedrich法よりもLax-Wendroff法のほうが、拡散の効果が小さいといえるでしょう。
クーラン数を用いて書き換えると以下の通りです。
&q_{j}^{n+1}=q_{j}^{n}-\frac{1}{2}\nu \left(q_{j+1}^{n}-q_{j-1}^{n}\right)+\frac{1}{2}\nu ^2 \left(q_{j+1}^{n}-2q_{j}^{n}+q_{j-1}^{n}\right)\\
&\Leftrightarrow
q_{j}^{n+1}=q_{j}^{n}-\frac{1}{2}\nu q_{j+1}^{n} +\frac{1}{2}\nu q_{j-1}^{n}+ \frac{1}{2}\nu ^2 q_{j+1}^{n}-\nu ^2q_{j}^{n}+\frac{1}{2}\nu ^2q_{j-1}^{n}\\
&\Leftrightarrow
q_{j}^{n+1}=\left( 1-\nu ^2 \right)q_{j}^{n}+\frac{1}{2}\nu\left(\nu – 1\right) q_{j+1}^{n} +\frac{1}{2}\nu \left( 1+ \nu\right) q_{j-1}^{n}
\tag{17}\\
\end{align}
上式は一見するとすべての係数を正とすることはできないように見えます。例えば第一項はクーラン数が１以下ならば正の係数を持ちますが、その場合、第二項は負になってしまいます。ではLax-Wendroff法は無条件不安定といってよいのでしょうか？
ここまでと同様に実際に計算し確認してみます。結果は以下のアニメーションの通りです。
Lax-Friedrich法と同様、\(\nu \leq 1\)では\(\nu\)が１に近づくにつれて、解が厳密解に近づいていきます。また、クーラン数が２になると発散しています。Lax-Friedrich法よりも解は振動を有するものの、拡散の影響は小さいようです。
上記の結果からもわかるようにLax-Wendroff法はクーラン数１以下で安定の手法です。式\((17)\)からそれを読み取るのは難しいようですが、「フォンノイマンの安定性解析」と呼ばれる手法を用いることで証明されます。この辺の話は長くなるので、またいつか機会があればまとめたいと思います。
MATLABコード
今回用いたコードは以下の通りです。githubにもアップしましたのでよろしければご参考ください。
% 初期化
clearvars;
% パラメーター
Lx = 4;% 計算領域
dLx = 0.01;% 要素サイズ
dt = 0.005;
nx = Lx / dLx + 1;% 要素数
c = 1;% 移流速度
t_max = 3;
iter_max = t_max / dt;
dt_pos = 0.02;% 画像出力間隔
% クーラン数
nu = c * dt / dLx;
% 座標の生成
x = 0 : dLx : Lx;
% 配列確保
q_exact = zeros(nx, 1);
q = zeros(nx, 1);
% 初期条件の設定
for i = 1 : nx
if abs(x(i) - 1) <= 10^-6
q_exact(i) = 1;
q(i) = 1;
elseif x(i) < 1
q_exact(i) = 1;
q(i) = 1;
else
q_exact(i) = 0;
q(i) = 0;
end
end
% 移流スキームの選択
method = '1st order UDS';% 1次精度風上差分法
%method = '2nd order CDS';% 2次精度中心差分法
%method = '2nd order UDS';% 2次精度風上差分法
%method = 'Lax-Friedrich';% Lax-Friedrich法
%method = 'Lax-Wendroff';% Lax-Wendroff法
% 時間発展
for iter = 1 : iter_max
time = iter * dt;
q_old = q;
% 解析解
for i = 1 : nx
if abs(x(i) - (1 + c * time)) < 10^-6
q_exact(i) = 1;
elseif x(i) - (1 + c * time) < 0
q_exact(i) = 1;
else
q_exact(i) = 0;
end
end
% 数値解
switch method
case '1st order UDS'
for i = 2 : nx
q(i) = q_old(i) - nu * (q_old(i) - q_old(i - 1));% 1次精度風上差分
end
case '2nd order CDS'
for i = 2 : nx - 1
q(i) = q_old(i) - 0.5 * nu * (q_old(i + 1) - q_old(i - 1));% 2次精度中心差分
end
q(nx) = q(nx - 1);
case '2nd order UDS'
for i = 3 : nx
q(i) = q_old(i) - 0.5 * nu * (3 * q_old(i) - 4 * q_old(i - 1) + q_old(i - 2));% 2次精度中心差分
end
case '3rd order UDS'
for i = 3 : nx - 1
q(i) = q_old(i) - nu * (2 * q_old(i + 1) + 3 * q_old(i) - 6 * q_old(i - 1) + q_old(i - 2)) / 6; % 3次精度中心差分
end
case 'Lax-Friedrich'
for i = 2 : nx - 1
q(i) = 0.5 * (q_old(i + 1) + q_old(i - 1)) - 0.5 * nu * (q_old(i + 1) - q_old(i - 1));% Lax-Friedric
end
q(nx) = q(nx - 1);
case 'Lax-Wendroff'
for i = 2 : nx - 1
q(i) = q_old(i) - 0.5 * nu * (q_old(i + 1) - q_old(i - 1)) + 0.5 * nu^2 * (q_old(i + 1) - 2 * q_old(i) + q_old(i - 1));% 2次精度中心差分
end
q(nx) = q(nx - 1);
otherwise
error("選択された手法：" + method + "はサポートしていないです。" );
end
% コマンドウィンドウへの出力
txt = ['iter = ', num2str(iter), ' / ', num2str(iter_max)];
disp(txt);
% リアルタイム可視化
filename = [method, ', dt = ', num2str(dt), ', dx = ', num2str(dLx),', c = ', num2str(c),', nu = ', num2str(nu),'.gif'];
fignum = 1;
plot(x, q_exact, x, q)
title(['time = ', num2str(time, '%.3f')]);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 12);
axis equal; axis tight; axis on;
fig=gcf;
fig.Color='white';
xlim([0 4]);
ylim([-1 2]);
xlabel('x')
ylabel('q')
legtxt = [method, ', dt = ', num2str(dt), ', dx = ', num2str(dLx),', c = ', num2str(c),', nu = ', num2str(nu)];
legend('exact', legtxt,'Location','southwest')
legend('boxoff')
frame = getframe(fignum);
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if time == dt_pos
imwrite(imind, cm, filename, 'gif', 'DelayTime', 0.05, 'Loopcount', inf);
elseif rem(time, dt_pos) == 0
imwrite(imind, cm, filename, 'gif', 'DelayTime', 0.05, 'WriteMode', 'append');
end
end
おわりに
今回はより高次の線形移流スキームについて紹介しました。今回紹介したもの以外にも高次スキームは様々な手法があります。どれを用いればよいのか迷いますが、線形移流スキームではLax-Wendroff法が比較的実用的なのでしょうか…。ともあれ線形スキームの限界も見えてきた感じがするので、次回からは非線形スキームのほうへ話題を進めたいと思います。
参考文献
[1]藤井孝蔵、立川智章、Pythonで学ぶ流体力学の数値計算法、2020/10/20
[2]松元亮治, 「差分法の基礎」, CANS+ ドキュメント, http://www.astro.phys.s.chiba-u.ac.jp/cans/doc/sabun.html#figlfphase