はじめに
今回も前回に引き続き、VOF法の解説を行っていきます。前回は流れ計算まで説明しました。今回はVOF法のキーポイントであるVOF値の移流部分を説明してきます。
VOF値の計算:基礎方程式
ドナー・アクセプター法に入る前に、基礎方程式を離散化しておきます。実装するのは2次元系ですが、イメージをつかむために一旦3次元系で考えてみます。VOF値\(F\)に関する基礎方程式は移流方程式として以下のように書けました。
\frac{\partial F}{\partial t}+\frac{\partial (Fu)}{\partial x}+\frac{\partial (Fv)}{\partial y}+\frac{\partial (Fw)}{\partial z}=0\tag{1}
\end{align}
式\((1)\)は発散\(div\)を用いた形で表すと以下のようにも書けます。
\frac{\partial F}{\partial t}=-div
\left(F\boldsymbol{u}\right)
\tag{2}
\end{align}
これを単一セル内で体積分し、ガウスの発散定理を用いて変形すると以下の式が得られます。
&\int_{cell}\frac{\partial F}{\partial t}dV_{cell}=-\int_{cell}div
\left(F\boldsymbol{u}\right)dV_{cell}\\
&\Leftrightarrow
\int_{cell}\frac{\partial F}{\partial t}dV_{cell}=-\int_{cell}\left(F\boldsymbol{u}\right)\cdot \boldsymbol{dS_{cell}}\\
&\Leftrightarrow
\frac{\partial }{\partial t}\int_{cell}FdV_{cell}
=-\left[ (Fu)_{+x}dydz-(Fu)_{-x}dydz +(Fv)_{+y}dxdz-(Fv)_{-y}dxdz+(Fw)_{+z}dxdy-(Fw)_{-z}dxdy \right]
\tag{3}
\end{align}
この式の右辺は「単一セルの各表面から流入・流出する正味の液体量」を示しています。
次に上式左辺を離散化します。
&\frac{F_{i,j,k}^{n+1}- F_{i,j,k}^{n}}{dt}dV_{cell}=-\left[ (Fu)_{+x}dydz-(Fu)_{-x}dydz +(Fv)_{+y}dxdz-(Fv)_{-y}dxdz+(Fw)_{+z}dxdy-(Fw)_{-z}dxdy \right]\\
&\Leftrightarrow
F_{i,j,k}^{n+1}
= F_{i,j,k}^{n}-\frac{dt}{dV_{cell}}\left[ (Fu)_{+x}dydz-(Fu)_{-x}dydz +(Fv)_{+y}dxdz-(Fv)_{-y}dxdz+(Fw)_{+z}dxdy-(Fw)_{-z}dxdy \right]\\
&\Leftrightarrow
F_{i,j,k}^{n+1}
= F_{i,j,k}^{n}-\left[ \frac{(Fu)_{+x}dydzdt}{dV_{cell}}- \frac{(Fu)_{-x}dydzdt}{dV_{cell}} + \frac{(Fv)_{+y}dxdzdt}{dV_{cell}}- \frac{(Fv)_{-y}dxdzdt}{dV_{cell}}+ \frac{(Fw)_{+z}dxdydt}{dV_{cell}}- \frac{(Fw)_{-z}dxdydt}{dV_{cell}} \right]
\tag{4}
\end{align}
上式の右辺鍵括弧内は「各セルの体積に対する\(dt\)あたりに流入・流出する液体の体積の比」を示しています。
上式は3次元系の式なので、2次元系に書き換えます。\(w=0\)、\((i,j,k)\Rightarrow(i,j)\)とすればよいので、
&F_{i,j}^{n+1}
= F_{i,j}^{n}-\left[ \frac{(Fu)_{+x}dydzdt}{dV_{cell}}- \frac{(Fu)_{-x}dydzdt}{dV_{cell}} + \frac{(Fv)_{+y}dxdzdt}{dV_{cell}}- \frac{(Fv)_{-y}dxdzdt}{dV_{cell}} \right]\\
&\Leftrightarrow
F_{i,j}^{n+1}
= F_{i,j}^{n}-\left[ \frac{(Fu)_{+x}dydzdt}{dxdydz}- \frac{(Fu)_{-x}dydzdt}{dxdydz} + \frac{(Fv)_{+y}dxdzdt}{dxdydz}- \frac{(Fv)_{-y}dxdzdt}{dxdydz} \right]\\
&\Leftrightarrow
F_{i,j}^{n+1}
= F_{i,j}^{n}-\left[ \frac{(Fu)_{+x}dt}{dx}- \frac{(Fu)_{-x}dt}{dx} + \frac{(Fv)_{+y}dt}{dy}- \frac{(Fv)_{-y}dt}{dy} \right]
\tag{5}
\end{align}
最後に右辺鍵括弧内を\(DFU,DFV\)と表し、以下図のように流速と同じセル境界位置で離散化することとします。
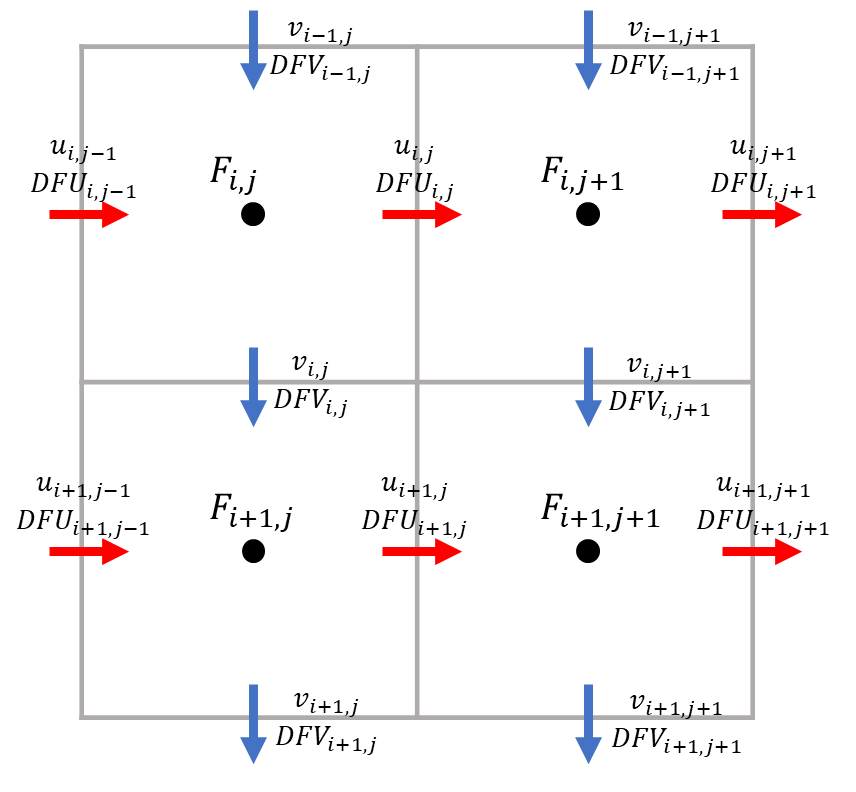
すると式\((5)\)は以下のように書けます。
F_{i.j}^{n+1}=F_{i.j}^{n}-\left( DFU_{i,j}- DFU_{i,j-1}+DFV_{i,j}-DFV_{i-1,j}\right)
\tag{6}
\end{align}
以上が今回利用する移流方程式の離散化形式となります。
上記のような移流方程式は通常は風上差分法やTVD系スキームといったNS法方程式で用いられるような移流解法で解かれます。しかしながら、これらの解法は数値拡散により、液体を消失させてしまうという問題を引き起こします。具体例として以下に風上差分でダムブレイクを計算した例を示します。
上の動画からあっという間に水面が拡散し、液体がなくなってしまう様子が確認できます。これではとても液体挙動は計算できません。このような問題に対し提案されたのが、次から記載するドナー・アクセプター法です。
VOF値の計算:ドナー・アクセプター法
ドナー・アクセプター法はVOF値が0~1の範囲であることを利用して、物理的考察に基づき、ある種のルールベースで移流の量・方向を決める手法です。偏微分方程式を直接的に解きに行くわけではないので、数値粘性による水面の拡散を防止することが出来ます。
この方法では隣り合うセルをその間で定義される流速の符号によって、流体を送りだすセル(ドナーセル)と流体を受け取るセル(アクセプターセル)に分類し、各セルの属性情報(界面、液体、空気)の組み合わせから移流量を決定します。順に具体例を見ていきます。
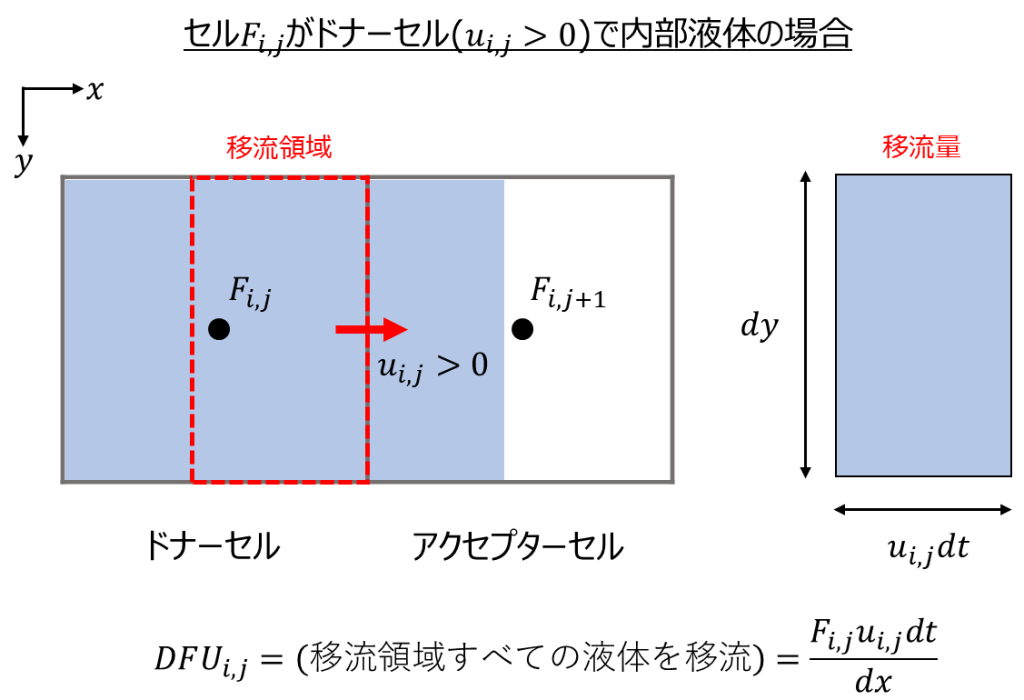
例えば、\(u_{i,j}>0\)の時、\(F_{i.j}\)のセルがドナーセル、\(F_{i.j+1}\)のセルがアクセプターセルとなります。この時、ドナーセル\(F_{i.j}\)が内部液体の場合、\(x\)方向への移流量\(DFU_{i,j}\)は以下のように書けます。
(移流領域内の液体存在面積):(移流量)&=(セル内の液体存在面積):(液体体積率)\\
\Leftrightarrow
u_{i,j}dtdy:DFU_{i,j}&=dxdy:F_{i,j}\\
\Leftrightarrow
DFU_{i,j}&=\frac{F_{i,j}u_{i,j}dt}{dx}\\
\tag{7}
\end{align}
この場合、内部が液体で満ちているので比較的シンプルに移流量を表現できます。
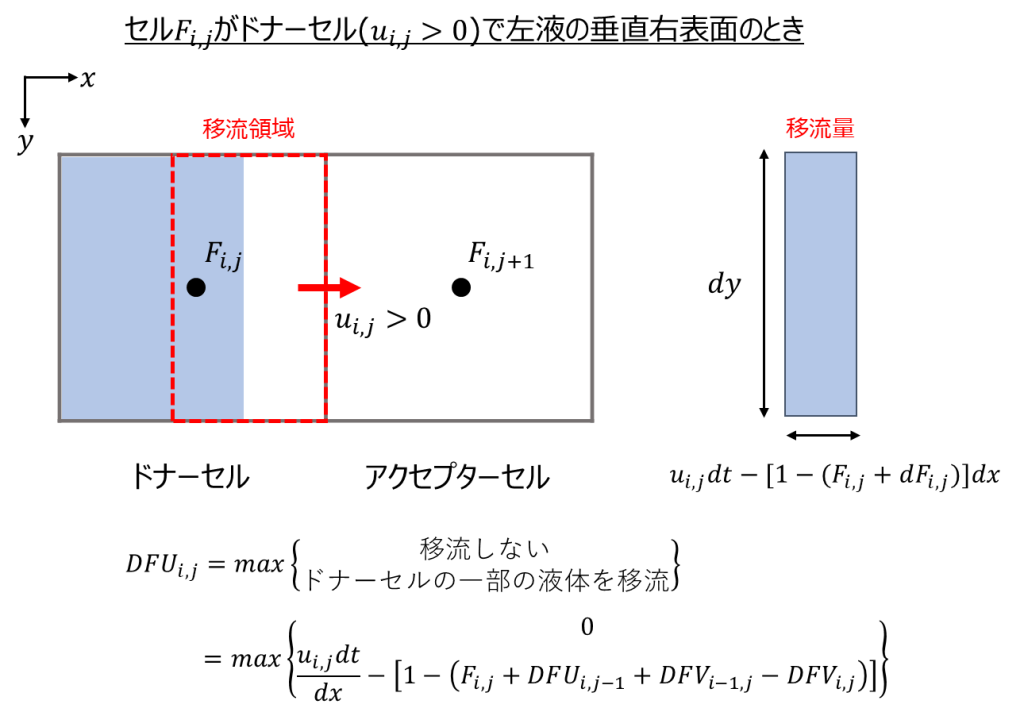
\(F_{i.j}\)のセルがドナーセルで左液の右垂直表面の場合、少し状況が複雑で\(x\)方向への移流量\(DFU_{i,j}\)は以下のように2パターン考えらえれます。
流速が小さく移流領域が液体が存在する領域に到達していない場合、その移流量は\(0\)となります。(空気が輸送された状態で液体はセル内にとどまる。)
一方、到達した場合は以下のような式で表されます。
&(移流領域内の液体存在面積):(移流量)=(セル内の液体存在面積):(液体体積率)\\
&\Leftrightarrow
u_{i,j}dtdy-[1-(F_{i,j}+dF_{i,j})]dxdy:DFU_{i,j}=F_{i,j}dxdy:F_{i,j}\\
&\Leftrightarrow
DFU_{i,j}=\frac{F_{i,j}u_{i,j}dt}{dx}-[1-(F_{i,j}+dF_{i,j})]\\
&\Leftrightarrow
DFU_{i,j}=\frac{F_{i,j}u_{i,j}dt}{dx}-[1-(F_{i,j}+DFU_{i,j-1}+DFV_{i,-1,j}-DFV_{i,j})]\\
\tag{8}
\end{align}
移流量としては上記のうち、より大きいほうを採用すればよいので、まとめると以下のように書けます。
DFU_{i,j}=max\left\{
\begin{array}{c}
0 \\
\frac{F_{i,j}u_{i,j}dt}{dx}-[1-(F_{i,j}+DFU_{i,j-1}+DFV_{i-1,j}-DFV_{i,j})]
\end{array}
\right\}\\
\tag{8}
\end{align}
上記は一例ですが、このような場合分けを様々なパターンで繰り返し、\(u,v\)方向の移流量\(DFU,DFV\)を計算していきます。
以下に今回行った場合分けの全パターン一覧を記載します。\(v\)方向の場合分けなどは少々複雑で、液体の消失が生じないように巧妙にルール分けされています。この辺はまたいつか別記事で述べられればと思います。

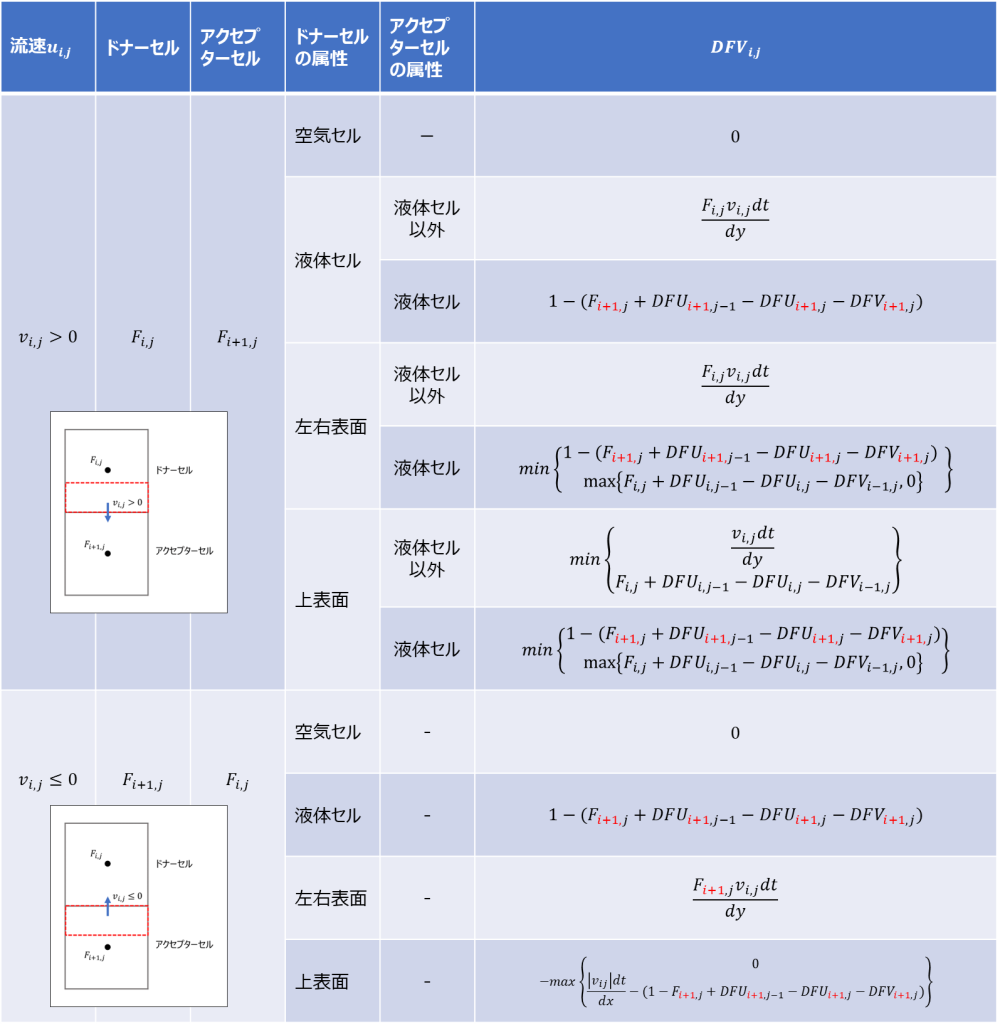
上記の\(DFU,DFV\)が求まったならば、式\((6)\)に基づい\(F\)を更新します。以上がVOF値の移流処理になります。
VOF値の補正:DFVの補正
今回、液体がオーバーハングするような状況は考えないものとするので、液体中の気泡や気体中の液体は上表面に集める補正処理を施します。
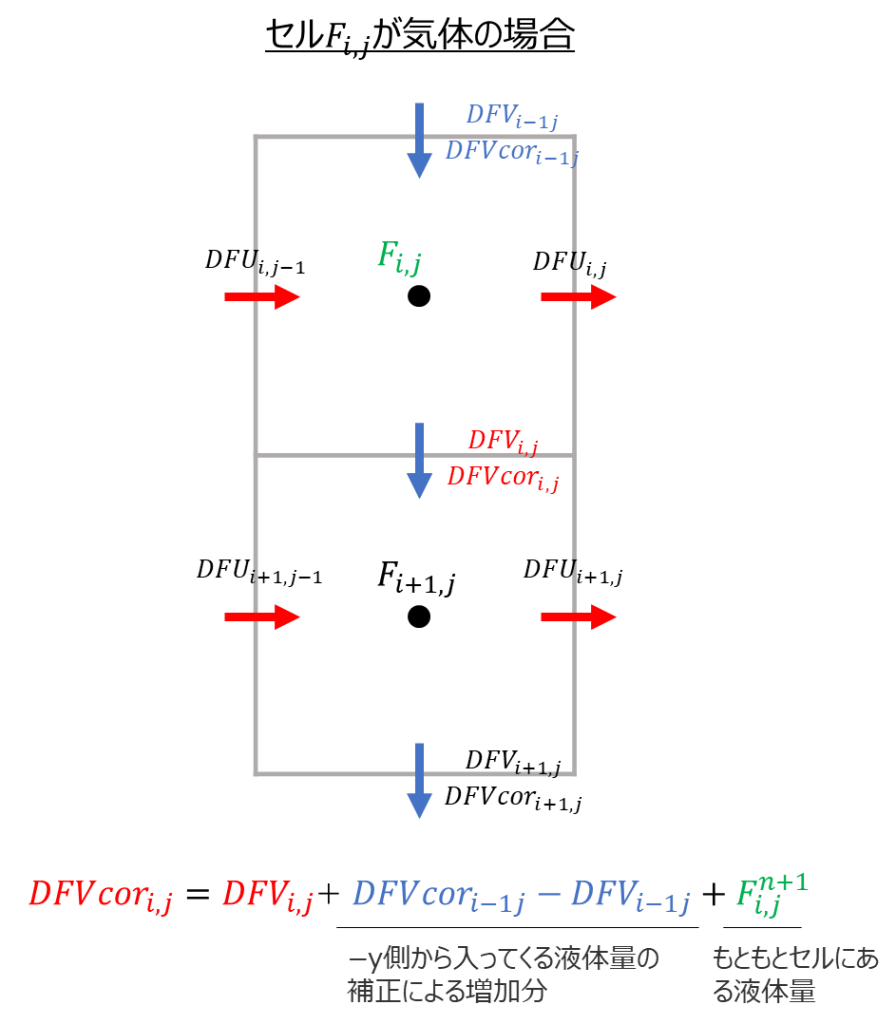
例えば\({NF}_{i.j}\)が閾値判定で気体セルと認識されたとしても、\(F_{i,j}\)がわずかに値を有する場合があります。気体判定のセルの移流量は0になるので、このようなわずかな液体でも無視して計算を進めてしまうと、徐々に液体が消失してしまう現象につながります。そこで\(DFV\)の補正量\(DFVcor\)を以下のように求めます。
&{DFVcor}_{i,j}=DFV_{i,j}+\Delta DFV_{i,j}\\
&\Leftrightarrow
{DFVcor}_{i,j}=DFV_{i,j}+(-y側から入ってくる液体量の補正による増加量)+(もともとセルにある液体量)\\
&\Leftrightarrow
{DFVcor}_{i,j}=DFV_{i,j}+{DFVcor}_{i-1,j}-DFV_{i-1,j}+F^{n+1}_{i,j}\tag{9}
\end{align}
上記のような補正により気体中のわずかな液体はその下の要素に運び込まれることとなります。
また下の要素\(F_{i+1,j}\)が液体の場合、\({DFVcor}_{i,j}\)は以下のように求めます。
&{DFVcor}_{i,j}=DFV_{i,j}+\Delta DFV_{i,j}\\
&\Leftrightarrow
{DFVcor}_{i,j}=DFV_{i,j}+(下のセルの+y側から出ていく液体量の補正による増加分)+(下のセルにもともとある気体量)\\
&\Leftrightarrow
{DFVcor}_{i,j}=DFV_{i,j}+{DFVcor}_{i+1,j}-DFV_{i+1,j}+1-F^{n+1}_{i+1,j}\tag{10}
\end{align}
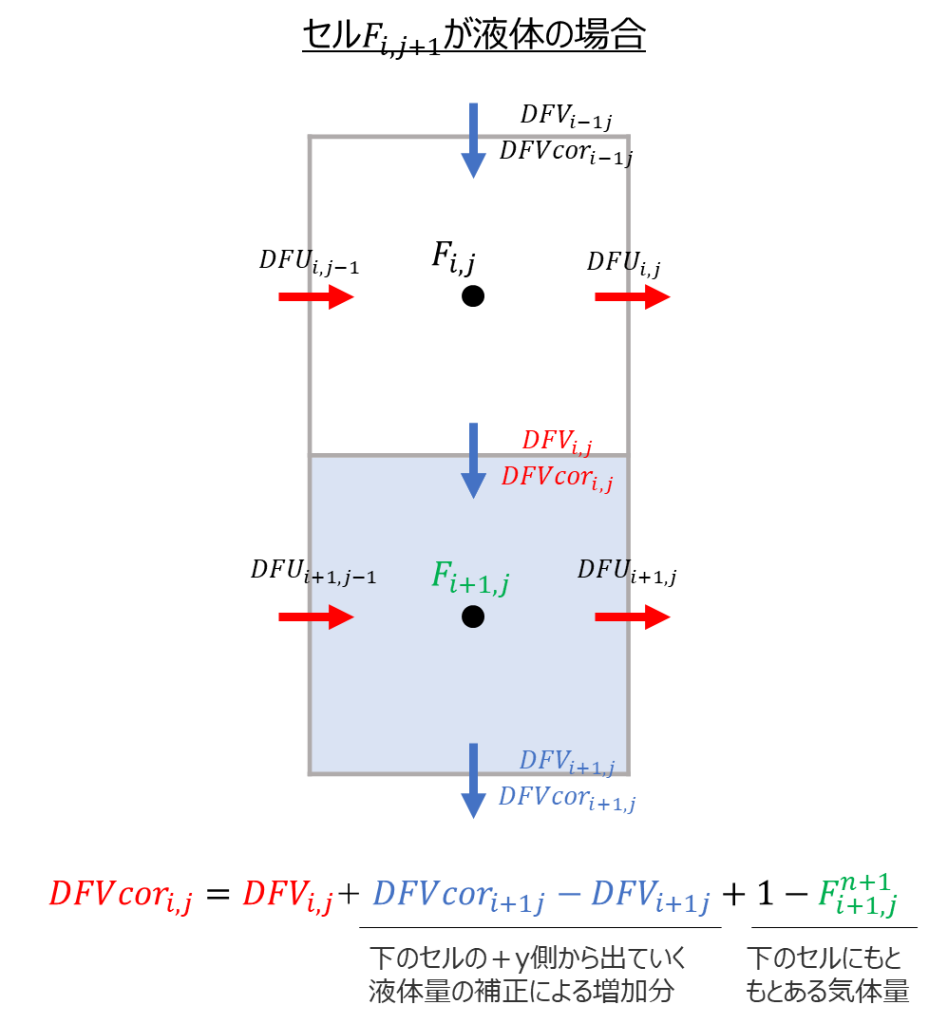
上記のような補正により液体中のわずかな空気\((1-F^{n+1}_{i,j})\)を上表面に移動することが出来ます。
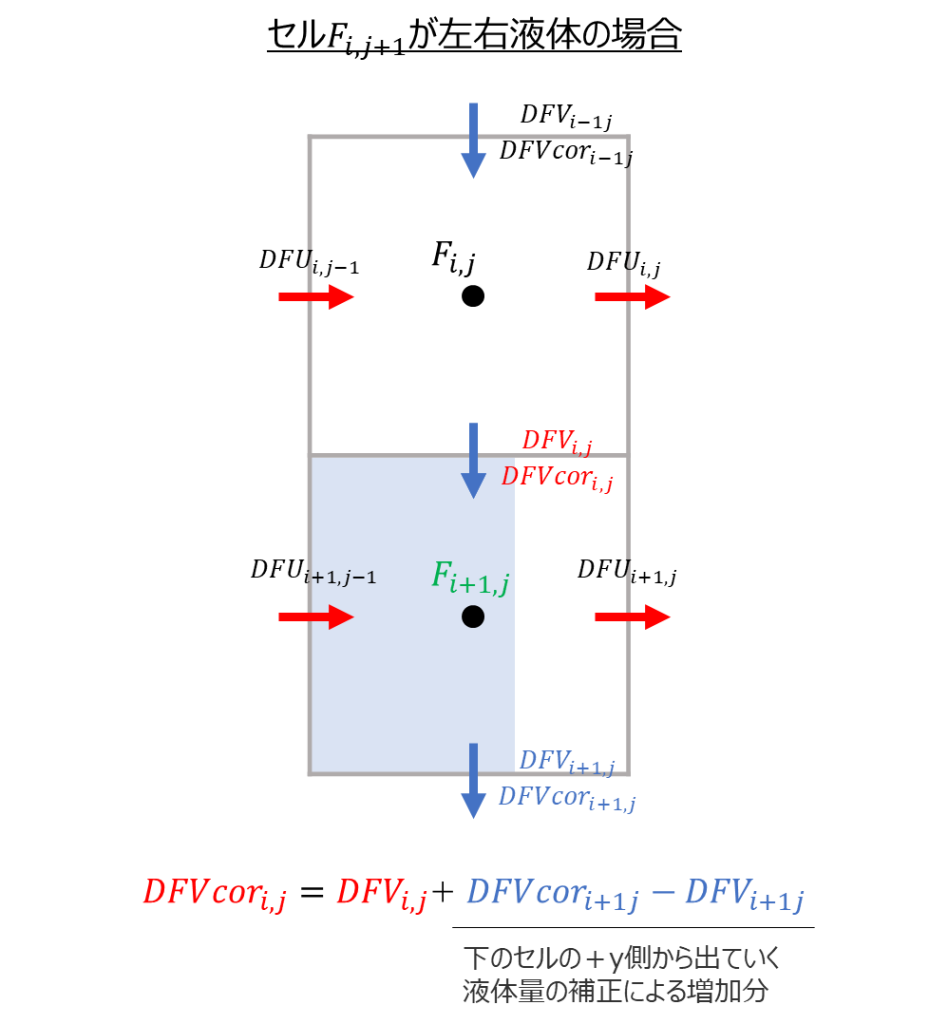
最後は\(F_{i+1,j}\)が界面セルの場合です。この場合は下のセルの\(+y\)側から出ていく液体量の補正による増加分のみ考え、もともとある液体量(気体量)は保つようにします。
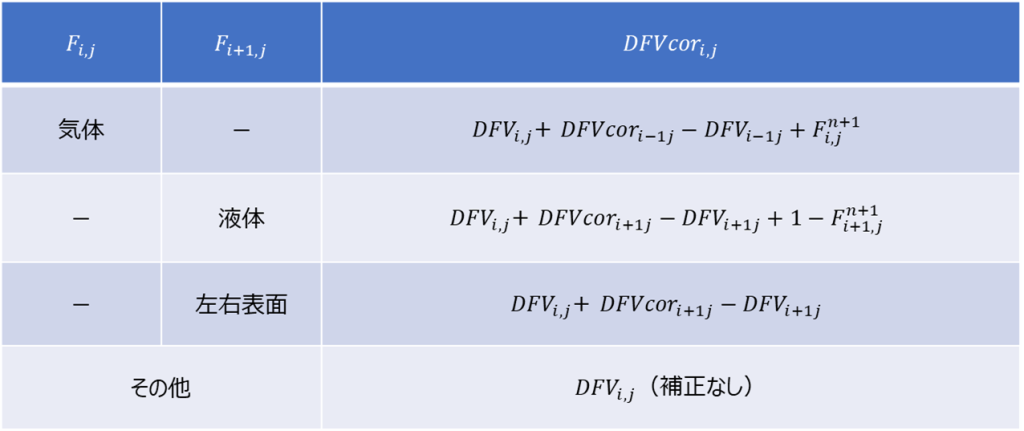
以下にここまでの補正処理の一覧をまとめておきます。
補正された\(Fcor\)は求めた\(DFVcor\)を用いて以下のように求められます。
Fcor_{i.j}^{n+1}=F_{i.j}^{n}-\left( DFU_{i,j}- DFU_{i,j-1}+{DFVcor}_{i,j}-{DFVcor}_{i-1,j}\right)
\tag{11}
\end{align}
\(F_{i.j}^{n+1}\)ではなく\(F_{i.j}^{n}\)に対して補正をかけに行くことに注意しましょう。以上のような操作で液体中の気泡、気体中の液体を上表面に集めることができます。
速度の補正
最後にここまでの補正により決定された各セルの属性情報\(NF\)に基づき、前回の方法と同様に流速\(u,v\)の境界条件を更新して終了です。以上がVOF法の主要部分に関する一通りの説明になります。
MATLABコード
こちらにここまでの内容をMATLABにて実装したコードをアップロードしました。境界条件部分など記事中では説明しきれていない細かい部分が気になる方はこちらのコードを参照してください。以下にセル数30*30で計算した結果の一例を示します。なんとなく雰囲気は出ているのではないでしょうか。
体積の保存性は以下の通りです。以下図は初期の液体量を100%としたときの時間変化を示しています。時間がたっても液体が消失するようなことはなさそうです。
おわりに
今回はVOF法について解説し、簡易版の実装まで行いました。単純に基礎方程式を解くだけでなく、適切な後処理を施すことで界面をうまく表現する必要がある点がVOF法の難しい所だと思いました。界面状況に応じたパターン分けはほんとしんどい…。
今回は界面のオーバーハングや表面張力などの効果は省略しましたが、エッセンスはつかむことが出来たので、この辺のアップデートはまた別の機会にチャレンジしたいと思います。VOFはしばらくはお腹一杯だ…。
参考文献
[1] 米山望, 守屋祥一 (1995): VOF法を用いた自由液面の数値解析手法, 水工学論文集, 第39巻, 373-378.
[2] 米山望, 角湯正剛 (1996): 自由液面解析コード(FRESH)の開発-3次元化と並列化-, 電力中央研究所報告 U95063.
[3] 富村寿夫 (2022): エクセルでできる熱流体のシミュレーション
[4] 米山望(1998): 自由液面解析コード(FRESH)の開発,2.コードの概要, b.VOF法, 日本流体力学会ウェブサイト「ながれマルチメディア」 https://www2.nagare.or.jp/mm/98/yoneyama/japanese/gaiyoub.htm



コメント