はじめに
今回も前回に引き続きコロケート格子におけるキャビティフローの計算方法の解説を進めていきます。前回は基礎方程式の離散化を一通り行いました。今回は境界条件の説明から始めて、実装したプログラムをベンチマークと比較評価するところまで行います。
境界条件① コロケート格子上の境界条件の与え方
境界条件はセル界面に課す方法とセル中心に課す方法があります。今回は計算領域を最外周のセル中心までとし、境界条件はセル中心に直接課す方針とします。例として7*7のセルで図示すると各変数の配置は以下のようになります。

ここで\(x\)方向を下向きにとった座標系としています。これは配列の行を\(x\)方向、列を\(y\)方向と紐づけて考えるためであり実装上の都合です。添え字は実装時の配列番号を表します。
境界条件② キャビティ流れの境界条件
キャビティ流れの境界条件は以下の図2のように与えます。
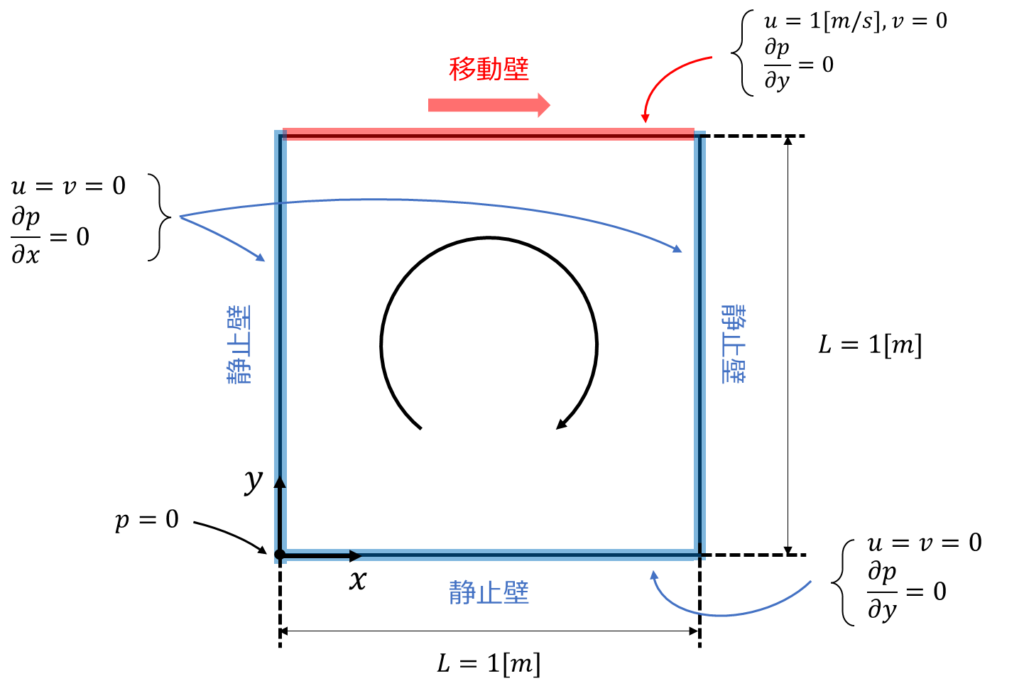
流速の境界条件に関しては、\(+y\)側を移動壁\(u=1, v=0\)として、それ以外の壁を静止壁\(u=v=0\)として与えます。いわゆる滑りなし条件です。
一方、圧力の境界条件はどのように与えるべきでしょうか?圧力の境界条件は好き勝手に決めて良いというわけではなく上記の流速の境界条件に基づいて決める必要があります。圧力と流速の関係はナビエ・ストークス方程式で規定されるのでした。そこで静止壁上(\(-y\)側)のナビエ・ストークス方程式を考えてみます。2次元のナビエ・ストークス方程式は以下のように書けました。
\frac{\partial }{\partial t}
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
+
\left[
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
\right]
\left(
\begin{array}{c}
u \\
v
\end{array}
\right)
=-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
p
+
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial x^2} + \frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial x^2} +\frac{\partial ^2 }{\partial y^2}
\end{array}
\right)
\left(
\begin{array}{c}
u \\
v
\end{array}
\right) \\\\
\tag{1}
\end{align}
静止壁では時間にかかわらず\(u=v=0\)なので、圧力と流速の間には以下のような関係が成り立ちます。
&0
=-\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
p
+
ν
\left(
\begin{array}{c}
\frac{\partial ^2 }{\partial y^2}\\
\frac{\partial ^2 }{\partial y^2}
\end{array}
\right)
\left(
\begin{array}{c}
u \\
v
\end{array}
\right) \\\\
&→
\frac{1}{ρ}
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
p
=
ν
\left(
\begin{array}{c}
\frac{\partial ^2 u}{\partial y^2}\\
\frac{\partial ^2 v}{\partial y^2}
\end{array}
\right)
\tag{2}
\end{align}
この式は「境界における圧力は流速勾配によって変動している」ことを示しています。壁面上の流速は常に\(u=v=0\)で固定されているにもかかわらず、圧力は変動する点は興味深いです。
ここで仮に\(y=0\)の静止壁での圧力境界値を決めたいならば、上式の第2成分を離散化して解くこととなります。(第1成分を解くことで、\(y=0\)における\(x\)方向の圧力勾配を規定することが出来きますが、\(y=0\)における圧力値はそもそも分からないのだから、これを解いても静止壁上の圧力は決まりません。対して、第二成分は\(y\)方向の圧力勾配を規定するので、計算領域内の圧力から静止壁上の圧力を規定できます。)
ただし式\((2)\)から境界の圧力を決めるのは少々厄介で、右辺の流速の二階微分を境界上でどのように処理するかが問題です。厳密には境界外に仮想セルを設置して速度の二階微分を計算する、など行われるようですが少々煩雑なのでここでは以下のように考えて簡略化して考えます。
式\((2)\)を無次元化すると以下のようになります。
\left(
\begin{array}{c}
\frac{\partial }{\partial \tilde{x}} \\
\frac{\partial }{\partial \tilde{y}}
\end{array}
\right)
\tilde{p}
=
\frac{1}{\rm{Re}}
\left(
\begin{array}{c}
\frac{\partial ^2 \tilde{u}}{\partial \tilde{y}^2}\\
\frac{\partial ^2 \tilde{v}}{\partial \tilde{y}^2}
\end{array}
\right)
\tag{3}
\end{align}
ここで\(\rm{Re}\)が十分大きく、壁面での圧力の法線方向の勾配は小さくなると仮定し、以下が成り立つものと仮定します。(ただしこれが本当に成り立つのかは疑問の余地があります。仮にレイノルズ数が十分大きかったとしても一般的には壁面近傍における流速勾配も大きいため右辺を無視出来るとは限りません。このため計算都合の簡略化と思われます。)
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
p
=
0\tag{4}
\end{align}
上式が図2にも示した壁面における圧力の境界条件です。このように設定することで厳密性は失いますが右辺の二階微分の離散化を考える必要がなくなります。このような恣意的な操作を行って計算が破綻なくできるのか心配になりますが、やってみると計算自体はできてしまうのが不思議です。
また、smac法において実際に圧力の境界条件が必要となるポアソン方程式(以下式)は、圧力そのものではなく、圧力補正量\(\delta p\)に関する方程式でした。
\left(
\frac{\partial ^2 }{\partial x^2}+\frac{\partial^2 }{\partial y^2}
\right)
\delta p
=
\frac{ρD^{*}}{\Delta t}
\tag{5}
\end{align}
p^{n+1}
=
p^{n}+\delta p\tag{6}
\end{align}
従って、実際にプログラムの中で用いられる境界条件は式\((4)\)を圧力補正量\(\delta p\)に書き換えた以下の式となります。
\left(
\begin{array}{c}
\frac{\partial }{\partial x} \\
\frac{\partial }{\partial y}
\end{array}
\right)
\delta p
=
0\tag{7}
\end{align}
この式変形は唐突に思えるかもしれませんか、圧力\(p\)に関して式\((4)\)はいかなる時刻でも成り立っている必要があるので、式\((6)\)から考えても、式\((7)\)が成り立つのは自然なことです。
またナビエ・ストークス方程式\((1)\)では圧力は勾配の形で含まれており、問題となるのは圧力の空間的な差分のみとなります。したがってその基準値はどのようにとってもよいです。(例えば圧力を\(p=p_0(基準圧)+p^{\prime}(変動圧)\)に分解して式\((1)\)に代入すると空間微分で基準圧は消えてしまうことが分かる。)
特に今回は閉空間の流れであり、境界条件は圧力を勾配(ノイマン条件)でしか規定していません。ポアソン方程式を行列形式に書き下すとわかりますが、これは係数行列がランク落ちとなっており、解が一意に定まらない状況に相当します。イメージ的にはノイマン条件が境界条件を領域内部から決めようとするのに対し、領域内部は境界条件から決めようとするので条件が定まらないといった感じです。(1次元系で考えてみるとわかりやすい)
今回のように反復法で解く場合、ランク落ちでも代入を繰り返すアルゴリズムが破綻するわけではないので、何らかの解を得ること自体はできてしまいます。しかしながら、ランク落ち状態で計算を続けると、解が不安定になり収束が遅くなることが知られています。(以前試した際は、発散こそしなかったが圧力がマイナス方向に不自然にどんどん大きくなったりした。)こういった理由からキャビティ流れでは、どこかしら1点で圧力を固定するのが一般的です。今回は原点位置で\(p=0[\rm{kPa}]\)と固定することとします。
これらの圧力の境界条件はSOR法の反復の中で、各反復のたびに毎回規定することで、境界条件を満たす圧力場を得ることが出来きます。
MATLABコード
ここまでの内容を踏まえて作成したソースコードを以下に記載します。(こちらにもアップしています。 )
% 初期化
clear all;
% グローバル変数宣言
global x y dt nx ny ite_max dLx dLy Lx Ly rho nu
% パラメーター
Lx = 1;% 計算領域
Ly = 1;% 計算領域
nx = 40;% 要素数
ny = 40;% 要素数
dLx = Lx / nx;% 要素サイズ
dLy = Ly / ny;% 要素サイズ
nu = 1;% 動粘性係数
rho = 1;% 密度
t_max = 100;% SIM計算時間
dt = 0.0001;% タイムステップ
ite_max = t_max / dt;% 反復数
% 座標の生成
x = 0 : Lx / nx : Lx;
y = Ly : - Ly / ny : 0;
[X, Y] = meshgrid(x, y);
% 配列確保
u = zeros(nx, ny);% セル中心での速度
v = zeros(nx, ny);% セル中心での速度
p = zeros(nx, ny);% セル中心での圧力
dp = zeros(nx, ny);% セル中心での補正圧力
diffx = zeros(nx, ny);
diffy = zeros(nx, ny);
advx = zeros(nx, ny);
advy = zeros(nx, ny);
usb = zeros(nx - 1, ny - 2);% セル界面での中間速度
vsb = zeros(nx - 2, ny - 1);% セル界面での中間速度
% 境界条件
bc.ue = 0;% 東側
bc.us = 0;% 南側
bc.uw = 0;% 西側
bc.un = 1;% 北側
bc.ve = 0;% 東側
bc.vs = 0;% 南側
bc.vw = 0;% 西側
bc.vn = 0;% 北側
% 境界条件の設定
[u, v] = setBC(u, v, bc);
% 時間発展
for ite = 2 : ite_max
% 拡散項の計算
[diffx, diffy] = diffusion(u, v, diffx, diffy);
% 移流項の計算
[advx, advy] = advection(u, v, advx, advy);
% 移流拡散による時間進行を計算
u = u + (nu * diffx + advx) * dt;
v = v + (nu * diffy + advy) * dt;
% セル界面での中間速度を計算
[usb, vsb] = midvel(usb, vsb, u, v, p);
% 補正圧力の計算
[dp, ds] = poisson(usb, vsb, dp);
% 次ステップ圧力の計算
p = p + dp;
% 次ステップ流速の計算
[u, v] = velupdate(u, v, p);
% 境界条件の設定
[u, v] = setBC(u, v, bc);
% コマンドウィンドウへの出力
txt = ['ite = ', num2str(ite), ' / ', num2str(ite_max)];
disp(txt);
% リアルタイム可視化
vis_contour('u', ite, u, -0.8, 0.8, 1);
vis_contour('v', ite, v, -0.5, 0.5, 2);
vis_vector('vec', ite, u, v, 3)
%vis_contour('p', ite, p, -3, 3, 4);
%vis_contour('ds', ite, ds, -0.01, 0.01, 5);
end
%% 以下関数
function[u, v] = setBC(u, v, bc)
% グローバル変数呼び出し
global nx ny
u(nx, :) = bc.ue;
u(:, 1) = bc.us;
u(1, :) = bc.uw;
u(:, ny) = bc.un;
v(nx, :) = bc.ve;
v(:, 1) = bc.vs;
v(1, :) = bc.vw;
v(:, ny) = bc.vn;
end
function[diffx, diffy] = diffusion(u, v, diffx, diffy)
% グローバル変数呼び出し
global nx ny dLx dLy
for i = 2 : nx - 1
for j = 2 : ny - 1
diffx(i, j) = (u(i + 1, j) - 2 * u(i, j) + u(i - 1, j))/(dLx)^2 + (u(i , j + 1) - 2 * u(i, j) + u(i, j - 1))/(dLy)^2 ;
diffy(i, j) = (v(i + 1, j) - 2 * v(i, j) + v(i - 1, j))/(dLx)^2 + (v(i , j + 1) - 2 * v(i, j) + v(i, j - 1))/(dLy)^2 ;
end
end
end
function[advx, advy] = advection(u, v, advx, advy)
% グローバル変数呼び出し
global nx ny dLx dLy
for i = 2 : nx - 1
for j = 2 : ny - 1
advx(i, j) = -(u(i, j) * (u(i + 1, j) - u(i - 1, j)) / (2 * dLx) + abs(u(i, j)) * (2 * u(i, j) -u(i - 1, j) - u(i + 1, j)) / (2 * dLx) ...
+ v(i, j) * (u(i, j + 1) - u(i, j - 1)) / (2 * dLy) + abs(v(i, j)) * (2 * u(i, j) -u(i , j - 1) - u(i, j + 1)) / (2 * dLy));
advy(i, j) = -(u(i, j) * (v(i + 1, j) - v(i - 1, j)) / (2 * dLx) + abs(u(i, j)) * (2 * v(i, j) -v(i - 1, j) - v(i + 1, j)) / (2 * dLx) ...
+ v(i, j) * (v(i, j + 1) - v(i, j - 1)) / (2 * dLy) + abs(v(i, j)) * (2 * v(i, j) -v(i , j - 1) -v(i, j + 1)) / (2 * dLy));
end
end
end
function[usb, vsb] = midvel(usb, vsb, u, v, p)
% グローバル変数呼び出し
global nx ny dLx dLy dt rho
for i = 1 : nx - 1
for j = 1 : ny - 2
usb(i, j) = (u(i + 1, j + 1) + u(i, j + 1)) / 2 - (dt / rho) * (p(i + 1, j + 1) - p(i, j + 1)) / dLx;
end
end
for i = 1 : nx - 2
for j = 1 : ny -1
vsb(i, j) = (v(i + 1, j + 1) + v(i + 1, j )) / 2 - (dt / rho) * (p(i + 1, j + 1) - p(i + 1, j )) / dLy;
end
end
end
function[dp, ds] = poisson(usb, vsb, dp)
% グローバル変数呼び出し
global nx ny dLx dLy dt rho
% ポアソン方程式の係数定義
ac = zeros(nx, ny);
an = zeros(nx, ny);
ae = zeros(nx, ny);
as = zeros(nx, ny);
aw = zeros(nx, ny);
ac(:, :) = 2 * ((1/(dLx)^2) +(1/(dLy)^2));
an(:, :) = 1 / (dLy)^2;
ae(:, :) = 1 / (dLx)^2;
as(:, :) = 1 / (dLy)^2;
aw(:, :) = 1 / (dLx)^2;
% SOR法
ds = zeros(nx, ny);
eps = 10^(- 5);
ite_pmax = nx * ny * 20;% 反復回数
alpha = 1.7;% 緩和係数
for ite_p = 1 : ite_pmax% SOR法により圧力補正値を求める。
error = 0;
for i = 1 : nx
for j = 1 : ny
if i == 2 && j == 2% 圧力の基準点を固定しておく。
dp(i, j) = 0;
elseif i == 1% 西側境界条件
dp(i, j) = dp(i + 1, j);
elseif i == nx% 東側境界条件
dp(i, j) = dp(nx - 1, j);
elseif j == 1% 南側境界条件
dp(i, j) = dp(i, j + 1);
elseif j == ny% 北側境界条件
dp(i, j) = dp(i, ny - 1);
else% 内部領域
ds(i, j) = (usb(i, j - 1) - usb(i - 1, j - 1))/dLx + (vsb(i - 1, j) - vsb(i - 1, j - 1))/dLy;
dp_new= ( 1 / ac(i, j) ) * ...
( ae(i, j) * dp(i + 1, j) + aw(i, j) * dp(i - 1, j) + an(i, j)* dp(i, j + 1) + as(i, j)* dp(i, j - 1) - (rho / dt) * ds(i, j) );
error = max(abs(dp_new - dp(i, j)), error);
dp(i, j) = dp(i, j) + alpha * (dp_new - dp(i, j));
end
end
end
if error < eps % 収束条件が満たされたらループを抜ける。
break
end
if ite_p >= ite_pmax
disp('最大反復回数に達しました。収束条件を満たしていません。');
end
end
end
function[u, v]= velupdate(u, v, p)
% グローバル変数呼び出し
global nx ny dLx dLy dt rho
for i = 2 : nx - 1
for j = 2 : ny - 1
% セル中心速度には圧力は加えてなかったので、更新した圧力を加算する。(界面補間速度には更新前の圧力を加えていた。)
u(i, j) = u(i, j) -(dt / rho) * ((p(i + 1, j) - p(i - 1, j))/(2 * dLx));
v(i, j) = v(i, j) -(dt / rho) * ((p(i, j + 1) - p(i, j - 1))/(2 * dLy));
end
end
end
function[] = vis_contour(filename, timestep, u, maxrange, minrange, fignum)
% グローバル変数呼び出し
global nx ny dt x y Lx Ly nu rho
figure(fignum);
h = imagesc(x, y, flip(u));
xlabel('y')
ylabel('x')
view(270, 90); % 視点の設定
xticks(0 : round(Lx / 5, 1) : Lx);
yticks(0 : round(Ly / 5, 1) : Ly);
h.AlphaData = isfinite(u); % NaNやInfを透明にする
title(filename);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 16);
axis equal;
axis tight;
axis on;
colorbar;
caxis([maxrange minrange])
% コメント
str_1 =['time = ', num2str(timestep * dt, '%.4f')];
str_2 =['Re = ', num2str(1 / nu, '%.f')];
str_3 =['rho = ', num2str(rho, '%.1f'),', nu = ', num2str(nu, '%.3f')];
str_4 =['nx = ', num2str(nx, '%.0f'),', ny = ', num2str(ny, '%.0f')];
str = {str_1, str_2, str_3, str_4};
text(0.1, 0.01, str)
% pngで保存
folder = [filename, '_re', num2str(1/nu),'_dt', num2str(dt),'_nx', num2str(nx),'_ny', num2str(ny)];
if timestep == 2
mkdir(folder);
filename2 = [folder, '/', filename, '_', num2str(timestep), '.png'];
saveas(gcf, filename2)
elseif rem(timestep, 10) == 0
filename2 = [folder, '/', filename, '_', num2str(timestep), '.png'];
saveas(gcf, filename2)
end
end
function[] = vis_vector(filename, timestep, u, v, fignum)
% グローバル変数呼び出し
global dt nu nx ny
figure(fignum);
h = quiver(flipud(rot90(u)),flipud(rot90(v))) ;
h.Color = 'r';
h.AutoScaleFactor= 6;
title(['time = ', num2str(timestep * dt, '%.4f'),', Re = ', num2str(1 / nu, '%.f')]);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 16);
axis equal; axis tight; axis on;
xlim([1 nx]);
ylim([1 ny]);
% pngで保存
folder = [filename, '_re', num2str(1/nu),'_dt', num2str(dt),'_nx', num2str(nx),'_ny', num2str(ny)];
if timestep == 2
mkdir(folder);
filename2 = [folder, '/', filename, '_', num2str(timestep), '.png'];
saveas(gcf, filename2)
elseif rem(timestep, 10) == 0
filename2 = [folder, '/', filename, '_', num2str(timestep), '.png'];
saveas(gcf, filename2)
end
end
計算結果
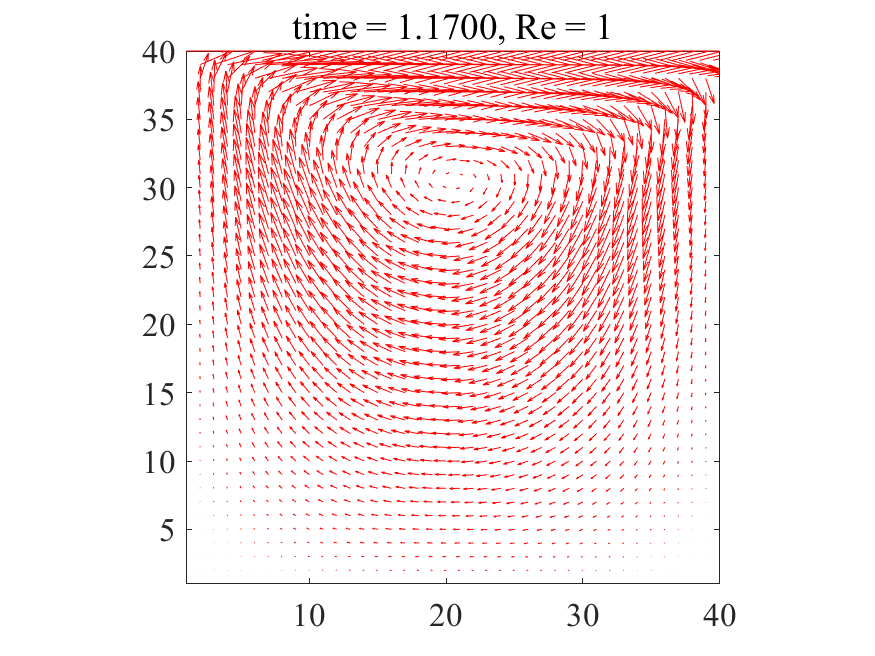
上記のコードにおいて、密度\(\rho = 1\)に設定すれば、レイノズル数\(\rm{Re}\)は動粘性係数\(\nu\)の逆数として与えることが出来ます。以下に\(\rm{Re}=500\)の場合の解析結果を記載します。
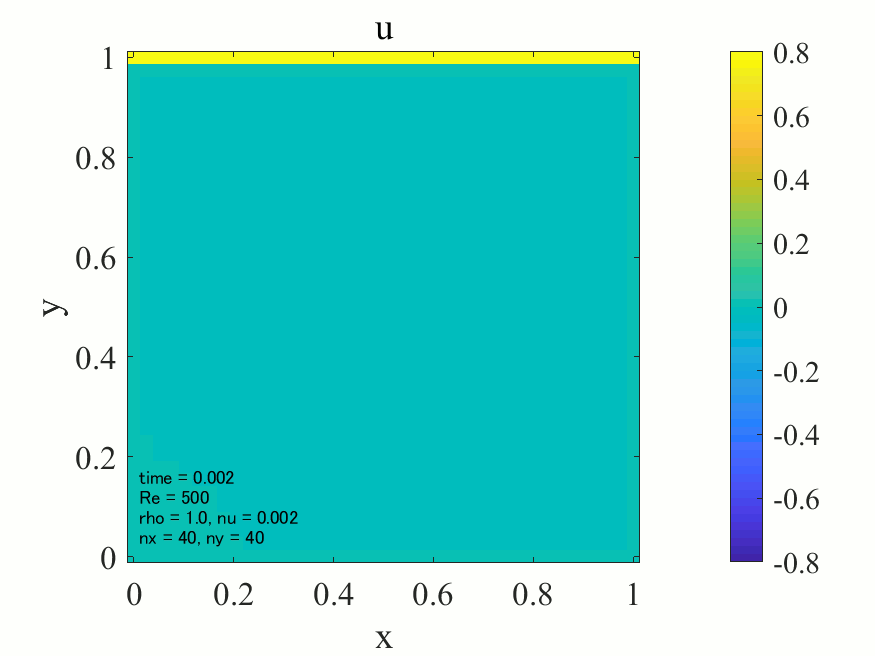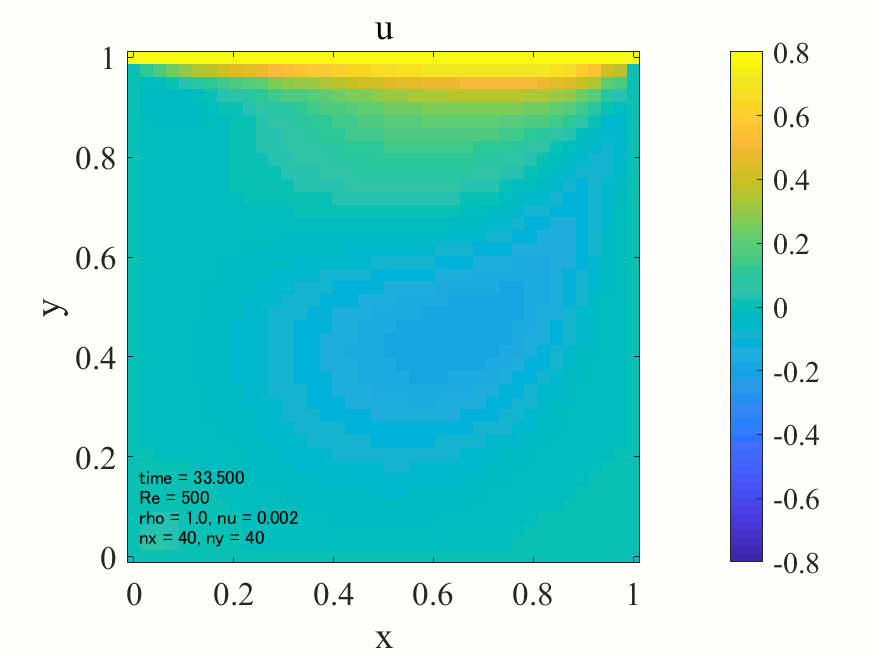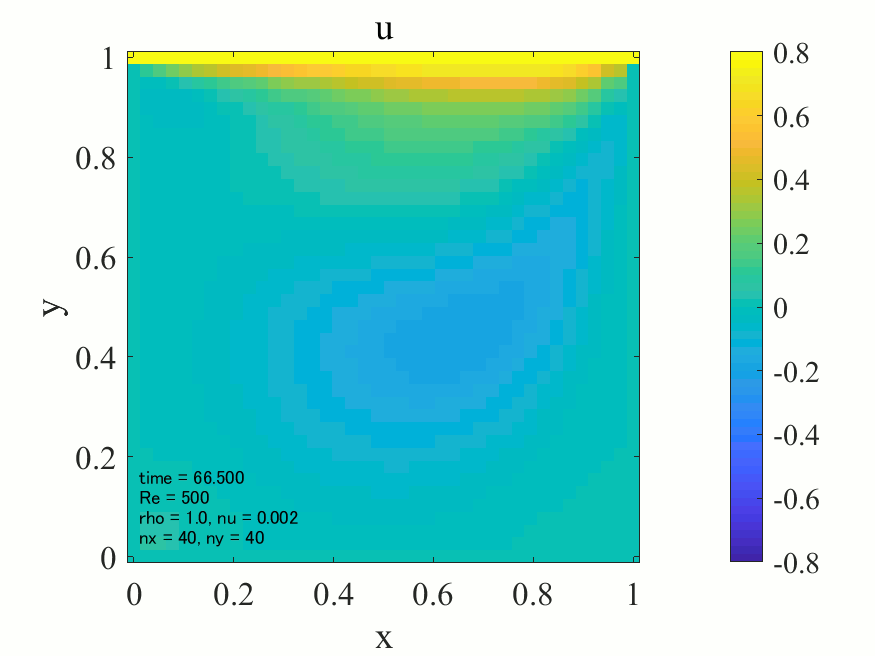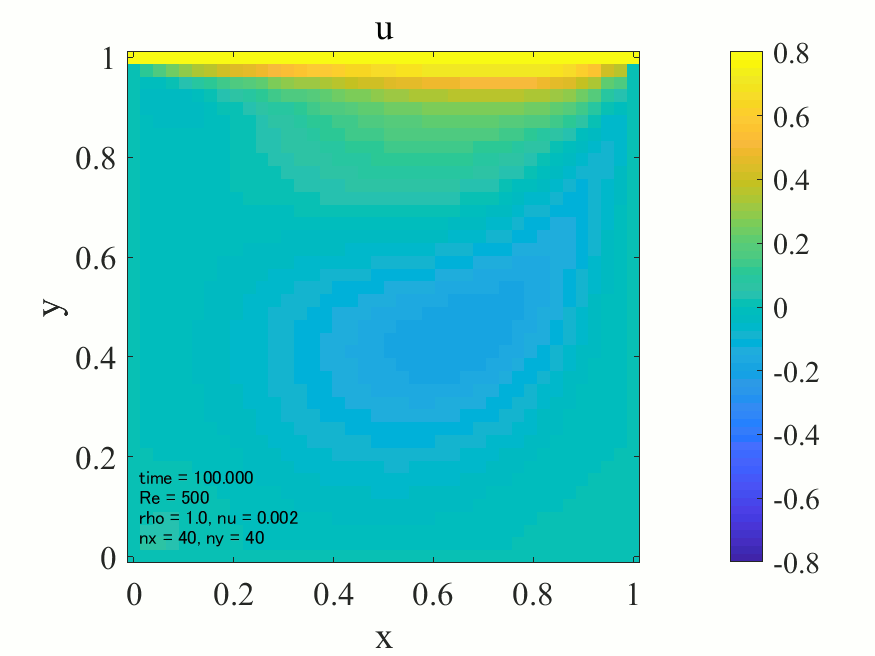
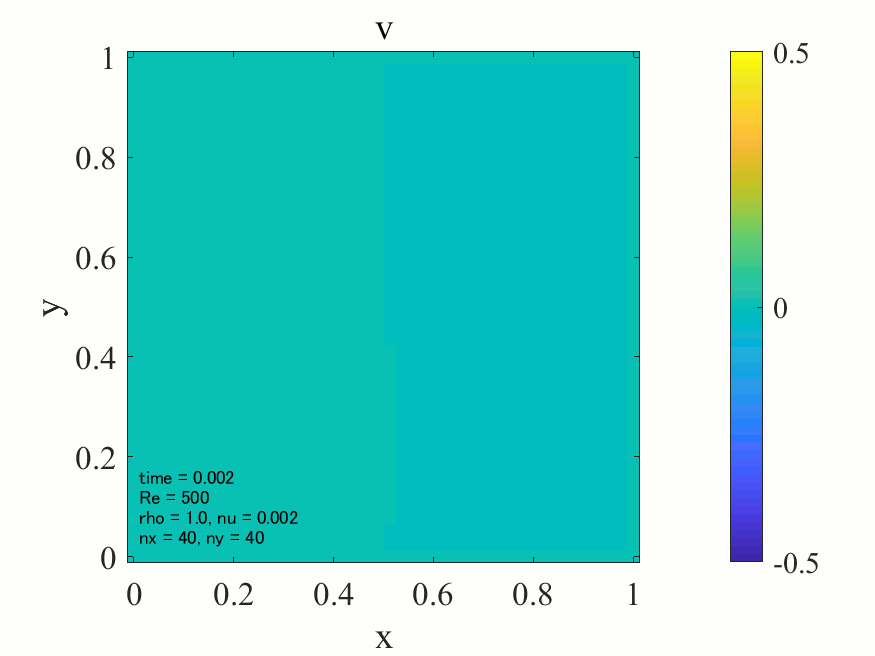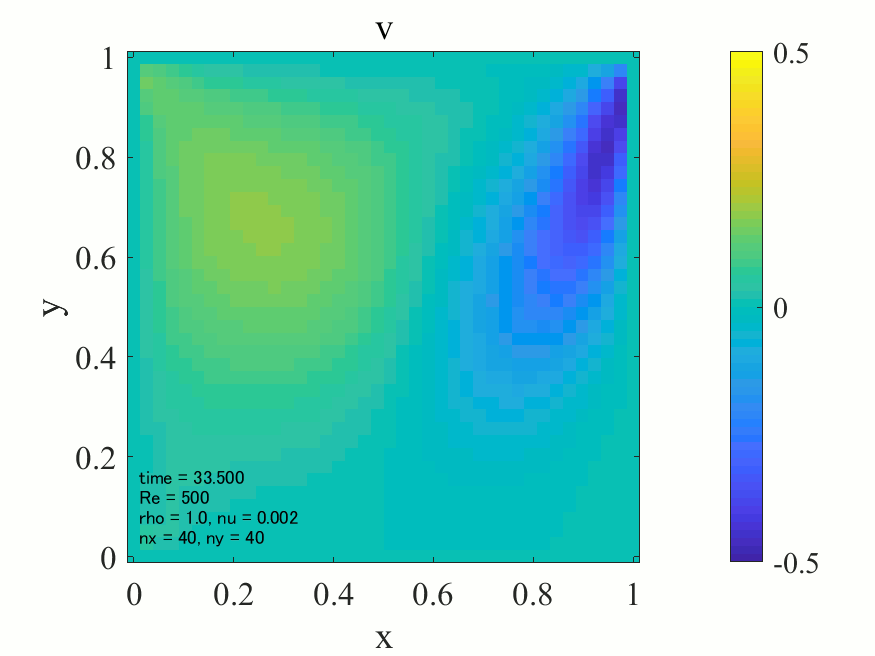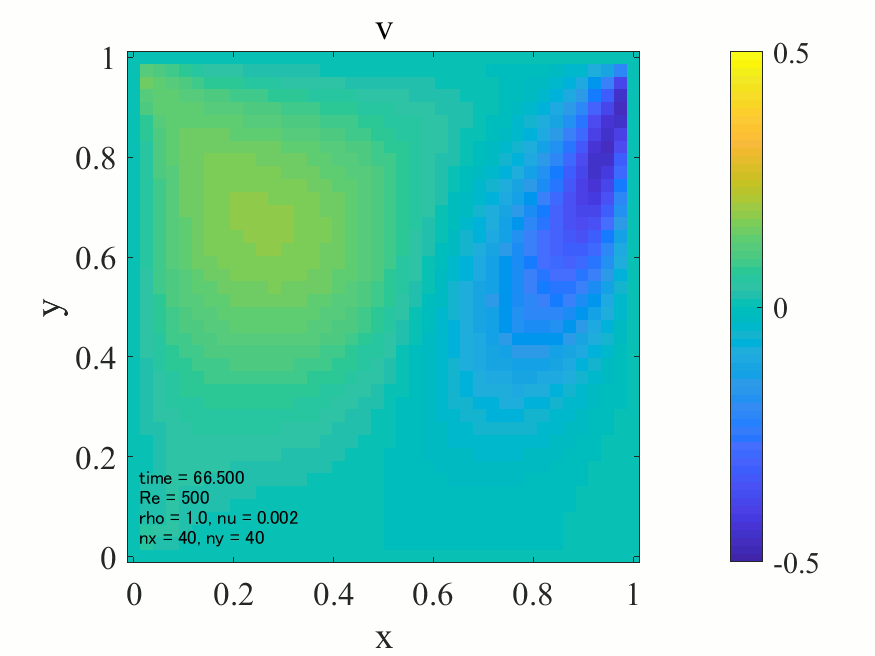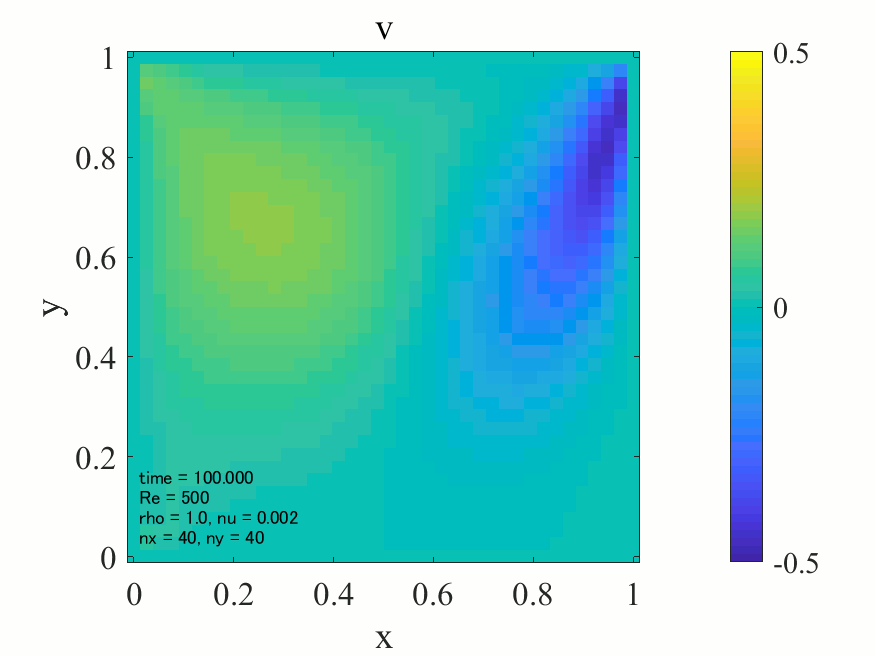
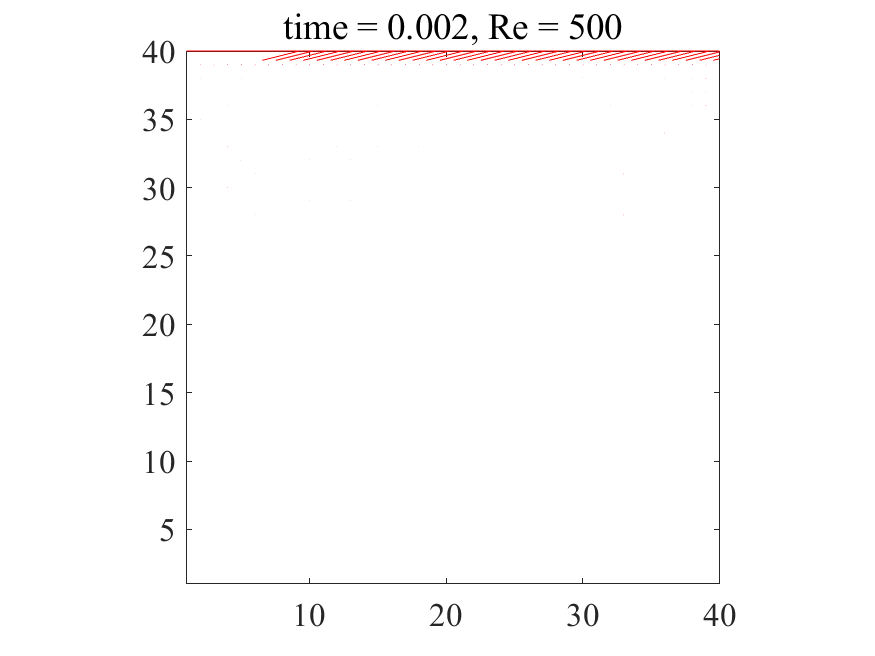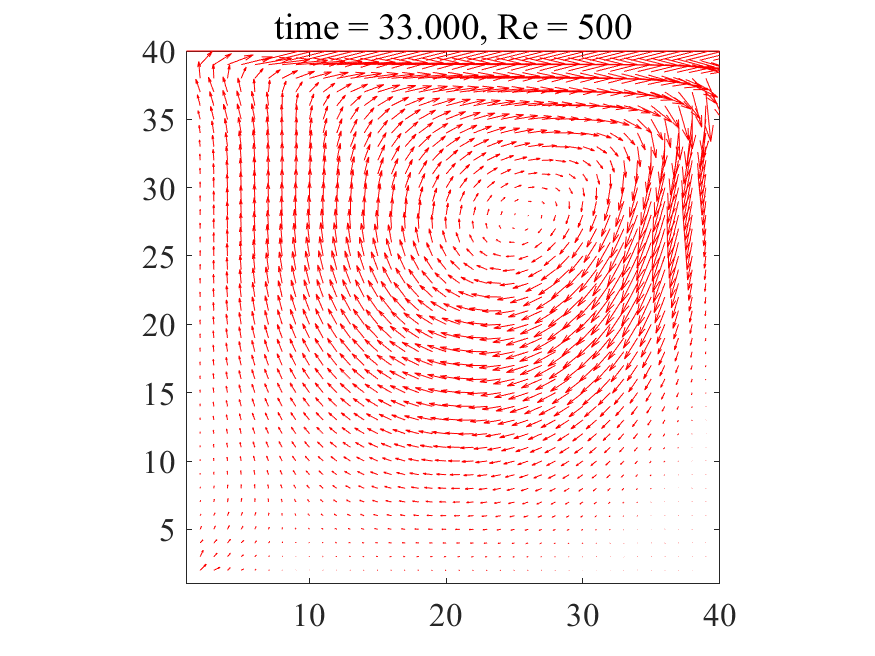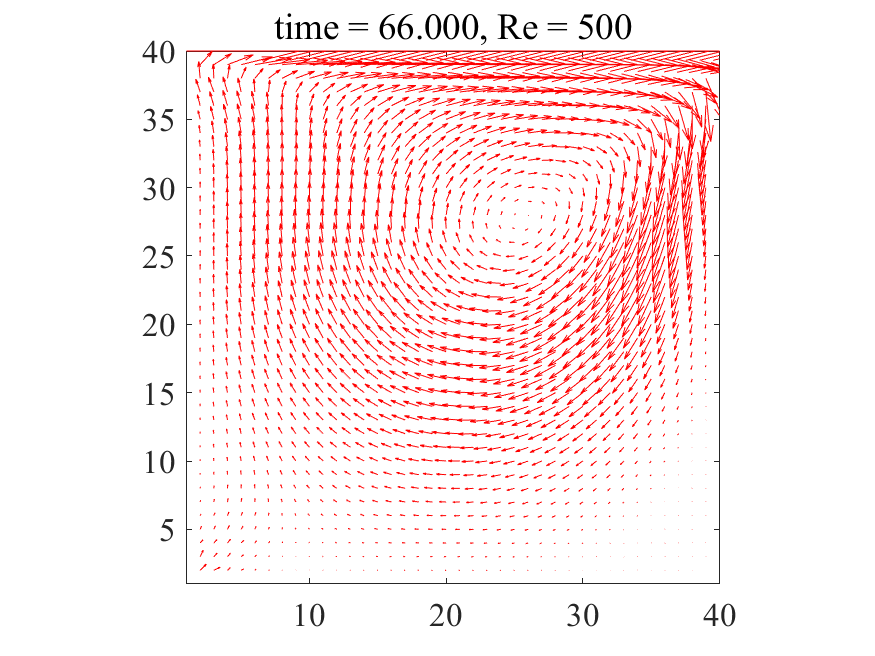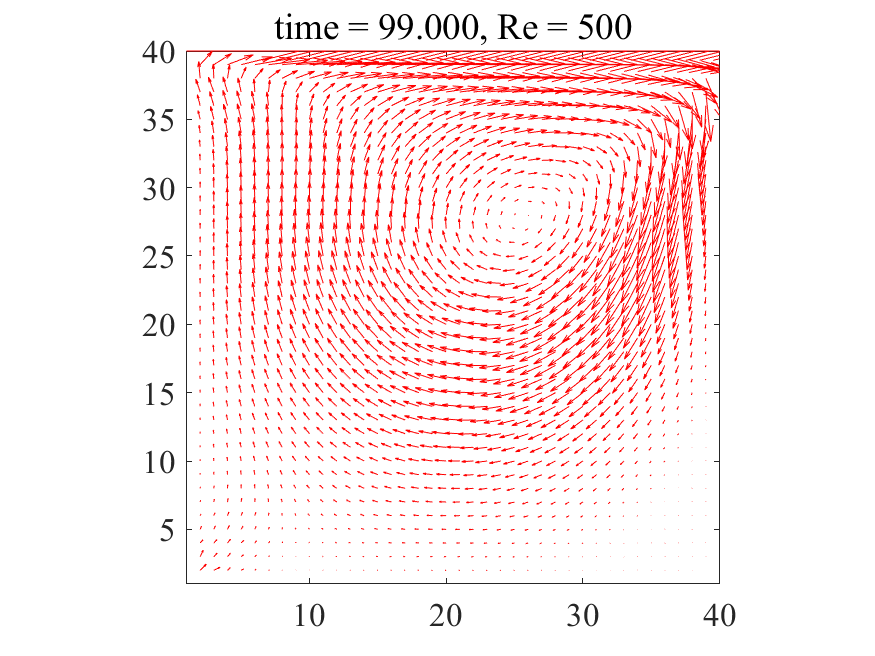
上図より典型的なキャビティ流れが生じていることが分かります。どうやら大外れのプログラムを書いたわけではなさそうです。次に\(\rm{Re}=1,500,1000\)の三通りについて、最終的に得られた流れ場を並べてみます。
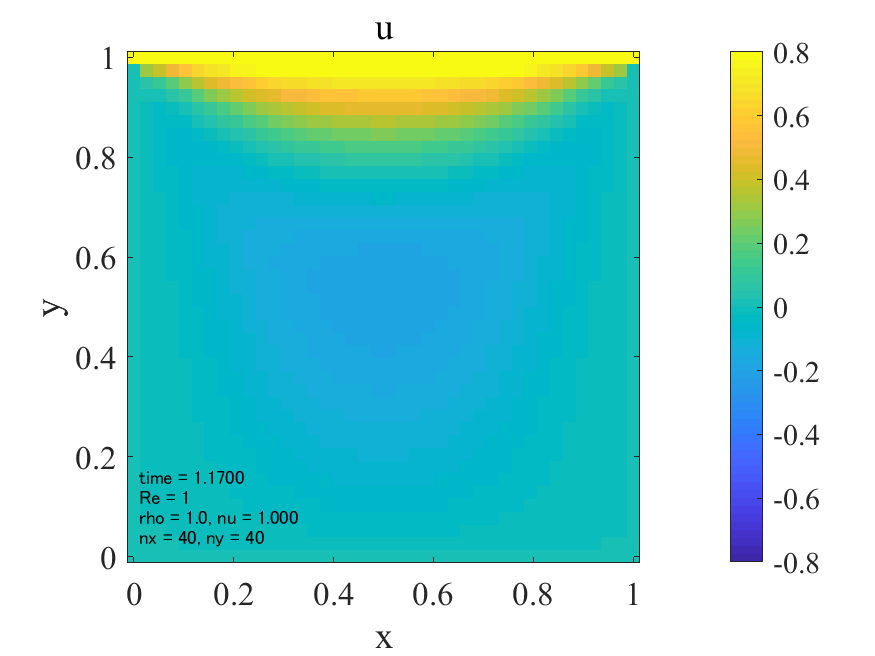
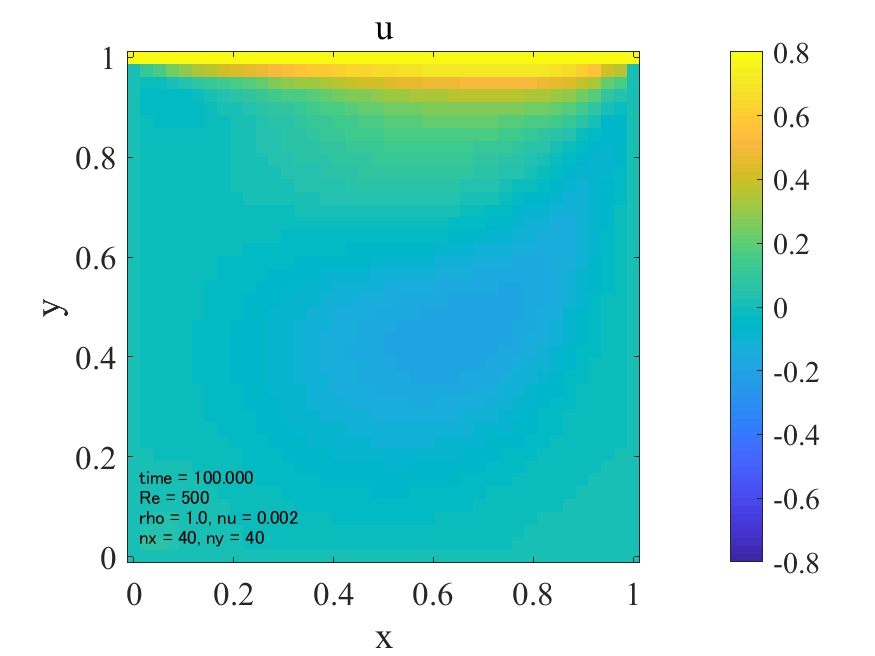
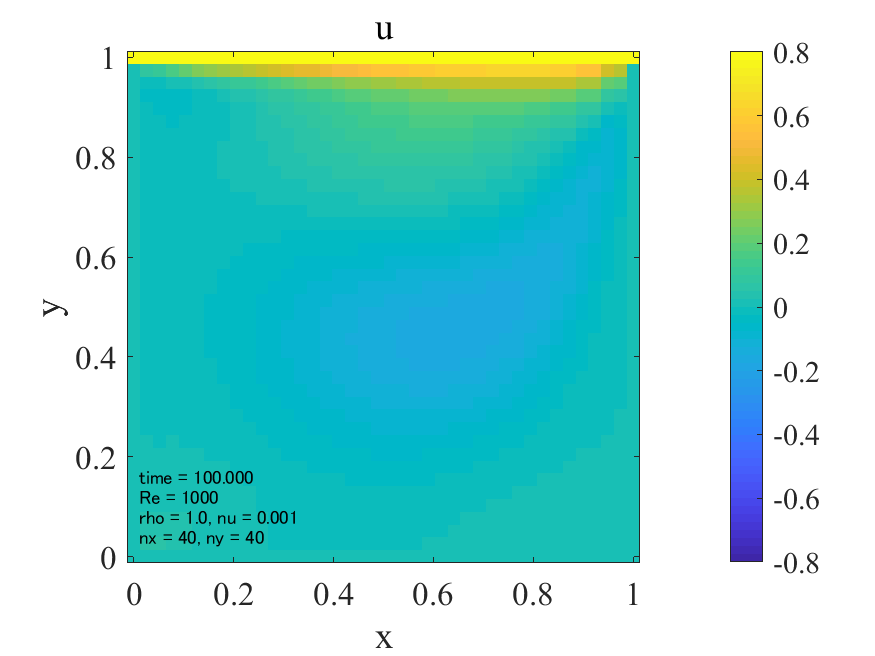
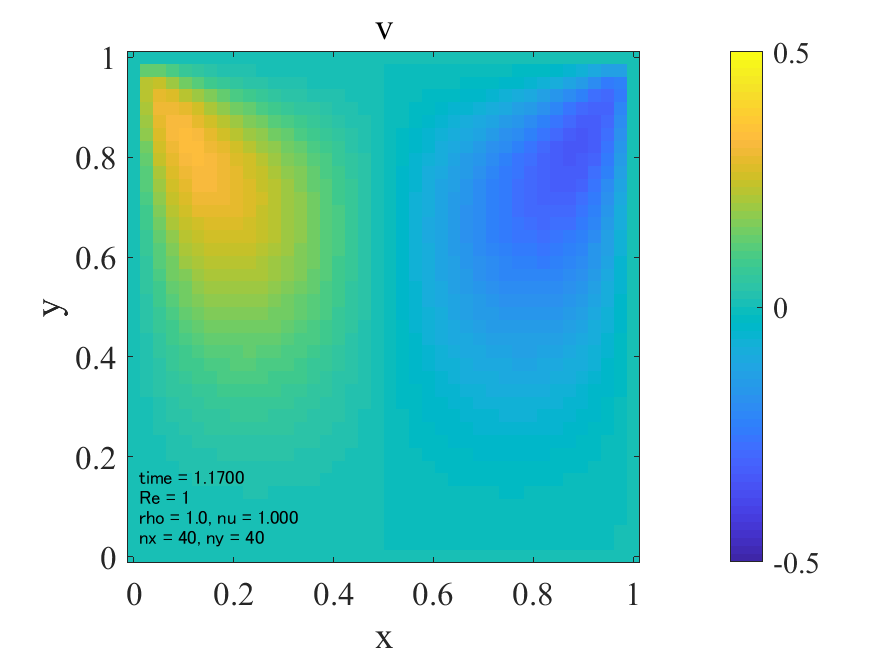
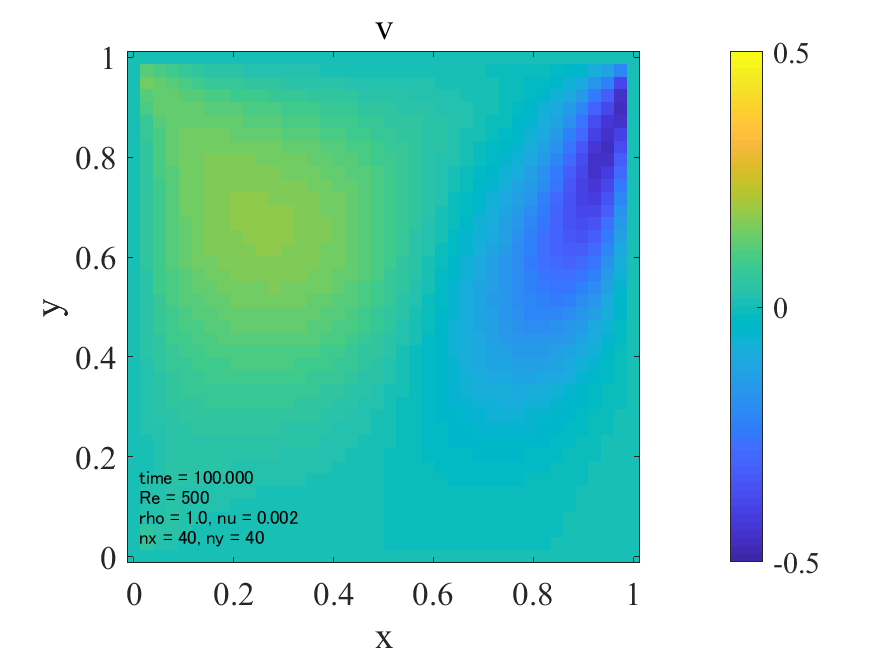
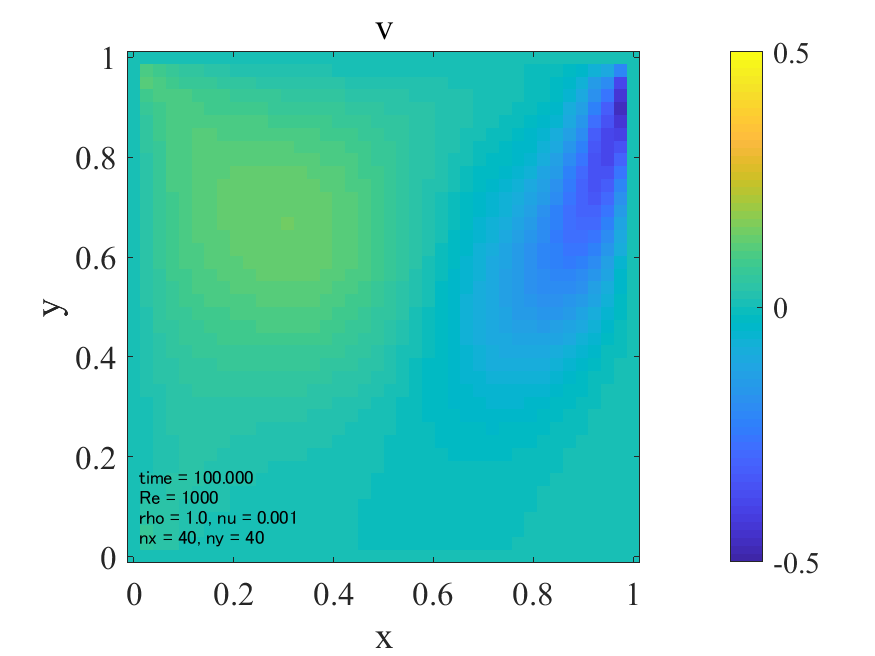
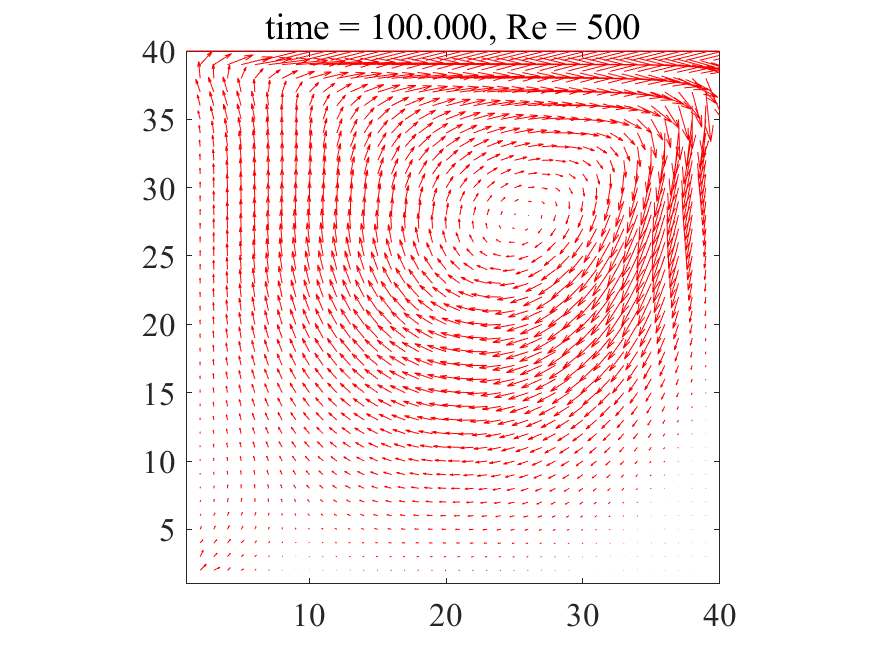
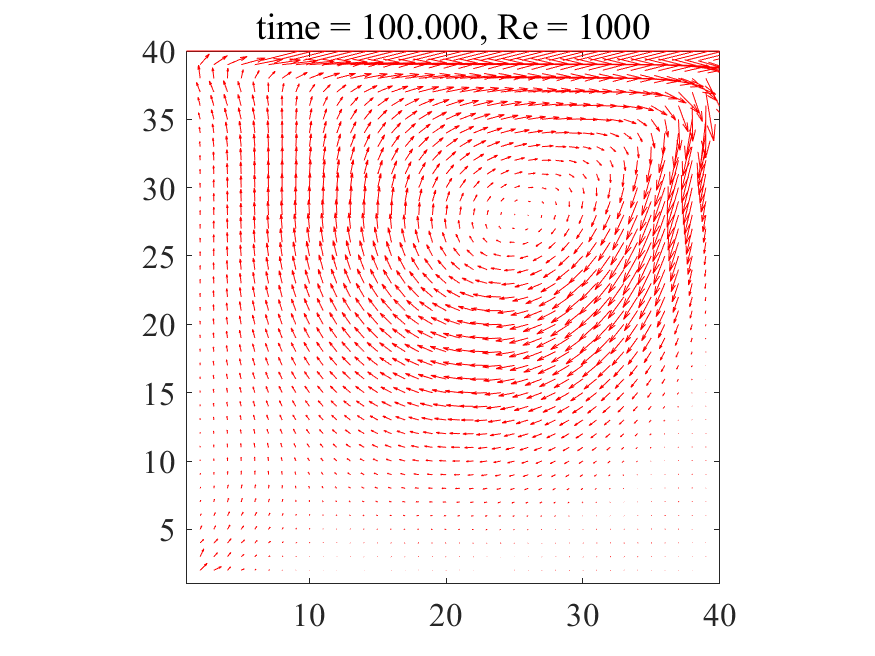
\(\rm{Re}=1\)の場合、流速\(u,v\)が他の2ケースに比べて、上側の壁から広い範囲に広がっています。これは動粘性係数が大きいため、流速の伝播が移流によるものより拡散によるものが支配的であるためと考えられます。(そもそもレイノズル数とは移流項と粘性項のオーダーの比でした。)拡散現象には方向性はないので、流速の分布は対称となり、渦は領域中央付近に生じるものと考えられます。
一方で\(\rm{Re}=500,1000\)になると、上側の壁から流速が拡散される領域が小さくなり、渦が右に寄っている様子が確認できます。これは動粘性係数が小さくなり、流速の伝播が拡散によるものより移流によるものが支配的になったためと考えられます。
不可解なのはレイノズル数が500と1000の間で流れ場にそれほど差が無いように見える点でしょうか。本来であればレイノズル数が上がるほど、渦は扁平形状から綺麗なリング状に転じ、二次渦が生じるはずです。(penguinitisさんのサイトの結果[1]などが分かりやすい。)
もう少し定量的に分析するため、Ghia らの数値解析結果[2]をベンチマークに領域中心の流速について計算結果をプロットしてみました。
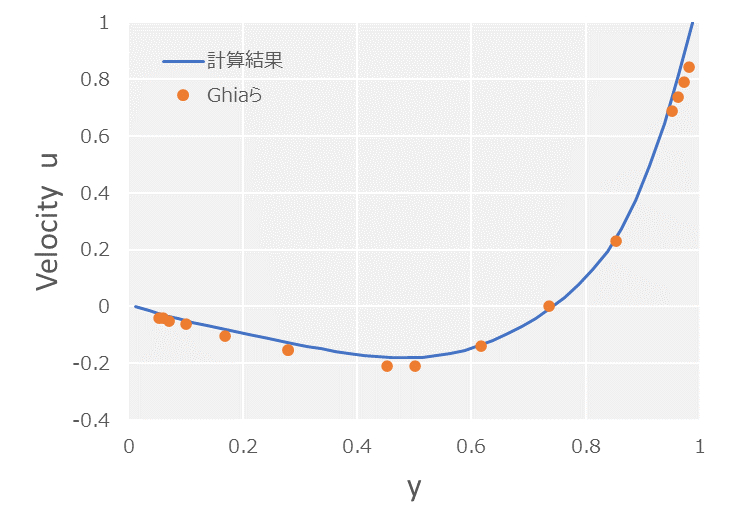
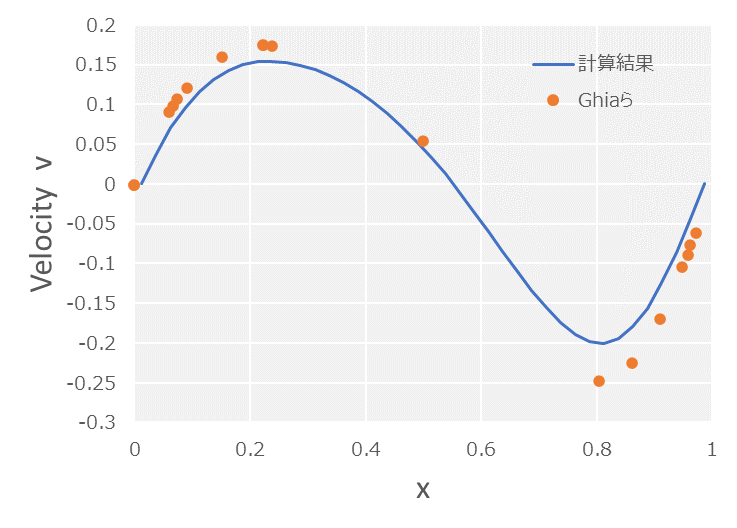
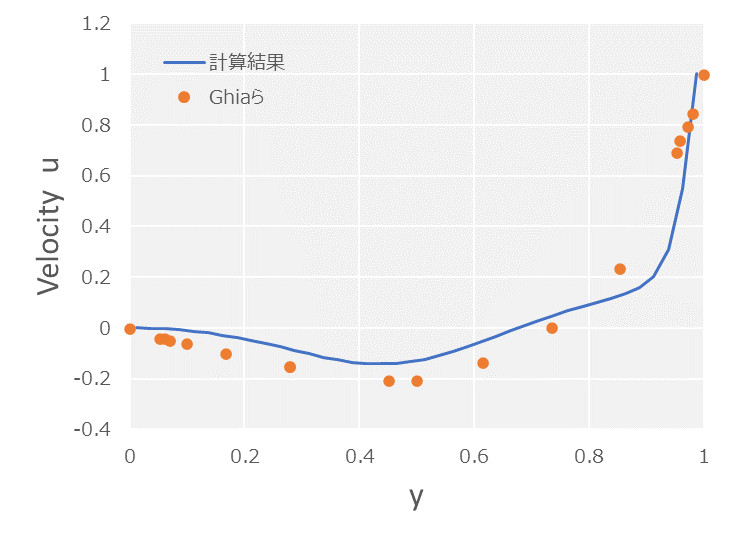
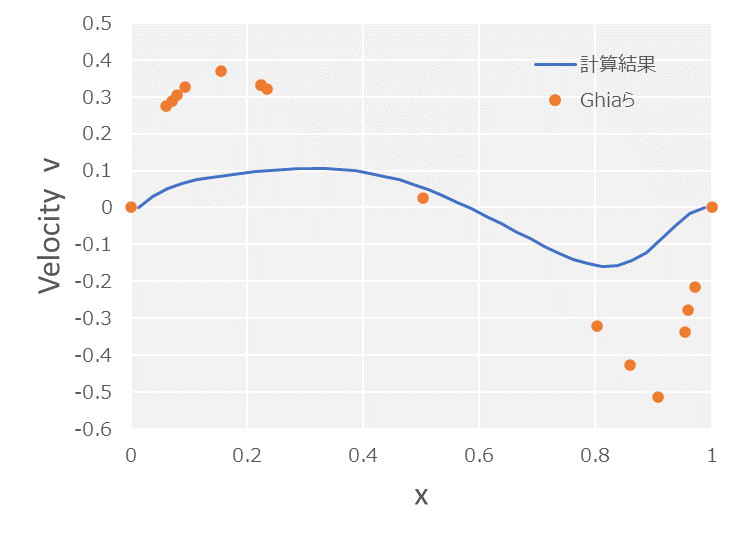
このようにみると\(\rm{Re}=500\)の場合は、そこそこベンチマークと結果が一致していますが、\(\rm{Re}=1000\)の場合、特に\(v\)方向の流速は比較的大きな誤差が生じてしまっていることがわかります。また両方のケースに共通して、計算結果はベンチマークよりピークが鈍る方向へ誤差が生じています。これは数値拡散が及ぼす典型的な結果と考えられます。
今回実装したプログラムでは移流スキームに1次風上差分法を用いていました。このスキームは中心差分法と比較し、計算安定性を有しますが、数値拡散の影響が強く出ることが知られています。したがって、現状のプログラムでは移流項の影響が強く表れる高レイノズル数領域を正しく計算するのは難しいと考えられます。より精度の高い計算にはCIPやWENOといったより高度な移流スキームが必要と思われます。(そもそもメッシュ解像度が足りない等、他にもさまざま原因はありそうですが…)
おわりに
今回はコロケート格子でキャビティフローの実装を行い、ベンチマークとの比較を行いました。現状のベーシックな実装でも低レイノズル数領域でベンチマークとそこそこな一致を見せてくれたのは安心しました。一方で高レイノルズ数領域に関しては改善が必要で、移流スキーム、ポアソン方程式の求解手法、陰解法化などまだまだ勉強すべきことは多いということも実感できました。今後気長に改良を重ねていこうと思います。ひとまず今回はこの辺で。ではでは。
参考文献
[1] 春日 悠, 「キャビティ流れ解析」, penguinitis, 2016年5月7日, http://penguinitis.g1.xrea.com/study/OpenFOAM/cavity/cavity.html
[2] U. Ghia, K. N. Ghia and C. T. Shin: High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method, Journal of Computational Physics, 48, 387-411 (1982).


