はじめに
今回は非線形移流スキームの一種であるTHINC(tangent of hyperbola for interface capturing)法についてまとめたいと思います。THINC法は肖教授ら(2022現在、東京工業大学所属)によって開発され[1]、シンプルなアルゴリズムにもかかわらず、強力な界面保存特性を有しているのが特徴です。今回は手始めに1次元系で実装してTHINC法の雰囲気をつかんでみたいと思います。
VOF法における移流方程式
VOF法では界面を表現するのに、以下のヘビサイトステップ関数型の特性関数\(\chi(x)\)を利用します。
\begin{equation}
\chi(x)=
\begin{cases}
1 & 点xが液体の場合 \\
0 & 点xが気体の場合
\end{cases}
\tag{1}
\end{equation}
ここで\(\chi(x)\)は連続空間上の点\(x\)で定義される値であり、差分法や有限体積法で離散化された空間上のセル中心の値ではないことに注意してください。また、セル\(i\)内で定義される特性関数を\(\chi_i(x)\)と書くことにします。
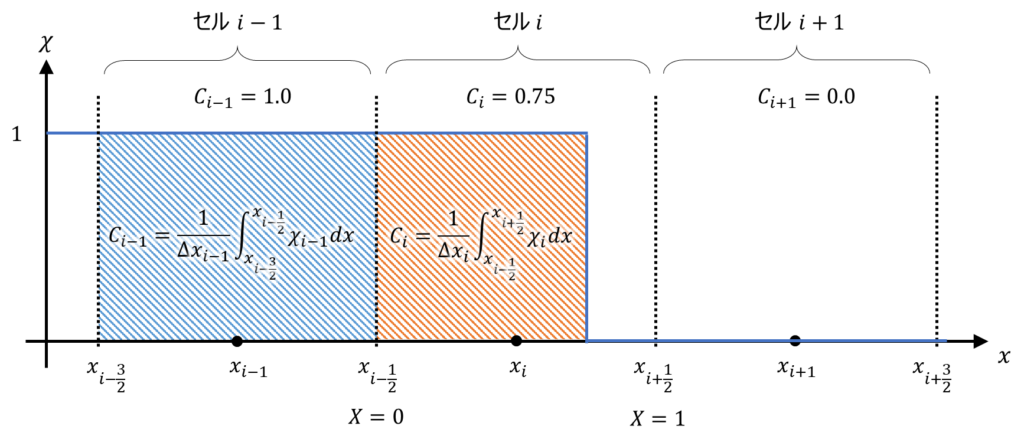
実際の計算は離散化したセル中心で行われるので、セル内の\(\chi(x)\)をセル中心に代表させた値、いわゆるVOF値として表現する必要があります。VOF値はそのセル内の液体の体積分率を示します。セル\(i\)におけるVOF値\(C_{i}\)は以下のように特性関数\(\chi(x)\)の体積平均として表されます。
C_{i}=\frac{1}{\Delta x}\int_{\Omega _i}\chi_i(x)dx
\tag{2}
\end{align}
ここで\(\Omega _i\)は以下の通りセル\(i\)の範囲を表しています。
\Omega _{i}=\left\{x\mid x_{i-\frac{1}{2}}\leq x \leq x_{i+\frac{1}{2}} \right\}
\tag{3}
\end{align}
\(\chi(x)\)は0か1の値しか持ちませんが、VOF値は\(0\leq C_{i} \leq 1\)の値を持ちます。
以下に\(\chi _{i}(x), C_{i}\)の関係を1次元で表した模式図を示します。
特性関数は以下の移流方程式に従うものとします。
\frac{\partial \chi}{\partial t}+\frac{\partial (u \chi)}{\partial x}-\chi\frac{\partial u}{\partial x}=0\tag{4}
\end{align}
左辺第三項は流速の湧き出しに対応する項で、非圧縮性流体を扱う場合には0になります。イメージ的にはあるセルから気体または液体が湧き出したり、吸い込まれたりするイメージです。スタンダードなVOF法ではこの項は無視されますが、THINC法の原論文では上式のようにより一般的な形で特性関数の輸送方程式が定式化されています。(このような形式を「非ソレノイド場」における移流方程式と呼ぶらしい。[2])
上式についてセル\(i\)内で体積平均をとり、式\((2)\)を代入することでVOF値の移流方程式が得られます。
&\frac{1}{\Delta x}\int_{x_{i-\frac{1}{2}}} ^{x_{i+\frac{1}{2}}} \frac{\partial \chi_{i}}{\partial t}dx+\frac{1}{\Delta x}\int_{x_{i-\frac{1}{2}}} ^{x_{i+\frac{1}{2}}}\left\{\frac{\partial (u \chi)}{\partial x}\right\}_{i}dx-\frac{1}{\Delta x}\int_{x_{i-\frac{1}{2}}} ^{x_{i+\frac{1}{2}}}\chi_{i}\left(\frac{\partial u}{\partial x}\right)_{i}dx=0\\
&\Leftrightarrow
\frac{\partial}{\partial t}\left(\frac{1}{\Delta x}\int_{x_{i-\frac{1}{2}}} ^{x_{i+\frac{1}{2}}} \chi_{i} dx \right)+\frac{1}{\Delta x}\int_{x_{i-\frac{1}{2}}} ^{x_{i+\frac{1}{2}}}\left\{\frac{\partial (u \chi)}{\partial x}\right\}_{i}dx-\left(\frac{\partial u}{\partial x}\right)_{i}\frac{1}{\Delta x}\int_{x_{i-\frac{1}{2}}} ^{x_{i+\frac{1}{2}}+\frac{1}{2}}\chi_{i}dx=0\\
&\Leftrightarrow
\frac{\partial C_{i}}{\partial t}+\frac{1}{\Delta x}Q_{i}-\left(\frac{\partial u}{\partial x}\right)_{i}C_{i}=0
\tag{5}
\end{align}
ここで各セル内の流速(および流速勾配)はセル中心の値で代表させることとして、\(\left(\frac{\partial u}{\partial x}\right)_{i}\)は一定として扱っています。このように流速は各セル内で変化しないとするのに、特性関数は各セル内でも連続的に変化するものとして取り扱うのは若干わかりずらいところです。
また左辺第二項\(Q_{i}\)は以下の積分を表しています。
Q_{i}=\int_{x_{i-\frac{1}{2}}} ^{x_{i+\frac{1}{2}}}\left\{\frac{\partial (u \chi)}{\partial x}\right\}_{i}dx\tag{6}
\end{align}
この項は単位時間当たりにセル内に入ってくるフラックスとセル内から出ていくフラックスの収支を表しています。式\((6)\)の被積分関数を\(f(x)\)で表すと以下のように変形できます。
Q_{i}=\int_{x_{i-\frac{1}{2}}} ^{x_{i+\frac{1}{2}}}\left\{\frac{\partial (u \chi)}{\partial x}\right\}_{i}dx=\left[ f(x)\right]_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}= f(x_{i+\frac{1}{2}}) – f(x_{i-\frac{1}{2}})\tag{7}
\end{align}
したがって、式\((5)\)は以下のように書けます。
\frac{\partial C_{i}}{\partial t}+\frac{f(x_{i+\frac{1}{2}}) – f(x_{i-\frac{1}{2}})}{\Delta x}-\left(\frac{\partial u}{\partial x}\right)_{i}C_{i}=0
\tag{8}
\end{align}
さらに上式について時間・空間に関して離散化すると以下の式が得られます。
&\frac{C_{i}^{n+1}-C_{i}^{n}}{\Delta t}+\frac{f^{n}(x_{i+\frac{1}{2}})- f^{n}(x_{i-\frac{1}{2}})}{\Delta x}-C_{i}^{n}\frac{u_{i+\frac{1}{2}}^{n}-u_{i-\frac{1}{2}}^{n}}{\Delta x}=0\\
&\Leftrightarrow
C_{i}^{n+1}=C_{i}^{n}-\frac{f^{n}(x_{i+\frac{1}{2}})- f^{n}(x_{i-\frac{1}{2}})}{\Delta x}\Delta t+C_{i}^{n}\frac{u_{i+\frac{1}{2}}^{n}-u_{i-\frac{1}{2}}^{n}}{\Delta x}\Delta t\\
&\Leftrightarrow
C_{i}^{n+1}=C_{i}^{n}-\frac{F^{n}_{i+\frac{1}{2}}- F^{n}_{i-\frac{1}{2}}}{\Delta x}+C_{i}^{n}\frac{u_{i+\frac{1}{2}}^{n}-u_{i-\frac{1}{2}}^{n}}{\Delta x}\Delta t
\tag{9}
\end{align}
上式がVOF値の離散化された時間発展式です。\(F^{n}_{i+\frac{1}{2}}\)は以下の通りです。
F^{n}_{i-\frac{1}{2}}=f^{n}(x_{i-\frac{1}{2}})\Delta t\\
F^{n}_{i+\frac{1}{2}}=f^{n}(x_{i+\frac{1}{2}})\Delta t\\
\tag{10}
\end{align}
式\((9)\)で\(C\)の時間発展を解くことで、界面の時間変化が分かります。
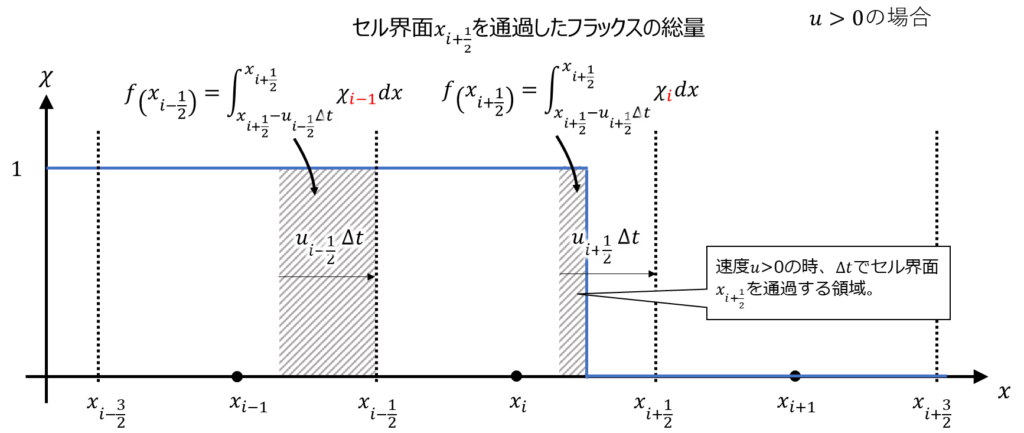
では結局、右辺第二項の\(F^{n}_{i+\frac{1}{2}},F^{n}_{i-\frac{1}{2}}\)をどのように計算されるのでしょうか?例えば\(F^{n}_{i+\frac{1}{2}}\)は\(\Delta t\)の間にセル界面\(x_{i+\frac{1}{2}}\)を通過するVOF値の総量を示すのでした。したがって、\(u>0\)の時、以下の積分として表現できます。
F^{n}_{i+\frac{1}{2}}=\int_{x_{i+\frac{1}{2}}-u_{i+\frac{1}{2}}\Delta t} ^{x_{i+\frac{1}{2}}} \chi _i dx
\tag{11}
\end{align}
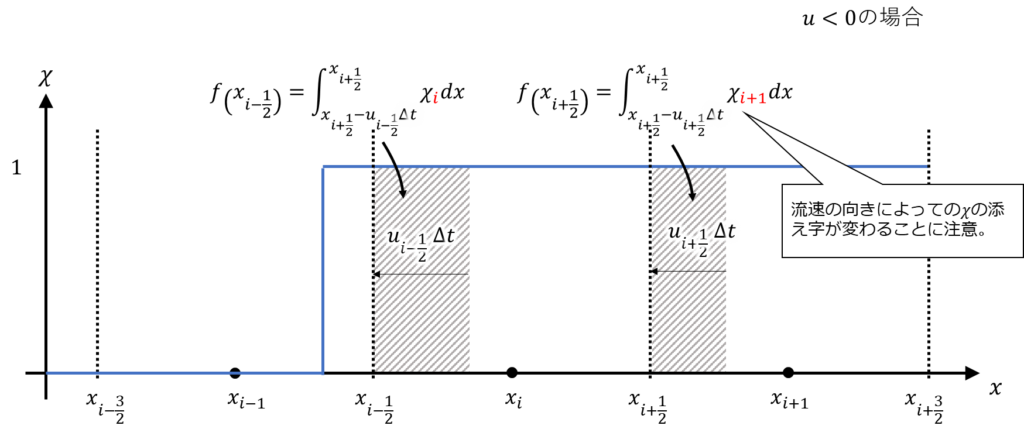
\(u<0\)の場合は\(\chi\)の添え字がひとつずれて以下のようになります。
F^{n}_{i+\frac{1}{2}}=\int_{x_{i+\frac{1}{2}}-u_{i+\frac{1}{2}}\Delta t} ^{x_{i+\frac{1}{2}}} \chi _{i+1} dx
\tag{12}
\end{align}
式\((11),(12)\)をまとめると以下のように書けます。
F_{i+\frac{1}{2}}=f^{n}(x_{i+\frac{1}{2}}) \Delta t=\int_{x_{i+\frac{1}{2}}-u_{i+\frac{1}{2}}\Delta t} ^{x_{i+\frac{1}{2}}} \chi _{is} dx
\tag{13}
\end{align}
\begin{equation}
is=
\begin{cases}
i & u_{i+\frac{1}{2}}\geq 0の場合\\
i + 1 & u_{i+\frac{1}{2}}<0の場合
\end{cases}
\tag{14}
\end{equation}
\(F_{i-\frac{1}{2}}\)場合も同様に考えます。\(u>0\)の時、以下の積分として表現できます。
F^{n}_{i-\frac{1}{2}}=\int_{x_{i-\frac{1}{2}}-u_{i-\frac{1}{2}}\Delta t} ^{x_{i-\frac{1}{2}}} \chi _{i – 1}dx
\tag{15}
\end{align}
\(u<0\)の場合は\(\chi\)の添え字がひとつずれて以下のようになります。
F^{n}_{i-\frac{1}{2}}=\int_{x_{i-\frac{1}{2}}-u_{i-\frac{1}{2}}\Delta t} ^{x_{i-\frac{1}{2}}} \chi _{i}dx
\tag{16}
\end{align}
式\((15),(16)\)をまとめると以下のように書けます。
F_{i-\frac{1}{2}}=f^{n}(x_{i-\frac{1}{2}}) \Delta t=\int_{x_{i-\frac{1}{2}}-u_{i-\frac{1}{2}}\Delta t} ^{x_{i-\frac{1}{2}}} \chi _{is} dx
\tag{17}
\end{align}
\begin{equation}
is=
\begin{cases}
i -1& u_{i-\frac{1}{2}}\geq 0の場合\\
i & u_{i-\frac{1}{2}}<0の場合
\end{cases}
\tag{18}
\end{equation}
式\((14)\)と式\((18)\)で\(is\)の番号が一つずれることに注意しましょう。
以上より、\(F_{i+\frac{1}{2}},F_{i-\frac{1}{2}}\)を得ることが出来るので、式\((9)\)からVOF値の時間発展を追うことが可能です。
VOF法の中でもSLIC法などは特性関数としてヘビサイド関数を用いますが、これにより複雑な界面再構成操作が生じ実装を難しくするという課題があるようです。この辺は奥が深そうなので、追々勉強できればと思います。
THINC法における特性関数
VOF法では特性関数としてヘビサイドステップ関数(式\((1)\))を用いました。一方、THINC法では\(i\)番目のセルの特性関数として以下のような\(\tanh\)関数を用います。
\begin{equation}
\chi _i =\frac{1}{2}\left [ 1 + \alpha _{i}\tanh \left\{ \beta \left(\frac{x -x_{i-\frac{1}{2}}}{\Delta x}-d_{i}\right)\right\}\right ]
\tag{19}
\end{equation}
\(\tanh\)に含まれる\(\frac{x -x_{i-\frac{1}{2}}}{\Delta x}\)は\(i\)番目のセル空間を規格化して\(0\sim 1\)の範囲で表すことを意味しています。
ここで\(\alpha_i\)は界面の向きによって変化するパラメーターであり、以下のように表現されます。
\begin{equation}
\alpha _{i}=
\begin{cases}
1 & C_{i+1}\geq C_{i-1}の場合\\
-1 & C_{i+1}<C_{i-1}の場合
\end{cases}
\tag{20}
\end{equation}
\(X=\frac{x -x_{i-\frac{1}{2}}}{\Delta x}\)と規格化した状態で\(\alpha = -1,1\)の2パターンでグラフ書くと以下のようになります。
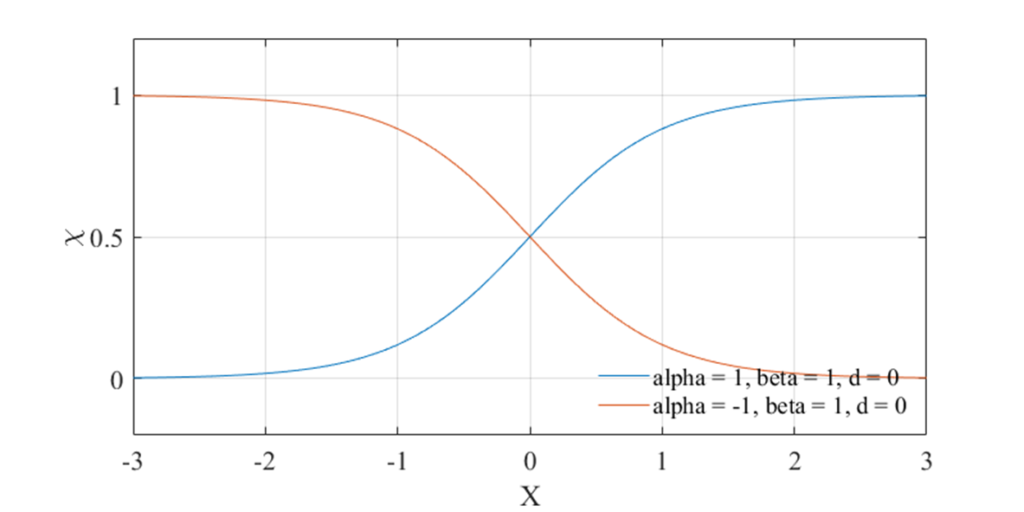
また\(\beta\)は界面の厚みを表すパラメーターです。\(\beta\)が大きくなるほど\(\tanh\)関数のカーブは急峻に、小さくなるほど緩やかになります。原著論文[1]では暫定的な値として\(\beta=3.5\)が用いられています。
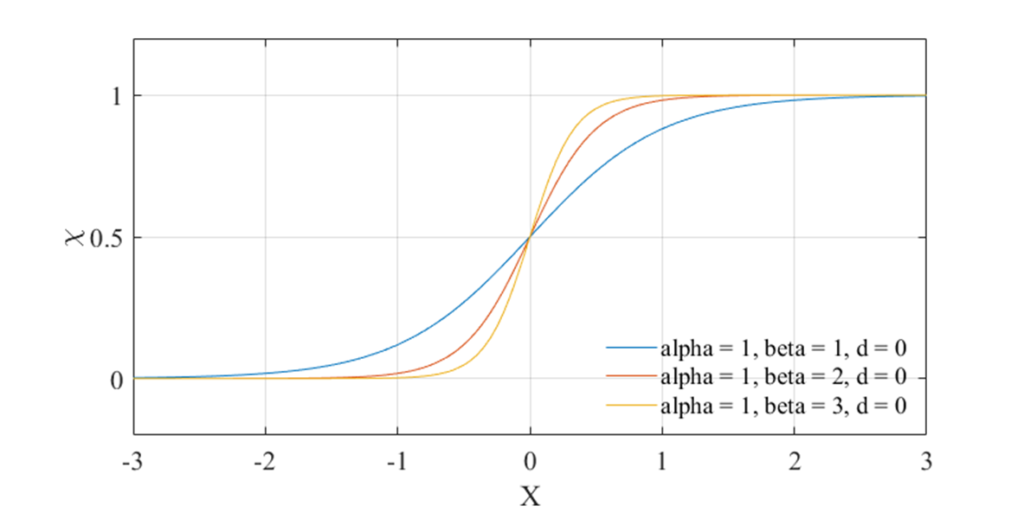
\(d_{i}\)は界面の位置を表します。実際には\(\chi_i=0.5\)の位置です。
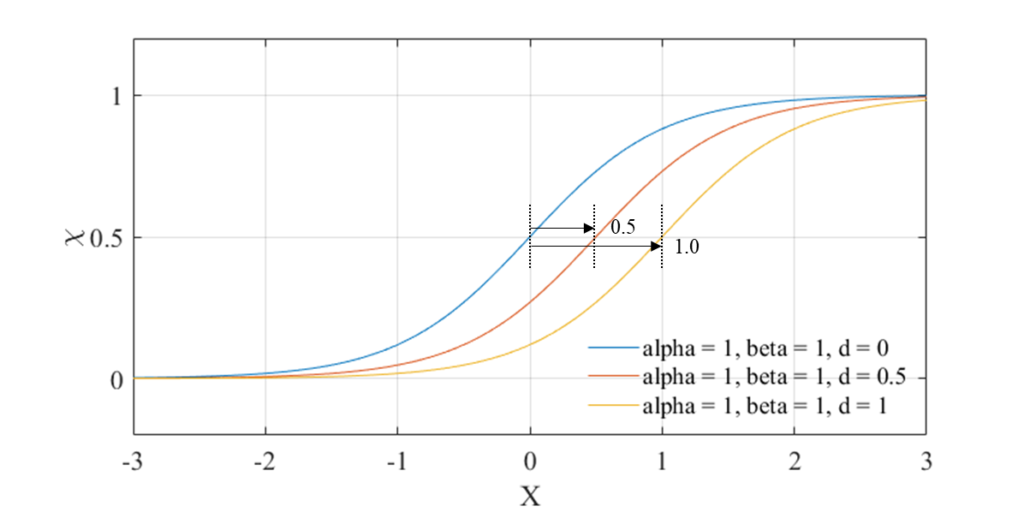
THINC法では以上のパラメーターを有する\(\tanh\)型の特性関数を用いることでVOF値の時間発展を解いていきます。このような滑らかな特性関数を用いることで、一般的なVOF法で現れる界面付近で不自然に孤立した流体(「flotsam(浮遊物)」)を防ぐことが出来るらしいです。
界面位置\(d\)の計算
さて式\((19)\)のように\(\chi\)の形が決まったので次は式\((13),(17)\)の積分を実行しフラックスを求めたいのですが、そもそも式\((19)\)の中の界面位置\(d_i\)はどのように求めるのでしょうか?
実は初期の界面状態(VOF値\(C_{i}\))が与えられれば、以下のような手順で\(d_{i}\)を求めることが出来ます。
式\((2)\)に式\((19)\)を代入するとTHINC法におけるVOF値は以下のように書けます。
C_{i}=\frac{1}{\Delta x}\int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\frac{1}{2}\left [ 1 + \alpha _{i}\tanh \left\{ \beta \left(\frac{x -x_{i-\frac{1}{2}}}{\Delta x}-d_{i}\right)\right\}\right ]dx
\tag{21}
\end{align}
\(X=\frac{x -x_{i-\frac{1}{2}}}{\Delta x}\)とおいて\(i\)番目のセル空間を規格化すると以下のように変形できます。
C_{i}=\frac{1}{2}\int_{0}^{1}\ 1 + \alpha _{i}\tanh\left\{ \beta \left(X-d_{i}\right)\right\}dX
\tag{22}
\end{align}
最終的には\(d_{i}\)は以下のように書けます。
d_{i}=\frac{1}{2\beta}\log \left(\frac{a_{3}(a_{3}-a_{1})}{a_{1}a_{3}-1}\right)\tag{23}
\end{align}
ここで\(a_{1},a_{3}\)は下記のとおりです。
a_{1}=\exp\left[{\frac{\beta \left(2C_{i} – 1\right)}{\alpha _{i}}}\right]\tag{24}\\
\end{align}
a_{3}=\exp(\beta)
\tag{25}
\end{align}
式\((18)\)の積分を実行します。
&C_{i}=\frac{1}{2}\int_{0}^{1}\ 1 + \alpha _{i}\tanh\left\{ \beta \left(X-d_{i}\right)\right\}dX\\
&\Leftrightarrow
C_{i}=\frac{1}{2}\left [ X + \frac{\alpha _{i}}{\beta}\log\left\{\cosh\left( \beta \left(X-d_{i}\right)\right)\right\}\right ]_{0}^{1}\\
&\Leftrightarrow
C_{i}=\frac{1}{2}\left [ 1 + \frac{\alpha _{i}}{\beta}\log\left\{\frac{\cosh\left( \beta -\beta d_{i}\right)}{\cosh\left( -\beta d_{i}\right)}\right\}\right ]\\
&\Leftrightarrow
\frac{\beta \left(2C_{i} – 1\right)}{\alpha _{i}}= \log\left\{\frac{\cosh\left( \beta -\beta d_{i}\right)}{\cosh\left( -\beta d_{i}\right)}\right\}\\
&\Leftrightarrow
\frac{\beta \left(2C_{i} – 1\right)}{\alpha _{i}}= \log\left\{\frac{\cosh\left( \beta -\beta d_{i}\right)}{\cosh\left( \beta d_{i}\right)}\right\}\\
&\Leftrightarrow
\exp\left[{\frac{\beta \left(2C_{i} – 1\right)}{\alpha _{i}}}\right]= \frac{\cosh\left( \beta -\beta d_{i}\right)}{\cosh\left( \beta d_{i}\right)}\\
&\Leftrightarrow
\exp\left[{\frac{\beta \left(2C_{i} – 1\right)}{\alpha _{i}}}\right]= \frac{\exp\left( -\beta +\beta d_{i}\right)+\exp\left(\beta -\beta d_{i}\right)}{\exp\left( -\beta d_{i}\right)+\exp\left(\beta d_{i}\right)}\tag{A1}\\
\end{align}
ここで以下のように\(a_{1},a_{2},a_{3}\)を定義します。
a_{2}=\exp(\beta d_{i})
\tag{A2}
\end{align}
a_{3}=\exp(\beta)
\tag{A3}
\end{align}
&a_{1}=\frac{\exp\left( -\beta +\beta d_{i}\right)+\exp\left(\beta -\beta d_{i}\right)}{\exp\left( -\beta d_{i}\right)+\exp\left(\beta d_{i}\right)}\\
&\Leftrightarrow
a_{1}=\frac{\frac{a_{2}}{a_{3}}+\frac{a_{3}}{a_{2}}}{\frac{1}{a_{2}}+a_{2}}\\
&\Leftrightarrow
a_{1}=\frac{a_{2}^2+a_{3}^2}{a_{3}(1+a_{2}^2)}\left(=\exp\left[{\frac{\beta \left(2C_{i} – 1\right)}{\alpha _{i}}}\right]\right)\tag{A4}\\
\end{align}
式\((\rm{A4})\)について\(a_2=\)の形でまとめます。
&a_{1}=\frac{a_{2}^2+a_{3}^2}{a_{3}(1+a_{2}^2)}\\
&\Leftrightarrow
a_{1}a_{3}(1+a_{2}^2)=a_{2}^2+a_{3}^2\\
&\Leftrightarrow
a_{1}a_{3}+a_{1}a_{3}a_{2}^2=a_{2}^2+a_{3}^2\\
&\Leftrightarrow
a_{1}a_{3}a_{2}^2-a_{2}^2=a_{3}^2-a_{1}a_{3}\\
&\Leftrightarrow
a_{2}^2=\frac{a_{3}(a_{3}-a_{1})}{a_{1}a_{3}-1}\tag{A5}\\
\end{align}
上式について式\((\rm{A2})\)を用いて\(a_2\)を元に戻します。
&\exp(2\beta d_{i})=\frac{a_{3}(a_{3}-a_{1})}{a_{1}a_{3}-1}\\
&\Leftrightarrow
d_{i}=\frac{1}{2\beta}\log \left(\frac{a_{3}(a_{3}-a_{1})}{a_{1}a_{3}-1}\right)\tag{A6}
\end{align}
以下に\(C_{i}=0.75\)の時の界面位置のイメージ図を記載します。ちょうど界面位置に\(d_{i}\)を設定することで、\(\chi_{i}\)で矩形領域を近似し、そのセル平均値として\(C_{i}=0.75\)を表現していることが分かります。
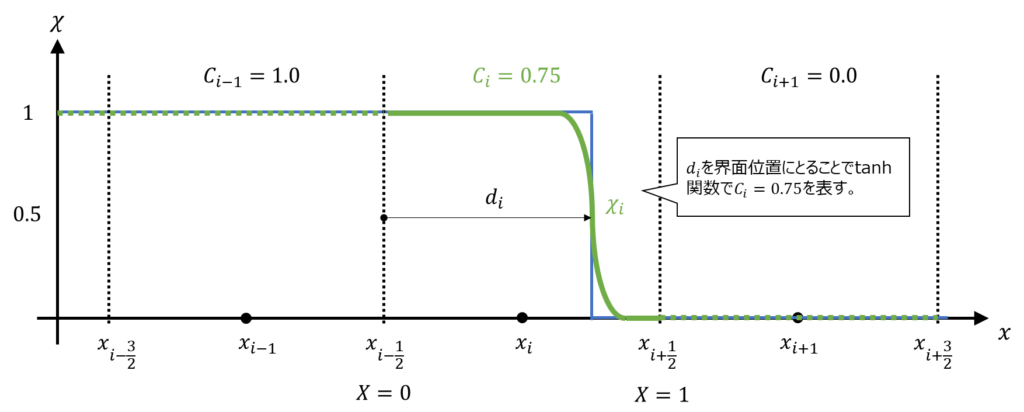
ここで注意したいのは\(C=1,0\)の時、式\((23)\)の\(d_{i}\)は発散してしまう点です。
例えば\(C_{i-1}=1\)の場合、\(\alpha = -1\)とすると、\(a_{1}=\exp(-\beta)\)なので、\(a_{1}a_{3}=1\)となります。この為、式\((23)\)において0除算が発生し、\(d→ +\infty\)となります。このことは\(d\)をできるだけ大きくとることで\(\tanh\)関数で\(\chi=1.0\)を表そうとしていることを示しています。
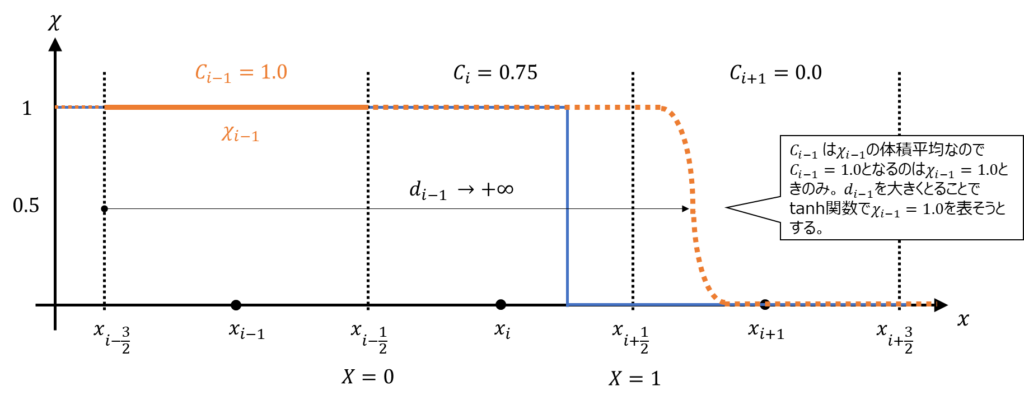
このような場合、このまま計算すると破綻してしまうので、\(\chi\)に式\((19)\)のような\(\tanh\)関数を用いるのではなく、素直に\(\chi=1\)として計算してしまうのが良いでしょう。
同様に\(C_{i-1}=0\)の場合、\(a_{1}=\exp(\beta)\)なので、\(a_{1}-a_{3}=0\)となります。この為、式\((23)\)において分子に0が発生し、\(d→ -\infty\)となります。このことは\(d\)をできるだけ小さくとることで\(\tanh\)関数で\(\chi=0\)を表そうとしていることを示しています。
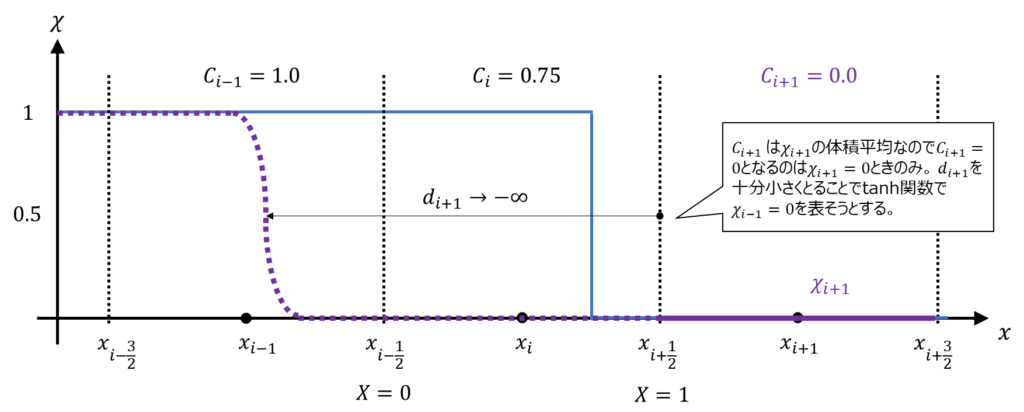
このような場合は\(\chi=0\)として計算するのが良いでしょう。
もともと界面位置\(d\)を求めるのは、フラックスを求めるためでした。セルが気相または液相で満ちてる場合(\(C=0,1\))は、フラックスは流速だけから決まるので、わざわざ複雑な特性関数の積分から求める必要はないわけです。
各セル境界でのフラックスを計算する際、式\((14)、(18)\)のように流速の向きに応じて、左右どちらのセルのを参照するかは\(is\)で定義されるのでした。これを踏まえて、ここまでの結果をまとめると以下の通りです。
| \(0<C_{is}<1\)の場合 | 特性関数として\(\tanh\)関数(式\((15)\))を用いて界面位置\(d\)を決定し、これに基づきフラックス\(F\)を計算する |
| \(C_{is}=1\)の場合 | 特性関数として\(\chi=1\)を用いてフラックス\(F\)を計算する。界面位置は計算しない。 |
| \(C_{is}=0\)の場合 | 特性関数として\(\chi=0\)を用いてフラックス\(F\)を計算する。界面位置は計算しない。 |
フラックス\(F\)の計算
では界面位置\(d\)の求め方が分かったので、セル界面のフラックス\(F_{i+\frac{1}{2}},F_{i-\frac{1}{2}}\)を求めていきましょう。\(C_{is}\)の値ごとに場合分けで考えます。
まず\(0<C_{is}<1\)の場合です。この場合、特性関数として式\((19)\)を用いるのでした。式\((13)\)に式\((19)\)を代入し積分を計算します。
&F_{i+\frac{1}{2}}=\int_{x_{i+\frac{1}{2}}-u_{i+\frac{1}{2}}\Delta t} ^{x_{i+\frac{1}{2}}} \frac{1}{2}\left [ 1 + \alpha _{is}\tanh \left\{ \beta \left(\frac{x -x_{is-\frac{1}{2}}}{\Delta x}-d_{is}\right)\right\}\right ] dx\\
&\Leftrightarrow
F_{i+\frac{1}{2}}=\frac{1}{2}\left [ x + \frac{\alpha _{is}\Delta x}{\beta}\log\left\{\cosh \left\{ \beta \left(\frac{x -x_{is-\frac{1}{2}}}{\Delta x}-d_{is}\right)\right\}\right\}\right ] _{x_{i+\frac{1}{2}}-u_{i+\frac{1}{2}}\Delta t} ^{x_{i+\frac{1}{2}}}\\
&\Leftrightarrow
F_{i+\frac{1}{2}}=\frac{1}{2}\left [ u_{i+\frac{1}{2}}\Delta t + \frac{\alpha _{is}\Delta x}{\beta}\log\left\{ \frac{\cosh \left\{ \beta \left(\frac{x_{i+\frac{1}{2}} -x_{is-\frac{1}{2}}}{\Delta x}-d_{is}\right)\right\}}{\cosh \left\{ \beta \left(\frac{x_{i+\frac{1}{2}}-u_{i+\frac{1}{2}}\Delta t -x_{is-\frac{1}{2}}}{\Delta x}-d_{is}\right)\right\}}\right\}\right ] \\
&\Leftrightarrow
F_{i+\frac{1}{2}}=\frac{1}{2}\left [ u_{i+\frac{1}{2}}\Delta t + \frac{\alpha _{is}\Delta x}{\beta}\log\left\{ \frac{\cosh \left\{ \beta \left(\gamma-d_{is}\right)\right\}}{\cosh \left\{ \beta \left(\gamma-\frac{u_{i+\frac{1}{2}}\Delta t }{\Delta x}-d_{is}\right)\right\}}\right\}\right ] \tag{26}\\
\end{align}
\begin{equation}
is=
\begin{cases}
i & u_{i+\frac{1}{2}}\geq 0の場合\\
i + 1 & u_{i+\frac{1}{2}}<0の場合
\end{cases}
\tag{27}
\end{equation}
\(\gamma\)は\(\frac{x_{i+\frac{1}{2}} -x_{is-\frac{1}{2}}}{\Delta x}\)を示しており、以下のように場合分けできます。
\begin{equation}
\gamma=
\begin{cases}
1 & is =i すなわちu_{i+\frac{1}{2}}\geq 0の場合\\
0 & is =i +1 すなわちu_{i+\frac{1}{2}}<0の場合
\end{cases}
\tag{28}
\end{equation}
大分複雑になってしまいましたが、上記が\(x_{i+\frac{1}{2}}\)におけるフラックスです。同様に\(F_{i-\frac{1}{2}}\)についても式\((17)\)に式\((19)\)を代入することで以下のように書けます。
&F_{i-\frac{1}{2}}=\int_{x_{i-\frac{1}{2}}-u_{i-\frac{1}{2}}\Delta t} ^{x_{i-\frac{1}{2}}} \frac{1}{2}\left [ 1 + \alpha _{is}\tanh \left\{ \beta \left(\frac{x -x_{is-\frac{1}{2}}}{\Delta x}-d_{is}\right)\right\}\right ] dx\\
&\Leftrightarrow
F_{i-\frac{1}{2}}=\frac{1}{2}\left [ u_{i-\frac{1}{2}}\Delta t + \frac{\alpha _{is}\Delta x}{\beta}\log\left\{ \frac{\cosh \left\{ \beta \left(\frac{x_{i-\frac{1}{2}} -x_{is-\frac{1}{2}}}{\Delta x}-d_{is}\right)\right\}}{\cosh \left\{ \beta \left(\frac{x_{i-\frac{1}{2}}-u_{i-\frac{1}{2}}\Delta t -x_{is-\frac{1}{2}}}{\Delta x}-d_{is}\right)\right\}}\right\}\right ] \\
&\Leftrightarrow
F_{i-\frac{1}{2}}=\frac{1}{2}\left [ u_{i-\frac{1}{2}}\Delta t + \frac{\alpha _{is}\Delta x}{\beta}\log\left\{ \frac{\cosh \left\{ \beta \left(\gamma-d_{is}\right)\right\}}{\cosh \left\{ \beta \left(\gamma-\frac{u_{i-\frac{1}{2}}}{\Delta x}-d_{is}\right)\right\}}\right\}\right ] \tag{29}\\
\end{align}
\begin{equation}
is=
\begin{cases}
i -1& u_{i-\frac{1}{2}}\geq 0の場合\\
i & u_{i-\frac{1}{2}}<0の場合
\end{cases}
\tag{30}
\end{equation}
\begin{equation}
\gamma=
\begin{cases}
1 & is =i-1 すなわちu_{i-\frac{1}{2}}\geq 0の場合\\
0 & is =i すなわちu_{i-\frac{1}{2}}<0の場合
\end{cases}
\tag{31}
\end{equation}
次に\(C_{is}=1\)の場合です。この場合、特性関数として\(\chi_{is}=1\)を用いてフラックス\(F\)を計算するのでした。式\((13)\)に\(\chi_{is}=1\)を代入し積分を計算します。
&F_{i+\frac{1}{2}}=\int_{x_{i+\frac{1}{2}}-u_{i+\frac{1}{2}}\Delta t} ^{x_{i+\frac{1}{2}}} dx\\
&\Leftrightarrow
F_{i+\frac{1}{2}}=[x]_{x_{i+\frac{1}{2}}-u_{i+\frac{1}{2}}\Delta t} ^{x_{i+\frac{1}{2}}} \\
&\Leftrightarrow
F_{i+\frac{1}{2}}=u_{i+\frac{1}{2}}\Delta t\tag{32}
\end{align}
同様に\(F_{i-\frac{1}{2}}\)は以下のように書けます。
F_{i-\frac{1}{2}}=u_{i-\frac{1}{2}}\Delta t\tag{33}
\end{align}
最後に\(C_{is}=0\)の場合です。この場合、特性関数として\(\chi_{is}=0\)を用いてフラックス\(F\)を計算するのでした。当然フラックスも0になります。
&F_{i+\frac{1}{2}}=\int_{x_{i+\frac{1}{2}}-u_{i+\frac{1}{2}}\Delta t} ^{x_{i+\frac{1}{2}}}0 dx\\
&\Leftrightarrow
F_{i+\frac{1}{2}}=0\tag{34}
\end{align}
F_{i-\frac{1}{2}}=0\tag{35}
\end{align}
以上がフラックスの求め方になります。
アルゴリズム
長くなりましたが、ようやく必要な情報が揃いました。ここまでのアルゴリズムをまとめると以下のようになります。
| (1) | 初期条件の界面状態\(C_{i}^{n}\)を与える。 |
| (2) | 式\((23)\)に基づき各セルの界面位置\(d_{i}\)を計算する。 |
| (3) | 式\((26)\sim(35)\)に基づき各セル間のフラックス\(F_{i-\frac{1}{2}},F_{i+\frac{1}{2}}\)を計算する。 |
| (4) | 式\((9)\)に基づき次ステップのVOF値\(C_{i}^{n+1}\)を求める。 |
| (5) | \(n+1→n\)とし(2)に戻る。 |
問題設定
では実際に実装してみます。下図のような速度1[m/s]で伝播するガウシアンウェーブを考えます。このような波形について、THINC法でうまく再現できるか確認します。
C(x,t)= \exp\left[{-20(x – x_{mid} – t)^2}\right]
\tag{36}
\end{align}
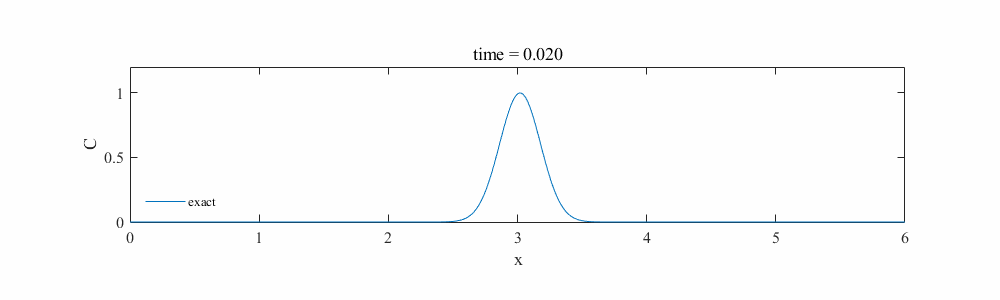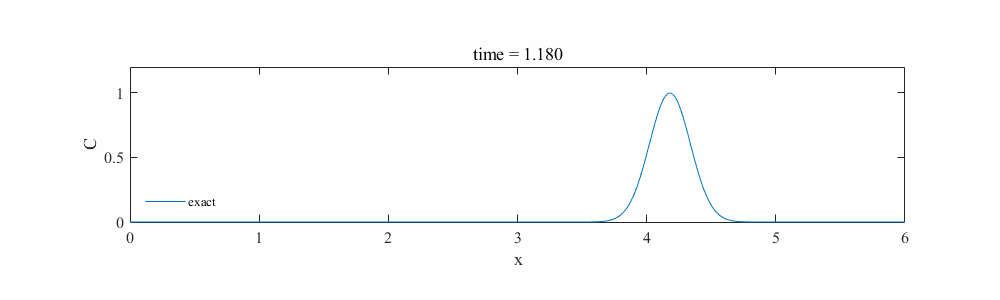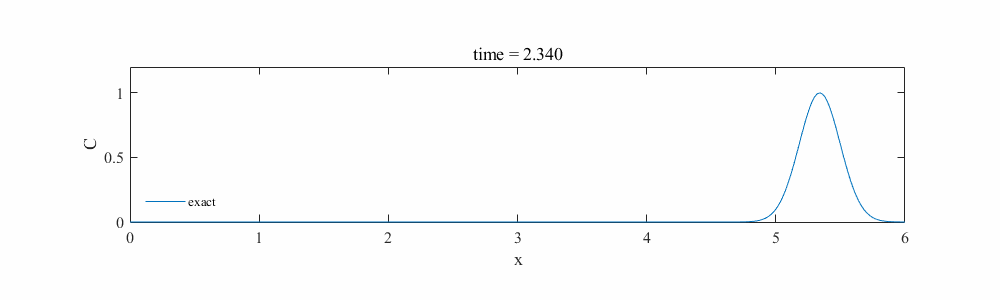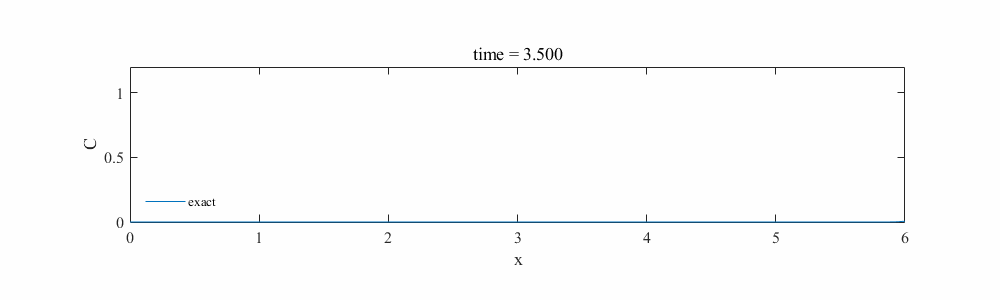
次に座標系と配列の位置関係について1*7のセル配置の例で示します。

青い領域は仮想セル領域であり、赤字で示した両端2つのセルのVOF値\(C_{1},C_{2},C_{6},C_{7}\)は境界条件として与えるものとします。これらのVOF値には以下のように壁際のセルの値をコピーしておきます。
C_1= C_2= C_3\\
C_7= C_6= C_5\\
\tag{37}
\end{align}
なぜ両端2つのセルに境界条件を課す必要があるかというと壁際のフラックス\(F_{1},F_{4}\)を求める際に必要だからです。
例えば、\(u \geq 0\)ならば、\(F_{1}\)を計算する特性関数には\(\chi_2\)を利用する必要がありました。さらに\(\chi_2\)を利用する際には界面の向き\(\alpha_2\)を決める必要があり、それは\(C_{1},C_{3}\)の大小から決まるのでした。
逆に\(u < 0\)ならば\(C_{2},C_{4}\)の情報が必要となります。したがって壁際のフラックス\(F_{1},F_{4}\)を求める際には\(C_{1},C_{2},C_{6},C_{7}\)が必要となります。
また\(C_{1},C_{2},C_{6},C_{7}\)を境界条件として与えてしまえば仮想セル領域のフラックス\(F\)は特に必要がないので設定しません。
THINC法は流速の向きによって添え字が切り替わるため実装時に配列番号を混乱しやすいです。「どの界面のフラックスを求めるのか、その界面で流速の向きはどうなってるか、参照する特性関数は左右どちらのセルのものなのか」を意識しながらプログラミングしていく必要があります。
MATLABコード
今回用いたコードは以下の通りです。githubにもアップしましたのでよろしければご参考ください。
% 初期化
clearvars;
% 座標系の生成
cor.Lx = 6;% 計算領域
cor.dLx = 0.02;% 要素サイズ
cor.x = 0 : cor.dLx : cor.Lx; % 座標の生成
cor.nx = cor.Lx / cor.dLx + 1;% 要素数
% 配列の確保
u = zeros(cor.nx, 1);
% パラメーター
pt.dt = 0.01;
pt.t_max = 3.5;
pt.iter_max = pt.t_max / pt.dt;
pt.dt_pos = 0.02;% 画像出力間隔
u(:, 1) = 1;% 移流速度
nu = u(1, 1) * pt.dt / cor.dLx;% クーラン数
beta = 0.2;
% 初期条件の設定
xmid = 0.5 * (cor.x(end) + cor.x(1));
C = exp(-20 * (cor.x - xmid).^2);% Gaussian wave
Cex = C;
Cup = C;
for iter = 1 : pt.iter_max
% 時間更新
pt.iter = iter;
pt.time = pt.iter * pt.dt;
% 厳密解
Cex = exp(-20 * (cor.x - xmid - u(1,1) * pt.time).^2);
% 1次精度風上差分法
Cup_old = Cup;
for i = 2 : cor.nx
Cup(i) = Cup_old(i) - nu * (Cup_old(i) - Cup_old(i - 1));% 1次精度風上差分
end
Cup(1) = Cup(2);
Cup(end) = Cup(end - 1);
% thinc法
C = thinc1d(C, u, beta, pt, cor);
% リアルタイム可視化
filename = ['thinc', ', beta = ', num2str(beta), ', dt = ', num2str(pt.dt), ', dx = ', num2str(cor.dLx),', u = ', num2str(u(1, 1)),', nu = ', num2str(nu(1)),'.gif'];
visplot(filename, C, Cex, Cup, beta, pt, cor,u, nu)
end
%% 以下関数
function [C] = thinc1d(C, u, beta, pt, cor)
% 配列確保
e1 = zeros(cor.nx, 1);
e3 = zeros(cor.nx, 1);
e13 = zeros(cor.nx, 1);
e4 = zeros(cor.nx, 1);
e5 = zeros(cor.nx, 1);
d = zeros(cor.nx - 3, 1);
F = zeros(cor.nx - 3, 1);
for i = 1 : cor.nx - 3 % F基準でのループ
% 流速の向きに応じて参照する特性関数の位置を切り替える。
if u(i) >= 0
is = i + 1;
gamma = 1;
else
is = i + 2 ;
gamma = 0;
end
% フラックスF_{i-1/2}をもとめる。(F_{i+1/2}ではないことに注意。)
if abs(C(is) - 1) < 10^-5 % C(is)が1ならば
F(i) = u(i) * pt.dt;
elseif C(is) < 10^-10 % C(is)が0ならば
F(i) = 0;
else
if C(is + 1) >= C(is - 1)
alpha = 1;
else
alpha = -1;
end
e1(is) = exp(beta * (2 * C(is) - 1)/alpha);
e3(is) = exp(beta);
e13(is) = e3(is)*(e3(is)-e1(is))/(e3(is) * e1(is)-1);
d(is) = 0.5 / beta * log(e13(is));
e4(is) = cosh(beta * (gamma - u(i) * pt.dt / cor.dLx - d(is)));
e5(is) = cosh(beta * (gamma - d(is)));
F(i) = 0.5 * (u(i) * pt.dt + alpha * cor.dLx / beta * log(e5(is) / e4(is)));
end
end
% 移流方程式を解く
for i = 3 : cor.nx - 2% C基準でのループ
Cf = (F(i - 1) - F(i - 2)) / cor.dLx;% セルiから抜け出るVOF値
C(i) = C(i) - Cf;% 流速の湧き出し項は無視する
end
% 境界条件
C(1) = C(3);
C(2) = C(3);
C(end - 1) = C(end - 2);
C(end) = C(end - 2);
% 可視化
% コマンドウィンドウへの出力
txt = ['iter = ', num2str(pt.iter), ' / ', num2str(pt.iter_max)];
disp(txt);
end
function [] = visplot(filename, C, Cex, Cup, beta, pt, cor,u, nu)
%plot(cor.x, Cex, cor.x, C)
plot(cor.x, Cup, cor.x, C)
% 軸の設定
title(['time = ', num2str(pt.time, '%.3f')]);
set(gca, 'FontName', 'Times New Roman', 'FontSize', 12);
axis equal;
%axis tight; axis on;
fig=gcf;
fig.Position = [100 100 1000 300];
fig.Color='white';
xlim([cor.x(1) cor.x(end)]);
ylim([0 1.2]);
xlabel('x')
ylabel('C')
% 凡例
%legtxt = ['thinc', ', beta = ', num2str(beta), ', dt = ', num2str(pt.dt), ', dx = ', num2str(cor.dLx),', u = ', num2str(u(1, 1)),', nu = ', num2str(nu(1))];
%legend({'exact', legtxt},'Location','southwest','FontSize', 10)
legtxt = ['1st order upwind', ', dt = ', num2str(pt.dt), ', dx = ', num2str(cor.dLx),', u = ', num2str(u(1, 1)),', nu = ', num2str(nu(1))];
legtxt2 = ['thinc', ', beta = ', num2str(beta), ', dt = ', num2str(pt.dt), ', dx = ', num2str(cor.dLx),', u = ', num2str(u(1, 1)),', nu = ', num2str(nu(1))];
legend({legtxt, legtxt2},'Location','southwest','FontSize', 10)
legend('boxoff')
frame = getframe(1);
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if pt.time == pt.dt_pos
imwrite(imind, cm, filename, 'gif', 'DelayTime', 0.1, 'Loopcount', inf);
elseif rem(pt.time, pt.dt_pos) == 0
imwrite(imind, cm, filename, 'gif', 'DelayTime', 0.1, 'WriteMode', 'append');
end
end
計算結果
まず、1次精度風上差分法と結果を比較してみましょう。以下に\(dt = 0.01, dx = 0.02, nu = 0.5\)の計算結果を示します。
風上差分法は数値粘性により波形が減衰していくのに対し、THINC法は数値粘性の影響が皆無です。如何にTHINC法の界面保存特性が優れているかが分かります。また上記はクーラン数0.5の例ですが、クーラン数が1を超えると両者ともに発散するようです。
次に界面の厚みパラメーターである\(\beta\)を変更し、厳密解と比較してみます。
\(\beta=0.2\)の結果は比較的厳密解と一致していますが、\(\beta\)が増加するほど数値解は矩形波に近づいていき、厳密解と形が異なっていくことが分かります。\(\beta\)の大きさによって特性関数の形状が変化し、フラックスに誤差が生じることでこのような変化が起こっているものと思われます。
どうやらTHINC法は\(\beta\)を適切に設定することが重要のようです。数値粘性の影響はないものの、波形を歪めるのは問題ですね。この辺がどれぐらいクリティカルな問題になるのかは現段階で作者には分かりませんが、おそらくこの辺もよく研究されてるのでしょう。
おわりに
今回は1次元のTHINC法を実装し、厳密解、風上差分法と比較を行いました。THINC法は特性関数のtanh関数を使うため、VOF値のように輸送量が0~1の間にある時のみに利用可能な手法であり、通常のナビエ・ストークス方程式には利用できません。しかしながら、その界面保存特性は既存手法と比較しても大変優れていると思います。一方で実際的な流れ場において適切な界面厚みパラメーターを選定するのはかなり難しいようにも思います。
今回は1次元系で述べましたが、原著論文では多次元への拡張、自由表面解析への適用が述べられており、手法自体も今まさに発展途上と思われます(学会などでもTHINC法関連の報告がちらほらみられる)。今後気が向けばそのへんも記事にしていければと思います。しかし今回の記事はちょっと長くなりすぎたかな…。まあいいか…。
参考文献
[1] F. Xiao, Y Honma and T. kono, “A simple algebraic interface capturing scheme using
hyperbolic tangent function“, Int. J. Numer. Meth. Fluid. 48, 1023 (2005).
[2] W. Aniszewski, T. Menard, M. Marek Erratum to: “Volume of Fluid (VOF) type advection methods in two-phase flow: A comparative study”. Computers & Fluids, Volume 152, 18 July 2017, Pages 193-194
[3] Yokoi. K, “Efficient implementation of THINC scheme: a simple and practical smoothed VOF algorithm”, Journal of Computational Physics 226 (2) (2007) 1985-2002.
[4] 中西 為雄, “ヘビサイド関数の解析多重積分に基づく新しい界面捕獲法“, 第32回数値流体力学シンポジウム(2018)
[5] @implicit_none, “自由表面流れにおける代数的界面再構成法と,その計算過程で現れる不適切な結果を物理的観察で回避する方法”, Qiita, 2019年12月08日, https://qiita.com/implicit_none/items/7230b1ab9b8b71d58b13
[6] 肖 鋒, “数値流体解析の基礎- Visual C++とgnuplotによる圧縮性・非圧縮性流体解析 -“, コロナ社, 2020




コメント